边界流形嵌入在特征提取中的应用

龚思聪，徐 洁，万鸣华

1.广东工业大学 自动化学院，广州 510006

2.南京审计大学 信息工程学院，南京 211815

降维是计算机视觉、模式识别、机器学习等领域[1-3]常见的数据分析和处理方法。在人脸识别[4-5]、数据可视化等领域[6-9]，通常需要从高维数据中提取有效的低维特征，以方便数据分析和处理。用于降维的特征提取算法不仅可以减少计算机的存储空间和计算成本，还可以去除数据的冗余信息，提取数据的本质特征[10-11]。降维算法主要包括线性降维算法和非线性降维算法。线性降维算法最典型的包括：主成分分析（principal component analysis，PCA）[12-14]和线性判别分析（linear discriminant analysis，LDA）[15-16]。PCA是一种无监督的降维算法，其核心思想是找到一组正交基，将高维数据映射到低维空间，使降维后的数据方差最大，从而达到尽可能多地保留原始高维数据的信息。LDA是一种监督的降维算法，其目标是寻找一组最优投影向量来最大化类间散度矩阵和类内散度矩阵之间的比值，使得同一类数据尽可能聚集在一起，不同类数据尽可能分开。

但是这两种算法都旨在保留原始高维数据的全局欧氏结构，并不能挖掘到原始高维数据的局部流形特征。因此，众多基于流形学习的非线性降维算法被广泛研究，如：等距映射（isometric mapping，ISOMAP）[17-18]、局部线性嵌入（locally linear embedding，LLE）[19-20]、拉普拉斯特征映射（Laplacian eigenmaps，LE）[21-22]等。这些非线性流形学习降维算法，通过高维空间样本点之间的近邻关系来刻画原始高维数据的局部流形特征，并且使数据降维后依然保留这种局部流形特征。然而这些非线性流形学习算法不仅计算成本高，而且仅仅定义在训练样本集上，对于一个新的测试样本，无法给出高维数据到低维数据的映射关系。为了解决这个问题，基于相似性保留的线性化流形学习方法被提出。典型的算法有：邻域保持嵌入（neighborhood preserving embedding，NPE）[23-24]和局部保留投影（locality preserving projection，LPP）[25-26]，此类算法都通过线性嵌入来保留数据的局部流形特征，给出了高维数据到低维数据的映射关系，但仅通过保留原始高维数据的局部流形特征，并不能很好地表征原始高维数据的可分性[27]。于是，基于图嵌入的降维算法——边界Fisher分析（marginal Fisher analysis，MFA）[28-29]、局部敏感判别分析（locality sensitive discriminant analysis，LSDA）[30-31]、判别最大化边界投影（discriminant maximum margin projections，DMMP）[32]相继被提出。DMMP算法在保留原始高维数据局部流形特征的同时，最大化不同类样本之间的边界，然而，DMMP算法使用的类间权重不随样本之间的距离而改变，不能很好地反映出样本在高维空间的边界信息。MFA算法和LSDA算法利用数据的局部结构为每个样本点构造本征图和惩罚图，使得同一类的样本点投影后相互靠近，不同类的样本点投影后相互远离。MFA算法分别寻找每个样本点的同类近邻点和异类近邻点，来构造本征图和惩罚图，这容易导致样本点所选择的同类近邻点和异类近邻点之间没有必然的联系。与MFA算法相比，LSDA算法首先给定每个样本点的近邻域半径，然后根据近邻点的标签信息将邻域里的近邻点分为同类近邻点和异类近邻点，进而构造出本征图和惩罚图。对于LSDA算法来说，由于未考虑样本点的分布情况，容易导致样本点的近邻域里只有同类样本点，离群点的近邻域里只有异类样本点，从而无法找到划分同类样本点和异类样本点之间的边界，这大大地削弱了LSDA算法在分类任务中的性能。为了减弱LSDA算法的离群点问题，提升的局部敏感判别分析（improved locality sensitive discriminant analysis，ILSDA）[33]和局部敏感判别投影（locality sensitive discriminant projection，LSDP）[34]相继被提出。ILSDA算法在LSDA算法的基础上引入样本的全局结构，通过最小化类内散度来减弱离群点问题。LSDP算法在最小化同类近邻样本投影后距离的同时，为了使同类样本投影后具有更强的紧密程度，最小化同类非近邻样本投影后的距离来减弱离群点问题。然而，这两种算法仍然面临为样本点构造近邻域的时候，容易导致样本点的近邻域里只有同类样本点的问题。

为了更有效地利用样本点的边界信息，更好地解决MFA算法和LSDA算法所面临的问题，本文提出了一种新的图嵌入降维算法——边界流形嵌入（marginal manifold embedding，MME）。MME算法利用样本点的标签信息，首先寻找到距离每个样本点的最近异类边界子流形（邻域），再返回本类中寻找距离异类边界子流形最近的同类边界子流形（邻域）。这样一来，MME算法可以为每个样本点寻找到位于边界的紧密联系的同类边界子流形和异类边界子流形，从而定义出同类样本点和异类样本点之间的边界。受Fisher鉴别准则启发，MME算法在保留同类样本点边界局部邻域结构的同时，最大化每个样本点的同类边界子流形和异类边界子流形之间的距离，从而得到具有鉴别意义的低维特征空间。另外，值得一提的是，MME算法很好地将徘徊在边界的离群点收入到边界邻域里，这在一定程度上能够减弱离群点给算法带来的负面影响，实验也验证了MME算法的有效性。

1 相关算法

X=[x1,x2,…,xN]∈RD×N，X为给定N个样本点所组成矩阵，其中每一个样本xi∈RD为一个D维列向量。每个样本xi所属的类别记作l(xi)，共有c类样本，即l(xi)∈{1,2,…,c}，第i类样本点的个数为ni，样本点总个数为定义线性投影矩阵A∈RD×d，经过线性变换yi=ATxi，可将原始空间中的D维数据xi转换为d维数据yi∈Rd，其中d≪D。

1.1 边界Fisher分析（MFA）

在MFA算法中，定义了类内权重矩阵和类间权重矩阵，分别建立两个邻接图：本征图和惩罚图。在本征图中，对于每一个样本点xi，定义类内权重矩阵Ww，如果xj属于xi同类的k个近邻样本点，那么Wijw=Wjiw=1，否则Wijw=Wjiw=0；在惩罚图中，对于每一个样本xi，定义类间权重矩阵Wb，如果xj属于xi异类的k个近邻样本点，那么Wijb=Wjib=1，否则Wijb=Wjib=0。MFA算法通过边界Fisher准则寻找最佳投影方向：

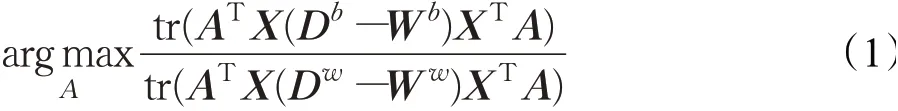
1.2 邻域保持嵌入（NPE）

假设在高维空间中一共有n个样本点，NPE算法中，每一个样本点xi可以被它的k个最近邻样本点线性重构。首先构造邻接图，对于每一个样本点xi，如果样本点xj属于其k个近邻样本点，那么从xi到xj生成一条有向边。定义权重矩阵W，如果从xi到xj存在有向边，则存在权值Wij，否则为零。W可以通过求解如下最小化问题获得：

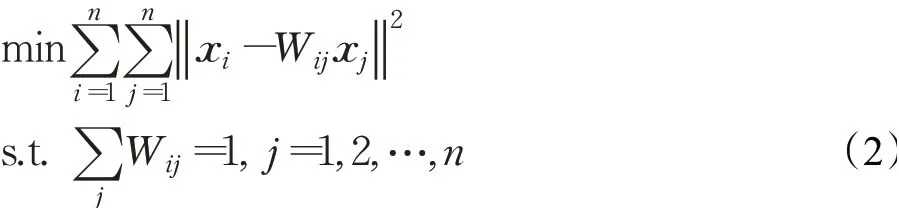
NPE算法认为高维空间中样本点的重构关系同样会在低维空间中保持，因此线性投影矩阵A=可以通过求解以下最小化问题获得：

其中，M=(I-W)T(I-W)，I为单位矩阵。

利用拉格朗日算子，将式（3）优化问题转换为：

线性投影矩阵A=[a1,a2,…,ad]由式（4）中最小的d个特征值所对应的特征向量构成。

2 边界流形嵌入（MME）

2.1 算法基本思想

MME算法根据样本点的标签信息，首先寻找距离每个样本点最近的异类边界子流形，再返回本类中寻找距离此异类边界子流形最近的同类边界子流形。这样一来，每个样本点都关联着一对匹配的边界子流形。在获得有针对性的边界后，MME算法利用同类边界子流形的样本点构造本征图，目的在于更好地保持同类样本点边界流形的局部邻域结构。但同时为了更好地实现分类，MME算法利用异类边界子流形的样本点构造惩罚图，目的在于增大同类样本点和异类样本点之间的距离。MME的目的很明确，样本点嵌入到低维空间后，不仅能够保留同类样本点的局部边界邻域结构，还能获得更好的鉴别性能。

2.2 寻找边界

如图1所示，表示一个三分类问题。三类样本点分别用不同的形状表示。以第1类中的样本点xi为例，计算样本点xi与第2类和第3类所有样本点的欧氏距离，取距离xi最近的k1个样本点，构成样本点xi的异类近边界邻域集合。计算的均值mb，再计算mb与样本点xi所在类别（即：第1类）的其他样本点的欧氏距离，取距离mb最近的k2个样本点，构成样本点xi的k2个同类边界邻域集合从图1可以看出构成的异类边界邻域集合和构成的同类边界邻域集合是密切联系的，通过减小样本点xi与内样本点之间的距离，同时增大样本点xi与内样本点之间的距离，能够有效将第1类样本点与第2类、第3类样本点分开。

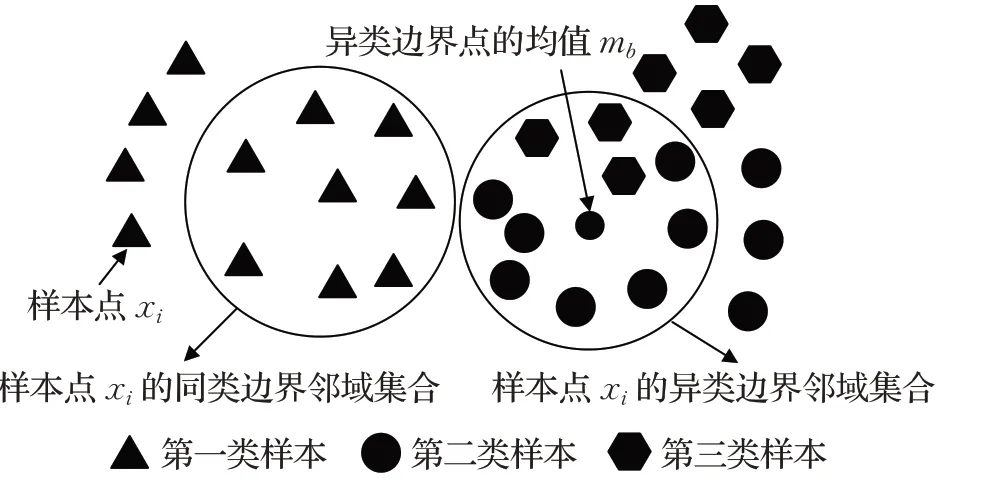
图1 MME算法寻找边界样本点的示意图Fig.1 Diagrammatic sketch of finding marginal samples by MME algorithm

2.3 目标函数

对于类内权值矩阵Ww通过求解式（5）获得：

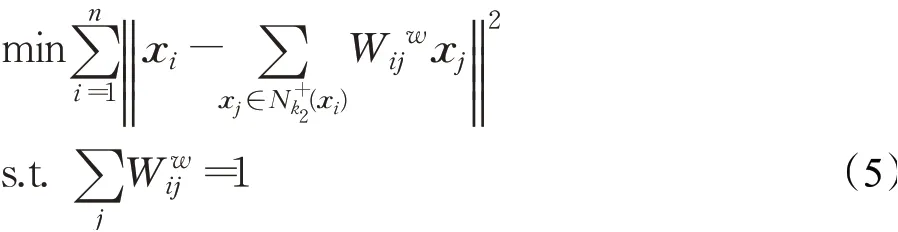
对于类间权值矩阵Wb通过求解式（6）获得：

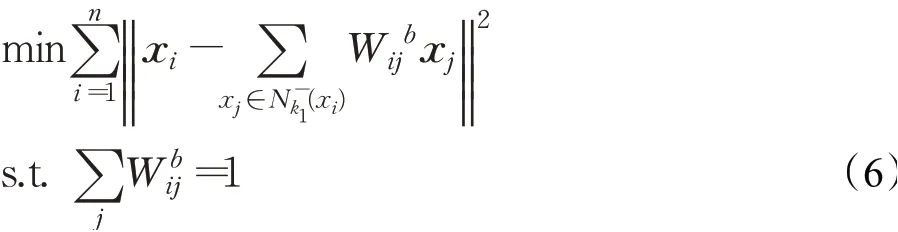
给定一线性投影矩阵A，训练样本集X通过线性投影矩阵A嵌入到低维空间后，类内的重构误差为：

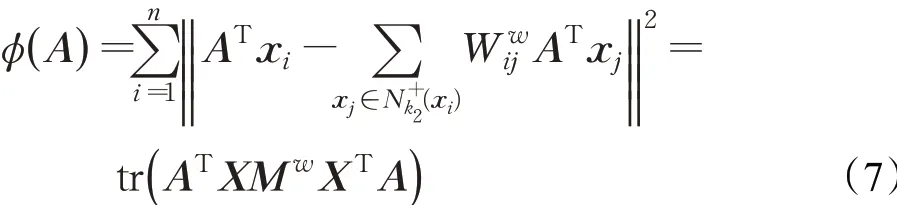
训练样本集X通过投影矩阵A嵌入到低维空间后，类间的重构误差为：

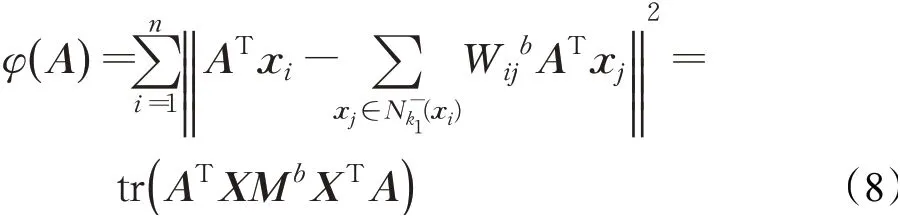
为了获得更好判别性能的低维数据，需要最大化类间重构误差，最小化类内重构误差，那么进一步可重新表述为：

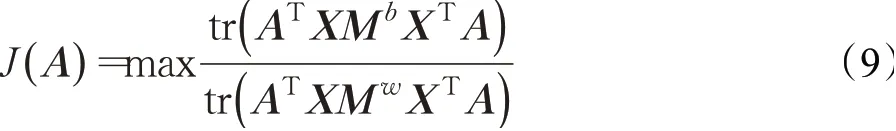
利用拉格朗日算子可将上式的优化问题转化为：

A=[a1,a2,…,ad]由式（10）中最大的d个特征值所对应的特征向量构成。

2.4 算法步骤

输入已知训练集样本矩阵X=[x1,x2,…,xn]∈RD×N，与样本点对应的标签l=[c1,c2,…,cn]∈R1×N，测试集样本xj∈RD×1，样本点的约简维数d，训练样本点的异类近邻点个数k1，训练样本点的同类近邻点个数k2。

输出最佳线性投影矩阵A∈RD×d，训练样本集矩阵X的低维表示Y∈Rd×N，和测试集样本xj的低维表示yj∈Rd×1。

（1）计算训练集每个样本点xi∈RD×1和异类样本点的欧氏距离，取距离xi最近k1个样本点构成集合，再计算的均值mb。

（2）计算mb与样本点xi所在类别的其他样本点的欧氏距离，取距离mb最近的k2个样本点构成集合

（3）通过式（5）和式（6）计算类内权值矩阵Ww和类间权值矩阵Wb。

（4）求解式（10）d个最大特征值对应的特征向量，构成投影矩阵A∈RD×d。

（5）计算Y=ATX得到训练集样本降维后的结果Y∈Rd×N，计算yj=ATxj，得到测试集样本xj的降维结果yj∈Rd×1。

2.5 LSDA、MFA、MME算法边界的比较

MFA算法分别寻找每个样本点xi的k1个同类最近邻样本点，k2个异类最近邻样本点，构造本征图和惩罚图，k2个异类样本点构成了样本点xi的异类边界点。如图2所示，有两类样本点，分别用不同的形状表示。以第一类样本中的样本点xi为例，当k1和k2都取2时，样本点xi所选择的同类近邻样本点和异类边界样本点之间没有必然联系。减小样本点xi与同类近邻样本点之间的距离，同时增大样本点xi与异类边界样本点之间的距离并不能很好地表征同类样本点和异类样本点之间的可分性。

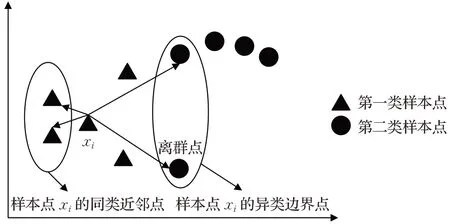
图2 MFA算法的边界点分析图Fig.2 Marginal samples analysis graph of MFA algorithm

LSDA算法首先寻找每个样本点的k个最近邻样本点，然后根据最近邻样本点的标签信息将每个样本点的k个最近邻样本点划分为同类邻域和异类邻域，进而形成边界，为保护样本点的局部线性特征，k值选择不能过大。如图3所示，当k值取4时，第一类样本点中的样本点xi只有同类近邻点，而没有异类近邻点，从而无法为样本点xi构造惩罚图。对于离群点来说，也容易遇到近邻域里只有异类近邻点的情况，从而无法为离群点构造本征图。这两种情况都会削弱LSDA算法在分类任务中的性能。

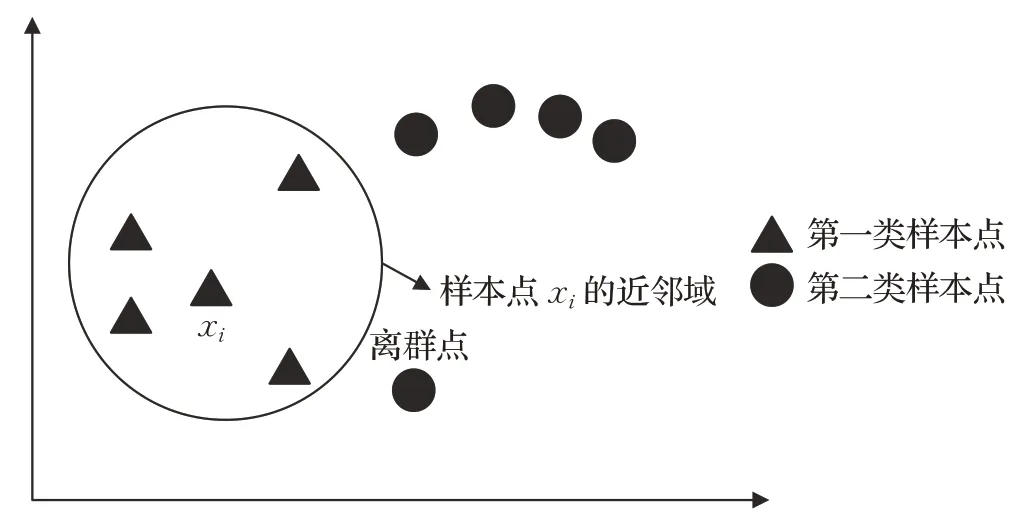
图3 LSDA算法的边界点分析图Fig.3 Marginal samples analysis graph of LSDA algorithms

本文中提出的MME算法，充分地利用了边界样本点的信息，并且能够减弱离群点给算法带来的负面影响。如图4所示，以第一类样本中的样本点xi为例，首先寻找距离xi最近的2个异类边界点构成样本点xi的异类边界子流形，异类边界点的均值mb能够反映异类边界点的分布情况，于是计算距离mb最近的2个第一类样本点，构成样本点xi的同类边界子流形。这样一来，通过样本点xi形成的同类边界子流形和异类边界子流形有着紧密的联系，通过最大化样本点xi与异类边界子流形的距离，同时最小化样本点xi与同类边界子流形的距离，能够有效地将第一类样本点与第二类样本点分开。同时，可以注意到离群点通常位于样本点的边界，MME算法在为每个样本点构造同类边界邻域和异类边界邻域的时候，很容易将离群点收入到边界邻域内，这在一定程度上能够减弱离群点给算法带来的负面影响。

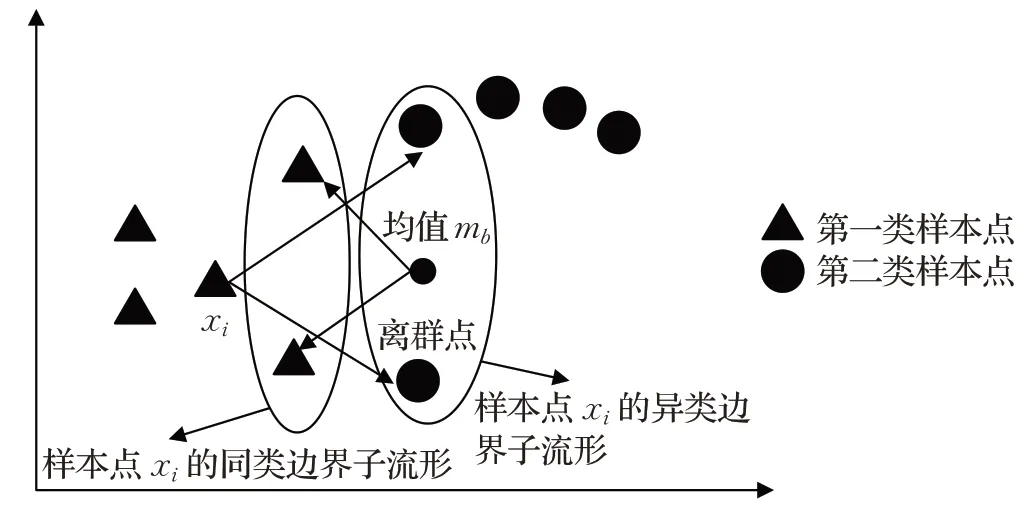
图4 MME算法的边界点分析图Fig.4 Marginal samples analysis graph of MME algorithm

3 实验仿真

在本文实验中，采用MATLAB R2014b来实现各种算法，所用计算机内存为8 GB，CPU为Intel®Core™i5-4200H CPU@2.80 GHz，主频为2.80 GHz。为了验证MME算法的有效性，在ORL、PIE、YaleB人脸数据库上进行实验，与使用全局几何结构的PCA、LDA算法、局部结构的流形学习算法LSDA、MFA、NPE、DMMP、ILSDA、LSDP算法对比。NPE算法中选取每个样本点的其他同类样本点构造邻接图。实验中先用PCA算法对训练集样本进行预处理，保留99%的能量，以去除冗余信息，同时可以避免LDA、MFA、LSDA、NPE、LSDP、DMMP、MME算法的小样本问题，再在训练集上求投影矩阵A，再对所有训练样本和测试样本进行降维处理，最后用基于欧氏距离的最近邻分类器对降维后的测试集数据进行分类，得出准确率。MME、LSDA、MFA、NPE、DMMP、ILSDA、LSDP算法涉及到参数选择问题，本文经过详细的超参数搜索工作，使各个算法分类的准确率达到最大，来获取最优参数。

3.1 ORL人脸库实验

ORL数据集包括40个不同人的共400幅图像，每人共有10幅图像，包括面部表情、光照方向、面部朝向的方向、睁眼或者闭眼、是否戴眼镜等多种变化。对ORL数据集的图像进行裁剪和缩放得到尺寸为32×32像素的灰度图像，部分图像如图5所示。

图5 ORL人脸库两个人各10幅图像Fig.5 Two persons in ORL face database，10 images per person

实验中，在ORL人脸数据库中，在每类样本中随机取p=2,3,4,5个样本作为训练集，剩余样本为测试集，对于固定的p值，进行20次随机实验，其均值作为算法最终的识别率。Baseline方法即为数据没有降维直接采用最近邻分类器分类。LDA算法的最大降维维度为c-1，c为ORL人脸数据库类别数量。表1展示了各个算法最优平均识别率的均值以及最优平均识别率均值的标准差。图6展示了4种划分情况下，ORL人脸数据库平均识别准确率与投影维度变化曲线图。

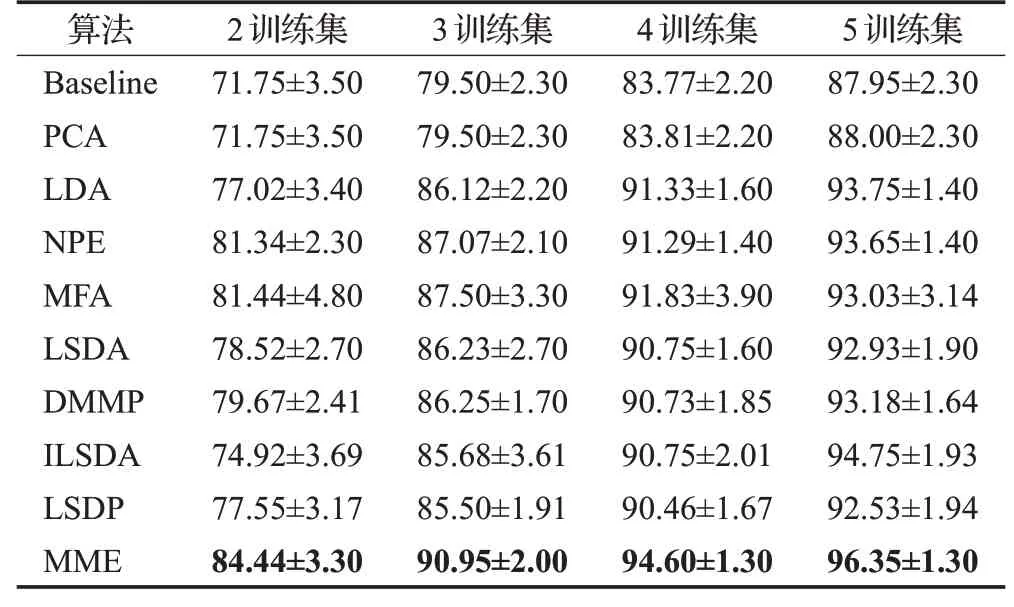
表1 各算法在ORL数据集的最优平均识别率对比（均值±标准差）Table 1 Top average classification accuracy and corresponding standard deviation on ORL database单位：%

由表1和图6可知，随着样本训练集的增加，各个算法的平均识别率都有显著提升，无监督的PCA算法在所有的算法中识别率最低，相对于Baseline方法基本没有提升，这表明在分类任务中样本的标签信息非常重要。MME算法的平均识别率在各个投影维度变化下均高于其余算法，在投影维度为1至40维时，MME算法的平均识别率提升显著，并明显优于其他降维算法，这表明MME算法所提取的低维特征能够获得很好地表征不同类样本点的可分性。同时，当投影维度大于40维到70维时，随着投影维度的增加，NPE、MFA、LSDA、ILSDA、LSDP算法识别率出现一定程度下滑，而MME算法在此情况下，平均识别率仍能很好地保持在最优值附近，说明随着维度的增加，MME算法所提取的低维特征能够更有效地保留数据的判别信息和表征数据的本质结构，所保持的样本点的局部边界信息相比于MFA算法和LSDA算法能够更好地表征同类样本点和异类样本点的可分性。随着训练样本数的增加，MME算法比较于LDA、NPE、DMMP算法的识别率也明显要高很多，这表明样本点的密切联系的局部边界信息对于分类具有重要意义。

图6 ORL数据集平均识别准确率与投影维度变化曲线图Fig.6 Average classification accuracy versus projection vectors number on ORL database

3.2 PIE人脸库实验

PIE人脸数据库包含68位志愿者的41 368张多姿态、光照和表情的面部图像，其中的姿态和光照变化图像是在严格控制的条件下采集，每幅图片大小为92×112像素。实验中，采用PIE人脸库正面姿势（C09）在不同的光照和表情下68个人的所有图像，每个人24幅图片，总计1 632张图片进行实验，所有图像根据眼睛坐标进行旋转、剪切、缩放到64×64像素的图片，部分人脸图像如图7所示。

图7 PIE人脸库中两个人的部分图像Fig.7 Partial image of two people in PIE face database

实验中，在PIE人脸数据库中，在每类样本中随机取p=6,8,10,12个样本作为训练集，剩余样本为测试集，对于固定的p值，进行10次随机实验，其均值作为算法最终的识别率。表2展示了各个算法最优平均识别率的均值以及最优平均识别率均值的标准差。图8展示了4种划分情况下，PIE人脸数据库平均识别准确率与投影维度变化曲线图。

由表2和图8可知，随着训练样本的增加，各个算法的平均识别率都有一定的提升，相对于有监督的降维算法，无监督的PCA算法在所有的算法中识别率最低，这与ORL库的实验结论一致。在所有的监督性降维算法中，保持数据点局部结构的MFA、LSDA、NPE、DMMP、ILSDA、LSDP、MME算法与仅保持数据全局结构的LDA算法相比，识别率更高，这在一定程度上表明了维持样本局部流形特征对于分类的重要性。同时，随着训练样本数增加，ILSDA算法和LSDP算法在为样本点构造近邻域的时候，容易导致其近邻域里只有同类近邻点，导致ILSDA算法和LSDP算法相比于LSDA算法，识别率提升不明显，甚至没有提升。同时，也可以注意到利用边界局部信息的LSDA算法、MFA算法相比于只利用同类样本点局部信息的NPE算法，识别率差别不大，这除了与数据集本身没有体现出不同算法之间的差异性有关之外，也从一定程度上表明了LSDA算法和MFA算法所保留的边界局部信息在一些情况下并不能很好地表征同类样本点和异类样本点的可分性。与之相比，MME算法投影维度较低的情况下，最优平均识别率能够优于其他降维算法，而且随着训练样本数的增加，训练集包含更多的信息，MME算法的识别率上升得较快，优于其他降维算法，这表明MME算法为每个样本点寻找紧密相联的同类边界子流形和异类边界子流形构造本征图和惩罚图，所保留的边界局部信息相比于MFA、LSDA、DMMP、ILSDA、LSDP算法能够更好地表征同类数据点和异类数据点的可分性。

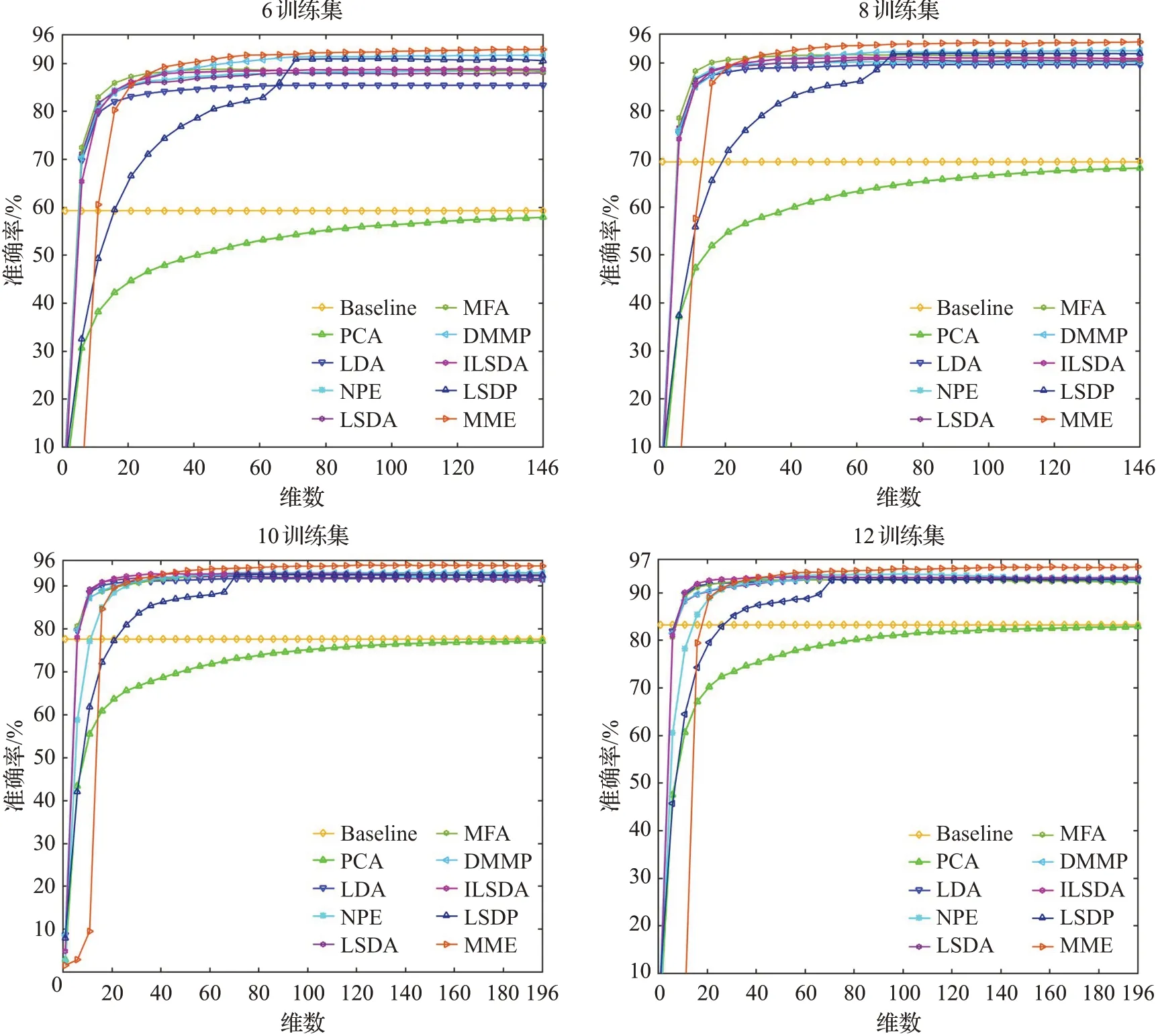
图8 PIE数据集平均识别准确率与投影维度变化曲线图Fig.8 Average classification accuracy versus projection vectors number on PIE database

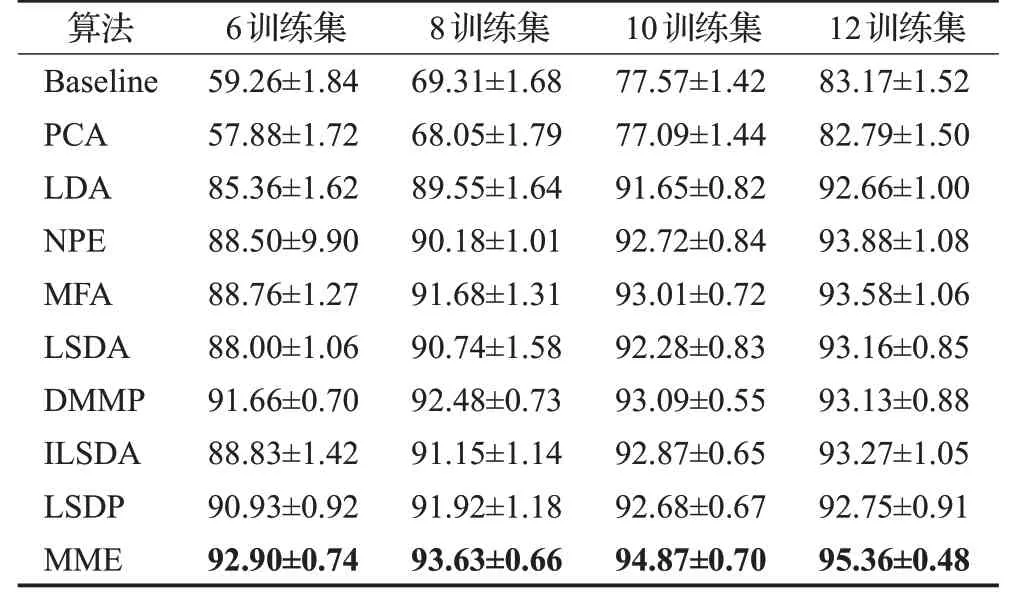
表2 各算法在PIE数据集中的最优平均识别率对比（均值±标准差）Table 2 Top average classification accuracy and corresponding standard deviation on PIE database单位：%

3.3 YaleB人脸库实验

Extend YaleB人脸数据库包含38个人，每个人9种姿态有64种光照条件，共有图像16 128幅图像。在实验中，选取Extend YaleB人脸库在不同光照条件下38个人的正面姿势图像，每人64幅图像，总计2 432张图片进行实验，所有图像根据眼睛坐标进行旋转、剪切、缩放到32×32像素的图片，部分图像如图9所示。

图9 YaleB人脸库中两个人的部分图像Fig.9 Partial image of two people in YaleB face database

实验中，在YaleB人脸数据库中，在每类样本中随机取p=5,10,20,30个样本作为训练集，剩余样本为测试集，对于固定的p值，进行10次随机实验，其均值作为算法最终的识别率。表3展示了各个算法最优平均识别率的均值以及标准差。图10展示了四种划分情况下，YaleB数据集的准确率与投影维度的变化曲线图。

通过表3和图10可见，随着训练样本集增加，ILSDA算法相对于LSDA算法的识别率提升不明显，这在一定程度上反映了ILSDA算法使用了类内样本的全局结构，不利于样本之间局部流形特征的维持，这削弱了算法在分类任务中的性能。而LSDP算法在最小化同类近邻样本的投影距离的同时，最小化同类非近邻样本的投影距离，一定程度上减弱了离群点给算法带来的影响，相比于LSDA算法收获了明显更高的识别率。与之相比，MME算法在投影维度较高情况下最优平均识别率能够较明显优于其余算法，而且随着训练样本的增加，训练集包含更多的信息，所有算法的最优平均识别率都有较明显提高，但MME算法的最优平均识别率上升更为明显，使得MME算法在投影维度不断增加的情况下，与其他算法相比，平均识别率的优势也越大。这表明MME算法提取的低维特征能够很好地表征原始高维数据的可分性，所保留的边界结构信息相比于LSDA、MFA、DMMP、ILSDA、LSDP算法能够更好地揭示原始高维数据的判别结构。同时，在不同的训练样本下，当MME算法的识别率达到最大之后，随着投影维度的增加，MME算法的识别率能够很好地稳定在最优值附近，这也说明了MME算法具有一定的鲁棒性。

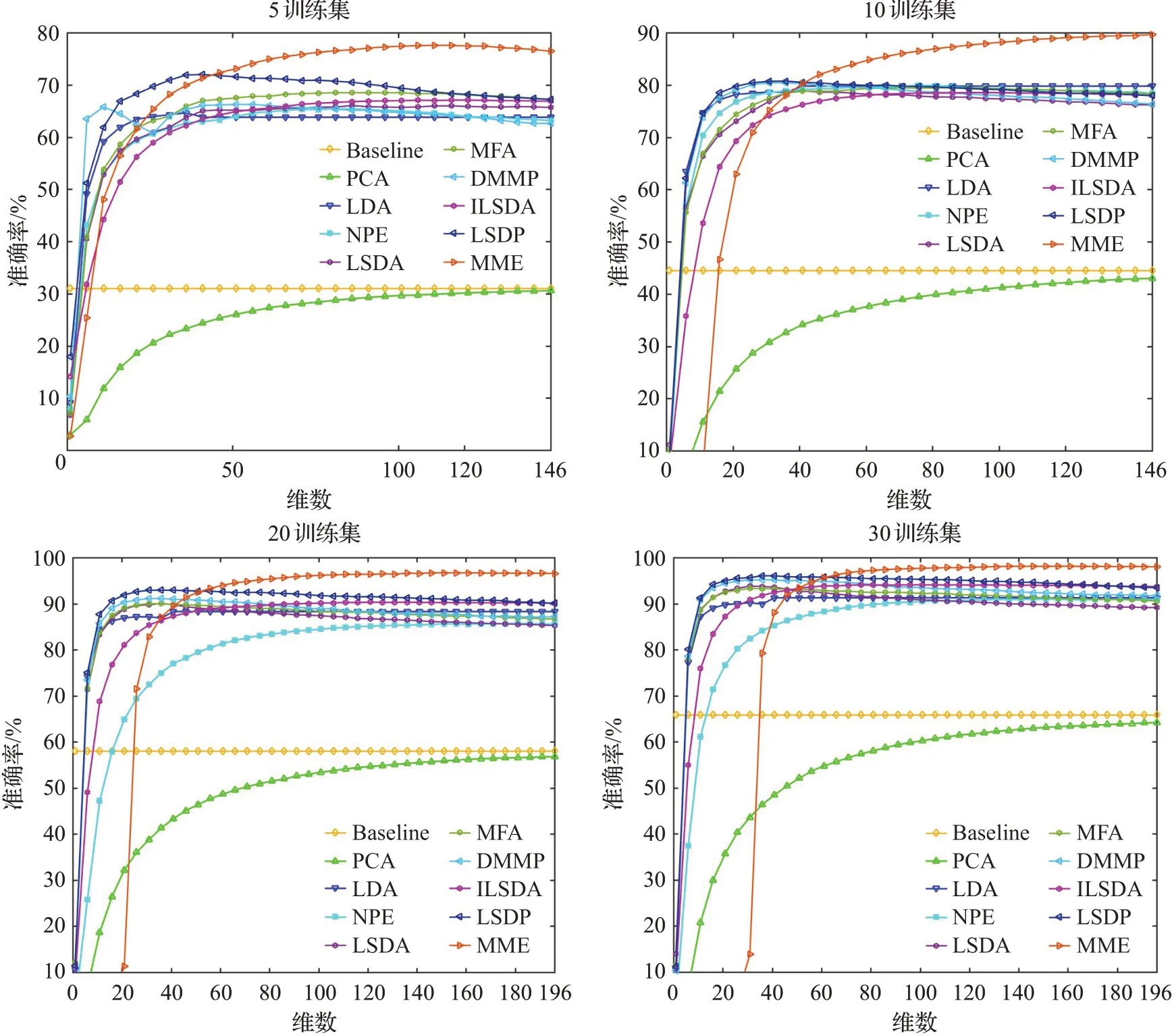
图10 YaleB数据集平均识别准确率与投影维度变化曲线图Fig.10 Average classification accuracy versus projection vectors number on YaleB database

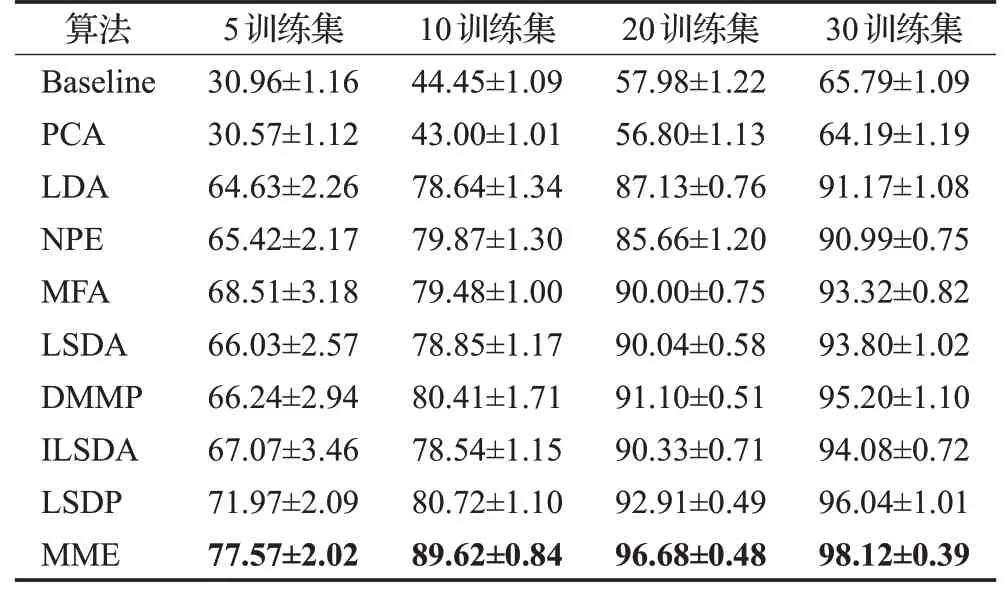
表3 各算法在YaleB数据集中的最优平均识别率对比（均值±标准差）Table 3 Top average classification accuracy and corresponding standard deviation on YaleB database单位：%

4 结束语

本文提出了一种新的图嵌入降维算法——边界流形嵌入（MME），MME算法充分利用了样本点的边界信息，通过为每个样本点寻找紧密联系的同类边界子流形和异类边界子流形，使得每个样本点构造本征图和惩罚图所选择的同类边界点和异类边界点能够很好地表征不同类样本点的可分性。因此，MME算法将数据降维之后，能够获得较好的鉴别性能。在ORL数据集、PIE数据集、YaleB数据集的实验及分析表明了MME算法在多种情况下能够取得较好的分类效果，适合分类任务。

虽然MME算法获得了良好的改进效果，但算法仍有可改进的地方，由于MME算法需要人工选择两个参数，在实际应用中会产生参数选择的困难。如何自适应确定参数值是未来需要进一步研究的问题。