改进黑猩猩优化算法的测试数据生成研究
高大唤,梁宏涛,杜军威,于 旭,胡 强
青岛科技大学 信息科学技术学院,山东 青岛 266100
随着软件规模、需求及复杂度的不断提升,软件缺陷率不断增长[1-2],而发现软件缺陷的唯一途径就是对软件进行测试。软件测试作为软件工程生命周期中的关键阶段之一,其中测试数据纵贯软件测试的全部流程。软件测试的主要目标是生成有效的测试数据,而如何在有限的时间内生成有效的测试数据是软件测试领域的研究难点之一[3],在有限的时间内选择一组代码覆盖率较高的输入数据是自动化测试数据生成技术的主要目标[4]。在软件测试技术的探索中,出现了众多测试数据生成方法,基于启发式的生成算法成为当下学者的研究主流,并被广泛应用到测试数据[5-9]。
启发式优化算法在测试数据生成中的应用可追溯到1976年,当时美国研究人员Miller和Spooner[10]试图在浮点测试数据生成中使用搜索算法,但是他们没有继续相关的工作;Khan等[11]将遗传算法和变异分析方法进行融合用于测试数据自动生成,但只有运行变体,才能得到这个变体的分数,这就导致运行时间有所增加;何海鲜等[12]提出将布谷鸟改进算法用于测试数据自动生成,证明效果优于其他算法,但是在降低冗余数据的生成效果方面并不明显;Sahoo和Ray等[13]在测试数据生成中使用改进组合适应度函数的粒子群算法可有效提高路径覆盖数量,但未考虑到覆盖多个关键路径的测试数据生成效率;Mahdieh等[14]提出将故障倾向性估计纳入测试数据的优先级排序中可提高测试数据的生成及优先级排序效率,不足的是未考虑开发过程历史中的测试用例执行结果;何庆等[15]提出了在黑猩猩优化算法中融合多策略,提高了算法的收敛速度,并在机械设计中得到很好的运用和效果,算法虽整体性能提高得不少,但其收敛速度相对过快。
虽上述文献对各种启发式优化算法进行改进,在一定程度上能改善算法的寻优精度和收敛效果[16-18],进而提高测试数据的生成效率,但目前测试数据生成大多集中在启发式搜索算法的某些单一算法上,如遗传算法、蚁群算法等,这种算法有一些先天的局限,如过早收敛、搜索精度不足、容易陷入局部最优解等[19-20]。另外,在测试数据生成方面对于新型的算法研究相对较少。黑猩猩优化算法[21](chimp optimization algorithm,ChOA)是2020年由Khishe等提出的一种新型算法。它不仅具有流程简单、参数少、能与各种优化问题结合的优点,还具有两大主要特点:一是将种群划分为一个个独立的个体,可以有效提高算法的勘探能力;二是引入混沌因子,有助于改善开发过程的收敛速度和精度[22]。不足是ChOA算法也存在易陷入局部最优和收敛过早等问题。因此,本文提出一种正余弦扰动策略黑猩猩优化算法,先使用拉丁超立方策略初始化种群,增加群体多样化;其次引入非线性衰减收敛因子来平衡全局和局部开发能力;然后在位置更新时添加正余弦扰动因子,防止算法发生停滞现象;另外考虑到该算法目前尚未在测试数据生成领域中得到应用,因此考虑将其应用到测试数据的自动生成中;最后通过实验对比验证算法有效性及在测试数据生成中的生成效率和可行性[23]。
1 黑猩猩优化算法
ChOA是由Khishe于2020年提出的一种较为新颖的启发式搜索算法,它的原理是仿照黑猩猩的社会行为进行狩猎进而达到寻优的目的,分为四类黑猩猩[24],即,攻击黑猩猩(attacker)、驱逐黑猩猩(driver)、阻碍黑猩猩(barrier)和追赶黑猩猩(chaser),四类黑猩猩中攻击黑猩猩是领导者,其他三类配合领导者进行打猎。下面是黑猩猩在驱逐和追赶猎物过程的数学模型:
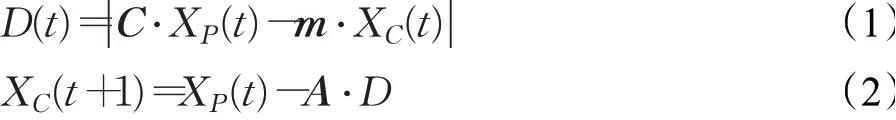
其中,t为当前迭代次数,D是黑猩猩与猎物间的距离,XP为猎物的位置,XC为黑猩猩的位置,A、C、m均为系数矢量,且A是决定黑猩猩与猎物距离的系数矢量,C是控制黑猩猩驱逐和追赶猎物的系数矢量,m表示社会激励对黑猩猩个体位置的影响,A、C、m的表达式为:

其中,R1、R2属于[0,1]区间内的随机值,f为线性递减因子。
四种黑猩猩的位置更新公式如下:
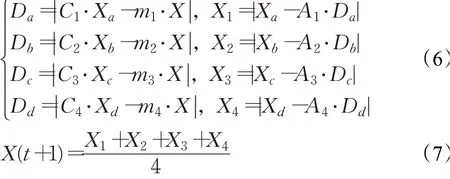
其中,X为当前黑猩猩的位置,Xa、Xb、Xc和Xd分别表示攻击黑猩猩、阻碍黑猩猩、驱逐黑猩猩及追赶黑猩猩的位置,X(t+1)表示更新后t+1代黑猩猩的位置,C1、C2、C3和C4均为随机分别在[0,1]区间的数。
在狩猎过程黑猩猩位置更新的数学模型如下:
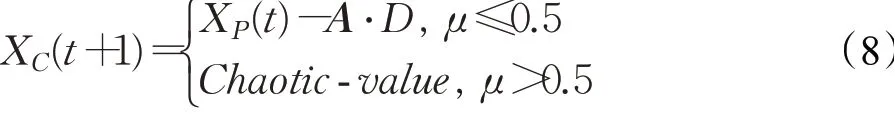
其中,μ是随机分布在[0,1]区间内的数,Chaotic-value为混沌因子。
2 改进黑猩猩优化算法
目前,在基本的ChOA中,使用随机分布的方式初始化种群,这种方式导致种群的多样性降低;其次,算法使用线性收敛因子来平衡全局和局部开发能力,会导致算法寻优速度迟缓;最后,原始算法存在易陷入局部极值现象。因此,针对基础算法存在的局限,提出多种改进策略,具体介绍如下。
2.1 拉丁超立方策略初始化种群
很多原始的启发式优化算法均采用随机方式初始化种群,随机分布具有随机性、不确定性,这种方式会导致种群分布不均及算法搜索能力下降,但是群体优化算法又依赖于群体的初始化位置。而混沌状态是自然界普遍存在的一种非线性现象,具有遍历性、不重复性和对初始值敏感性的特点,很多学者根据这些特点将其应用于到算法优化问题。目前大多数文献常用的混沌映射是Logistic映射,但是Logistic映射存在中间分布均匀、两端分布密集的问题。针对上述存在的问题,本文提出采用拉丁超立方初始化种群,由于它具有均匀分层的特征,可以均匀遍布整个空间,覆盖率更高,能以较小的采样规模获得较高的采样精度,因此,LHS映射比随机方式和Logistic映射分布较为均匀,用来初始化种群的效果更佳,三种方法的对比效果如图1所示。
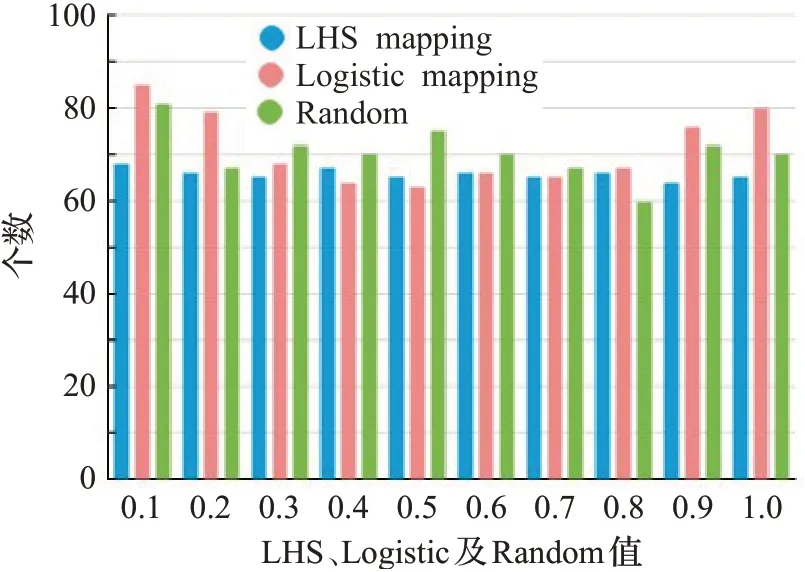
图1 LHS、Logistic及随机方式的频率分布直方图Fig.1 Frequency distribution histogram of LHS,Logistic and Random
设全局搜索范围[UB,LB],初始种群规模为N,每维xi变量的定义域区间划分为N个相等的小区间,数学模型如下:

设搜索空间是二维空间,拉丁超立方初始化种群如图2(a)和(b)所示。
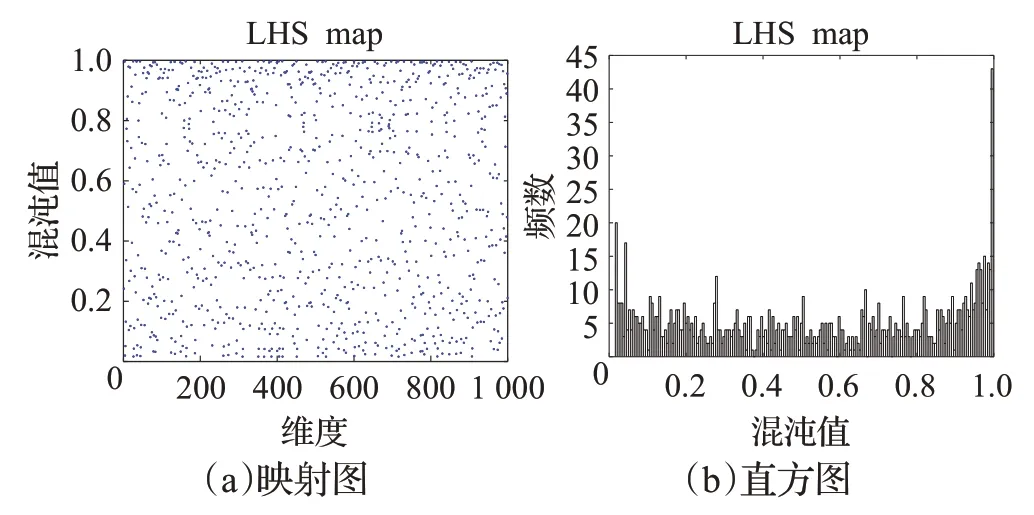
图2 拉丁超立方初始化种群分布映射和直方图Fig.2 Latin hypercube initialization population distribution map and histogram
由图2可知,拉丁超立方初始化种群可使种群分布得更加均匀,覆盖率更加广泛,因此,采用拉丁超立方进行初始化种群可以提高种群的多样化和种群的质量。
2.2 非线性衰减收敛因子
动态变化的衰减收敛因子种类繁多,如:线性衰减收敛因子、高斯衰减收敛因子、对数衰减收敛因子、指数衰减收敛因子等,在标准的ChOA中,一般采用线性递减因子来控制算法的全局和局部开采能力,但是这种方式并不能较好地权衡算法的全局和局部勘察能力,导致算法搜索速度迟缓,图3是5种收敛因子对比曲线图。
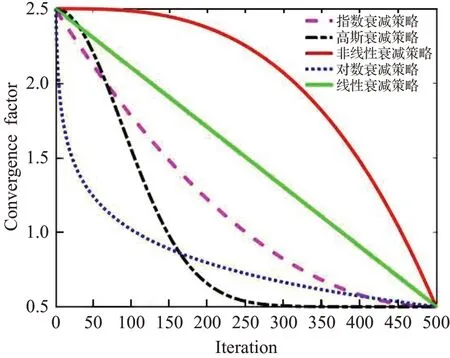
图3 收敛因子曲线图Fig.3 Convergence factor graph
图3中可以看出,在5种递减策略中,虽然不同策略在不同程度上都可以平衡算法的探索和开发能力,但是如果在寻优初期收敛因子衰减过快,会使算法全局探索能力变弱,存在易陷入局部极值的问题,所以非线性立方衰减策略更具优势,因此,本文提出一种非线性立方衰减收敛因子。在算法迭代初期先扩大算法的搜索空间进行大范围的全局开采,提高算法的寻优效果,在此过程中收敛因子逐渐下降,算法开始收缩搜索范围进行小范围的局部开发,局部勘察有助于算法在短时间内找到最优值。非线性立方衰减收敛因子的数学模型为:

其中,t当前迭代数,Tm为最大迭代数,f"为非线性衰减收敛因子。
标准ChOA算法中的线性收敛因子呈线性衰减,而本文提出的非线性立方衰减因子呈非线性衰减,这种方法不仅增大了算法的搜索范围,提高了算法的全局开拓能力,也有利于算法的局部开采,提高算法的寻优精度,避免算法陷入局部极值,缩短算法的寻求最优值的时间成本。
2.3 正余弦扰动因子
在标准的ChOA算法中,黑猩猩位置更新主要靠每次迭代进行更新,通过计算适应度值,选择其中最优的作为攻击者黑猩猩,攻击黑猩猩是四类黑猩猩的领导者,其位置更新的好坏直接决定了整体算法寻优的效率和准确度,但是这种对攻击者黑猩猩的强依赖性不利于算法的寻优。当陷入局部范围搜索时,其周围将聚集大量其他黑猩猩,进而会导致算法陷入局部最优,无法探索搜索空间中的新区域。为了避免这种现象,本文提出将正余弦波信号进行改进后的正余弦波因子融入到黑猩猩位置更新过程,引入该因子可使算法跳出局部范围,提高算法的寻优能力,使其避免坠入局部最优,其迭代100次的图形如图4所示。
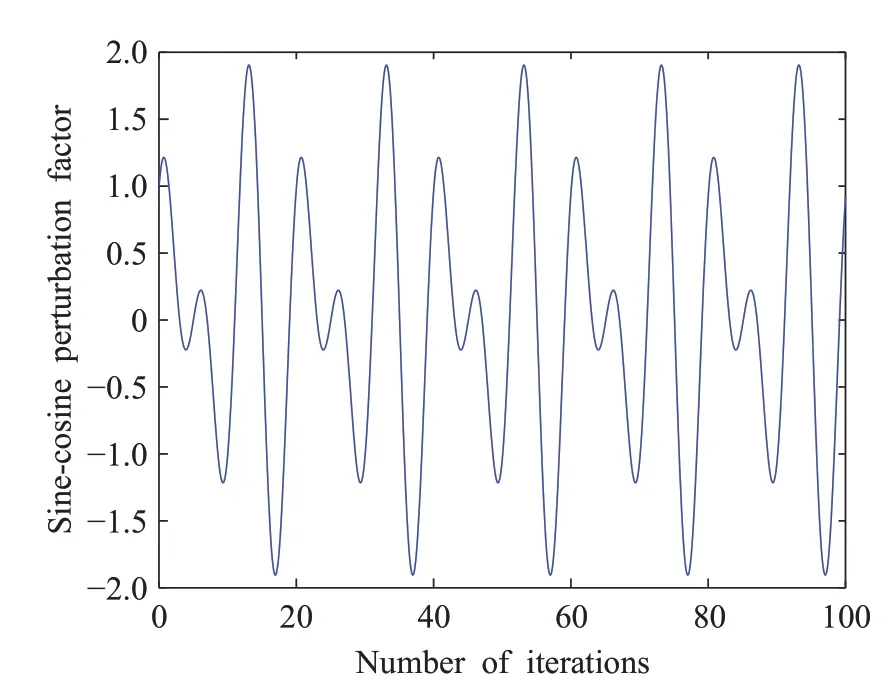
图4 正余弦扰动因子分布Fig.4 Sine and cosine perturbation factor distribution
利用正余弦扰动因子动态变化的不确定性对四类黑猩猩在位置更新时进行不同程度的扰动,使得四类黑猩猩能向更广泛的区域进行搜索,扩大了算法的搜索规模,降低了其他黑猩猩盲目跟随攻击者黑猩猩的概率,提高了算法跳出局部极值的能力。
正余弦扰动因子的数学模型公式如下:
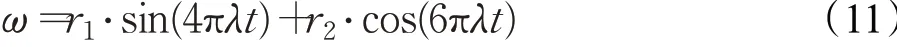
其中,r1、r2属于[0,1]区间内的随机值,λ是控制参数。
在标准ChOA中引入正余弦扰动因子后的四类黑猩猩的位置更新公式为:
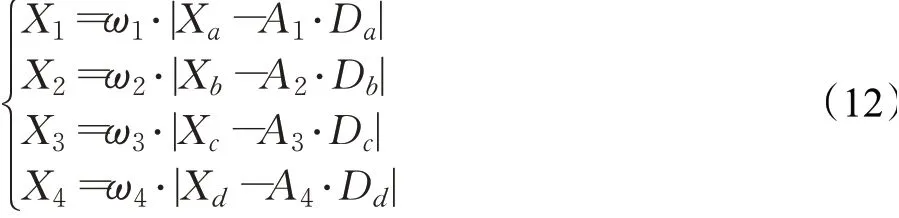
2.4 算法实现流程
综合上述改进策略,本文提出的正余弦扰动策略黑猩猩优化算法(SC-ChOA),它是在标准的ChOA基础上进行的改进,引入三个策略,其一使用拉丁超立方初始化种群,其二将ChOA的线性收敛因子改进为非线性衰减收敛因子,其三对标准ChOA主要依赖攻击黑猩猩的特点进行改进,使用正余弦扰动因子对四类黑猩猩位置进行扰动。SC-ChOA算法的输入为拉丁超立方初始化种群及相关参数,输出为最优黑猩猩个体的位置,具体实现步骤及伪代码如下:
步骤1初始化种群规模,最大迭代次数Tm、搜索范围UB、LB,并设置相应参数。
步骤2采用LHS初始化种群Xi,i=1,2,…,N。
步骤3计算每个个体的适应度值,找出最优的前四个值记为四种黑猩猩个体,分别记为Xa、Xb、Xc和Xd。
步骤4根据公式更新系数向量A、C及非线性衰减收敛因子的值f"。
步骤5通过正余弦扰动因子进一步更新四类黑猩猩的位置及其他黑猩猩的位置。
步骤6判断是否达到最大迭代次数,若无,则跳转到步骤3,否则结束算法,并输出最优黑猩猩的位置Xa。
SC-ChOA算法流程如图5所示。
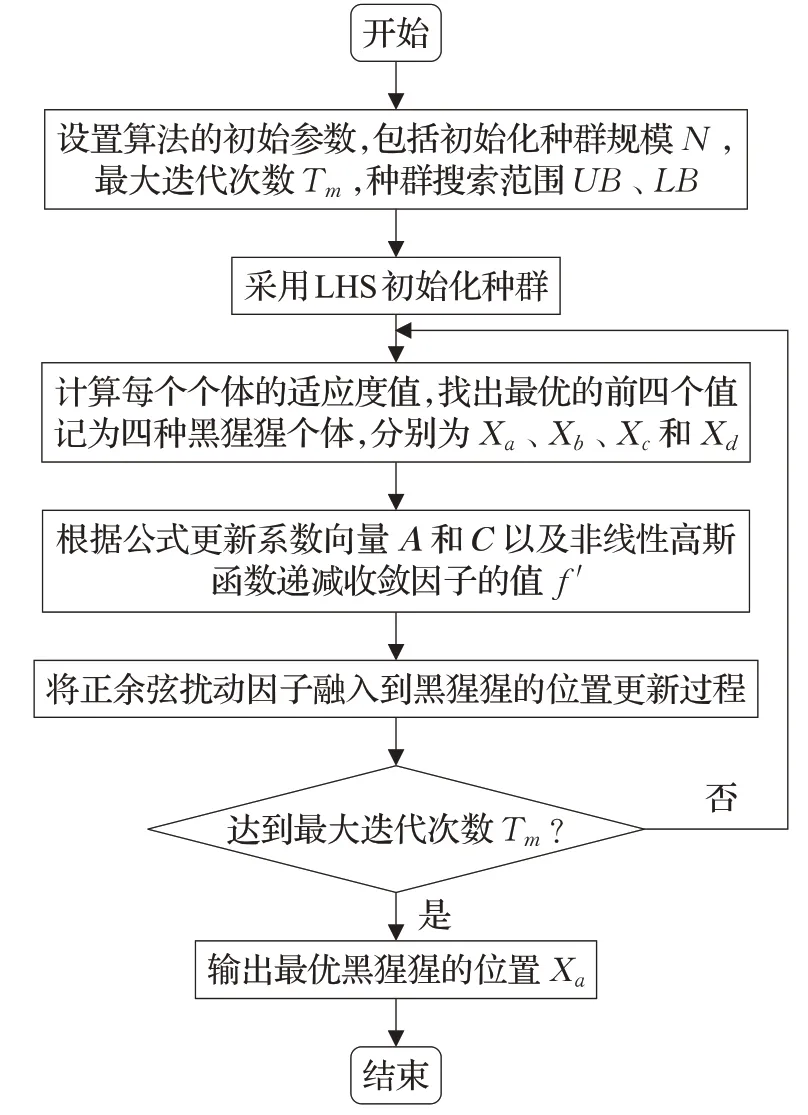
图5 SC-ChOA算法流程图Fig.5 SC-ChOA algorithm flowchart
2.5 时间复杂度分析
算法的时间复杂度是关于输入规模n的函数,可直接反映算法的收敛速度,用来检验算法运行效率的关键指标,在标准ChOA算法中,假设种群规模N,搜索空间维度n,参数初始化时间为t1,随机初始化种群的时间为t2,则标准ChOA初始化阶段的时间复杂度为:

设计算种群个体适应度值所需时间为f(n),选择前四个最优值个体位置的时间为t3,更新线性衰减收敛因子的时间为t4,根据前四个最优个体更新种群其他黑猩猩个体位置所需时间为t5,则标准ChOA迭代寻优阶段的时间复杂度为:
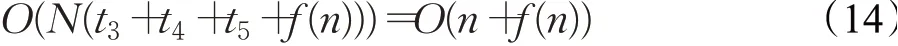
因此,标准的ChOA算法迭代寻优过程总的时间复杂度为:
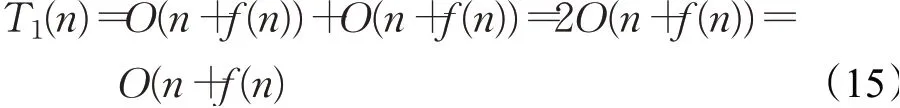
在SC-ChOA算法中,初始化相关参数所需时间与标准ChOA相同,采用拉丁超立方策略初始化种群所需时间为t6,在算法迭代阶段非线性衰减收敛因子递减时间为t7,执行正余弦扰动因子的时间为t8,更新四类黑猩猩位置所需时间为t9,则SC-ChOA算法的时间复杂度为:
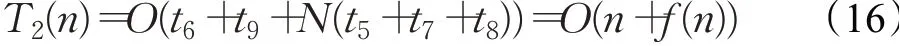
根据相关文献研究表明,遗传算法(genetic algorithm,GA)的时间复杂度为:

综上所述,SC-ChOA算法和标准ChOA算法的时间复杂度属于同一数量级别,对算法改进并没有增加算法的时间复杂度,且均小于GA算法的时间复杂度,即:

3 实验仿真与结果分析
3.1 实验设计与测试函数
实验设备:Windows 10操作系统,计算机处理器3.30 GHz,内存16 GB,算法使用MATLAB R2016a编写。为了评价SC-ChOA算法的实际效果,与标准的ChOA[25]及常用的GA[26]进行实验对比,选择10个不同特征的测试函数,其中f1~f5为单峰值函数;f6~f8为多峰值函数;f9~f10为固定维度多峰函数,如表1所示。
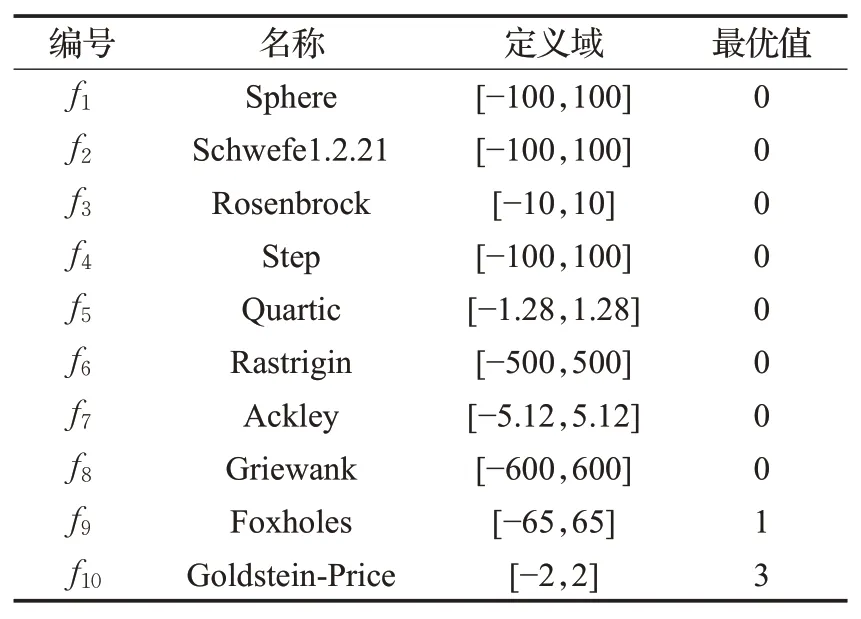
表1 测试函数Table 1 Test function
3.2 算法寻优性能分析
为了证明改进算法SC-ChOA的有效性及其动态收敛性,将本文加入的拉丁超立方初始化、非线性衰减收敛因子及正余弦扰动因子三个策略的SC-ChOA算法与标准ChOA算法及GA算法在10个不同特性的测试函数上进行实验对比。
为确保实验公平性,取空间维度d=30,最大迭代次数Tm=100,群体规模N=30,每个函数运行30次,取最优值、平均值、标准差及算法的运行时间四个性能指标来评价每个算法的寻优效果,最优值和平均值可以用来反映算法的寻优效果和收敛速度,标准差可以反映算法的稳定性和鲁棒性,运行时间对应算法的收敛速度,运行时间越少,说明算法收敛速度越快,反之亦然,具体对比结果如表2所示。
通过表2的最优值和平均值可直接反映出算法的寻优效果和收敛速度的能力。首先,从最优值的结果可以看出,SC-ChOA在求解单峰函数f2、f4及多峰函数f6时均取得了最优值0,在求解两个固定维度多峰函数f9和f10时,也取得了最优值1和3。在求解多峰值函数f7的最优值时,因为f7是山谷形状的,其全局最优值位于山谷最低端,很难取到最优值,但是SC-ChOA和ChOA的平均寻优精度可达到10-80以上,而GA的平均寻优精度只能达到10-70以上,另外,SC-ChOA相比于ChOA和GA在达到寻优精度的基础上,其运行时间也比标准ChOA和GA的运行时间少,这说明SC-ChOA在求解最优值时不论单峰函数、多峰函数还是固定维度的多峰函数,SC-ChOA算法都具有良好的稳定性和鲁棒性。其次,从平均值的结果可以看出,标准ChOA求解函数最优值的寻优能力有限,而SC-ChOA在f2、f4和f6均获得了最优解,这是因为在标准ChOA中引入了正余弦扰动因子对函数局部最优解进行了扰动,使其向全局最优解靠拢,提高了算法的寻优精度和收敛速度。在求解f5和f7时,SC-ChOA和ChOA的寻优精度达到级别相近,均可直接收敛到最优解附近,但是SC-ChOA相比于ChOA的运行时间少很多,提高了收敛速度,这是因为在标准ChOA中引入了非线性立方衰减收敛因子,有效平衡了算法的全局和局部搜索能力,加快算法收敛速度,缩短算法的寻求最优值的时间成本。对于形状类似于抛物面存在大量的局部极值的函数f1、f2、f3和f8,仅有改进的SC-ChOA取得了最优值,而标准ChOA和GA均未取得最优解,这说明在标准ChOA中引入三个策略得到的SC-ChOA算法更有助于求解具有大量局部极值的函数。综上所述,无论在寻优精度还是稳定性上,融入三种策略的SC-ChOA均表现出一定的优势。
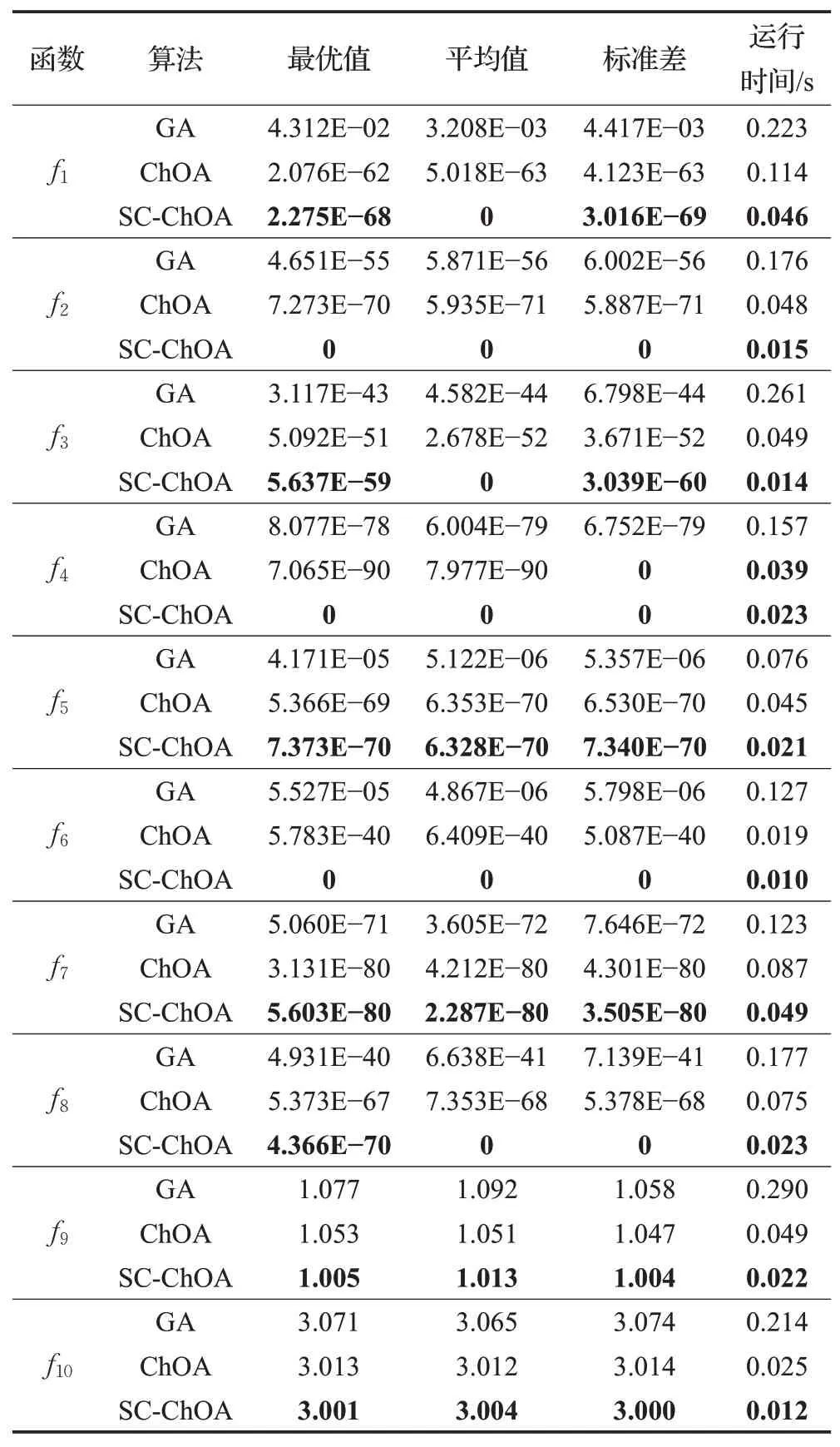
表2 10个测试函数实验结果Table 2 Experimental results of 10 test functions
3.3 算法收敛性分析
为了更加直观地反映三种算法在求解不同特征测试函数f1~f10的寻优精度和动态收敛性,图6给出了三种算法在10个测试函数的收敛曲线图。
由图6可以看出,对于10个测试函数,SC-ChOA在算法迭代初期的收敛曲线下降速度较快,在迭代末期的开拓性能也优于其他两个算法,且在整个寻优迭代过程,SC-ChOA的收敛曲线均在ChOA和GA下面,这表明引入的拉丁超立方初始化种群和非线性衰减收敛因子策略不仅能保证算法的全局开拓能力和种群的多样性,也有效提高了算法的收敛速度。图6(a)~(e)是单峰函数的收敛曲线图,从图中可以看出,ChOA算法的收敛曲线在迭代初期T=30附近,均出现陷入算法停滞的现象,而改进算法SC-ChOA在迭代初期可以快速下降,且在整个迭代过程没有出现明显的陷入算法停滞的状态,这表明融入的正余弦扰动因子策略能带领群体找到全局最优值,有助于群体跳出局部极值,进而有效地改进了标准ChOA算法存在的易陷入局部极值的问题,并且加入了非线性立方衰减收敛因子可有效平衡算法的全局和局部勘察能力;图6(f)~(h)是多峰函数的收敛曲线图,从图中可以发现SC-ChOA的收敛曲线在整个迭代过程可快速下降,并取到最优解,虽然在算法迭代初期ChOA的收敛曲线也可以快速下降,但其存在算法停滞现象,如f8在迭代次数T=40次后,算法没能跳出局部极值完全进入了停滞状态,导致算法最终未取到最优解。而GA均为未取到最优值,且SC-ChOA和ChOA的寻优精度均比GA提高了至少50个数量级,这说明新型黑猩猩优化算法的寻优效果明显优于传统的遗传算法。对于函数f6、f7,虽然SC-ChOA和ChOA都能达到寻优精度,但是SC-ChOA达到寻优精度时所用的迭代次数明显小于ChOA,如对于f6,SC-ChOA找到最优值时所用的迭代次数大约为50次,而ChOA找到最优值时所用的迭代次数大约为70次;对于f7,SC-ChOA找到最优值时所用的迭代次数大约为30次,而ChOA找到最优值时所用的迭代次数大约为50次,这进一步说明了引入正余弦扰动因子和非线性衰减收敛因子策略的SC-ChOA可以提高算法的收敛速度,减少算法找到最优解时所消耗的迭代次数。图6(i)、(j)是固定维度的多峰函数的收敛曲线图,从图中可以看出,三种算法均可达到寻优精度,且SC-ChOA和ChOA的收敛曲线下降速度高于GA,另外,对于f9,SC-ChOA和ChOA找到最优值时所用的迭代次数大约分别为35次、80次;对于f10,SC-ChOA和ChOA找到最优值时所用的迭代次数大约分别为60次、90次,这明显可以看出融入三种策略的SC-ChOA相比于标准ChOA在算法整个寻优过程中的收敛速度有很大程度的提高,且SC-ChOA和ChOA均优于GA。
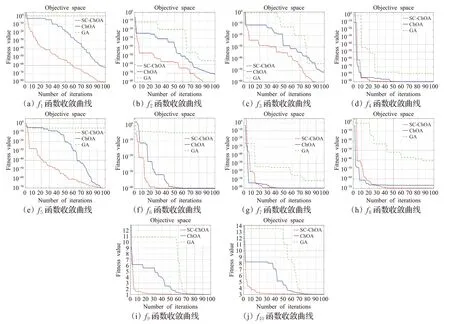
图6 三种算法收敛对比图Fig.6 Convergence comparison chart of three algorithms
综上所述,表2的实验结果与图6的收敛曲线验证了本文所提改进算法的有效性。SC-ChOA均达到了寻优精度,且收敛速度也是相对较快的,虽然ChOA在某些测试函数上未取到最优值,但是其收敛速度优于GA算法。因此,对于单峰函数、多峰函数及固定维度的多峰函数,无论在寻优精度上,还是收敛速度上,SCChOA相比于ChOA和GA均具有较好的寻优性能和收敛速度。
4 SC-ChOA测试数据生成应用与分析
测试数据生成问题是软件测试领域普遍关注的重要问题,测试数据的生成效率直接决定了软件测试的整体效率。在软件测试技术的探索中,出现了众多测试数据生成方法,其中,基于启发式优化算法成为当下学者的研究主流,其思想是将测试数据生成问题通过适应度函数转化为一个函数最优化问题,然后利用启发式优化算法进行求解。本文为验证改进算法SC-ChOA在解决实际问题中的有效性,将其应用于测试数据生成中,下面进行详细的介绍。
4.1 测试数据生成模型框架
测试数据生成模型主要包括3个模块:
(1)静态分析模块
通过对测试程序的分析,得到程序控制流程图,从中选择测试程序的目标路径,并得到算法的部分参数。同时,根据流程图得到测试主程序的插桩程序。
(2)测试驱动模块
该模块主要负责建立适应度函数,在测试运行的过程中,输入为算法返回的测试数据集,使用这些测试数据集驱动被测程序。并且通过适应度函数评价测试用例,返回适应度值给算法部分。
(3)算法生成测试数据模块
该模块是测试数据自动生成的重要模块。算法完成初始化任务后,将初始数据输入到测试驱动模块,对测试驱动模块传来的适应度值进行检查,判断当前运行结果是否是最优解或迭代次数达到最大,若符合条件,算法终止,输出最优的测试数据,否则继续迭代,直到找到最优解。改进启发式搜索算法的测试生成模型框架如图7所示。
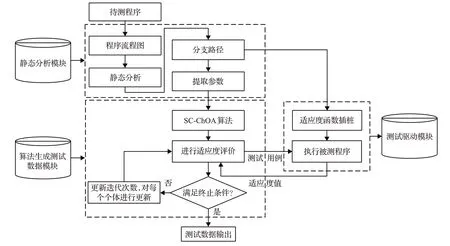
图7 基于SC-ChOA算法的测试数据生成模型框架Fig.7 Test data generation model framework based on SC-ChOA algorithm
4.2 程序插桩技术与适应度函数构造
4.2.1 程序插桩技术
程序插桩技术是由Gallagher提出的,思想是在每个语句分支中插入适当函数获取执行时的信息,来评价测试数据。被测程序的测试技术是由Huang最先发明的,在程序结构中添加代码来收集程序执行信息,并用以记录在驱动程序工作过程中测试结果的内在活动和关键特性[27]。
测试数据自动生成系统的主要实现方式是基于测试程序中的桩插入,其基本思路为:
(1)首先对数据进行随机初始化;
(2)判断单个驱动程序执行路径与目标路径的偏差;
(3)最后采用逐步迭代的方法生成测试数据。
为了更好地解释程序插桩法,以三角形类型判断为例进行插桩,三角形决策流程图如图8所示。
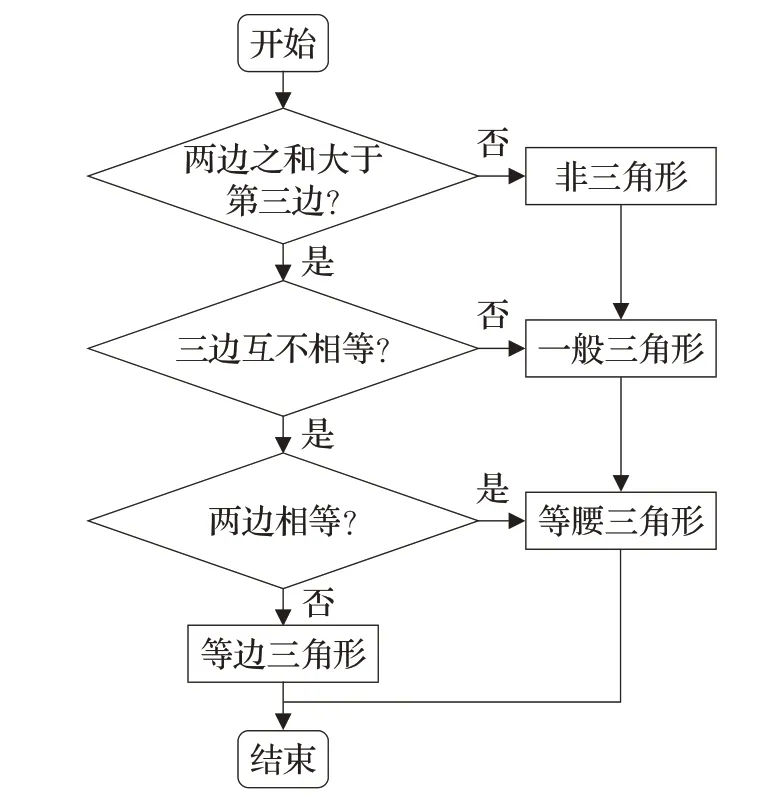
图8 三角形类型判定程序流程图Fig.8 Flowchart of triangle type judgment program
以下是插桩后的三角形类型判别MATLAB源代码:


4.2.2 构造适应度函数
算法是否需要进行迭代的依据是个体的适应度值,适应度函数的构造是测试操作模块的关键技术,也是SC-ChOA算法应用于测试数据自动生成的重要环节,测试数据的生成转化为使用SC-ChOA算法寻找目标函数的最优解的过程,因此适应度函数的构造将影响算法在测试数据自动生成中的效率。适应度函数使用分支谓词的分支距离计算,如表3所示。

表3 分支谓词的距离构造函数Table 3 Distance constructors for branch predicates
评价测试数据的好坏的一个重要标准是程序执行过程的覆盖率,计算覆盖率首先需要对被测程序的分支进行插桩,再对被测程序的目标路径进行插桩。覆盖率公式为:

其中,Xi表示第i分支的测试数据,x表示该分支的值,f(i)表示第分支的覆盖率。若f(i)≤0表示覆盖该分支,则令f(i)=0;若f(i)>0,则该值就是测试数据和分支的距离,值越大意味着测试数据离分支越远。总的适应度函数公式如下:

其中,F的取值范围在(0,1]之间,值越大则表示测试数据越好。当F=1时,表示该测试数据可完全覆盖该目标路径。
4.3 应用与分析
实验选取7个常用的程序作为基准程序,这些程序具有代表性,不仅包含选择结构、循环结构及复杂的嵌套结构,还含有算术运算符、关系运算符和逻辑运算符及整型、浮点型、字符型、字符串等数据类型,常被用于测试数据生成领域。程序的具体描述,其程序ID、变量数、分支数、搜索范围和程序描述如表4所示。
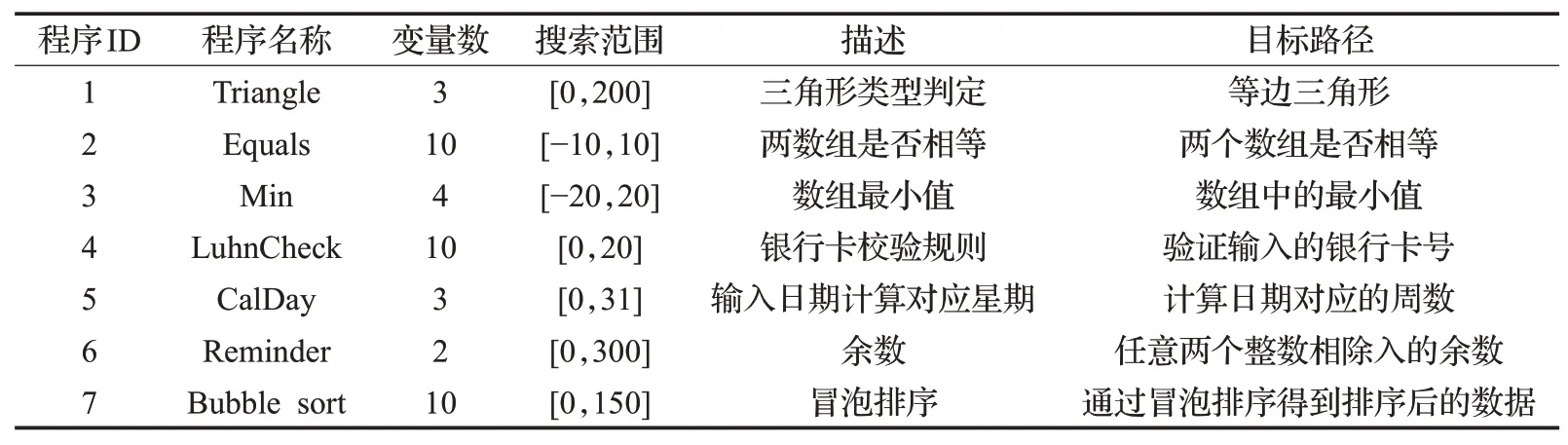
表4 测试基准程序Table 4 Test benchmark
为保证实验的公正性,3种算法在某些参数设置上保持一致,如群体大小、最大迭代次数等,其他参数参考其他文献设置,并使用迭代次数、覆盖率、生成测试数据数及运行时间为评价标准。
以三角形类型判定程序为例,通过三种算法进行实验比较,取平均值为评价标准。实验结果的相关数据如表5所示。

表5 三角形类型判别程序实验结果Table 5 Experimental results of triangle discriminator
由表5可知,改进算法SC-ChOA和标准ChOA比GA算法具有更高的效率,且覆盖率均达到了100%,而GA覆盖率只达到了90%,这是因为GA算法未生成覆盖目标路径等边三角形的测试数据。虽然标准ChOA和改进算法SC-ChOA的覆盖率都达到了100%,但是SC-ChOA在生成覆盖目标路径的测试数据时,生成测试数据总数仅有517个、所用的迭代次数只有14次,而ChOA相对于SC-ChOA产生了较多的冗余测试数据,且所用的迭代次数远大于SC-ChOA。因此,SC-ChOA相比于ChOA和GA在生成满足条件的测试数据效率方面及降低所用迭代次数上均具有一定的优势。为了更直观地看出三种算法在生成测试数据上的对比效果,图9是程序1使用三种算法生成覆盖目标路径的测试数据总数和迭代次数的直方图。
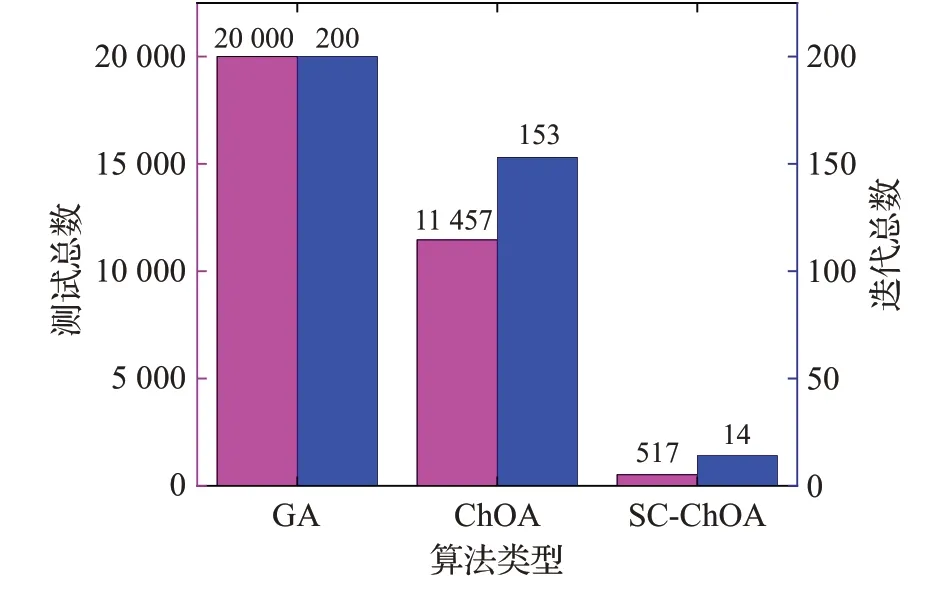
图9 程序1生成的测试数据总数和迭代次数Fig.9 Total number of test data and number of iterations generated by program 1
使用和三角形类别判定同样的方法及参数设置对表2中其他测试程序进行对比实验,为了更直观地看出SC-ChOA算法与其他两种算法在生成测试数据方面的效率,图10(a)和(b)是生成满足目标路径的测试数据所生成的测试数据总量及迭代总数。
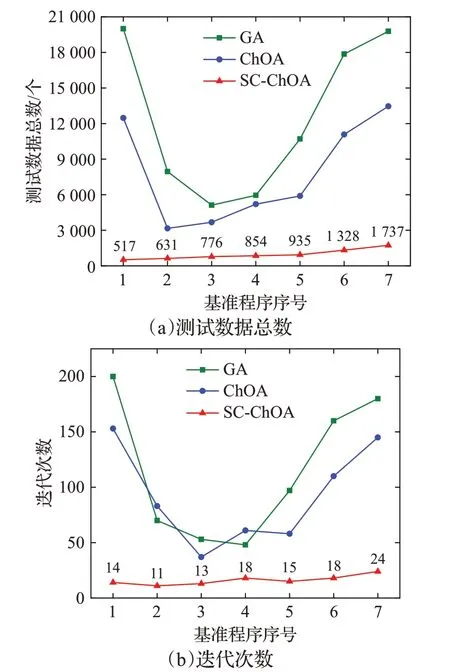
图10 七个基准程序测试数量和迭代次数对比Fig.10 Comparison of number of tests and number of iterations for seven benchmarks
由图10可以看出,本文提出的SC-ChOA算法生成满足目标路径的测试数据总数和此过程所用的迭代次数的折线图均在ChOA和GA下面,这说明了改进的SC-ChOA算法不仅提高了测试数据生成的效率,减少了冗余数据的生成,还降低了生成满足条件的测试数据所使用的迭代次数,这是因为在标准ChOA引入了正余弦扰动因子和非线性衰减收敛因子,使算法更好地平衡全局和局部搜索能力,避免算法陷入局部最优,减少了迭代次数,进而降低了冗余数据的生成。因此,SCChOA算法相比于其他两种算法在测试数据生成效率方面更具有优势。
图11是对七个基准程序进行10次实验所使用的运行时间,可明显看出,SC-ChOA算法很大程度上降低了在生成满足条件的测试数据的运行时间,这归因于SC-ChOA算法的寻优精度和收敛速度优于其他两种算法。
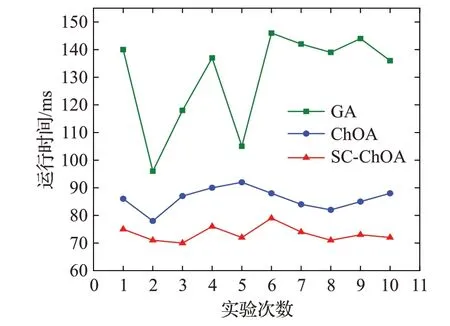
图11 七个基准程序三种算法运行时间Fig.11 7 benchmark program run-time of three algorithms
综上所述,本文提出的改进算法SC-ChOA可有效平衡整体和局部搜寻,不仅在测试数据生成的覆盖率上有所提高,还降低了生成测试数据的迭代次数和时间,进而改善了测试数据的生成速率和效果。
5 结束语
为提高测试数据的生成效率,本文对标准ChOA进行改进提出引入多攻略的正余弦扰动黑猩猩优化算法并将其用于测试数据生成方面。首先,引入拉丁超立方初始化种群,增加种群的多样化;其次,对标准ChOA算法进行改进,并提出非线性衰减收敛因子,用于权衡算法的全局勘察和局部开采能力,缩短算法的收敛时间,进而加快收敛速度;另外,在黑猩猩每次迭代过程中融入正余弦扰动因子,阻止算法陷入局部范围搜索,而导致算法出现停滞现象;最后,使用测试函数与标准ChOA算法及GA算法进行实验对比,验证算法的有效性,并将其应用于测试数据生成领域。通过基准程序对三种不同算法进行实验对比,结果表明,本文提出的算法SC-ChOA更加有效,可以应用于软件测试的全过程。在未来的工作中,将进一步思考如何将该算法与其他智能优化算法进行合理的融合,使其更好地应用于测试数据的生成及并行测试中。

