基于非奇异terminal滑模控制的车辆横向控制算法研究

扎西顿珠，格桑曲珍

(西藏农牧学院电气工程学院，西藏 林芝 860000)

无人车技术的兴起是要实现车辆的无人驾驶，主要利用各种传感器充当各种器官来感知车辆周围的环境参数，利用多种控制算法构成的控制器去模拟大脑作出各种决策，车辆执行机构根据车辆控制器给出的指令作出相应的动作，如转向、刹车、加速、停车等动作。其中，车辆路径跟踪是无人车的一个重要功能，而车辆的横向控制则是车辆路径跟踪系统中的技术关键。各国针对车辆横向控制算法做了深入研究，取得了丰硕的成果。Hui Zhang等[1]建立了车辆非线性模型，设计出最优控制器，使得车辆的侧滑角和偏航角限制在规定水平，从而实现了车辆的横向控制。Oudghiri M等[2]针对不确定Takagi-Sugeno(T-S)车辆模型的特点，设计出了相关容错控制(FTC)算法，利用该算法设计出了车辆横向控制器。Li B等[3]将横摆角速度误差和侧滑角误差作为输入，以横摆力矩和后部转向角作为输出，控制车辆沿着期望路径行驶。Pérez J等[4]认为车辆横向控制时，车辆方向盘速度和位置控制十分重要，并针对这两个因素设计出了基于模糊逻辑控制器的仿真人类驾驶行为的级联控制算法，该算法经测试后显示具有良好的控制性能。

车辆数学模型具有非线性、强耦合、时变等特点，所以横向控制对控制器的要求较高。滑模控制算法适用于非线性系统，具有结构简单、鲁棒性强、可靠性高等特点。本研究设计了滑模控制器来实现车辆的横向控制，完成了车辆的路径跟踪系统。传统的滑模控制器设计了一个线性滑动面，通过施加控制使系统达到滑动模态，从而跟踪误差逐渐收敛到零，虽然可以通过调整滑模面参数来调整误差收敛到零的速度，但是不可能在有限的时间内使系统误差收敛到零。为了解决该问题，通过构造一个引入了非线性函数的滑模面来实现系统误差在有限时间内收敛到零，即基于terminal滑模控制算法[5]。但是，基于terminal滑模面虽然解决了系统误差有限时间内收敛到零的问题，但是还存在滑模变结构控制固有的系统抖振问题，由此提出了相应的改进算法，将控制率中的符号函数sgn替换为修正的饱和函数sat，从而有效减小系统抖振。

1 车辆横向控制数学模型的建立

1.1 车辆二自由度数学模型

为了简化控制器的复杂度，车辆模型作出了一定的假设[6]：忽略车辆悬架，则车辆在z轴无位移、无俯仰、无侧倾；车辆在行驶期间，车轮相对滑动；车辆侧向加速度小于0.4 g，轮胎侧向力处于线性区间。当满足上述假设后，车辆模型可简化为二自由度数学模型，如图1所示：

图1 车辆二自由度模型Fig.1 Vehicle two degree of freedom model

(1)

由牛顿第二定律并结合式(1)可得车辆在横向和横摆两个自由度上的数学模型，如式(2)所示：

(2)

式(2)中，m为车辆的质量，Cf和Cr分别为车辆前后轮的侧偏刚度。

1.2 基于预瞄机制的横向数学模型

车辆行驶过程中，通常是以本车位置为基础，在车辆前方某一固定距离处的道路选择一预瞄点，通过预测车辆质心与所选择的预瞄点之间的相对位置，从而不断调整前轮转角，实现路径实时跟踪[7]。基于预瞄机制的横向数学模型如图2所示。

图2 预瞄机制的横向数学模型Fig.2 Lateral mathematical model of preview mechanism

分析图2中的几何关系，可以得到如下关系式：

(3)

式(3)中，yL为车辆中心线到预瞄点处的距离，即横向偏差；εL为车辆质心线与预瞄点处的切线之间的夹角，即航向偏差。DL是预瞄距离，KL为路径曲率。

(4)

矩阵A、B、C中，

2 基于预瞄机制模型的综合偏差设计

滑模变结构控制构造了滑模切换函数，只要使其趋于零，则系统误差也会趋于零。将系统误差作为滑模切换函数的参数，但存在横向偏差和航向偏差两个误差参数，为了简化系统控制模型，将这两个系统误差参数进行比例化融合为一个误差，将该融合误差作为滑模面构造参数。横向偏差与航向偏差两者的比例化融合为综合偏差e，公式如式(5)所示：

e=k1yL+k2εL

(5)

式(5)中，k1>0，k2>0，k1+k2=1。

3 非奇异terminal滑模控制器的设计

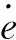
3.1 等效控制设计

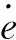
(6)

式(6)中，p与q都是正奇数，且p>q，β>0。

(7)

(8)

3.2 切换控制设计

设计切换控制usw为：

(9)

则非奇异terminal滑模变结构控制系统的总控制率u为：

u=ueq+usw

(10)

系统稳定性分析，定义Lyapunov函数为：

(11)

对上式求导并联立式(6)～(10)可得：

(12)

因此，本研究设计的非奇异terminal滑模控制必定会控制系统进入滑动模态，从而系统稳定。但是如此设计切换控制usw必定会带来较大的系统抖振，为了削弱系统抖振，将符号函数sgn用饱和函数sat替代：

(13)

4 仿真实验验证

为了验证所设计的非奇异terminal滑模控制器对车辆横向控制的有效性，利用MATLAB软件中的simulink模块进行编程，从而实现车辆横向控制的验证试验。车辆参数如表1所示，设置k1=0.6,k2=0.4,p=6,q=9,η=0.3,β=5,ζ=0.9。

表1 车辆参数Tab.1 Vehicle parameters

4.1 收敛速度分析

为了比较非奇异terminal滑模控制器相对于传统滑模控制器能够更加快速地进入滑模状态，从而使得跟踪误差趋于零[10]，仿真了非奇异terminal滑模控制器和传统滑模控制器对于同一段期望路径的跟踪过程，仿真结果如图3所示：

图3 非奇异terminal滑模和传统滑模跟踪过程Fig.3 Non-singular terminal sliding mode and traditional sliding mode tracking process

分析图3可得，非奇异terminal滑模控制器相较于传统滑模控制器，在跟踪期望路径时能够更加快速地使跟踪误差收敛于零。

4.2 抖振分析

为了削弱非奇异terminal滑模控制器给被控系统带来的抖振，将控制器中的sgn函数改进为饱和函数，图4中的(a)和(b)分别为采用sgn函数的非奇异terminal滑模控制器和采用饱和函数的非奇异terminal滑模控制器的前轮转角响应。

由图4和表2可得，采用饱和函数sat的非奇异terminal滑模控制器相较于采用符号函数sgn的非奇异terminal滑模控制器，可大幅度削弱车辆前轮转角抖振幅度，抖振幅度有效削弱90%～95%。

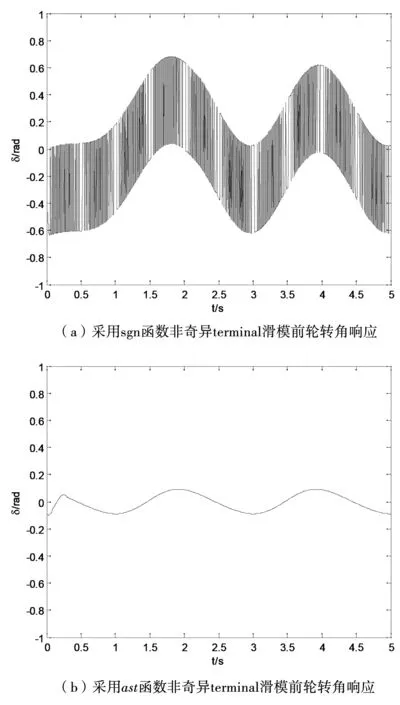
图4 前轮转角响应Fig.4 Front wheel angle response

表2 前轮转角抖振幅度和减小百分率对比表Tab.2 Comparison of buffeting amplitude and reduction percentage of front wheel angle

5 结论

针对车辆数学模型的非线性、强耦合、时变性等特点，设计了一种基于非奇异terminal滑模控制器，不仅适用于非线性系统，还能使系统误差在有限时间内收敛到零。同时，为了削弱系统抖振，设计了饱和函数sat来替换符号函数sgn，利用MATLAB中的simulink进行了车辆横向控制仿真实验。仿真结果表明，非奇异terminal滑模控制器相较于传统滑模控制器，在跟踪期望路径时能够更加快速地使跟踪误差收敛于零，采用饱和函数sat的非奇异terminal滑模控制器相较于采用符号函数sgn的非奇异terminal滑模控制器，可大幅度削弱车辆前轮转角抖振幅度，抖振幅度有效减小90%～95%。