单细胞RNA测序数据的聚类研究

汪 颖，张立莹

(大连交通大学，辽宁 大连 116028)

0 引言

信息化快速发展，数据急速增加，需要更有效的聚类算法解决单细胞RNA测序数据分析问题。生物学研究中，传统的批量RNA测序方法(RNA-seq)可以一次处理成千上万个细胞，并得到变异的平均水平。但是，没有两个细胞是完全相同的，而单细胞测序则可以揭示出每个细胞独特的微妙变化，甚至可以揭示全新的细胞类型。单细胞RNA测序大大提高了人们对生物系统的了解，而mRNA要翻译成蛋白质才能发挥作用。但在大多数转录组和蛋白组联合组学文献中，mRNA和蛋白质的相关度只有0.4～0.6，从RNA到真正发挥功能还有很长的一段路要走，这是用RNA测序预测功能的劣势[1]。单细胞RNA测序(单细胞测序)通过揭示具有高分辨率的单个细胞的异质性，彻底改变了转录组学研究。聚类已成为识别细胞类型、描述其功能状态和推断潜在细胞动力学的常规分析手段。目前，关于RNA测序技术的生物信息学分析还很薄弱，仅凭KEGG通路分析、GSEA基因分析很难得到实质有用的信息。针对RNA测序数据进行有效分类成为一种必然趋势，目前已存在一些聚类工具，如SC3[2]、SSCC[1]、Seurat[3]和CIDR[4]等，这些算法提高了数据聚类精度，但往往具有较高的计算复杂度。采用SCC策略，bigScale采用卷积策略通过贪婪搜索算法，将相似的单个单元合并为巨型单元。虽然这些聚类策略在某种程度上达到了一定的聚类效果，但仍有很大的改进空间。

聚类是分析单细胞RNA测序数据的重要分析手段，但快速扩展的数据量可能使该过程在计算上具有挑战性。已有的SSCC方法是目前比较有效的方法，在保证一定聚类精确性的基础上将计算复杂度从O(n2)降低到O(n)[1]。但SSCC在计算过程中使用的仍是传统的相似度度量方法，其对于高维稀疏数据集的计算存在一些弊端。为了克服这些弊端，构建了一个新的聚类公式，以识别可能属于相同真实集群的数据点。与当前的解决方案相比，此聚类方法考虑了附近数据对于聚类分类的影响，方案考虑得更全面，有更高的聚类准确度。考虑到聚类算法对于大规模单细胞测序数据分析的重要性，提出了一种新的聚类框架，针对单细胞测序，构建了二次相似性度量。已有工作表明，对于广泛的数据分布，随着维数的增加，传统的相似性(如欧几里德范数或余弦测度)变得不那么可靠(Beyeret al.，1999)[5]，因为一些数据集在高维空间中变得稀疏，传统的相似性度量可信度较低(Beyeret al.，1999)[5]，因此许多基于这些度量的聚类方法对于高维稀疏数据预测精度不高，效果不好。故而，利用二次相似性度量构建相似矩阵、利用传统度量构建相似矩阵，基于共享邻居排序，构建二次相似性度量矩阵。

二次相似性度量是基于共享最近邻(SNN)[6]的概念，考虑了周围邻居数据点的影响。确切地说，一对样本数据之间的相似性度量是由初步度量即传统相似性度量、二次度量基于共享邻居排序构建相似性度量构成。在高维情况下，SNN度量比相关的主要度量更稳健，并产生更稳定的性能(Houleet al.，2010)[7]。SNN技术已成功应用于一些聚类问题(Ertoězet al.，2003；Guhaet al.，2000；Jarvis和Patrick，1973)[8]。受这些早期应用的启发，根据共享邻居的排序，重新定义了新的相似性度量。

1 方法

使用欧几里得距离(也可以使用其他合适的度量)来计算传统相似度矩阵，基于共享邻居排序，给出二次相似度度量公式w(xi,xj)[6]。通过公式w(xi,xj)构建新的二次相似性度量Y(xi,xj)及公式Y(xi,xj)进行计算，通过轮廓值来评价结果的准确性。

1.1 构建二次度量w(xi,xj)

对于第i个样本数据xi(i=1,2,3,…,n)，使用传统相似性矩阵，列出k个最近邻居，即：

KNN(xi)={xi1,xi2,xi3,…,xik}

式中，xik表示的是xi的第k个最近邻居。

如图所示，图1中，1，2，3，…，9表示xi和xj的邻居x1，x2，x3，…，x9，取k=6，则：

KNN(xi)={x2,x6,x3,x7,x9,x4}

KNN(xj)={x1,x5,x3,x7,x8,x4},

其分别表示样本xi和xj的6个最近邻居。xi，xj的共享邻居为SNN(xi,xj)={x3,x7,x4}。仅当xi和xj具有至少1个共享的KNN时，才保留边w(xi,xj)。

图1 图中数字1～9表示样本x1～x9Fig.1 Figure 1～9 represent sample x1～x9

对于任意的xi，xj{i,j=1,2,3,…,n}，样本xi，xj的二次度量定义如下：

k表示最近邻居集合的大小，rank(v,xi)代表样本v在xi的最近邻居集合KNN(xi)中的排序。

因此，共享最近邻居(SNN)图捕获了两个样本在邻域中的连通性方面的相似性[6]。与其他传统相似性不同，在度量中，两个样本之间的相似性还考虑了该样本与邻居样本(公共最近邻)之间的相似性来确认。与传统相似性相比，SNN更适用于高维数据样本的相似性度量。

1.2 改进的二次相似性度量Y(xi,xj)

二次相似性度量w(xi,xj)在某种程度上避免了传统相似性度量对于高位稀疏数据的弊端，在此基础上进行改善，除了考虑到了最近邻居对于样本相似性度量的影响，还考虑了绝对相似度度量(传统度量)对样本间相似性度量的影响。利用改进的二次相似性度量可以纠正边缘数据样本错误分类问题，改进的二次相似性度量公式如下：

d(xi,xj)表示xi，xj的传统相似性度量，d(xi,xj)与Y(xi,xj)成反比，说明在同样的w(xi,xj)条件下，两样本之间传统距离越大相似度相对降低，反之，传统距离越小相似度相对增强。

1.3 聚类方法

在可用的处理大规模单细胞RNA数据方法中，一般采取的是聚类，采样之后进行分类，其过程为数据初步处理，数据初始分类，利用聚类方法进行重新分类，聚类检验。利用k-means[9]和k-medoids[10]对传统距离构造相似性度量矩阵，利用二次相似性度量w(xi,xj)矩阵和改进的二次相似性度量Y(xi,xj)矩阵进行预测和计算。为了获得独立于聚类算法的评估结果，使用轮廓值来检查这些特征工程方法的全局性能，进行评估。

1.4 轮廓值

轮廓值[11]用于测量真实标签与原始标签之间的一致性，以更好地预测数据。轮廓是基于其紧密性和分离性的比较，轮廓值显示了具体数据在子集中的位置。针对给定具有n个样本和聚类方案的数据集，计算每个样本的轮廓值。对于每个样本xi，定义一个特定的值Si，即轮廓值。

图2Fig.2

取数据集中的任何样本xi，图2表示第i个样本xi属于集合A。当集合A中包含除xi以外的其他对象时，可以计算出A(i)，即xi与A中的所有其他对象的平均距离。考虑到与A不同的聚类C，即xi与C的所有对象的平均距离，记为D(i，C)。计算完平均距离之后，选择这些数字中最小的一个，表示如下：

这就像对象xi的第二个最佳选择，如果它不能容纳在集群A中，集群B将是最接近的集合。图2中，当A本身被丢弃时，平均而言，集合B与样本xi最近，因此了解数据集中每个对象的邻居是非常有用的。

式中，ai是样本xi与其自身聚类中的样本的平均差异，而bi是样本xi与任何其他聚类的最低平均差异。需要注意的是，必须假设簇k的数量大于1。Si的值范围从-1～1。接近1的值意味着样本xi与其聚类完全匹配，而接近-1的值意味着样本xi如果被分类到其相邻聚类中则更合适。

对于广泛的数据分布，传统的相似性(例如欧几里得范数或余弦度量)随着维数的增加而变得不那么可靠。使用一个二次相似性基于共享最近邻居(SNN)的概念，一对数据点之间的相似性是它们之间交点的函数，由主要指标(例如欧几里得范数)确定固定大小的邻域。在高维中，SNN度量比主要度量更有效，并具有更稳定的性能[6]。SNN技术已成功应用于某些聚类问题，由此基于两个数据点共享邻域的排名来定义新的相似性。

2 结果

2.1 结果比较

在图3～8中，每个点代表一个单元。使用原始数据直接计算的轮廓值显示在X轴，使用通过Y(xi,xj)计算的轮廓值显示在Y轴。在1处的轮廓值表示标签和特征之间的完美匹配，在-1处的轮廓值表示该单元可能被错误分类。每个图中的百分比表示对角线上方的细胞分数，即Y(xi,xj)二次相似性度量比传统相似性度量的方法更好。测试的3个数据是Kolodziejczyk数据集、Pollen数据集、Usoskin数据集。

图3 Pollen数据集，当k=11时使用k-medoids方法进行计算Fig.3 Pollen data, k-mediods is used to calculate when k=11

图4 Pollen数据集，当k=11时使用k-means方法进行计算Fig.4 Pollen data, k-means is used to calculate when k=11

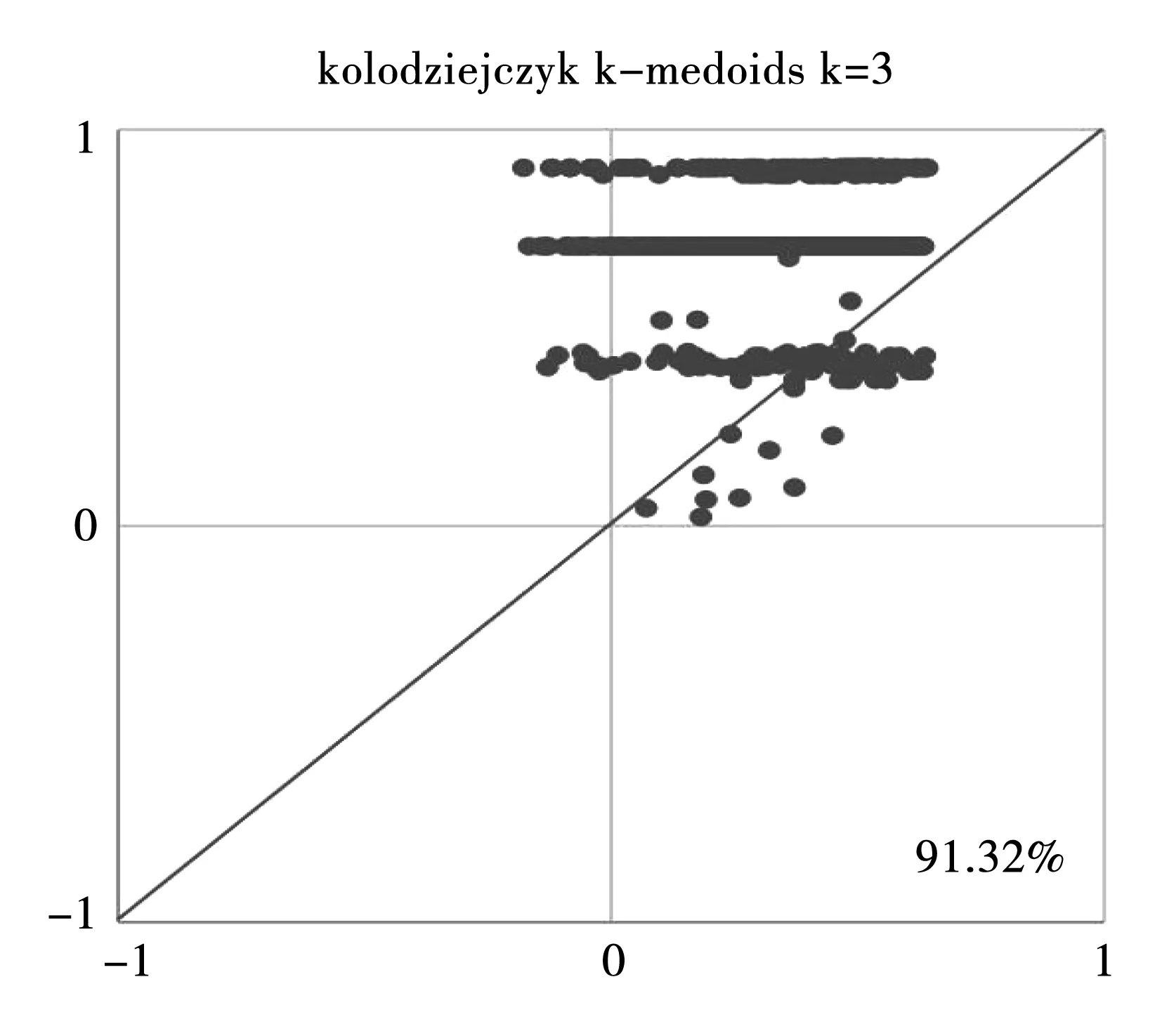
图5 Kolodziejczyk数据集，当k=3时使用k-medoids方法进行计算Fig.5 Kolodziejczyk data, utilization of k-medoids when k=3

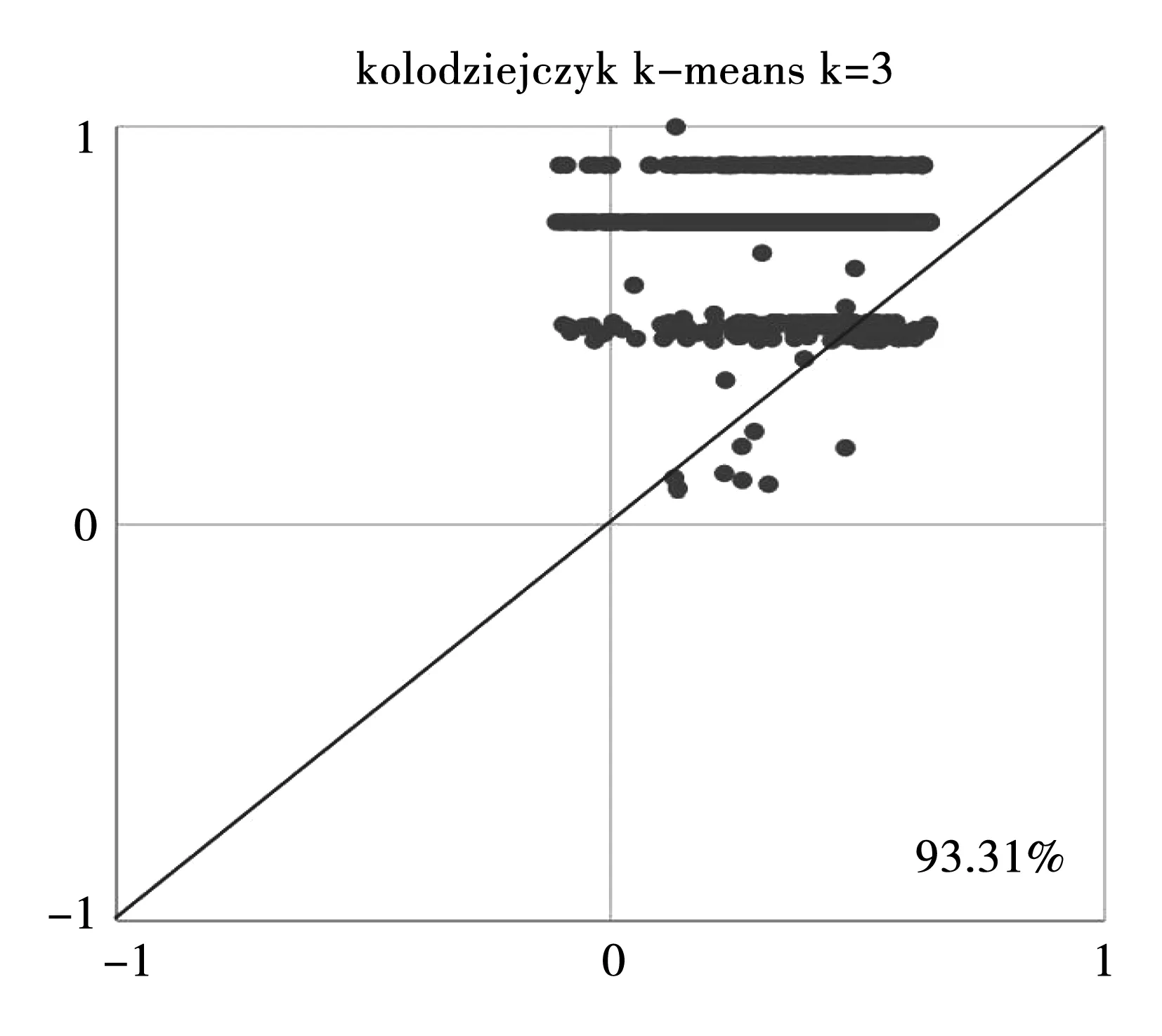
图6 Kolodziejczyk数据集，当k=3时使用k-means方法进行计算Fig.6 Kolodziejczyk data, utilization of k-means when k=3

图7 Usoskin数据集，当k=4时使用k-medoids方法进行计算Fig.7 Usoskin data, utilization of k-medoids when k=4

图8 Usoskin数据集，当k=4时使用k-means方法进行计算Fig.8 Usoskin data, utilization of k-means when k=4

从6个图形中能发现，除了利用k-medoids方法针对Usoskin数据集的计算结果(图7)不太理想之外，其他的轮廓值图形结果均显示利用本研究提出的二次度量Y(xi,xj)比传统相似性度量总体来说轮廓值体更高一些，效果更好。3个数据库的计算结果显示，Y(xi,xj)二次相似性度量的计算结果要比传统距离相似性度量的结果更为准确，准确率是研究进行的先决条件。

2.2 使用的单细胞测序数据集

使用4个单细胞测序数据集来评估特征空间中的聚类性能，包括Kolodziejczyk数据集[12]、Pollen数据集[13]、Usoskin数据集[14]。下面列出了这些数据集的详细描述。

Kolodziejczyk数据集[12]包含704个具有3个簇的细胞，这些簇是在不同培养条件下从小鼠胚胎干细胞获得的。通过使用Fluidigm C1系统并应用SMARTer试剂盒获得cDNA和大约10 000个基因以高测序深度(平均每个细胞9 000 000个读数，>80%读数映射到Mus musculus基因组GRCm38，外显子>60%)进行分析。 用于Illumina文库制备的Nextera XT试剂盒。

Pollen数据集[13]包含249个细胞，其中11个簇是从皮肤细胞、多能干细胞、血细胞、神经细胞等中获得的。基于C1单细胞自动准备集成流体回路的低或高测序深度，SMARTer超低RNA试剂盒和Nextera XT DNA样品制备试剂盒用于描述单个细胞的基因表达谱(每个细胞约50000个读数)。

Usoskin数据集[14]包含622个具有4个簇的小鼠神经元细胞，即具有肽能的伤害性感受器官，含有非肽能的伤害性感受器，含有神经丝的细胞和含有酪氨酸羟化酶的细胞。用机器人细胞采集装置挑选神经元细胞，并在RNA-seq(114 000个读数和每个细胞3574个基因)之前将其定位于96孔板的孔中。

3 讨论

单细胞转录组分析中，通常需要根据单个细胞的基因表达水平对其进行分组，以便每组对应具有特定功能的细胞类型。这种分析有助于描述组织中的细胞组成及区分发育阶段，从而更好地理解组织的生理学和病理学及发育过程。由于存在生物和技术差异，一种理想的全基因组单细胞数据聚类方法能够有效区分细胞类型和高基因表达水平。针对一些高维较稀疏数据集，提出了二次相似性度量Y(xi,xj)，该相似性度量在一定程度上克服了传统相似性度量对高维稀疏数据可信度较低的弊端。二次相似性度量Y(xi,xj)将为广泛存在的高维稀疏数据集提供一种较为有效的相似性度量，为进一步研究和分析提供有利条件。