基于多任务差分进化的飞行器近似优化方法

陈 晅，朱华光，龙 腾，叶年辉，史人赫

（1. 北京理工大学，北京，100081；2. 北京宇航系统工程研究所，北京，100076）

0 引 言

作为一类复杂的系统工程，飞行器设计过程中通常需要针对不同工况及任务需求进行系统方案优化，且不同优化任务之间往往存在一定的相关性与相似性（例如，不同工况下的最优气动外形设计）。为了实现相似优化任务的高效协同求解，多任务优化的概念应运而生[1]，核心思想是利用相似任务间的优化知识迁移对多个优化任务同时求解。近年来，国内外学者针对多任务优化理论与方法开展了广泛研究[2～4]。

随着数值计算技术和计算机仿真技术的发展，计算流体力学、有限元分析等高精度建模方法在飞行器设计优化中得到广泛应用。为了降低高耗时仿真模型分析成本，代理模型方法在工程设计领域得到了广泛应用[5]。近年来，基于代理模型的进化算法（Surrogate Assisted Evolution Algorithm，SAEA）[6～8]成为了工程优化领域的研究热点。在国内外研究方面，Long等[9]提出了一种基于知识迁移抽样的代理模型辅助差分进化算法，通过序列迁移优化高效求解新优化任务。然而，如何实现飞行器不同优化设计任务的协同高效求解，仍是当前飞行器设计优化理论研究与工程实践中需要解决的重要问题。

为提高多个相似飞行器优化设计任务的综合优化性能并降低优化总成本，提出一种基于多任务差分进化的近似优化方法（Multitasking Differential Evolution Based Approximation Optimization Method，MTDE-AOM），并通过标准数值测试和翼型多任务优化工程案例对MTDE-AOM的优化性能进行验证。

1 径向基函数方法介绍

径向基函数（Radial Basis Function，RBF）是一种插值型代理模型，该代理模型方法可表示为径向函数线性加权形式[10]：

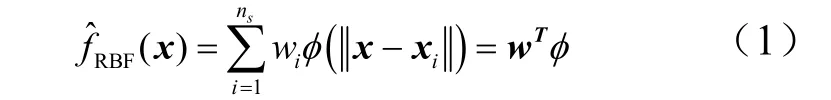
式中φ（·）为核函数。采用逆多二次函数作为RBF核函数；w为权重系数矢量，可以由下式求解得到[11]

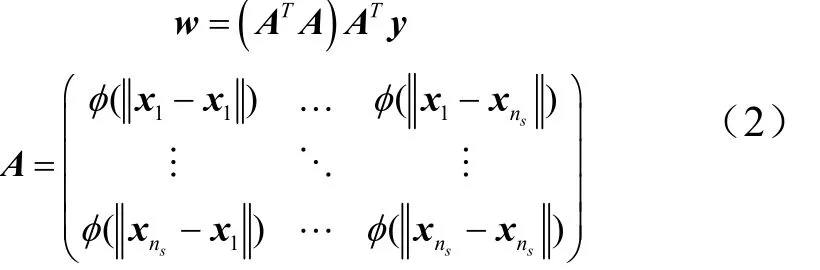
式中ns为构造代理模型的样本规模。

2 MTDE-AOM介绍

2.1 飞行器多任务优化问题建模

飞行器多任务优化问题数学模型如式（3）所示：

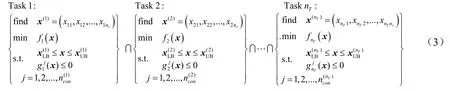
式中x(i)为第i个任务的设计变量；nv为设计变量维度；fi为第i个优化任务的目标函数；与分别为第i个任务的设计变量下界和上界；为第i个任务的第j个约束函数；为第i个任务的约束函数的数量nT为优化任务数量。对于约束优化问题，采用罚函数法构建增广目标函数，将其转换为无约束问题进行求解。

2.2 MTDE-AOM流程

MTDE-AOM算法流程如图1所示，具体步骤如下。

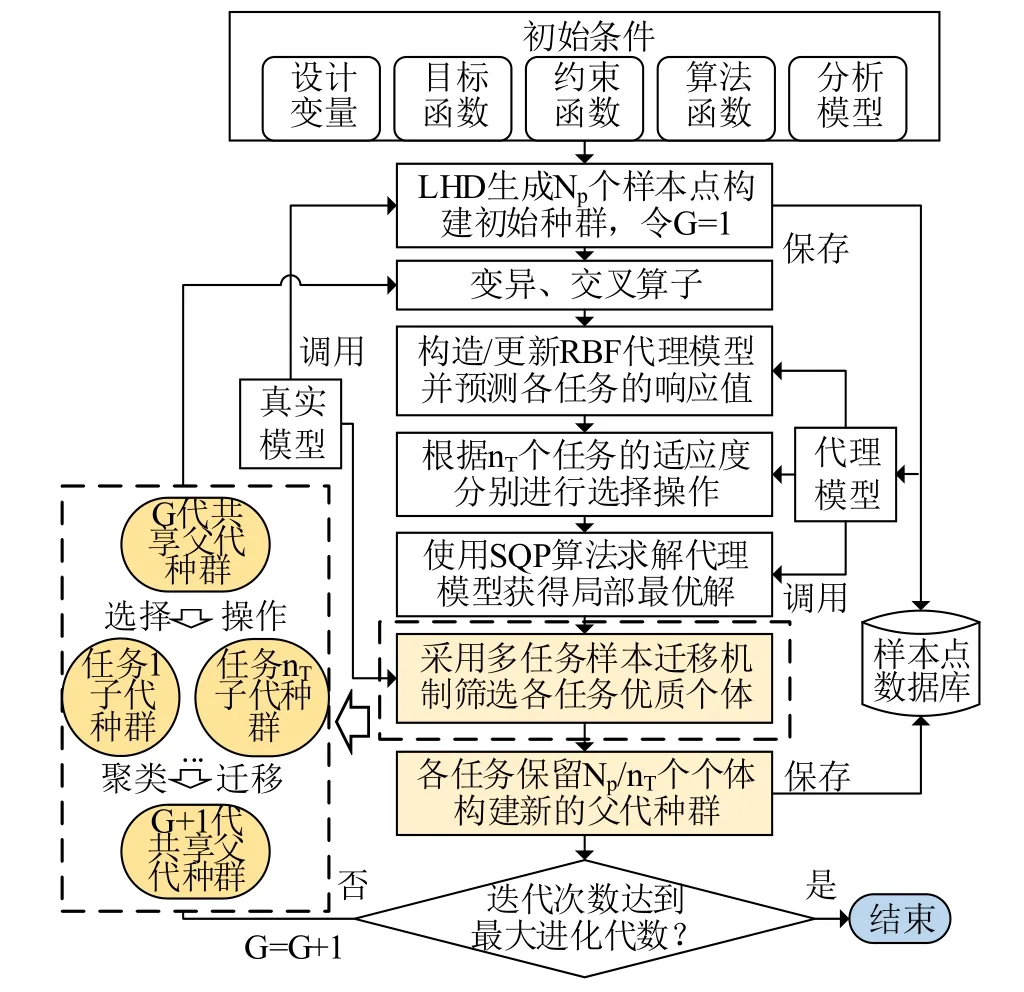
图1 MTDE-AOM方法流程 Fig.1 Flowchart of MTDE-AOM

a）初始参数设置，包括初始种群规模Np、最大迭代次数Gm、初始缩放因子F0、交叉概率CR；定义多任务优化问题，包括任务数量nT、问题维度nv，各优化任务目标函数、约束函数以及设计空间等。令当前进化代数G=1。

b）采用拉丁超方试验设计方法在归一化设计空间中获取Np个初始样本点xdata，计算初始样本点xdata关于各任务的增广目标函数值Fi(xdata)并添加到样本数据库中。

c）进化代数G=1时，将作为所有优化任务共享父代种群；当进化代数G≥2时，将更新后的子代种群作为新父代种群。其中，父代个体xj可表示为对共享父代种群进行变异和交叉操作[11,12]。

1）对于父代个体jx，通过变异操作生成变异个体vj，vj可以表示为从而获得变异种群采用Rand/1变异策略实现变异操作。此外，使用自适应缩放因子更新方法[13]在优化过程中动态调节缩放因子大小，具体如式（4）所示：

式中F0是初始缩放因子；Gm是最大迭代次数；G是当前进化代数。

2）对种群个体xj和vj进行交叉操作生成试验个体并获得试验种群

d）使用样本数据库中所有样本构造各任务增广目标函数的RBF代理模型并预测试验种群个体各任务的响应值

e）使种群个体针对每个任务分别进行选择 操作[12,13]，经选择后获得nT个子代种群每个子代种群个体数为Np，第i个优化任务的子代种群可以表示为

f）对式（3）中的目标函数与约束函数构造RBF代理模型，并采用序列二次规划算法求解，将获得的各优化任务局部最优解添加到子代种群中。

g）采用多任务样本迁移机制，即通过聚类分析获取各优化任务优质子代个体，共同组成下次迭代共享父代种群，具体如下：

1）使用k-means算法对当前子代种群xgen进行聚类，对于第i个优化任务的种群，聚类个数为Np/nT个。将该类别个体中的最优个体表示为

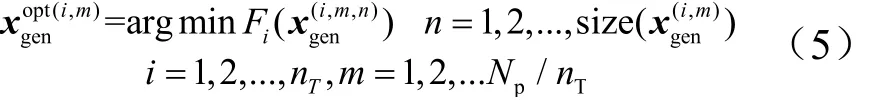
式中表示第i个优化任务对应的子代种群经过聚类操作以后的第m个类别的所有个体；表示该类别的个体数量；表示第i个优化任务第m个类别的最优个体。本步骤中，通过聚类分析筛选出各优化任务优质子代个体。

2）保留第i个优化任务每个类别的最优个体，并将其加入该优化任务的新子代种群中，将Tn个优化任务的子代种群合并，组成个体总数为pN的新子代种群，并更新样本库。

h）判断是否达到最大种群进化代数，若没有达到，令G=G+1,返回步骤c；否则，优化过程结束，输出各优化任务的最优解。

3 标准数值测试算例

为了验证MTDE-AOM算法的多任务优化性能，选取了文献[9]中6个标准数值测试算例，与标准多任务差分进化算法（Multitasking Differential Evolution，MTDE）[4]及标准差分进化算法（Differential Evolution，DE）[11]进行对比，对MTDE-AOM的收敛性和优化效率进行验证。

3.1 算例描述与参数设置

MTDE-AOM算法的参数设置如表1所示，MTDE算法各参数与MTDE-AOM保持一致，DE算法的种群规模为 2Np，其余参数与表1一致。各算法分别对各算例连续优化20次，统计优化结果中可行解的最优解、均值、最差解、标准差进行对比。

表1 MTDE-AOM算法参数设置 Tab.1 Parameter Configuration of MTDE-AOM

对于约束优化算例，MTDE-AOM、MTDE和DE算法参数设置与表1一致，最大模型调用次数设为

3.2 优化结果及分析

各优化算法的优化结果对比如表2所示，各算法的平均模型调用次数如表3所示。优化结果表明，对于SC问题，3种优化算法均能够收敛至各优化任务的最优解附近。随着优化问题维度增加，MTDE与DE算法的全局收敛性变差。以EP20优化问题为例，对于优化任务1，MTDE-AOM优化结果最优性与MTDE、DE算法相比分别提升50.21%和97.37%；对于优化任务2，MTDE-AOM的优化结果最优性分别提升12.31%和95.91%。由MTDE与DE算法对比结果可知，采用多任务样本迁移机制能够加快进化种群优化收敛。在优化效率方面，相比于MTDE方法，MTDE-AOM由于引入了RBF代理模型做近似优化，有效降低了真实模型调用次数，其平均计算成本降低了25.40%～41.23%。对于G09约束问题，相比于MTDE，在模型调动次数基本相同的情况下，最优性分别提升7.95%和10.36%，相比于DE，最优性提升7.30%和14.63%。

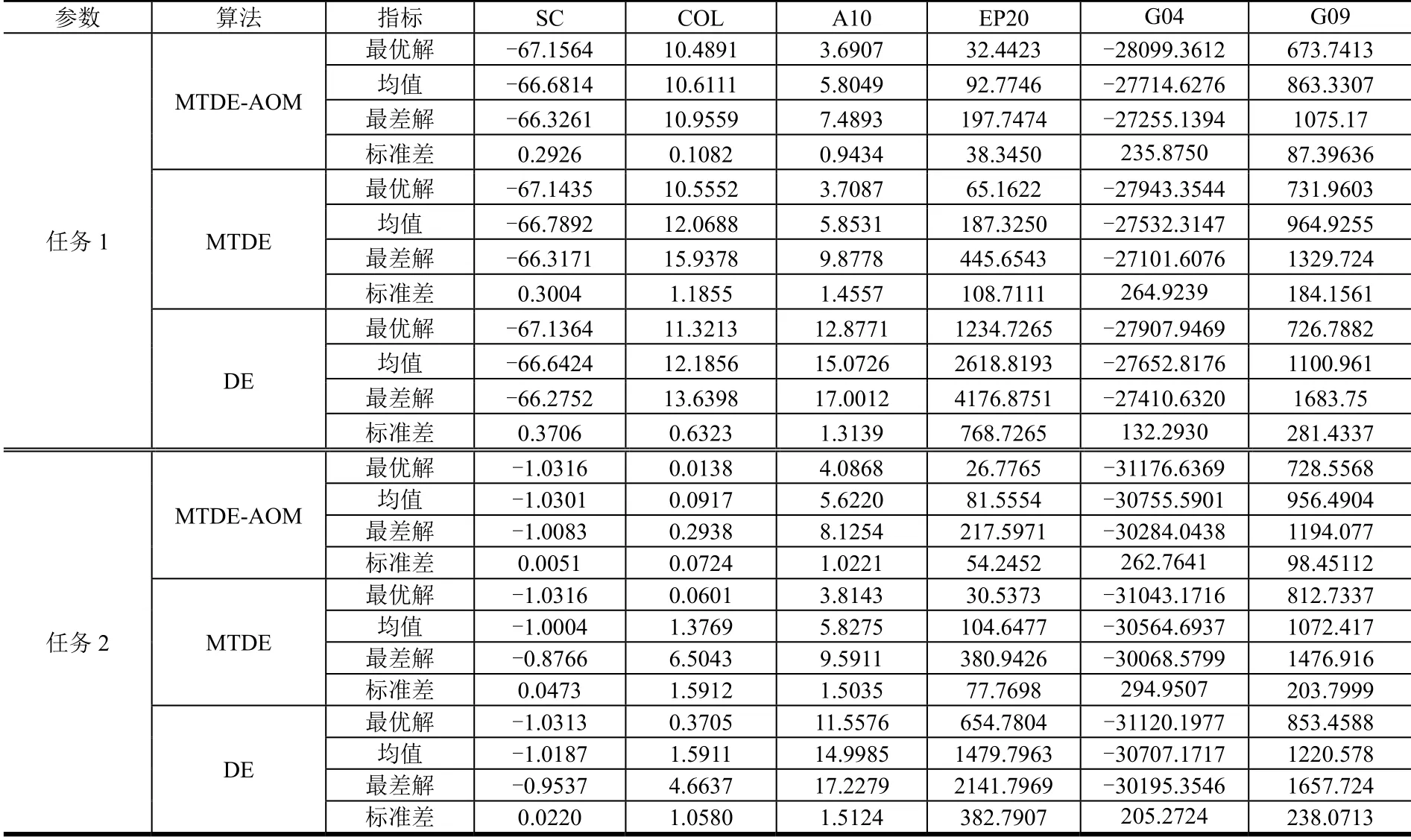
表2 MTDE-AOM、MTDE和DE标准算例优化结果对比 Tab.2 Comparison of MTDE-AOM, MTDE, and DE on Numerical Benchmarks

表3 平均模型调用次数对比 Tab.3 Comparison of Average Number of Function Evaluations of Benchmarks

4 翼型多任务优化工程案例

4.1 翼型多任务优化问题

为进一步验证提出的MTDE-AOM的工程实用性，将该方法应用于翼型气动多任务优化问题[9,14]。对多种工况下的不同基准翼型进行优化，改善翼型的升阻力特性，优化模型如式（7）所示：

式中C lCd为翼型升阻比；tmax为翼型的最大相对厚度；t0与Cd0分别为基准翼型的最大相对厚度与阻力系数。各优化任务的设计工况与基准翼型如表4所示。

表4 设计工况与基准翼型表 Tab.4 Design Conditions and Benchmark Airfoils

4.2 优化结果对比分析

采用MTDE-AOM和DE算法求解式（7）所示翼型气动多任务优化问题，最大模型调用次数 NFEmax均设置为1500。

表5给出了在两个工况下使用MTDE-AOM和DE两种算法优化前后翼型的参数对比。图2给出了优化前后翼型外形的对比，各优化任务优化后的翼型升阻比分别提升了102.26%和10.27%，对于任务1，与初始翼型相比，优化翼型最大厚度略有降低，上翼面中部变平，减小阻力，下翼面后部内凹程度变大，因此有效地提升了翼型升力。对于任务2，翼型整体向上隆起，下翼面向内凹陷，因此优化后翼型弯度变大，从而有效提升了亚声速翼型升力。

表5 翼型优化结果 Tab.5 Result of Airfoil Optimization

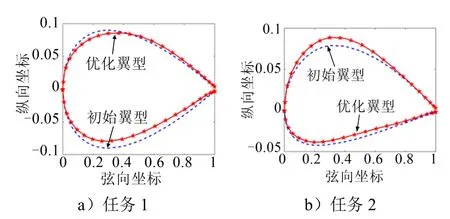
图2 翼型优化前后对比 Fig.2 Comparison of Initial and Optimized Airfoils

5 结束语

为提升相似的飞行器系统优化任务求解性能，定制一种多任务样本迁移机制，从而利用进化过程中各优化任务的优质个体信息，实现多个相似设计优化任务协同优化。优化结果表明，MTDE-AOM算法与MTDE、DE算法相比，在全局收敛性、计算效率以及鲁棒性等方面具有优势。未来将提出的算法应用到飞行器装备系统技术指标多任务优化工程实践。