一溴化锶分子低激发态的光谱特性研究*

伍冬兰 郭自依 周俊杰 阮文 曾学锋 谢安东

(井冈山大学数理学院,吉安 343009)

采用内收缩多参考组态相互作用(ic-MRCI)方法和相对论有效芯赝势基(aug-cc-pV5Z-PP),优化计算一溴化锶(88Sr79Br)分子14 个低激发电子态的电子结构和单点能.为了获得更加精确的光谱参数,引入Davidson、核价电子相关和相对论效应修正单点能,根据优化修正得到的单点能分析获得了最低5 个束缚态的势能曲线和偶极矩.利用LEVEL8.0 程序拟合修正的势能曲线,得到各束缚态的光谱常数、分子常数和振动能级等光谱性质参数.对比发现本文计算的结果与实验值吻合较好,最后给出了跃迁性质参数Franck-Condon 因子和辐射寿命.这些光谱特性参数为进一步实验测量和构建分子激光冷却方案提供理论支持.

1 引言

碱土金属化合物由于其特殊的电子组态得到许多实验与理论光谱学家的青睐[1,2],其中碱土金属卤化物在天体物理学、催化和高温化学中应用特别广[3,4],尤其是锶原子由于其强的吸附谱线,在天体物理学领域引起广泛的兴趣[5−7].最近,Caffau等[7]证明锶原子是银河系化学演化的重要示踪剂,此外,它被认为是大量恒星中重要的中子俘获元素,由于锶原子存在于所有的恒星中,因此,一卤化锶分子的能级、跃迁偶极矩和相应的光谱常数对天文学家和天体物理学家来说具有相当大的参考价值,对其光谱和卤化物光谱的研究也已成为一个热门话题.由于该类化合物基态(X2Σ+)和第一、二激发态(A2Π,B2Σ+)的势能曲线和核间距非常相似,导致光谱密集不便于区分.随着激光器的出现,国内外学者采用不同的理论计算方法和各种实验光谱技术,对碱土金属一卤化物溴化锶(88Sr79Br)的光谱特性已做了大量研究.1985年,Torring等[8]首先通过实验分析了溴化锶(88Sr79Br)的微波转动光谱,拟合获得了分子常数;Ernst等[9]通过微波光学偏振光谱学测量了X2Σ+和B2Σ+态的超精细结构,得到了分子的平衡核间距参数.Keijzer等[10]通过连续波激光诱导荧光光谱测量了部分光谱常数.Coxon等[11]采用高分辨率激光激发光谱分析了A2Π–X2Σ+跃迁态的光谱特性,并且研究了离解能和拟合获得了分子常数.后来,Gurvich等[12]通过火焰分光光度法测量了离解能为(78.4±4.4)kcal/mol,同时Hildenbrand[13]通过气体平衡质谱法获得了分离能为(78.7±2.2)kcal/mol.Ernst和Schröder[14]对B2Σ+–X2Σ+跃迁带进行微扰分析,后来在振动光谱实验中观测到了微扰现象.Dickinson和Coxon[15]分析了A2Π–X2Σ+跃迁带系的微扰情况,另外Schröder和Ernst[16]测量了B2Σ+–X2Σ+的振转能级.Castano等[17]研究了其分子化学发光动力学,Gunduz和Akman[18]测定高分辨率分子溴化物.此外,由于Sr 原子和Br 原子都是重元素,88Sr79Br分子可能具有显著的自旋-轨道耦合(SOC)分裂和相对论效应,这些现象都会影响光谱常数和跃迁性质的计算精度,导致有些理论计算值与实验值存在一定的相差,而这些光谱特性参数能为进一步实验测量分子光谱性质提供理论支持.

本文利用Davison 修正的内收缩多参考组态相互作用方法(ic-MRCI+Q),考虑核价电子关联和相对论效应修正优化计算88Sr79Br 分子的最低两个解离极限对应的14 个激发态在全空间的电子结构和单点能量.通过分析单点能,获得势能曲线、电偶极矩和跃迁偶极矩,发现只有5 个势阱较大的束缚态,利用LEVEL8.0 程序拟合获得束缚态的光谱常数、分子常数和振动能级等,最后还给出了Franck-Condon 因子和辐射寿命等跃迁性质.

2 计算方法

由于Sr和Br 都属于重元素原子,采用MOLPRO2012.1 程序包[19],选取相对论有效芯赝势基(aug-cc-pV5 Z-PP)作为计算基组[20].

88Sr79Br 分子属于线型结构,为C∞υ点群.计算中使用阿贝尔子群C2υ代替C∞υ点群.两者的不可约表示有如下对应关系:Σ+=A1,П=B1+B2,Δ=A1+A2,Σ–=A2.计算中把88Sr79Br 分子的8 个轨道(4 个a1,2 个b1和2 个b2)确定为活性空间,分别对应Sr 原子的4s4p 轨道和Br 原子的4s4p 轨道,两者的最外层电子放入活性空间,内层26 个电子放入关联轨道,总共选用35 个电子作为关联能计算,余下的38 个电子被冻结在芯轨道.设置核间距R=0.18—0.66 nm,步长为0.01 nm,平衡位置附近步长为0.005 nm,优化计算88Sr79Br分子的单点能.优化计算中考虑Davidson 修正(+Q),核价电子关联和相对论标量效应修正,先用Hartree-Fock(HF)方法计算单组态波函数,然后用态平均全活性空间自洽场方法(SA-CASSCF)优化单组态波函数为多组态波函数[21,22],最后用内收缩多参考态相互作用方法(ic-MRCI)计算分子各个态的单点能量[23,24].分析单点能获得88Sr79Br分子最低的14 个激发态的势能曲线.

采用LEVEL8.0 程序[25]包求解径向Schrödinger 方程,拟合势能曲线能量点,获得各束缚态的光谱常数(绝热激发能Te、平衡核间距Re、谐性振动常数ωe和转动常数Be等),和分子常数(振动能级Gν、惯性转动常数Bν和离心畸变常数Dν).同时根据跃迁偶极矩,给出了Franck-Condon 因子和辐射寿命等跃迁性质.这些光谱和分子常数以及跃迁性质,为进一步实验测量88Sr79Br 分子激发态的光谱特性提供理论参考.

3 结果与讨论

3.1 束缚态的势能曲线和光谱常数

分析88Sr79Br 分子最低两个解离极限Sr(1Sg)+Br(2Pu),Sr(3Pu)+Br(2Pu)和离子对Sr+(2Sg)+Br–(1Sg),发现分别对应14 个激发电子态.采用内收缩的多参考组态相互作用方法(ic-MRCI+Q)和相对论有效芯赝势基aug-cc-pV5Z-PP,优化扫描计算获得88Sr79Br 分子精确的电子结构和单点能.为了便于直观分析,只把最低5 个束缚态的单点能绘于图1.根据能量和图分析得出这5 个束缚态分别为X2Σ+,A2Π,B2Σ+,C2Π和32Σ+,其中B2Σ+态出现了双势阱,A2Π和C2Π,B2Σ+和32Σ+都出现了避免交叉现象,分别对应R=0.356 nm和R=0.367 nm 位置,而A2Π和B2Σ+分别在R=0.350 nm和R=0.376 nm 两处出现了相交,这两个交点在考虑了自旋-轨道耦合之后会出现避免交叉现象,导致能量分布出现变化,后期研究论文中我们会详细讨论.利用LEVEL8.0 程序拟合修正的能量点得到各束缚态的光谱常数,结果列于表1,还列出了主要的电子组态分布及权重.为了便于比较分析,表中给出了其它的理论计算和实验值.本文获得的各束缚态的势能曲线的变化特征类似于同主族相同类型的分子体系MgBr[26]和CaBr[27]的变化特征,这也可以说明本文拟合的相关参数应该是可靠的.

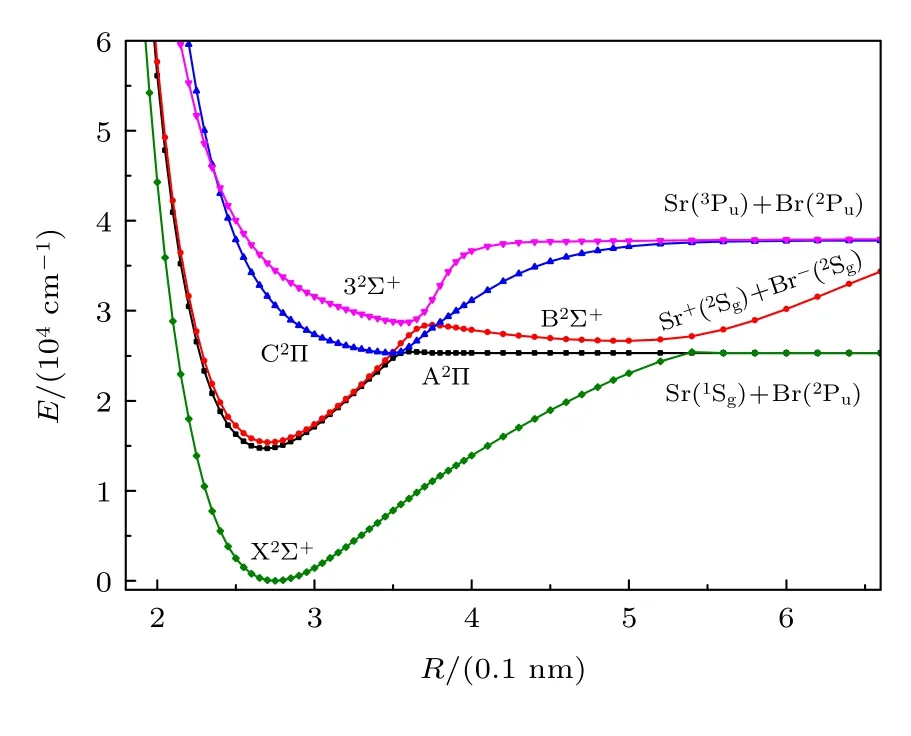
图1 88Sr79Br 分子5 个激发态的势能曲线Fig.1.The potential energy curves of 5 lowest electronic states of88Sr79Br.

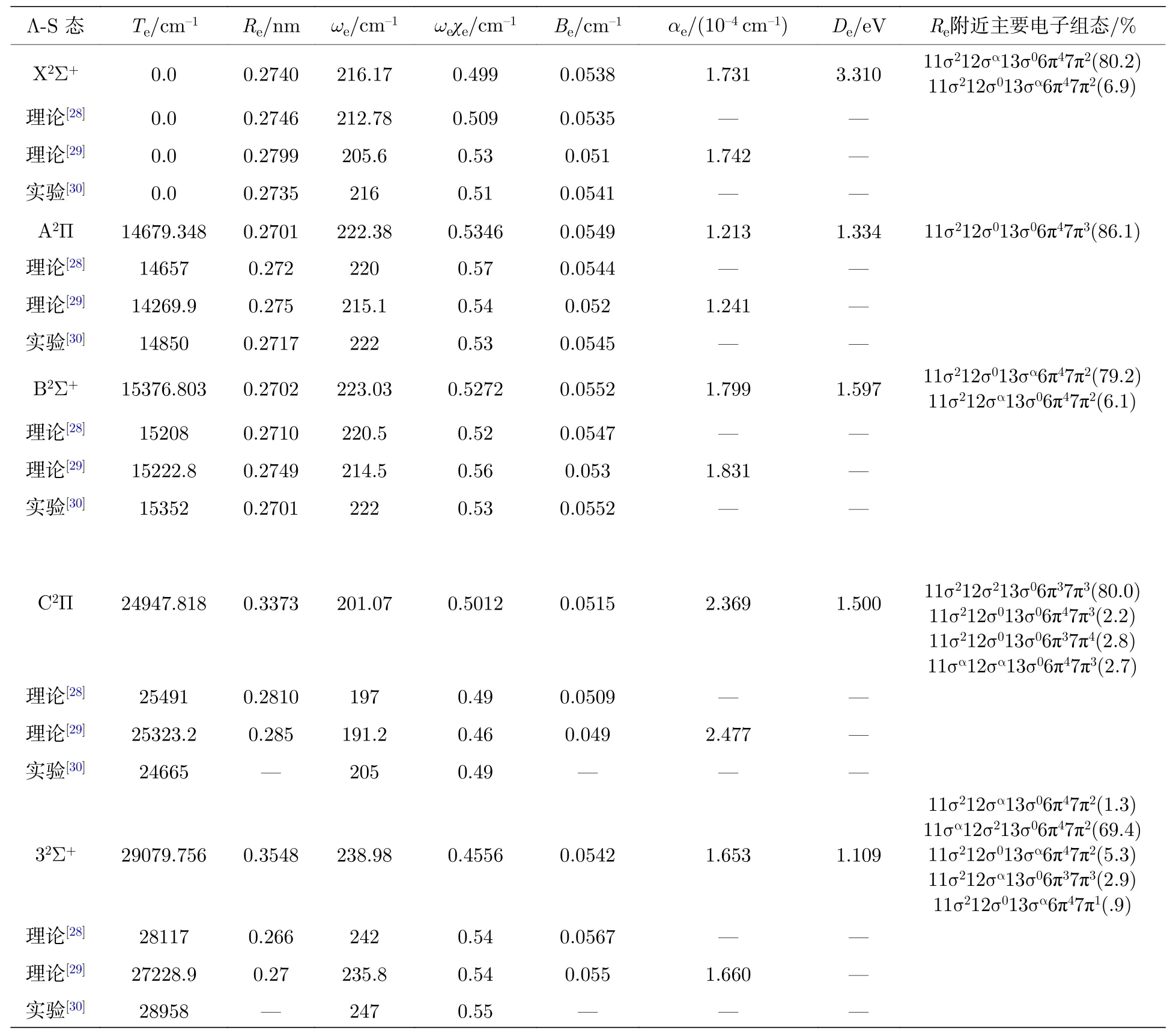
表1 5 个束缚态的光谱常数Table 1.The spectroscopic constants of the 5 lowest electronic states.

从图1 中可看出,基态X2Σ+为一个深势阱态势能曲线,从表1 中也发现离解能较大,结果3.310 eV 与实验值(78.4±4.4)kcal/mol=3.400 eV 吻合较好,两者都说明基态是一个比较稳定的电子态.在平衡位置附近主要的电子组态为11σ212σα13σ06π47π2和11σ212σ013σα6π47π2,表 明了使用多组态方法的必要性[31−33].通过对比分析文献[28]的计算数据发现,本文计算的光谱常数Re,ωe和Be更接近实验值[30],偏差分别为0.0005 nm,0.17 cm–1和0.0003 cm–1,这可能是由于文献[28]中采用了多组态相互作用方法,但是没有进行相关修正能量点,这样会导致光谱数据与实验值偏差较大,其他的光谱常数与文献[29]理论计算值也都比较接近,这可能是由于本文与文献[29]中采用的计算方法一样,也采取了相关修正,不同的是本文选用的计算基组更大.因此在计算光谱数据时需要采用高精度的计算方法和较大的基组,还需要考虑相关修正才能得出更加精确的光谱参数.通过与同主族相同类型分子体系计算得到的光谱常数相比,发现离解能小于理论计算结果BeBr(77.31 kcal/mol=3.343 eV)[31],MgBr(3.351 eV)[26]和CaBr(339.5 kJ/mol=3.518 eV)[27],平衡键长则大于计算值BeBr(0.1953 nm)[31],MgBr(0.2371 nm)[26]和CaBr(0.2604 nm)[27],这些对比说明88Sr79Br 分子相比BeBr,MgBr和CaBr 分子体系,稳定性更差,更容易离解,这些特性也符合分子结构稳定性质.

能量高于基态的电子态为激发态,根据能量的高低依次往上排开,其中能量稍高于基态的为第一激发态(A2Π),这个态与基态对应于同一个解离极限Sr(1Sg)+Br(2Pu),但离解能为1.334 eV,小于基态的3.310 eV,这说明两态相比,基态分子更加稳定.计算发现,A2Π 平衡位置附近主要的电子组态为11σ212σ013σ06π47π3,表明有一个电子从X2Σ+激发跃迁到A2Π,即12σ(13σ)→7π.A2Π的绝热激发能为14679.348 cm–1,与实验值14850 cm–1[30]有些相差,百分误差为1.15%,这可能是与C2Π 产生了避免交叉现象导致势能曲线发生变化的原因.光谱常数Re,ωe和ωeχe相比近来的理论计算结果,本文与实验值更接近,偏差分别为0.0017 nm,0.38 cm–1和0.0046 cm–1,Be与实验结果[30]也相差不大,但与近来的理论计算[29]更接近,偏差为0.0005 cm–1.

能量高于第一激发态的为第二激发态(B2Σ+),B2Σ+的势能曲线与基态和第一激发态分布不太一样,该态出现了双势阱,对应解离极限为离子对Sr+(2Sg)+Br–(1Sg).B2Σ+的绝热激发能为15376.803 cm–1,与实验值15352 cm–1[30]较接近,偏差仅为24.803 cm–1,这可能是由于B2Σ+与32Σ+出现了避免交叉现象的原因.拟合的光谱常数ωe,Re,ωeχe和Be与实验结果[30]吻合较好,偏差仅分别为1.03 cm–1,0.0001 nm,0.0028和0 cm–1.高于B2Σ+的为第三激发态(C2Π),离解能为1.500 eV,在R=0.356 nm 处与A2Π 产生了避免交叉现象,与A2Π 能隙为242.01 cm–1,不同的是C2Π 对应另一个解离极限Sr(3Pu)+Br(2Pu).本文同样给出了C2Π和32Σ+激发态的光谱常数,发现结果与实验值和近来获得的理论值相比其他的电子态误差更大些,这可能是由于电子态之间相互作用的影响.综上分析发现,本文获得的光谱常数与实验值和近来的理论计算值吻合都较好,有些参数比其他的理论计算值更接近实验值.这些高精度的光谱常数为进一步分析高激发态的光谱常数和跃迁特性提供较好的参考作用.

3.2 束缚态的振动能级和分子常数

利用LEVEL8.0 程序包[25]拟合优化计算得到的束缚态的单点能,分析了J=0 时各束缚态的全部振动态.为了便于比较分析,本文同时计算了88Sr79Br和88Sr81Br 分子的振动能级,表2 中只列出了88Sr79Br 分子各束缚态的前10 个振动态的振动能级Gν,惯性转动常数Bν和离心畸变常数Dν.计算结果表明,88Sr79Br 分子X2Σ+的0-0 跃迁带的分子常数Gν为0,Bν和Dν分别为0.054093和1.355×10–8cm–1,88Sr81Br的分子常数分别为0,0.053517和1.324× 10–8cm–1,与文献[11]中实验值相比,88Sr79Br的分子常数更接近实验值,Bν和Dν的相对误差分别为0.1%和4.1%,88Sr79Br 分子A2Π的0-0 跃迁带的分子常数分别为14970.08,0.054979和1.395× 10–8cm–1,88Sr81Br的分子常数分别为14786.59,0.054583和1.363× 10–8cm–1,与文献[11]中实验值相比,88Sr79Br的分子常数也更接近实验值,相对误差分别为4.8%,1.5%和3.4%.88Sr79Br分子B2Σ+的0-0 跃迁带的分子常数为15376.52,0.055152和1.384× 10–8cm–1,88Sr81Br的分子常数分别为15198.68,0.054972和1.371× 10–8cm–1,比较分析发现88Sr79Br 分子的分子常数与文献[16]中的实验值15355.79,0.055206和1.410× 10–8cm–1吻合更好,相对误差仅为0.1%,0.1%和1.9%.综合分析88Sr79Br和88Sr81Br的分子常数,说明88Sr79Br的分子常数更接近实验值,因此本文只给出了88Sr79Br的分子常数,而且数据应该是可靠的,表中还给出了更多激发态和更高振动态的分子常数.

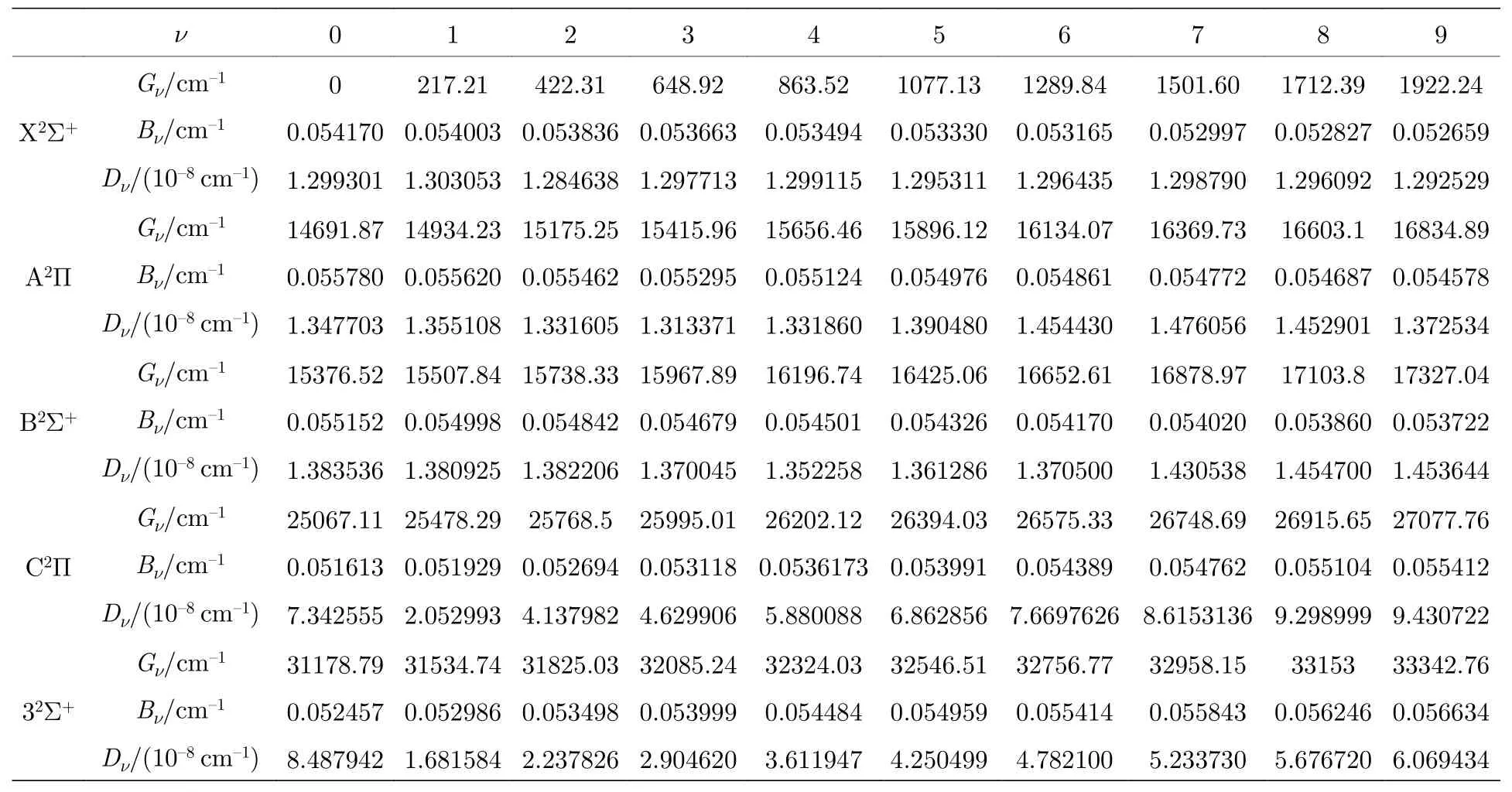
表2 88Sr79Br 分子5 个束缚态的Gν,Bν和Dν值Table 2.The values of Gν,Bν and Dν of 5 lowest electronic states for88Sr79Br molecule.

3.3 束缚态的电偶极矩

根据分子结构理论,分子的电偶极矩可以反映分子的成键性质.图2为各束缚态的电偶极矩随着分子核间距R的变化关系.

图2 88Sr79Br 分子5 个束缚态的电偶极矩Fig.2.The permanent dipole moments of 5 lowest electronic states of88Sr79Br.

分析图2 变化关系发现,当核间距增大到0.60 nm时,B2Σ+的电偶极矩达到最大值6.104 a.u.,这说明该分子离子特性较强,与前面分析该态对应离子对解离极限的结果是一致的;另外4 个电子束缚态的电偶极矩当核间距大于0.65 nm 后趋于零,表明这些束缚态最后都解离为中性原子.当核间距在0.354 nm 附近,A2Π和C2Π的偶极矩出现了极性反转,B2Σ+和32Σ+在0.366 nm 附近的偶极矩也出现了极性反转现象,分析发现这可能是由于出现了避免交叉现象引起的,这些特性与势能函数的变化趋势是一致的,与同主族相同类型的分子MgBr[26]体系也是一样的.

3.4 束缚态的跃迁特性

为了分析分子的跃迁特性,优化计算了各束缚态的跃迁偶极矩,图3为跃迁偶极矩的绝对值随键长的变化关系.从图3 中可看出,在Franck-Condon区域内,C2Π–X2Σ+的跃迁偶极矩的绝对值明显大于A2Π–X2Σ+的跃迁值.当核间距逐渐变大后,各束缚态的跃迁偶极矩最后都逐渐趋于0.通过拟合跃迁偶极矩获得各束缚态的Franck-Condon 因子,结果表明B2Σ+–X2Σ+的0-0 跃迁带的Franck-Condon因子对角化比较明显,具有最大值为0.825605,这些结果符合挑选激光冷却分子体系的条件,可以作为激光冷却的候选分子体系.其他跃迁带因子都没有明显的对角化,而C2Π–X2Σ+和32Σ+–X2Σ+的因子都非常小,几乎趋于0(表格没列出),这可能是由于两者的平衡核间距较大的原因.

图3 88Sr79Br 分子5 个束缚态的跃迁偶极矩Fig.3.The transition dipole moments of 5 bound states of88Sr79Br.

根据优化计算得到的跃迁偶极矩、Franck-Condon 因子、各束缚电子态的单点能和振动能级,获得了最低两个束缚激发态-基态跃迁的辐射寿命,计算公式如下[34,35]:

其中τv′为各激发态振动能级v′的辐射寿命;Av′和ΔEν′,ν′分别为爱因斯坦系数和能量差(单位为cm–1);TDM为平均跃迁偶极矩;qν′,ν′′为Franck-Condon因子,利用上式计算了各激发态到基态的跃迁辐射寿命.结果发现C2Π–X2Σ+和32Σ+–X2Σ+跃迁态由于Franck-Condon 因子非常小,导致寿命非常大,表3 中没有列出,因为这在实验上观测不到,表4中只列出了A2Π–X2Σ+和B2Σ+–X2Σ+两个跃迁态的辐射寿命.通过比较发现,B2Σ+–X2Σ+跃迁的v′=0 寿命为40.93 ns,与实验结果(42.2±1.6)ns吻合较好[36],相对误差为1.8%.A2Π–X2Σ+跃迁的v′=0 寿命为32.23 ns,与实验值(34.3±2.3)ns也比较接近[36].

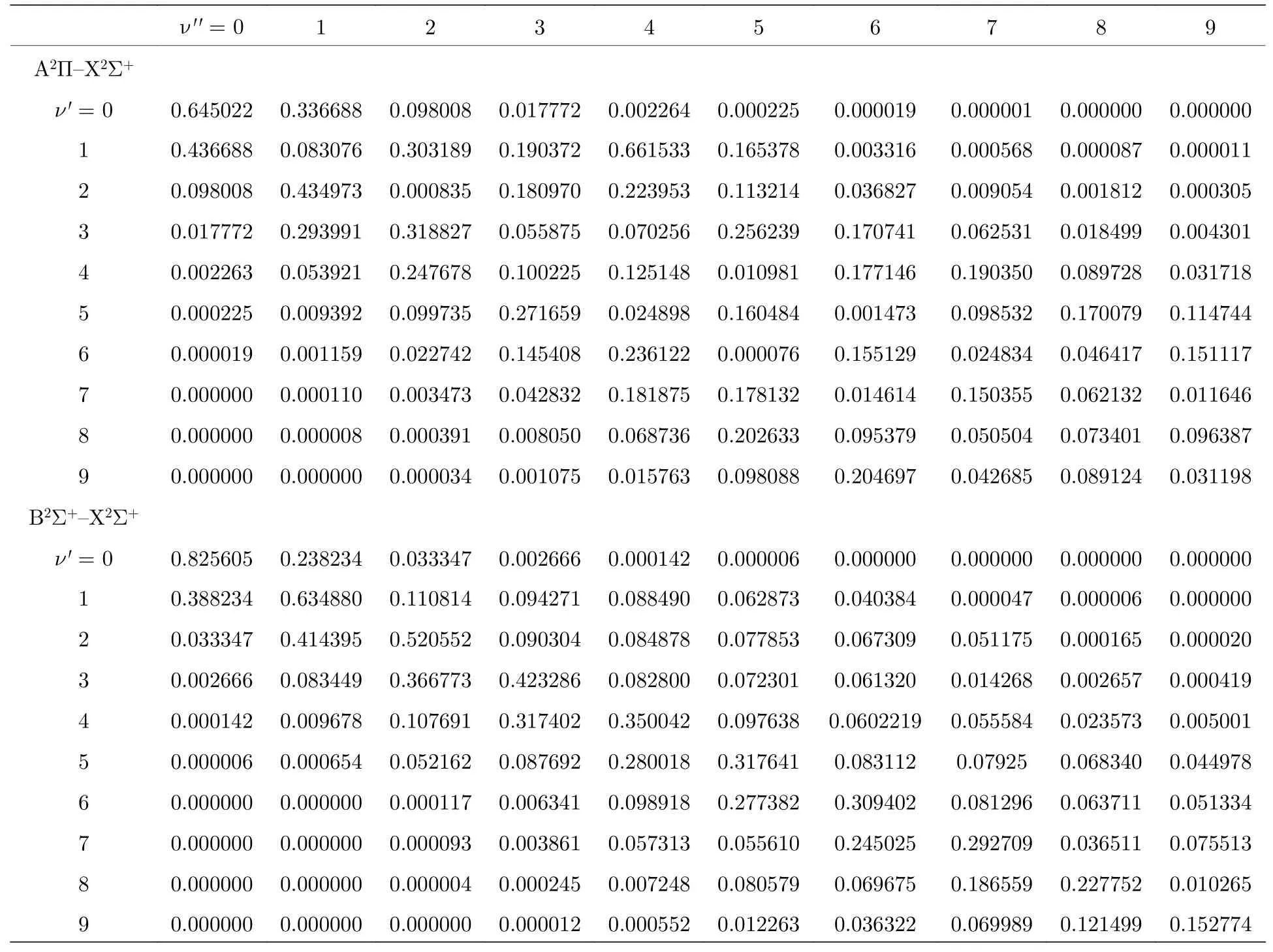
表3 88Sr79Br 分子A2Π–X2Σ+和B2Σ+–X2Σ+跃迁的Franck-Condon 因子Table 3.The Franck-Condon factors of the transitions A2Π–X2Σ+和B2Σ+–X2Σ+ of88Sr79Br.

表4 88Sr79Br 分子A2Π–X2Σ+和B2Σ+–X2Σ+跃迁的辐射寿命Table 4.The radiative lifetimes of the transitions A2Π–X2Σ+ and B2Σ+–X2Σ+ of88Sr79Br.

4 结论

本文利用内收缩多参考组态相互作用方法(ic-MRCI),结合考虑多种相关修正优化计算了88Sr79Br 分子最低14 个电子态的电子结构、单点能和偶极矩等.结果表明最低5 个束缚态都存在较深的势阱,其中以基态的势阱最深,说明该态最稳定,在实验中更容易观测到.根据各束缚态的势能曲线分布特性和电偶极矩出现了偶极矩反转现象,都说明是由于出现了避免交叉现象引起的.获得的光谱常数、振动能级和分子常数等与实验值的百分误差都在5%以内,同时给出了跃迁性质参量Franck-Condon 因子和辐射寿命,结果与实验值也吻合较好.本文获得了比较完善的低激发态的光谱跃迁特性,这为进一步实验测量和构建激光冷却方案提供理论支持.