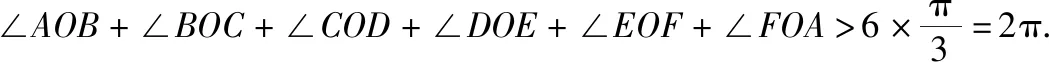四类求极值应用题的解题思路与方法

甘肃省高台县第一中学 王维斌

求极值类数学应用问题，与工农业生产、人们日常生活有着密切的联系，它要求学生运用“数形结合”的理论、思想、方法建立实际问题的数学模型，来解决实际问题.这对培养学生分析和解决问题的能力有很大的帮助.求极值类数学应用题由于涉及到的知识点多，综合性较强，考查的范围广，分值较高，已成为近年来高考的必考考点.因此学会和掌握这类应用题的解题方法与技巧，就能够为考生在高考中夺取高分奠定坚实的基础.

1 根据数列性质解决利息类问题

利息类问题虽然也属于增长率问题，但它具有自身的特点，同时由于高中生平时对银行这类储蓄问题比较陌生，很容易出错.所以，解决这类问题首先要搞清利率的两种计算方法.①单利计算：假设A元本金的年利息为Ar元，n年的利息为nAr元，那么n年后的本利之和为A+nAr=A(1+nr)元；②复利计算：第1年后的本利之和为A(1+r)元，第2年后的本利之和为A(1+r)2元(前一年的本利之和为后一年的本金)，这样n年后的本利之和为A(1+r)n.然后把它化归为等比(差)数列问题处理.

例1一对农村中年夫妻为了给他们的独生女儿积攒将来上大学的学费，从孩子一出生就在她每年生日那天到银行存上一笔钱.设某大学每年的学费为2 500元，上完四年本科共需1万元.考虑到通货膨胀因素，学费将以每年5%的速度递增.假设女儿出生那年银行存款年利率为7.5%，假定存款利息18年内不变.按复利计算，试问，当女儿到18岁上大学时，他们已经存足了四年的学费，那么每年生日那天应存入多少钱？

解：1万元学费，按5%的上涨率，18年后为10 000×(1+5%)18≈10 000×2.406 6=24 066(元).

解得x≈627.5(元).

答：他们每年生日那天应存入627.5元.

思路与方法：本题的计算要从孩子0岁时存款算起，1～18岁每年的利息与本金之和组成的数列为x(1+0.75)，x(1+0.75)17，……，x(1+0.75)18，根据等比数列的规律，按照复利息计算公式计算.

2 运用数形结合思想解决产品设计类问题

工厂和车间经常要加工或生产某种规格的机械零件，要在用料最少(最省)的前提下，使零部件的面积或长、宽符合某种要求.这实际上就是在限制条件下求最值类问题，可以运用“数形结合”思想通过建立数学模型来解决.

图1

解：如图1，设正十字形的长DG为y，宽AB为x，其外接圆直径DH=d，正十字形的面积为S，外接圆周长为C.

由正十字形的对称性，可知

S=xy+x(y-x)=2xy-x2

①

d2=x2+y2

②

C=πd③

3 通过解不等式组解决整点问题

对于点P(x，y)，当其横坐标和纵坐标都为整数时，我们称点P为整点.在实际问题中，这里的x，y通常都为自然数，即x，y∈N.像诸如药剂最佳配料类整点问题，就可以通过解不等式组来解决.

例3配制A，B两种药剂，需要甲、乙两种原料.已知配A种药需要甲料3 mg，乙料5 mg；配B种药需要甲料5 mg，乙料4 mg.现有甲料20 mg，乙料25 mg.若A，B两种药至少各配一剂，问最多一共能配几剂？

解：设A，B两种药分别能配x剂和y剂，x，y∈N*，则有不等式组

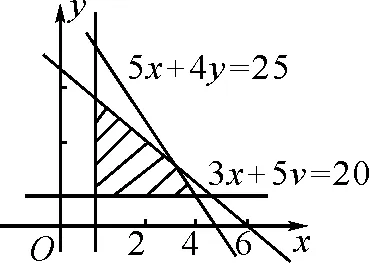
图2

所以，在至少各配一剂的条件下，A，B两种药最多一共能配5剂.

思路与方法:本题是把最多配剂(求极大值)问题转化为解不等式组的问题，由于所围成的区域受不等号方向的影响，所以解题时要防止区域出错；另外还要注意寻求符号要求的整点，比较后再决定取舍.

4 用逆反建模法解决动态类求证问题

在现实生活中，我们有时会遇到一些随着时间、地点、空间等不断变化的动态类问题[1]，从正面思考时往往感到难以入手，这时我们不妨从逆反思维的角度尝试去解决.

例4有若干个距离彼此不等的机场，每一机场都有一架飞机起飞，飞到离它最近的机场降落.试证明：任一机场降落的飞机不能超过5架.

图3

证明：如图3，假设有一机场O降落的飞机超过5架，不妨设为6架，它们分别来自A，B，C，D，E，F这6个机场.

∵A到O的距离与A到B的距离不等，

∴OA

同理，OB

∴在△OAB中，AB为最大边.

这与6个角之和为2π矛盾，故假设不成立.

因此，任一机场降落的飞机不能超过5架.

思路与方法：本题的证明如果从正面入手显然有困难，所以我们不妨从反面思考，假设有某一机场降落的飞机超过5架，看能否通过几何模型来导出矛盾.本题的证明过程并不复杂，关键是要通过观察、分析、类比、联想、转化等方法[2]，将实际问题巧妙地转化为数学模型.

求极值类应用题涉及代数、三角、立体几何、解析几何等众多知识领域，且题型多样，有一定的难度.当然，针对不同的类型，解题的思路与方法也不同，例如本文中介绍的“运用数列性质、数形结合、解不等式组、逆反建模”等，其中最重要的是要学会运用“数形结合”的解题思想；要了解和熟练掌握常见类型题的解法，特别是数学建模的方法.在此基础上，仔细观察，认真思考，合理联想，勤加练习，长此以往，就能够逐步接近“举一反三”高效解题的目标.