基于径向基函数的无网格法分析非均匀左手介质填充波导

翁倩茹 卢楚杰 潘思辰 谢恩德

1(成都工业学院智能制造学院 四川 成都 611730)2(广东工业大学计算机学院 广东 广州 510006)

0 引 言

左手介质是一种介电常数ε和磁导率μ均为负数的新型人工介质，在这种介质中电场(E)、磁场(H)和坡印亭矢量(S)三者的方向呈现左手螺旋方向[1]。Pendry等[2]结合周期性排列的开口谐振环(Split ring resonators,SRRs)和金属杆，首次物理实现了具有负折射的左手介质，自此之后，左手介质的理论和应用研究呈现爆发式的增长。其中一个重要的研究方向，就是用左手介质代替传统介质应用于各种微波毫米波器件。近年的研究发现，在波导中填充非均匀左手介质会表现出奇异的传播特性。例如在填充左手介质的矩形波导和圆波导中，都发现了低于截止频率传播的后向波传播特性[3-7]。而这些奇异的电磁特性在小型化波导、后向波天线等毫米波集成电路器件中具有非常高的应用价值。

近年来，具有连续变化折射率的非均匀左手介质(又称为梯度折射率左手介质)受到研究人员的广泛关注。这种新型人工介质可以改变电磁波的传播方向和传播相位，在变换光学、调整电磁波束和电磁波隐身结构设计方面具有广泛应用[8-10]。对于波导中左手介质非均匀性的精确求解，是各种毫米波和光波集成电路元器件设计和最优化的基础。

除了一些特殊情况(例如均匀左手介质加载或内衬波导[3-4,6])，大多数非均匀左手介质填充波导结构不能求解析解。因此需要利用数值方法对于波导的特征值进行近似计算，常用的数值计算方法包括有限元法、时域有限差分法、矩量法和变分法等[11-13]。

然而，对于有限元法和时域有限差分法等方法，需要对研究区域进行网格的划分，其未知数分布在整个研究区域中。并且非均匀介质区域需要高质量的网格划分，其求解精度与网格划分的质量密切相关，因而这些基于网格划分的数值方法占用大量的计算、存储和时间资源。

近几年，基于径向基函数(Radial basis functions,RBFs)的无网格方法受到了学界的广泛关注[14-15],这项数值方法已经应用于各种电磁学问题如边界问题[16]、反向散射问题[17]、波导分析[18]。这种方法的优点是不需要对研究区域进行网格生成，而是采用空间节点离散处理的方法。这种方法对于分析复杂结构，例如非均匀材料和不连续结构等，具有非常好的效果,因此对于非均匀左手介质结构的数值分析具有天然的优势。

利用基于RBFs的无网格法分析非均匀左手介质时有两个问题需要注意。(1) RBFs形状参数的选取，采用唯一的形状参数，会导致特征值的求解精度极其依赖于配置点的位置，进而造成特征值精度的降低。因此本文采用具有特定统计分布的高斯型随机RBFs。(2) 采用点匹配技术分析非均匀介质时，会导致一个非对称的特征问题，造成特征方程求解困难。因此本文采用变分法和无网格法结合的方法得到对称的特征方程。

本文首次将基于RBFs的无网格法应用于非均匀左手介质填充波导特征值的计算中，并与解析法求得的精确结果和利用基于有限元法的电磁分析软件HFSS得到的仿真结果进行对比，验证了本文提出的无网格法在分析非均匀波导结构时的精确性和高效性。

1 数值方法及算法实现

1.1 场方程和基于径向基函数的无网格法

非均匀左手介质填充矩形波导的横截面面积A=a×b,Γ是矩形波导横截面的边界，该结构磁场H(x,y,z)的麦克斯韦方程组为：

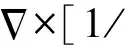
(1)

(4)

式中：ωpe和ωpm是等离子体频率；Γe和Γm是阻尼系数；h(x)和g(x)是非均匀介质的剖面函数，描述非均匀介质的非均匀特性。

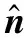
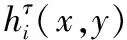
RBFs有各种类型，例如，高斯型、复二次函数型和反二次方程型，本方法采用文献[20]中定义的高斯型RBFs：

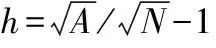
1.2 算法实现

利用基于RBFs的变分无网格法计算非均匀左手介质波导传播特性的算法流程如图1所示。本文算法由MATLAB编程实现。

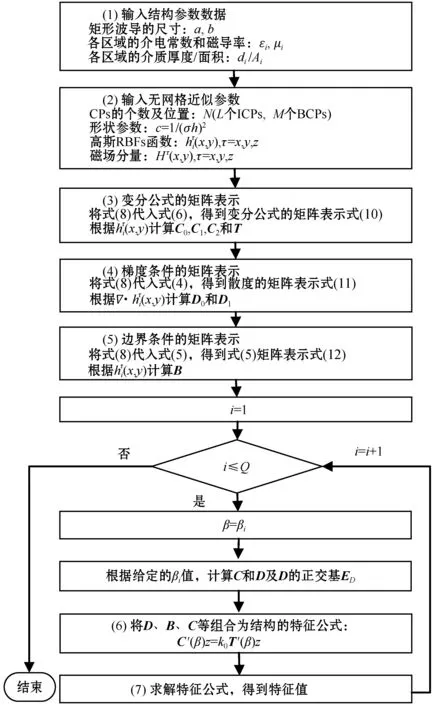
图1 基于RBFs无网格法的算法流程

步骤(1) 输入结构参数，包括波导的尺寸、波导中各非均匀区域的介电常数和磁导率，及各区域的厚度或面积。

步骤(2) 输入无网格法的相关参数，包括CPs的定义、形状参数的选取和RBFs函数的输入，根据以上参数计算得到的磁场分量Hτ(x,y)。

步骤(3)-步骤(5) 将Hτ(x,y)代入式(6)、式(4)及式(5)的矩阵表示，如式(9)-式(13)所示。

Da=0

(10)

Ba=0

(11)

其中：

C=C0+βC1+β2C2

(12)

D=D0+βD1

(13)

步骤(6)β-循环开始，计算β相关的矩阵C、D。之后，将式(9)-式(13)组合成特征方程，通过求解特征方程计算传播常数β，Q为β值的计算次数。β-循环停止即表示所有的β值已经求解完毕，对应的传播曲线绘制完成。

2 数值结果

本节利用基于径向基函数的变分无网格法计算了三种典型的非均匀左手介质填充矩形波导结构的传播特性。这三种结构在滤波器、耦合器、超材料特性的测量等方面都具有广泛的应用，而且这三种结构是规则填充的情况，因此可以求得解析解。本文的计算结果分别与解析解和HFSS的仿真结果进行对比，通过对比可以得到以下两点结论：

(1) 解析法得到的结果是特征值的精确解，因此与本文得到数值计算结果对比可以对无网格法的准确性和可行性进行分析。

(2) HFSS是目前最常用的基于有限元法的电磁数值分析工具，在相同精度要求下，对比无网格法和HFSS分析所需的时间，可以对无网格方法的效率进行分析。

这些结构作为微波电路的关键器件使用时，主要工作在主模式的状态下，而非均匀矩形波导的主模式是纵剖面电模式(longitudinal-section electric mode,LSE mode),因此本文主要对非均匀波导结构的LSEn0模式进行分析。

2.1 单层左手介质加载矩形波导

本文研究的第一个例子如图2所示，加载的左手介质将矩形波导分割为两个区域，区域I为真空区域，其中：εr1=1，μr1=1；区域II中左手介质的介电常数、磁导率和厚度分别为εr2=-4，μr2=-1及d2/d1=1/3。LSEn0模式的传播特性曲线如图2所示，其中：黑色实线代表解析法的计算结果；黑色方块代表无网格法的计算结果；黑色圆圈代表HFSS的仿真结果。该结构LSEn0模式的解析式为：

k2tan(k1d1)=-k1tan(k2d2)

(14)

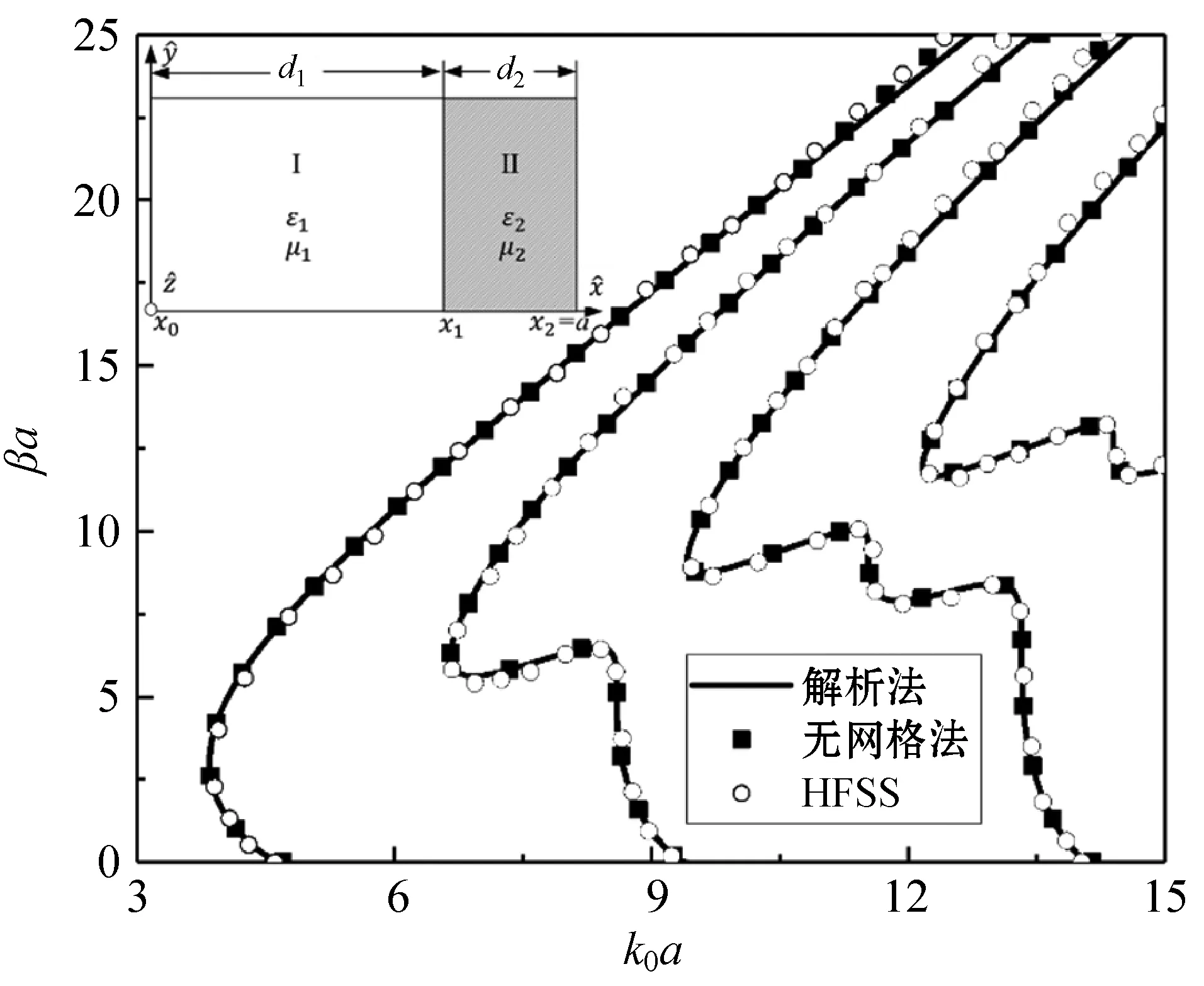
图2 单层左手介质加载矩形波导的传播特性曲线

利用式(14)可以求得该结构传播特性曲线的精确解。对于无网格法，CPs的数量为N=100，其中ICPs的数量为70，BCPs的数量为30，计算96个特征值的代码运行时间为6 s。作为对比，利用相同的工作站，HFSS仿真耗时接近3 min(180 s)。因此，相比于HFSS的分析时间，无网格法的数值分析效率非常高。图2中，无网格法的数值解、解析法的精确解和HFSS的仿真结果具有非常好的一致性，因此说明无网格法的准确性。

通过图2可以观察到，一些频段的群速度为负值(∂k0/∂β<0)，这与传统波导中正群速度(∂k0/∂β>0)的传播特性不同。在文献[4]中，将这种负群速度的传播特性称为“左手传播特性”。研究表明负群速度可能产生后向波传播特性，因此如果在图2所示的波导结构上适当开槽(slot)可以用作后向波辐射天线。

2.2 两层左手介质对称加载矩形波导

本文研究的第二个例子为如图3所示的两层左手介质对称加载矩形波导，其中区域I和区域III为左手介质(εr1=εr3=-4，μr1=μr3=-1，d1=d3=0.15a)，区域II为真空区域(εr2=1，μr2=1)。LSEn0模式的传播特性曲线如图3所示，其中:黑色实线代表解析法的计算结果；黑色方块代表无网格法的计算结果；黑色圆圈代表HFSS的仿真结果。该三层矩形波导结构的LSEn0模式的解析式为：

k2k3tank1d1+k1k3tank2d2+k1k2tank3d3-

利用式(15)可以求得传播特性曲线的精确解。对于无网格法，CPs数量为N=326，其中ICPs的数量为282,BCPs的数量为44。计算87个特征值的代码运行时间为8 s。作为对比，利用相同的工作站分析同样的三层波导结构，HFSS仿真时长接近5 min(300 s)。图3中，无网格法的数值解、解析法的精确解和HFSS的仿真结果具有非常好的一致性，说明无网格法分析该三层结构的准确性。

图3 两层相同的左手介质对称加载矩形波导的传播特性曲线

2.3 单层左手介质中心填充矩形波导

本文研究的第三个例子是对如图4所示的单层左手介质中心填充矩形波导进行分析。填充的左手介质将矩形波导分割为3个区域，其中区域II为左手介质(εr2=-4，μr2=-1，d2=0.4a)，区域I和区域III为真空区域(εr1=εr3=1，μr1=μr3=1)。LSEn0模式的传播特性曲线如图4所示，其中：黑色实线代表解析法的计算结果；黑色方块代表无网格法的计算结果；黑色圆圈代表HFSS的仿真结果。其中变分无网格法的CPs设定与2.2节中的设定相同，即CPs数量为N=326，ICPs的数量为282,BCPs的数量为44，而三层介质填充波导的特征方程依然为式(15)。计算79个特征值的代码运行时间为6.5 s。作为对比，利用相同的工作站分析同样的中心填充波导结构，HFSS仿真时长接近5 min(300 s)。图4中，无网格法的数值解、解析法的精确解和HFSS的仿真结果具有非常好的一致性。在这种结构中在某些频段中可以观察到负群速度的“左手传播特性”。

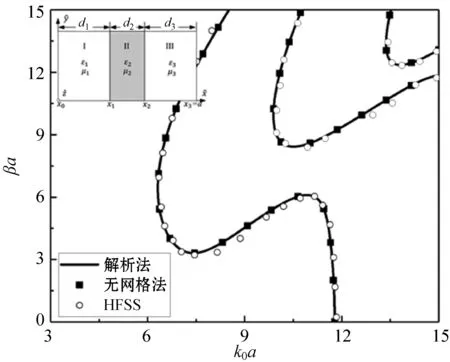
图4 一层左手介质中心填充矩形波导的传播特性曲线

3 结 语

本文将基于径向基函数的变分无网格方法推广到非均匀左手介质填充波导的数值计算中，这种方法的优势在于无须对研究区域进行网格生成，大大节省了计算和存储资源。特别是在包含非均匀介质、尖角及突变的复杂结构的分析中，无须对复杂区域进行额外的高质量高密度的网格划分。因此该方法尤其适用于非均匀介质和不连续结构的数值分析。本文详细地分析了三种具有代表性的非均匀左手介质波导结构，并且将无网格法得到的结果分别与精确的解析解和有限元法的仿真结果进行对比，说明无网格法在分析非均匀左手介质填充波导时具有精确度高和计算时间短的优点。分析结果得出，部分填充左手介质的矩形波导在某些频段支持具有负群速度的后向波传播模式(左手传播模式)，为具有后向波辐射天线的设计提供了一种新结构。

在之后的研究中，计划利用无网格法分析更加复杂的波导结构，例如近年提出的基片集成波导结构(SIW)和悬置微带线结构等。此外，也计划利用该方法分析更加多样的新型介质。本文研究的左手介质是一种新型的人工电磁介质，而近年来各种各样的人工电磁介质层出不穷，例如具有渐变折射率的人工电磁媒质、具有各种特性的光子晶体等，这些介质及含有这些介质波导的分析同样需要准确的数值计算方法。因此，本文提出的无网格法为复杂波导和新型介质的数值分析提供一种高效而精确的方法。