等温剩磁曲线分解方法及其批量处理工具BatchUnMix

白帆，常燎,2*，薛鹏飞，汪诗舜

1 北京大学地球与空间科学学院造山带与地壳演化教育部重点实验室，北京 100871 2 青岛海洋科学与技术试点国家实验室海洋地质过程与环境功能实验室，青岛 266071

0 引言

环境磁学通过研究天然样品的磁学性质，用于示踪不同环境、地质和地球物理过程（例如，潘永信和朱日祥，1996；王喜生等，2006；邓成龙等，2007；Liu et al.,2012）.环境磁学研究大多数是利用全岩磁学参数（bulk magnetic parameters）来表征样品中所有磁性矿物的综合响应，然而天然样品中的磁性矿物组分通常高度不均一，含有不同矿物类型、形态粒度、化学状态、以及微观结构的磁性矿物集合体，使宏观磁学参数的解释具有不确定性与复杂性，因此，分离并提取不同磁性组分信息对于提升环境磁学方法的探测精度和可信度尤为重要（Heslop,2015）.磁性组分是指具有相同矿物学或者相似物理性质（例如颗粒尺寸、形态、结晶度等）的磁性颗粒集合（Egli,2003）.目前广泛使用的分离磁性组分的岩石磁学方法包括测量并分析样品的磁滞回线（Heslop,2015）、磁化率-温度曲线（Liu et al.,2012）、剩磁曲线（Egli,2003,2004a,b）以及一阶反转曲线（Roberts et al.,2000,2014；秦华峰，2008）等.这些方法的广泛应用极大地帮助了人们对自然环境中磁性矿物的形成、搬运、沉积和转化等过程的理解.在这些方法中，由于测量等温剩磁（isothermal remanent magnetization；IRM）曲线对样品无损且高效简便，所以IRM曲线分解成为目前分离磁性矿物组分最常用的方法之一.IRM曲线根据其获得方式一般分为IRM获得曲线和反向场退磁曲线（Egli,2003）.IRM获得曲线测量方式为将退磁后的样品置于逐渐增大的外磁场中，外磁场每增大一步后将其撤去，然后测量样品的剩磁.IRM反向场退磁曲线的测量方式为先将样品沿着正向外磁场方向饱和，然后施加逐渐增大的反向磁场，测量样品在撤去外磁场后的剩磁.

本文首先从数学模型的角度综述了近年来提出的IRM曲线分解方法，然后重点介绍我们基于MATLAB开发的GUI工具BatchUnMix，并利用实验数据展示和评估了BatchUnMix处理天然样品IRM曲线的实用性，最后讨论了IRM曲线分解方法的局限性并提出了相关方面有待进一步研究的科学问题.

1 参数化方法

1.1 累积对数高斯函数

Robertson和France（1994）通过分析磁赤铁矿、赤铁矿和针铁矿样品的IRM获得曲线发现，单一磁性矿物的IRM获得曲线形态可以用累积对数高斯（cumulative log-Gaussian,CLG）分布进行拟合：

（1）

其中，B为磁性矿物获取剩磁时施加的外磁场大小；B1/2为平均剩磁矫顽力，为磁性矿物获得半饱和剩磁（SIRM）时的外磁场大小；DP（dispersion parameter）为离散参数，对应于对数-高斯函数的一个标准差；Mr为该单一磁性组分的饱和剩磁.Robertson和France（1994）进一步的研究表明，磁性矿物颗粒间不存在静磁相互作用的情况下，N种矿物混合后的IRM获得曲线是每种矿物所对应的IRM获得曲线的线性叠加，即可以用每种矿物对应的CLG函数之和拟合磁性矿物混合后的IRM获得曲线，对应的方程为

（2）

其中i表示第i个磁性成分.

Eyre（1996）和McIntosh等（1996）在研究中国黄土时采用了上述分析方法，利用对数高斯概率密度函数拟合样品中每个磁性组分的IRM获得曲线的一阶导数曲线，从而得到样品的矫顽力分布.然而在拟合IRM曲线的过程中，他们对磁性组分的数目及拟合效果的好坏是通过直接观察判断的，存在很大程度的主观因素.此后，Stockhausen（1998）提出使用三个基于残差平方和（RSS）的参数来判断IRM曲线拟合优度，并用FORTRAN语言编写了拟合程序，但他并没有给出何时使用这三个参数的标准.

Kruiver等（2001）基于前人提出的累积对数高斯分布及对数高斯概率密度分布的拟合方法，又提出了用正态分布的标准分数（Z分数）表示每个磁性组分的IRM曲线，称其为标准获得曲线（standardised acquisition plot,SAP；图1c）.如果样品只含有一个磁性组分，那么其IRM曲线的SAP为一条直线.如果样品含有多个磁性组分，那么其IRM曲线的SAP为各个磁性组分的SAP叠加，会呈现出曲线的形态.例如，当样品中存在赤铁矿等高矫顽力磁性组分时，其IRM曲线的SAP高场部分会有明显的弯曲（例如，Abrajevitch et al.,2009）.结合IRM获得曲线（也被称为线性获得曲线，LAP；图1a）、标准获得曲线（SAP；图1c）及IRM一阶导数曲线（也被称为梯度曲线，gradient of acquisition plot，GAP；图1b），可以利用不同数量的CLG曲线，通过调整它们各自的log（B1/2）、DP和Mr参数对IRM曲线进行组分分析（Kruiver et al.,2001）.对于拟合过程中存在的多解性问题，例如可以用不同数目的磁性组分拟合剩磁曲线，他们通过对不同拟合结果与原始数据的残差平方和（RSS）进行F检验和t检验来判断两个模型是否存在显著差异，从而得到最优拟合参数.基于以上方法开发的EXCEL工具IRM-CLG已在古地磁学及环境磁学研究得到了广泛使用（Yamazaki and Ikehara,2012；Hu et al.,2013；Chang et al.,2014,2018；Abrajevitch et al.,2015；Wang et al.,2019；Xue et al.,2019）.

Stockhausen（1998）和Kruiver等（2001）提出的方法都需要不断手动调节每个磁性组分IRM曲线的拟合参数（log（B1/2）、DP和Mr）.当样品的组分较为复杂时，例如当样品中包含四个磁性组分，需要调节的拟合参数多达12个，此时拟合一个样品的IRM曲线需要花费较长时间.Heslop等（2002）提出了基于对数似然和期望最大化算法（Dempster et al.,1977）自动寻找拟合IRM一阶导数曲线所需最优参数的方法，并用FORTRAN语言编写了相应程序.当原始数据存在较大噪声时，首先要对数据进行三次样条平滑，再开始进行拟合.拟合过程包括求期望（E步骤）和最大化对数似然函数（M步骤）两步：E步骤，根据初始化拟合参数或M步骤中产生的参数计算完整数据对数似然函数的期望；M步骤，最大化E步骤中的对数似然函数的期望产生新的拟合参数值.经过不断迭代，最终收敛并得到最佳拟合结果.该方法的最后结果与初始值无关，只需要给定磁组分数目即可自动拟合，提高了IRM曲线分解的效率并得到较为客观的拟合值，有较为普遍的使用（Roberts et al.,2012；Dorfman et al.,2015；Li et al.,2020）.然而，由于该方法无法对样品的先验地质背景信息加以约束限定，所以在对最终拟合结果进行解译时需仔细推敲其物理或地质意义.

1.2 偏态广义高斯分布函数

随着对数高斯分布拟合IRM曲线方法的应用和发展，Heslop等（2004）发现磁性矿物间的静磁相互作用和热弛豫会使得一些磁组分的矫顽力分布呈现出偏离CLG函数的偏态分布.鉴于此，Egli（2003）提出使用偏态广义高斯分布（skewed generalized Gaussian,SGG）函数对磁性组分进行拟合.SGG函数除了包含CLG函数的B1/2、DP和Mr三个参数外，还另外包含了偏度和峰度两个参数，SGG函数的概率密度函数为（图2）：

图1 IRM获得曲线在纵坐标为线性，梯度及概率尺度的表现形式（a—c） 分别为线性获得曲线图，获得曲线梯度图，和标准获得曲线图.改自Kruiver等（2001）.Fig.1 IRM acquisition curve on linear,gradient,and probability scale（a—c） are linear acquisition plot （LAP）,gradient of acquisition plot （GAP）,and standardised acquisition plot （SAP）,respectively.Modified from Kruiver et al.（2001）.

（3）

Egli（2004a）通过分析大量天然样品的IRM曲线分解结果发现，SGG函数中偏度参数对拟合结果的影响远比峰度参数显著，在p=2的情况下，通过调节方程（3）中的偏度参数就可以得到理想的拟合结果.鉴于此，Maxbauer等（2016）提出，可以使用偏斜正态（skew-normal distribution）分布拟合IRM曲线，偏斜正态函数中没有引入峰度参数p，而是在正态函数基础上引入了控制偏度的参数（s），s=0时，蜕变为正态函数.Maxbauer等（2016）发布了基于R语言编写的网页应用程序MAX UnMix，该程序提供了图形化用户界面，操作便捷.使用时，用户需首先确定磁性组分的数目，并赋予每个磁性组分B1/2、DP、p和偏度参数s的初始猜想值（p为磁性组分对样品磁性的贡献），然后应用程序基于这些初始值通过不断迭代减小拟合模型和原始数据的RSS以得到最佳拟合结果.需要指出的是，MAX UnMix仍对IRM曲线的一阶导数数据进行拟合，因此如果原始数据信噪比低，可以用该程序提供的样条平滑功能进行降噪.由于MAX UnMix是网页应用程序，访问便捷，同时拟合方法相较于Egli（2003）减少了对峰度参数的调节从而提高了拟合效率，逐渐成为IRM数据磁组分分析的热门选择（Maxbauer et al.,2017；Font et al.,2018；Chang et al.,2019；Abrajevitch,2020；He et al.,2020；Usui and Yamazaki,2021；Wang et al.,2021；Xue et al.,2022）.

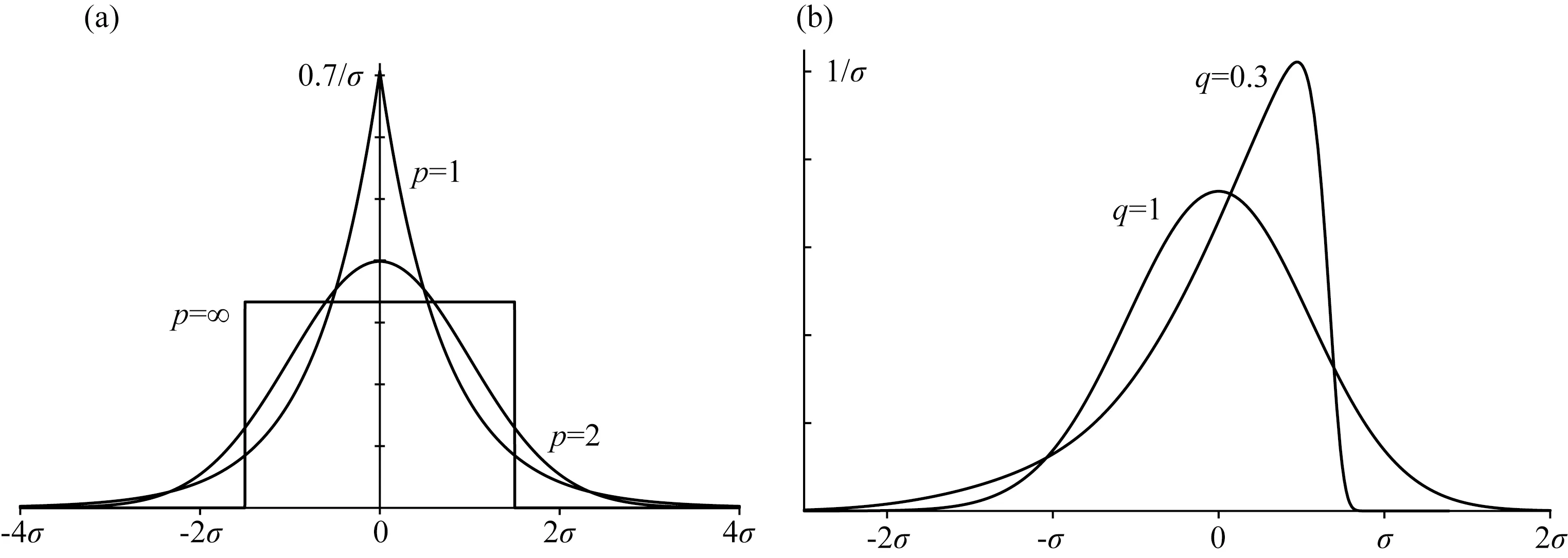
图2 偏态广义高斯分布示意图（a） μ=0，σ=1，且q=1时的SGG分布.p=1为拉普拉斯分布，p=2为高斯分布，p=∞时为箱形分布；（b） 左偏SGG分布，μ=0，σ=0.5485.改自Egli（2003）.Fig.2 Examples of SGG distributions（a） SGG distribution with μ=0,σ=1,and q=1.p=1 for a Laplace distribution,p=2 for a Gauss distribution;（b） Left-skewed SGG distributions with μ=0 and σ=0.5485.Modified from Egli （2003）.

1.3 Burr Ⅻ 分布

Zhao等（2018）提出使用12种Burr分布（Burr,1942）类型之一的Burr Ⅻ 分布的累积分布函数拟合样品的矫顽力分布（图3）.与SGG和偏斜正态分布相似，Burr XII分布具有丰富的分布形态；不同的是，其累积分布具有解析的表达形式，因此可以直接对IRM原始数据进行拟合，能避免对原始数据差分而放大噪音.Burr Ⅻ 分布的累计分布函数和概率密度函数分别为

α>0,γ>0,λ>0，

（4）

α>0,γ>0,λ>0，

（5）

其中，B代表磁场强度，λ是与函数分布宽度有关的参数，分布的形状由参数α和γ共同决定.当γ>1的时候，分布是单峰的，α或λ的增大会导致分布变窄.当使用该分布拟合具有多个磁性组分的样品时，累积分布函数的形式为

（6）

每个磁性组分由四个参数加以描述：磁性组分对样品磁性的贡献ci、尺度参数λi以及形状参数（αi和γi）.

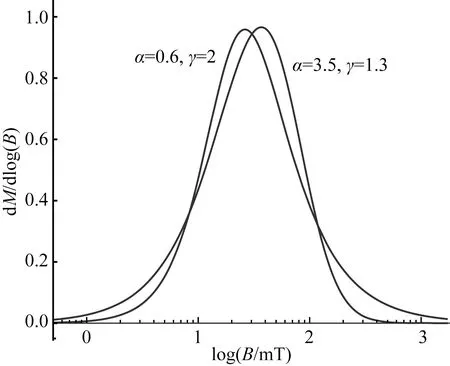
图3 Burr Ⅻ 分布示意图（改自Zhao et al.，2018）Fig.3 Example of Burr Ⅻ （modified from Zhao et al.,2018）

对于磁性组分数目的选择，Zhao等（2018）采用了赤池信息量准则（Akaike information criterion,AIC；Akaike,1998），提供了权衡拟合模型复杂度（即磁性组分数目）和拟合优度的标准.AIC方程为

=2k+NlnRSS+C，

（7）

相较于前人提出的需要给定参数初始猜想值的拟合策略（Kruiver et al.,2001；Egli,2003；Maxbauer et al.,2016），Zhao等（2018）根据磁性组分的数目设定参数范围，然后在该范围内自动随机选取参数值，找到使得拟合数据和原始数据的RSS最小的参数值作为最佳拟合参数.该策略提高了拟合效率并且降低了人为给定参数初始猜想值的主观影响.He 等（2020）进一步优化了该方法的拟合策略.他们首先对原始数据点进行多次重采样（重采样点数为原始数据点的80%），对每次重采样的数据用Zhao等（2018）提出的方法进行处理后得到磁性组分数目和拟合参数的估计值，从中选取使得AIC最小的估计值作为相关参数的初始猜想值进行优化拟合，得到最佳拟合参数及其置信区间.该策略对减少原始数据中的噪声影响有一定帮助.

2 非参数化方法

Heslop和Dillon（2007）提出使用非负矩阵分解算法（non-negative matrix factorization,NMF；Lee and Seung,1999）分解一组样品的IRM获得曲线以进行端元组分分析的方法.运用非负矩阵是因为从物理角度来说，IRM获得曲线随外磁场变化增大或不变，如果没有该物理约束，数学上求解时由于测量误差和噪音等原因会出现与实际不符的负端元组分.该方法不依赖于任何分布函数，仅使用端元组分的线性叠加表示每个样品的IRM获得曲线.非负矩阵为

X=AS+ε，

（8）

矩阵A代表贡献矩阵，大小为n行m列（n为样品数目，m为端元组分数目），每行为m个端元组分对每个样品IRM获得曲线的贡献；矩阵S代表端元组分的IRM获得曲线矩阵，大小为m行l列（m为端元组分数目，l为外磁场强度变化步骤数目），每行为每个端元组分剩磁随外磁场变化的大小，即该端元组分归一化后的IRM获得曲线；矩阵X为对n个样品测量得到的IRM获得曲线矩阵，大小为n行l列，每行对应于每个样品在每步外磁场下测量得到的剩磁.ε为测量误差或其他情况对矩阵X的影响，例如静磁相互作用.

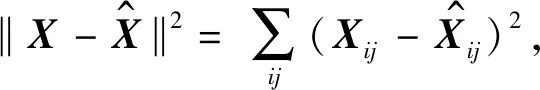
（9）

（10）

其中i、a、μ是矩阵A和S的索引，i从1到n，a从1到m，μ从1到l.

分解矩阵X前如果数据存在较大的噪声，先用三次样条法平滑数据再进行求解.求解时首先需要给定矩阵A和S的初始猜想值以及端元组分的数目（m）.矩阵S的初始猜想值用对矩阵X的模糊c-均值聚类给出，矩阵A的初始猜想值根据非负最小二乘法得到（Lawson and Hanson,1974）.端元组分数目由每步外磁场上的X和AS之间的确定系数R2的大小来判断，随着端元组分数目的增多，R2随之增大而后趋于平缓，一般选择其拐点位置所对应的端元组分数目.然后将这些初始化的值其代入方程（9）和（10）中进行迭代即可得到矩阵A和S的解.

Heslop和Dillon（2007）提出的NMF分解法可以快速求解多个相似样品IRM获得曲线的端元组分，是分析复杂样品的有力工具（Dekkers,2012；Just et al.,2012）.然而，该方法对求解过程没有任何约束且解不具有唯一性，所以需要结合样品的地质背景对端元组分进行谨慎判断.该方法要求原始数据中的每条IRM获得曲线单调递增，每条曲线有相同数目的数据点且外磁场步长一致，所以有时需要对原始数据进行预处理，例如插值等.这在一定程度上限制了使用此方法的便捷性.此外，Heslop和Dillon（2007）建议矩阵X最少应包含50个样品的剩磁曲线以保证结果的可靠性.

3 BatchUnMix

CLG函数作为拟合IRM曲线的最常用函数之一，发布的EXCEL版（Kruiver et al.,2001）数据分析工具为研究人员提供了很大便利.然而，Kruiver等（2001）提出的拟合策略需要提供拟合参数的初始猜想值，并且需要不断手动调节拟合参数值以找到最佳拟合效果，这使得IRM曲线处理效率不高且结果受到人为主观因素的影响，鉴于此，我们开发了基于MATLAB的GUI工具BatchUnMix，以实现对IRM数据批量拟合，优化IRM曲线分解策略的基础上提高处理效率，以及增强拟合结果的客观性.

3.1 方法描述

BatchUnMix采用了CLG函数模型（Robertson and France,1994），对归一化后的IRM一阶导数曲线进行分解.拟合参数为log（B1/2）、DP和C，其中C为磁性组分对样品磁性的贡献.拟合使用了MATLAB拟合工具箱（curve fitting toolbox）中的高斯拟合函数，其表达式如方程（11）所示：

（11）

其中i表示第i个高斯组分，参数与方程（1）中的拟合磁性组分参数对应关系为

Bcr=bi，

（12）

（13）

（14）

最佳拟合参数采用非线性最小二乘法在一定的参数范围内自动寻找得到.我们参考Egli（2004a）对大量沉积物样品IRM曲线的拟合结果以及一些已发表文献中样品的IRM曲线拟合结果，在BatchUnMix中设置了默认的log（B1/2）和DP的大致范围，log（B1/2）的范围为0～3，DP的范围为0～0.6.但是仍然建议用户根据对具体样品中磁性矿物组分的先验地质背景知识设置参数范围，否则有可能得到数学上的最优解，但却不符合样品所含磁性组分的真实情况.拟合参数和原始数据的95%置信区间使用自展法（bootstrap）对原始数据进行100次重采样得到.每次采样中假设参数的误差为正态分布，置信区间为2%，以此计算该次采样的最佳拟合参数.如果原始数据存在较大噪声，采用滑动平均法对其进行降噪处理.滑动平均法是将数据中某点附近的N个采样点的（N为奇数）算数平均作为该点平滑后的值.相比于前人采用的三次样条降噪，滑动平均法的数学原理较为简单，平滑参数的选取也仅限于整数，降低了用户的使用难度，可以让用户对曲线平滑有更好的把握.而三次样条降噪的平滑参数选取较难把握，比较容易过度平滑原始数据而丢失关键信号，或者平滑数据不到位使噪声依然对分解结果产生影响.需要指出的是，三次样条法和滑动平均法都是常见的降噪方法，这两种方法对于有噪音的IRM数据都有较好的平滑效果，但都存在当噪音较强时，无法很好将噪音和真实信号分开的缺点.

BatchUnMix的主要运行窗口如图4所示，处理IRM曲线的主要流程为（图5）：（1）选择处理数据方式及数据格式：单个文件处理或者批量处理；振动样品磁强计（VSM）测量文件格式或包含外磁场和剩磁信息的xlsx.格式文件；剩磁获得曲线或者反向场退磁曲线；是否对拟合参数和原始数据求取置信区间（图4a）；（2）选择输入文件，根据原始数据和数据的一阶导数图判断是否需要对数据进行平滑；（3）选择拟合所需磁性组分的数目，然后对参数（log（B1/2）、DP和C）的范围进行设置并开始拟合（图4b）；（4）根据得到的结果判断是否需要返回上步重新调节参数范围再次拟合（图4c）；（5）最终结果自动保存为fig.格式图片和xlsx.格式文件.

3.2 BatchUnMix拟合示例及拟合结果比较

我们用BatchUnMix对典型沉积物及火成岩样品的IRM数据分别进行了单样品处理和批量处理，并将拟合结果和已发表的使用MAX UnMix（Maxbauer et al.,2016）分析结果进行了比较.分析使用的沉积物样品来自国际大洋发现计划（IODP）位于北大西洋的U1403B钻孔（Xue et al.,2022），火成岩样品组来自中国大洋航次西南印度洋中脊采集的40块玄武岩样品（Wang et al.,2021）.这两组样品的磁性组分鉴定有电子显微直接观测结果的约束——U1403B钻孔中的磁性矿物组成为碎屑磁铁矿与软磁及硬磁性生物磁铁矿（Xue et al.,2022），西南印度洋中脊玄武岩中的磁性矿物组为微米级钛磁铁矿枝晶与纳米级钛磁铁矿包裹体（Wang et al.,2021）.沉积物中的生物磁铁矿具有指示深海环境意义（Chang et al.,2018），而洋中脊玄武岩是了解洋脊磁异常机理和洋壳水岩相互作用等科学问题的重要介质（刘隆等，2021；Wang et al.,2021），所以选用这两类样品展示BatchUnMix拟合效果并与已有结果对比.

3.2.1 单样品处理

对于U1403B沉积物样品，参考Xue等（2022）的拟合结果，首先确定用四个磁性组分拟合IRM一阶导数曲线，然后我们使用了不同的参数设置方式以对比分析：（1）设置三个组分的log（B1/2）范围分别为：1.4～1.5，1.7～1.8和2.3～2.6，其他参数为默认范围；（2）只设置高场成分的log（B1/2）范围为2～3，其他参数为默认范围.这两种拟合方式得到了相似的结果（图6b,c）：包含两个狭窄的矫顽力分布（较小的DP）以及另外两个低场和高场组分，显示了和Xue等（2022）拟合结果的一致性（图6a；表1）.Xue等（2022）结合透射电镜数据，将拟合结果解释为生物成因软磁组分（biogenic soft,BS）和生物成因硬磁组分（biogenic hard,BH），是沉积物中磁铁矿化石磁小体的典型特征（Egli,2004a），其余两个磁性组分分别对应低矫顽力的碎屑磁铁矿和高矫顽力的赤铁矿.

图4 BatchUnMix程序主要运行窗口截图（a） 数据选择窗口；（b） 参数设置窗口；（c） 拟合结果窗口.Fig.4 Screenshots of main user interface of program BatchUnMix（a） Data selection window;（b） Parameter setting window;（c） Fitting result window.

该示例表明，当具备对样品所含磁性组分的先验知识时，可以仅对较为确定的磁性组分参数范围进行设置（图6c），其他参数范围保持默认设置，所得到的拟合结果和对参数范围进行精细设置的结果相差不大（图6b）.

3.2.2 样品批量处理

我们对于40块西南印度洋中脊玄武岩样品的IRM一阶导数曲线分为两种情况进行批量处理：（1）同时设置log（B1/2）和DP范围，（2）只设置log（B1/2）范围.然后将拟合得到的磁性组分参数进行了100次迭代的K均值聚类分析，并与Wang 等（2021）的统计结果进行了比较.情况（1）得到了和Wang等（2021）相似的统计结果（图7a,b）.情况（2）虽然得到了和图7a，b相似的聚类中心（图7c），但两个聚类中心重合度较高.这是由于相比使用MAX UnMix和情况（1）处理的IRM曲线（例如，图7d,e），当参数设置为情况（2）时，部分IRM曲线的拟合结果并没有得到更符合真实的组分（图7f）.

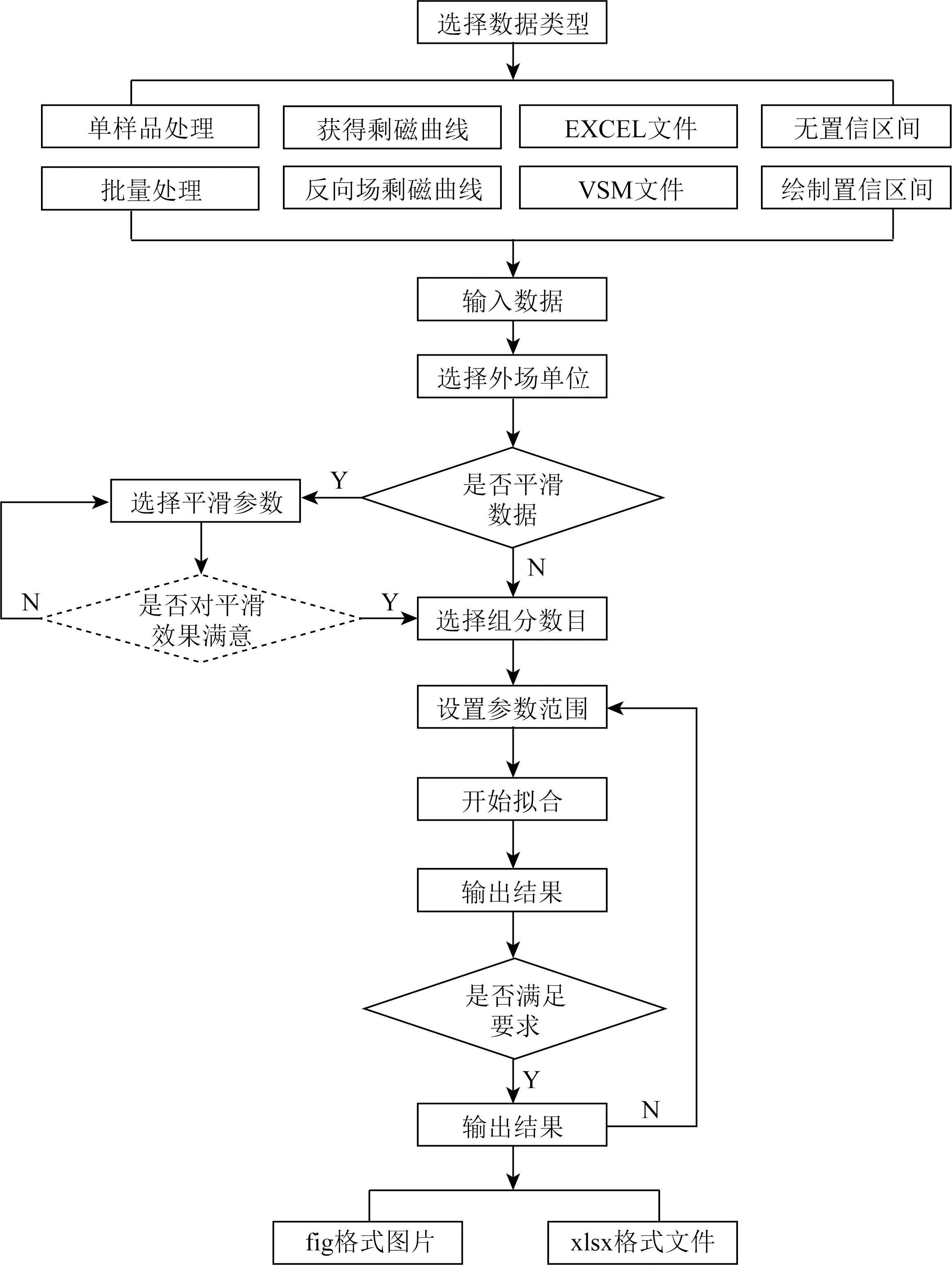
图5 BatchUnMix操作流程图.虚线框表示该功能仅在处理单个样品中具备Fig.5 Procedures of data analysis in BatchUnMix.Dotted boxes indicate that the function is only applicable for single sample processing

表1 使用MAX UnMix和BatchUnMix处理北大西洋沉积物样品结果（BatchUnMix采用了两种参数设置）Table 1 Results of decomposing IRM curves for a sediment sample from the North Atlantic using MAX UnMix and BatchUnMix,respectively （BatchUnMix uses two different parameter settings）

图6 对比不同分解方法及BatchUnMix不同参数设置下处理北大西洋深海沉积物样品的同一IRM数据示例（a） 使用MAX UnMix（Maxbauer et al.,2016）的处理结果（改自Xue et al.,2022）；（b,c） 使用BatchUnMix在不同参数设置情况下的处理结果.Fig.6 Examples of decomposing IRM curves with different methods and parameter settings in BatchUnMix for the same IRM dataset of a North Atlantic pelagic sediment sample（a） shows result using MAX UnMix modified from Xue et al.（2022）;（b,c） are results using BatchUnMix with two different parameter settings （see text）.

结合本例及对其他样品已发表数据批量处理的测试，我们发现批处理过程对参数范围设置精细度要求较高.所以建议在批量处理数据前，先随机挑选部分样品对其剩磁曲线进行单独拟合，得到相关磁性组分参数的大致范围，由部分估计整体，再进行批量拟合.此外，批量处理一般较适用于所含磁性组分相似的样品，当样品间磁性特征相差较大时，可能得不到真实解.

4 IRM曲线分解方法的局限性

尽管拟合IRM曲线的函数模型和分解策略经过了几十年的发展逐渐完善，但使用IRM曲线分解方法开展磁性组分分析仍然存在一定的局限性.

首先，IRM曲线的分解结果具有多解性.同一样品的IRM曲线分解时，在满足数学上的拟合优度后，可能有不同的分解结果.例如，图8a展示了对来自孟加拉湾沉积物样品的IRM曲线分解后的两种不同结果，结合该样品的电镜照片（Xue et al.,2019），这两种拟合结果都有一定的合理性，都可以解释为不同粒度的磁铁矿导致的两种不同的磁性组分.SGG函数和Burr Ⅻ分布具有高度灵活的特点，所以它们相对于CLG函数多解性问题更为突出（Zhao et al.,2018）.此外，当样品的IRM曲线可以由不同数目的磁性组分拟合时，增加磁性组分数目通常会提高拟合优度，但是得到的磁性组分可能不具有真实物理意义.此时，结合Heslop和Dillon（2007）提出的非参数化方法对样品的IRM曲线进行磁性组分分析可以对磁性组分数目的选择起到一定的帮助（Wang and Chang,2022）.

IRM曲线分解结果对拟合函数模型的选取有一定的依赖性（Egli,2003;Zhao et al.,2018），只有选取与样品中的真实组分最接近的函数模型，才能更好的重建组分信息.图8b展示了对合成磁铁矿样品IRM曲线拟合时，用CLG函数、Burr Ⅻ分布和SGG函数分别对其分解后得到了不同的结果（Zhao et al.,2018）.此外，Egli（2003）中的图10展示了存在使用一个SGG组分拟合IRM曲线的效果和使用两个对数正态分布组分拟合IRM曲线的效果相似的情况.所以，当使用不同函数模型拟合IRM曲线后得到差异较大的结果时，建议研究人员改变拟合参数对样品的IRM曲线重新进行拟合，或者结合该样品的其他岩石磁学数据对拟合函数模型做出选择.

此外，样品中同一物理组分可能需要用多个数学组分描述（He et al.,2020;Bai et al.,2021）.例如，单一尺寸分布的磁铁矿颗粒集合体，如果颗粒间存在较强的相互作用，那么拟合其IRM曲线需要两个数学组分（Bai et al.,2021）.噪声也会对IRM曲线的分解结果有一定的影响（Zhao et al.,2018），CLG函数相比于SGG、skew-normal、Burr Ⅻ分布有较少的拟合参数，所以对噪声的敏感度更低.对于有噪声的IRM数据，除了对其进行平滑外，可以使用拟合函数的cumulative distribution function（CDF）和probability distribution function（PDF）对IRM曲线分别进行拟合并比较结果，Zhao等（2018）的研究指出，IRM原始数据与其一阶导数曲线有不同的噪声敏感度，所以用拟合函数模型的CDF拟合IRM原始数据和PDF拟合IRM一阶导数曲线就数据噪声而言可以视为两种独立的拟合IRM曲线方法.

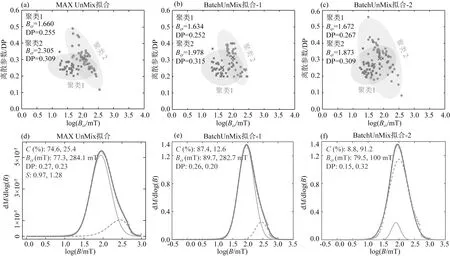
图7 对比不同IRM曲线分解方法及BatchUnMix不同参数设置下处理西南印度洋中脊玄武岩同一组IRM数据示例（a—c）对40块样品批量处理后再进行K均值聚类分析结果；（a） 使用MAX UnMix（Maxbauer et al.,2016）处理的结果，改自Wang等（2021）；（b） 在BatchUnMix中同时设置log（B1/2）和DP范围时的处理结果；（c） 在BatchUnMix中只设置log（B1/2）范围时的处理结果；（d—f） 分别对应图（a—c）批量处理中的单样品处理结果示例.Fig.7 Examples of decomposing the same IRM dataset with different methods and parameter settings in BatchUnMix for basalt samples from the Southwest Indian Ridge（a—c） show results of K-means clustering analysis for unmixed IRM components of 40 basalt samples;（a） Result using MAX UnMix,data modified from Wang et al.（2021）;（b） Data processed using BatchUnMix with setting log（B1/2） and DP ranges simultaneously;（c） Data processed using BatchUnMix with only setting log （B1/2） ranges;（d—f） show examples of IRM fitting for single sample from results in （a—c）,respectively.

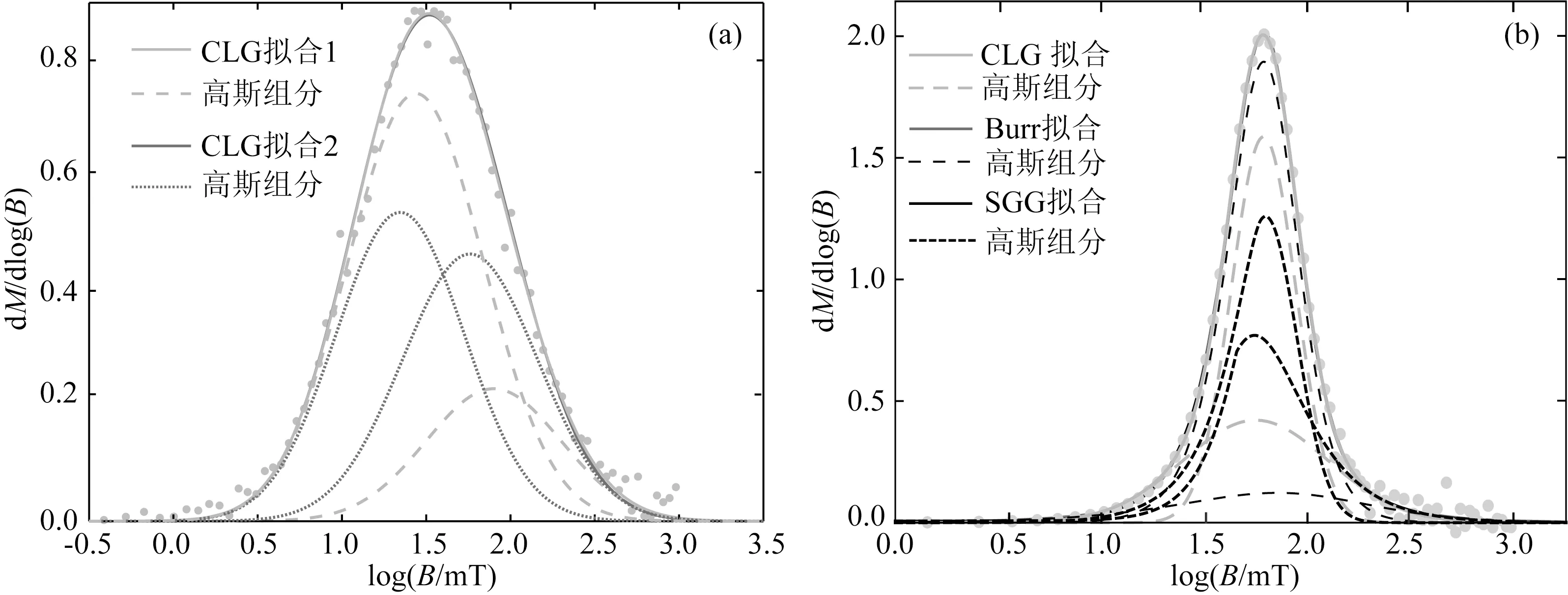
图8 IRM曲线分解的多解性及模型依赖性示例（a） CLG函数分解IRM曲线多解性示例；样品为孟加拉湾表层沉积物（Xue et al.,2019）；（b） IRM曲线分解模型依赖性示例（改绘自 Zhao et al.,2018）.Fig.8 Examples of multiplicity and model dependency for IRM curve decomposition（a） Example of multiplicity for IRM curve decomposition for surface sediment sample from the central Bengal Fan （Xue et al.,2019）;（b） Example of model dependency for IRM curve decomposition.

鉴于上述提到的IRM曲线分解方法存在的局限性，在处理样品的IRM曲线时，需要具备对样品的先验判断，并结合其他磁性参数，例如磁滞回线、一阶反转曲线等，以及运用电镜矿物成像等方法进行综合分析判断.单一对IRM曲线进行磁组分分析往往不能完全清楚地揭示复杂样品的磁性组分信息.

近年来微磁模拟的快速发展为建立磁性组分与样品真实组分的可靠联系提供了一种有效方法（Bai et al.,2021,2022）.微磁模拟可以分别评估磁性矿物的粒度、形态及彼此间存在的静磁相互作用等对IRM曲线分解的影响，从而为分离的磁组分解释提供可靠的理论支撑.例如，Bai等（2021）使用微磁模拟的方法系统研究了不同形状（拉长和扁平球体、正方体和八面体）和空间分布（不同颗粒间距）的磁铁矿颗粒集合体对IRM曲线形状的影响.研究表明，对于拉长颗粒集合体，即使集合体内的颗粒粒度分布单一，颗粒间的静磁相互作用也会导致其IRM曲线分解得到的高斯组分与富含生物磁小体化石的沉积物磁组分分析结果相似.

5 小结与展望

本文系统回顾了IRM曲线分解方法，并基于CLG函数提出了新的IRM曲线分解MATLAB工具BatchUnMix（下载地址：https:∥doi.org/10.18170/DVN/RVQGLE），该工具加入了批量处理功能，通过设定部分拟合参数的范围自动寻找其最优解，降低了人为给定拟合参数初始猜想值的主观性影响，并显著提高了IRM数据处理效率.

虽然IRM曲线分解是鉴别样品中磁性矿物组分的有力方法，然而其本身存在的局限性使得研究人员在使用该方法时需格外谨慎.未来应对影响IRM曲线分解的因素进行更为深入的研究，例如使用微磁模拟的方法，以构建起数学解和真实解之间的桥梁，从而更为清楚准确地解译样品中所含磁性组分的信息.

致谢感谢北京大学的Thomas Berndt博士、澳大利亚国立大学的赵翔博士、上海交通大学的赵翔宇博士的有益讨论.感谢中国海洋大学的姜兆霞教授和另一位匿名审稿人的建议使本文获得了提升.