基于扰动观测器的永磁同步风力发电机无速度传感器控制

郭磊磊，朱林强，曹玲芝，李琰琰，王朋帅

（郑州轻工业大学电气信息工程学院，河南 郑州 450002）

近年来，气候变暖、温室效应等气候问题接踵而来，环境问题愈发受到各国关注，清洁能源的研究与应用逐渐登上世界舞台。在众多的清洁能源中，风能更具有应用价值。随着各国对风力发电的深入研究，风力发电机的单机功率在增加，整个风电产业蒸蒸日上。近年来，直驱式永磁同步风力发电机逐步成为研究热点，这种发电机相比其它类型电机有许多优势，比如：电机尺寸小、功率密度高、结构简单等优点，因此其被大量地应用于风力发电领域。永磁同步发电机的控制过程中经常要用到编码器等器件，这就限制了永磁同步发电机的应用场景，也提高了其制造成本。如果采用无速度传感器控制就没有上述缺点，因此无速度传感器控制成了近年来的研究热点[1-2]。

常见的永磁同步发电机无速度传感器控制方法大致分为两类：低速时常采用高频注入法，文献[3-5]通过外加高频激励信号，利用电机本身的凸极特性来获取转子位置。然而，高频注入法仅适用于电机低速情况且复杂度较高；中高速常采用模型法，文献[6-7]研究了基于模型参考自适应的永磁同步电机无位置传感器控制，通过构建电机的参考模型和可调模型，并以Popov超稳定性理论为基础设计自适应律，实现了无速度传感器的电机控制。滑模观测器具有结构简单、鲁棒性强等优点，在永磁同步发电机无位置传感器控制中被广泛研究[8-10]。文献[8]研究了基于滑模观测器的无位置传感器控制，利用Sigmoid函数来替代符号函数以减弱观测反电动势中的高频抖振。然而，基于Sigmoid函数的滑模观测器控制系统由于高频信号切换导致系统存在较大抖振。

扰动观测器算法也广泛用于各种控制系统，如机器人和导弹控制等领域[11-12]。通过扰动观测器得到系统的扰动信号，并将观测结果补偿到系统当中来抵消实际扰动产生的影响。文献[13-14]提出了一种改进的扰动观测器模型，通过中间变量的代换可以避免观测器中对于状态变量的微分运算，减少了控制系统中的噪声信号。文献[15]将永磁同步电机的反电动势作为扰动量，借助中间变量代换避免了计算电流微分，减少了控制系统的噪声信号。然而，文献[15]中的转子角度补偿环节与转速有关，当转速不准确时，会产生较大的补偿误差。

本文基于扰动观测器来进行永磁同步发电机的无速度传感器控制，采用无差拍控制器代替传统的PI电流环。无差拍控制相比PI控制具有动态响应快、电流波动小等优点。然而传统的无差拍控制器中需要用到电机的估计转速和磁链，当这两个参数不准确时，就会造成较大的计算误差，从而使得控制系统变得不稳定。针对这一缺点，本文通过扰动观测器得到电机的估计反电动势，并将其带入无差拍控制器中进行计算，从而消除电机估计转速和磁链不准确对控制系统的影响。

由于反电动势观测器相当于一阶低通滤波器，会造成观测反电动势产生相位延迟和幅值衰减。因此直接由锁相环[16]得到的电机转子角度并不准确，需要进行相应的角度补偿。传统的转子角度补偿方法需要用到永磁同步发电机的估计转速。当电机估计转速不准确时，就会导致补偿角度产生较大误差，进而造成永磁同步发电机的控制精度下降。为了解决这一问题，本文提出了一种新的角度补偿方法，通过增加一个和扰动观测器截止频率一样的滤波器，使两次滤波产生的延迟角度相等，来进行延迟角度的补偿。该方法消除了估计转速在角度补偿中的影响。由于两次滤波中反电动势产生的幅值衰减是相等的，根据这一特点对观测到的反电动势进行幅值补偿。最终将角度及幅值补偿后的反电动势带入无差拍控制器中，消除了电机估计转速和磁链对于控制系统的影响。通过实验验证了该方法的有效性。

1 永磁同步电机数学模型

在α-β坐标系下，表贴式永磁同步发电机的电流状态方程为

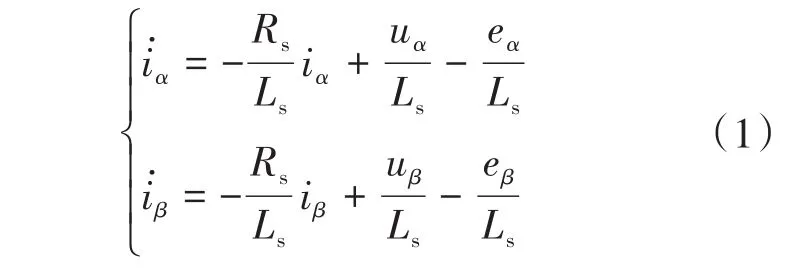
式中：上标“·”为相应变量的状态变量；Rs和Ls为电机定子电阻和电感；iα，iβ分别为电机在α，β轴下的定子电流分量；uα，uβ分别为电机在α，β轴下的定子电压分量；eα，eβ分别为电机在α，β轴下的反电动势分量，可通过下式计算得出：

式中：p为电机极对数；ωr为转子机械角速度；Ψf为电机磁链；θ为电机转子位置角。

2 无差拍电流预测控制

采用前向欧拉法对式（1）进行离散化，并结合式（2）得到离散化的电压方程：

式中：Ts为系统采样时间。

通过Park反变换得到α，β轴参考电流iα_ref（k）和iβ_ref（k）：

式中：下标“ref”为相应变量的参考值；上标“^”为相应变量的估计值。

本文通过扰动观测器得到电机的观测反电动势，然后通过锁相环并进行角度补偿后得到估计转子位置角。

将式（3）中k+1控制周期的α，β轴电流用参考电流代替，可以得到传统的无差拍电流预测控制方程为

式中：上标“*”为相应变量的预测值变量。

从式（5）可以看出，传统的无差拍控制精度与电机转速和磁链相关，当转速或磁链产生较大误差时，整个系统的控制精度将会降低。为了解决这一问题，本文通过扰动观测器观测出电机反电动势，然后对观测到的反电动势进行幅值和角度补偿，最后带入无差拍控制器中，进而消除转速和磁链不准确时对控制系统的影响。

3 基于扰动观测器的转子角庞和速庞估计

3.1 扰动观测器的设计

在静止α-β坐标系下，可将表贴式永磁同步电机的电流方程表示如下：

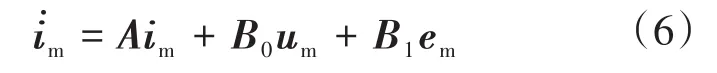
其中

式中：A，B0，B1分别为系数矩阵；I为单位阵；im为定子电流；um为定子电压；em为反电动势，在这里也作为扰动量进行观测。

反电动势估计误差可以表示为

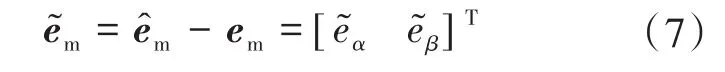
式中：上标“～”为相应变量的估计误差。

初等扰动观测器的表达式为[17]

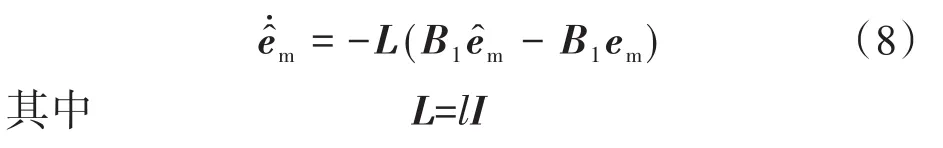
式中：l为扰动观测器增益。

文献[17]中介绍了观测器增益l对于转子位置估计误差和估计转速的影响，为了获得较好的控制效果，本文选取l=-5。

将式（6）代入式（8）中得：

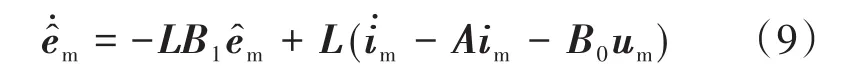
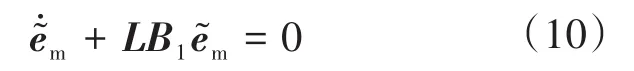
由于式（9）中存在定子电流的微分，求导过程会产生噪声，将会影响观测器的估计效果。为了解决这个问题，通过采用中间变量代换的方法设计了一种新的扰动观测器：

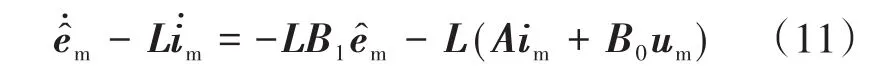
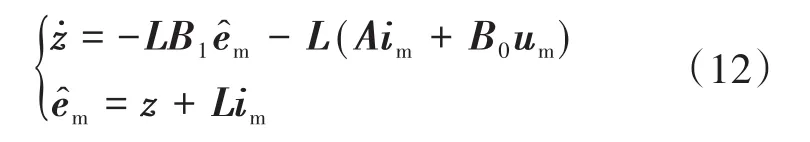
通过式（12）可以看出，通过中间变量z的代换，在计算反电动势估计值的过程中就可以消除电流的微分运算，从而避免引入噪声。

3.2 李雅普诺夫稳定性分析

李雅普诺夫方程为

对式（13）进行求导，并结合式（9）可得：

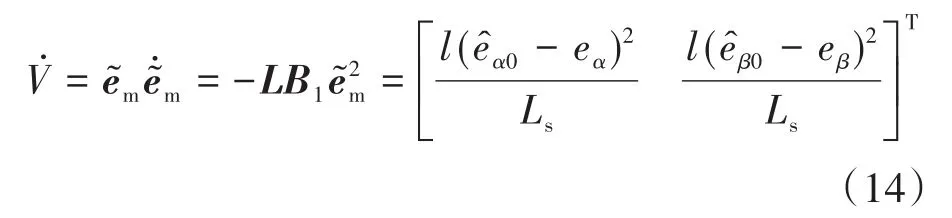
对于式（14），当l<0时，V̇<0，满足李雅普诺夫方程稳定性条件。

3.3 改进的观测角度补偿

根据式（8）可以计算得出反电动势观测器的传递函数：

由式（15）可以看出，反电动势观测器相当于一阶低通滤波器。通过观测器得到的估计反电动势会产生相位延迟和幅值衰减，锁相环通过估计反电动势得到的转子角度和实际转子角度相比就会有角度误差。因此，必须对其进行补偿。

传统的角度补偿[15]常采用下面方法进行补偿：

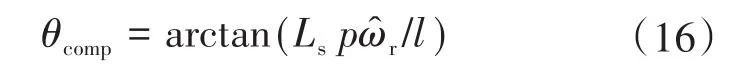
式中：θcomp为电机补偿角。

由式（16）可以看出传统的角度补偿方法对于电机转速依赖性过高。控制系统切换到无速度传感器模式后，在电机转速估计不准确时，就会产生较大的角度补偿误差，进而影响控制系统的稳定性。针对这一缺点，提出了一种改进的转子角度补偿方法，以消除转速对角度补偿的影响。

图1为本文所提改进的转子角度补偿框图。

图1 改进的角度补偿框图Fig.1 The frame diagram of the improved angle compensation

由式（15）可知，eα和eβ经过扰动观测器可以看作是经过了一阶低通滤波器，通过锁相环得到的转子角度θ1和实际转子角度相比有一定的角度延迟，需要对θ1进行角度补偿。因此，可构建另一参数与其完全相同的低通滤波器，即ωc=-l∕Ls，使反电动势经过观测器和低通滤波器产生的角度误差Δθ相同。最终经过角度补偿后的转子位置角θ̂=θ1+Δθ。该角度补偿方法与永磁同步电机转速无关，因此当观测器的估计转速不准时，并不会影响到转子位置角的补偿。

3.4 观测反电动势的幅值补偿

由于反电动势观测器相当于一阶低通滤波器，因此得到的反电动势观测值会产生幅值的衰减。为了得到准确的电机反电动势信息，需要对其进行相应的幅值补偿。由于两次滤波器对于反电动势幅值衰减的效果相同，根据这一特点设计观测反电动势的幅值补偿。

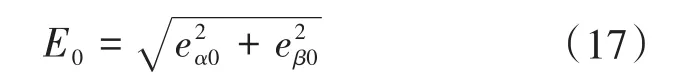
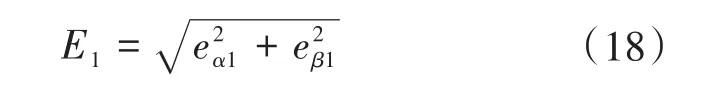
根据式（17）、式（18）可知，低通滤波器所产生的幅值衰减为

通过结合图1的角度补偿可以得到最终的电机反电动势为

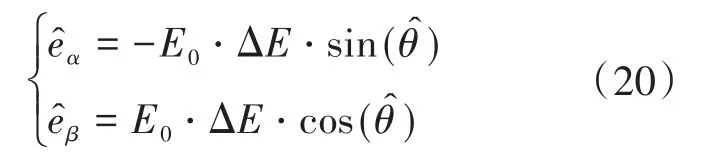
通过式（20）即可得到准确的电机估计反电动势，然后将经过幅值和角度补偿的估计反电动势代入无差拍控制器中，来消除电机转速和磁链对于控制系统的影响。

4 实验研究

为了验证本文改进的转子角度补偿控制效果，在图2所示的实验平台上进行实验分析。

图2 实验平台Fig.2 Experimental platform

永磁同步发电机参数设置如下：极对数p=4，电感Ls=29 mH，定子电阻Rs=1.15 Ω，直流母线电压VDC=600 V，转动惯量J=0.008 6 kg·m2，永磁磁链 0.458 Wb，额定电流I=10 A，额定转矩T=35 N·m，额定转速n=1 000 r∕min。

实验平台包括实时仿真系统HIL和快速原型控制器RCP，其中电力电子系统是利用StarSim FPGA Solver按100 μs的步长实时仿真；控制算法模型运行在RCP控制器上，实时仿真器和快速原型控制器通过真实的物理IO口互连。图3为永磁同步发电机控制系统的结构框图。

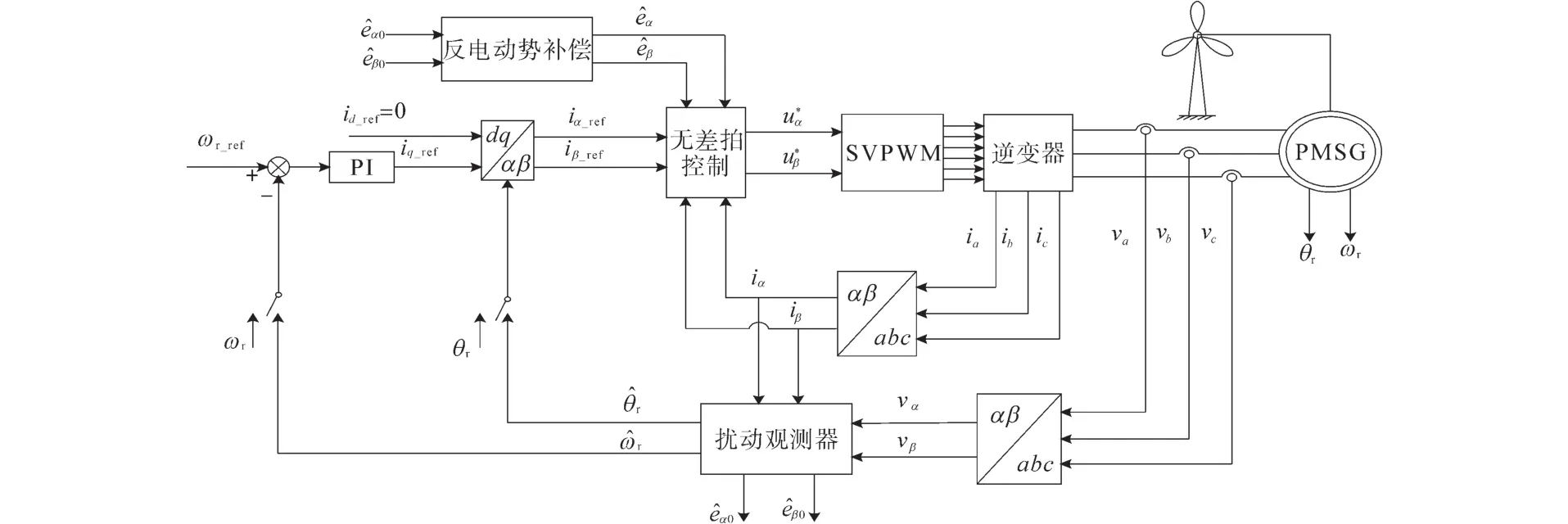
图3 基于扰动观测器的无速度传感器控制系统框图Fig.3 Block diagram of speed sensorless control system based on disturbance observer

图4为电机在满载运行时转速突变后的α相反电动势波形。

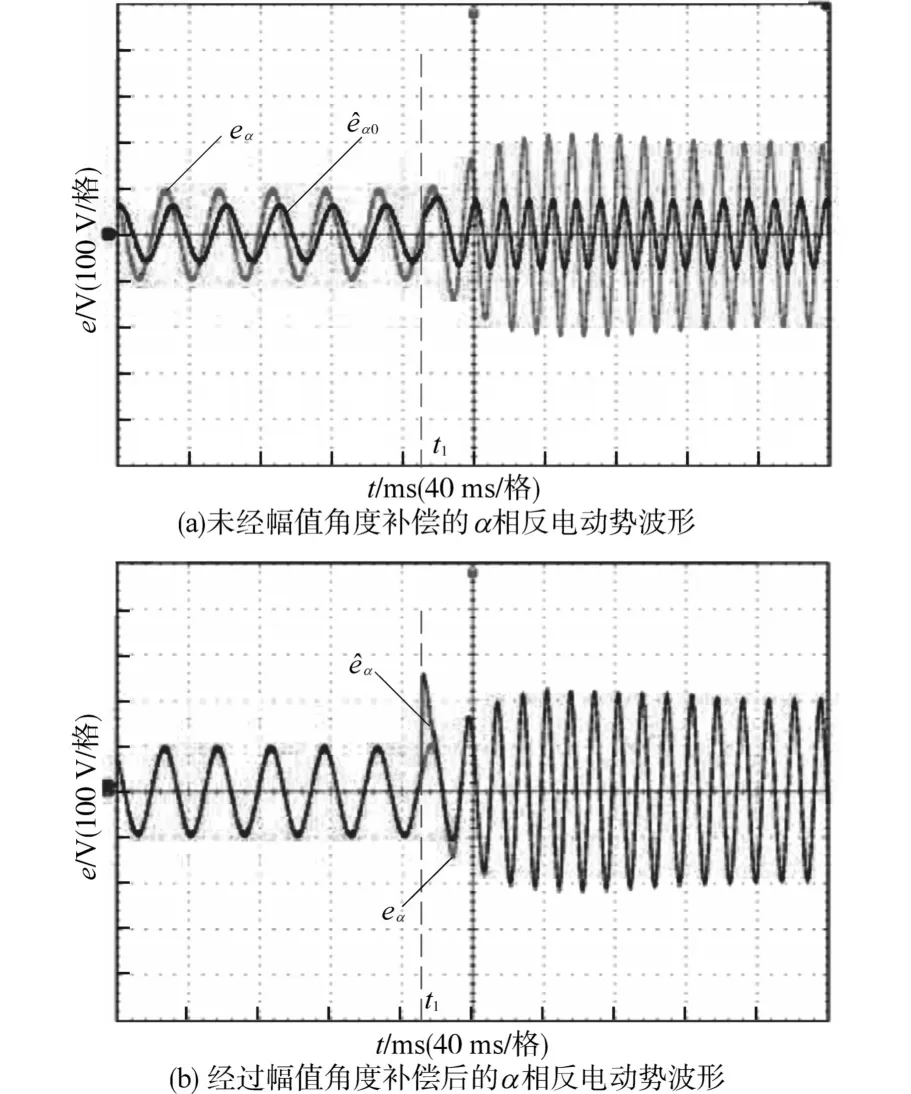
图4 转速突变后α相反电动势波形Fig.4 The waveforms of α phase EMF after sudden change of rotational speed

图4a为幅值角度补偿前观测器观测出的α相反电动势êα0和实际反电动势eα的波形对比图，可以看出，观测器观测出的电机反电动势相比实际反电动势存在明显的相位延迟和幅值衰减。图4b为经过幅值角度补偿后的α相反电动势波形，可以看出经过补偿后的反电动势êα和电机实际反电动势eα完全重合。当电机转速在t1时刻从500 r∕min 加速到 1 000 r∕min时，补偿后的估计反电动势可以准确地跟随实际反电动势，证明了本文的估计反电动势幅值角度补偿方法具有良好的动态响应性能。

图5为电机进行加减速时电机转速和转子角度波形图。

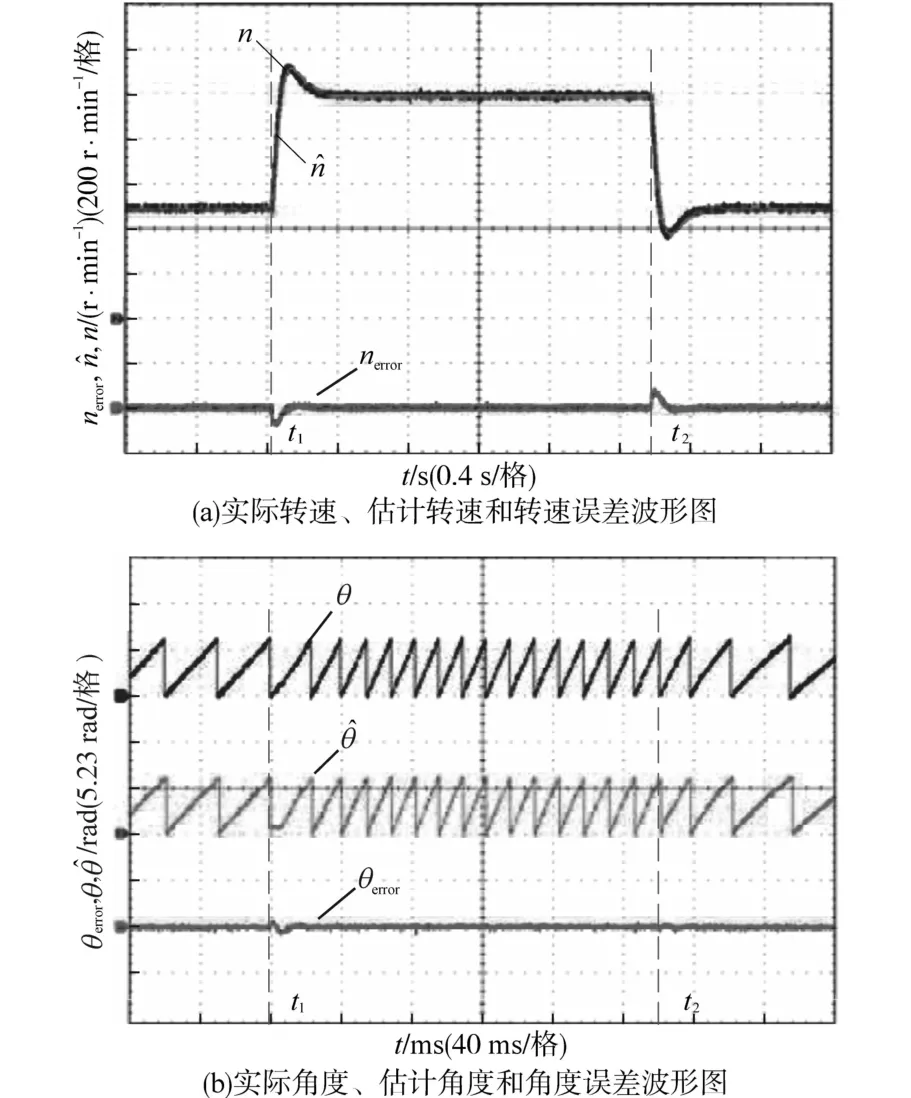
图5 电机加、减速动态响库波形Fig.5 Dynamic response waveforms of motor acceleration and deceleration

从图5a可以看出当电机转速在t1时刻从500 r∕min加速至1 000 r∕min时，转速误差突然增大约80 r∕min，估计转速n̂在PI控制器的调节下能够快速、准确地跟随上实际转速n；从图5b可以看出当电机转速突变后，转子位置角度经过短暂的波动后迅速稳定，稳定后角度误差接近于零。由此可见，扰动观测器在转速变化过程中可以提供良好的动态响应性能，所提出的转子角度补偿方法也具有良好的稳定性。

图6为常规角度补偿方法的实验波形图，电机实际转速为500 r∕min。为了模拟实际控制中估计转速不准的情况，在t1时刻估计转速跳变为600 r∕min。由图6可以看出，电机估计转速不准确时，转子角度出现较大的误差，与图5b中采用改进的角度补偿方法的控制效果存在明显的差别。改进的角度补偿方法中没有使用电机的估计转速，从而消除了电机估计转速对补偿精度的影响。

图6 常规角度补偿实验波形图Fig.6 Experimental waveforms of conventional angle compensation

为了验证该方法的有效性，使电机运行在无速度传感器模式，转速为1 000 r∕min。图7为对电机突加、突减50%负载时的动态响应波形。

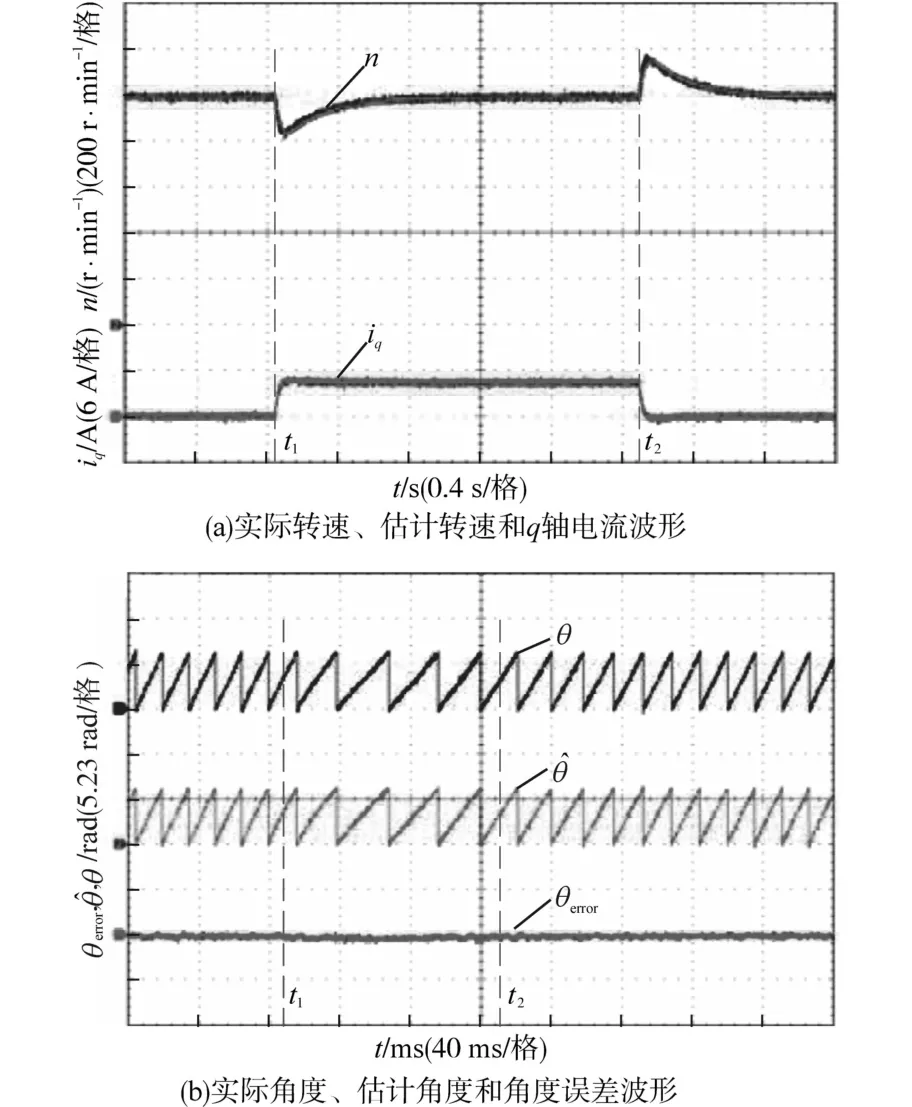
图7 电机加、减负载动态响库波形Fig.7 Dynamic response waveforms of motor loading and reducing load

可以看出，当电机在t1时刻突加负载时，q轴电流明显增大，电机转速突然下降约160 r∕min，随后在PI控制器的作用下迅速上升至给定转速。当电机在t2时刻突减负载时，q轴电流迅速减小，电机转速突然上升约160 r∕min，然后迅速下降至给定转速。在上述动态过程中可以看出，估计转速始终和实际转速一致，转子角度误差变化较小，对电机的稳定运行没有影响。

5 电机厑数不匹配的实验波形

无差拍电流预测控制是一种依赖于永磁同步电动机模型参数的控制方法。扰动观测器观测反电动势同样需要用到电机参数。然而，当电机运行一段时间后，会有温度上升和磁饱和现象，实际电机参数将会改变，进而导致电机参数和控制器参数不匹配，影响系统的控制效果。为了测试在电机Rs和Ls参数不匹配的情况下该方法控制效果，进行了以下实验进行验证。

图8为观测器和无差拍控制中电阻Rs0改变为电机实际电阻Rs的1.5倍时，电机在给定转速500 r∕min半负载运行时的加减速波形图。由图8a可以看出，当电机转速在t1时刻从500 r∕min加速至1 000 r∕min时，可以看出估计转速能够准确地跟随实际转速。电机转速仅在突变时产生较大的转速误差，随后误差在转速环PI控制器的作用下迅速减小。由图8b可以看出，估计出的转子角度可以准确地跟随实际电机转子角度。转子角度误差在转速上升时有所偏移，随后误差迅速下降，对电机稳定运行无明显影响。当电机转速在t2时刻从1 000 r∕min降低至500 r∕min 时，电机估计转速和实际转速同样可以准确地跟随实际值。

图8 电机定子电阻失配Rs0=1.5Rs时加、减速波形图Fig.8 Acceleration and deceleration waveforms of motor stator resistance mismatch when Rs0=1.5Rs

图9为观测器和无差拍控制中电感Ls0改变为电机实际电感Ls的1.5倍时，电机在给定转速为500 r∕min半负载运行时的加减速波形图。电机分别在t1和t2时刻进行加减速。由图9可以看出，当电机进行加减速时，转速和角度产生一定的误差，随后在控制系统的调节下迅速收敛至零附近。由图8和图9可以看出，在系统参数不准确的情况下，本文的方法仍然具有良好的控制效果。

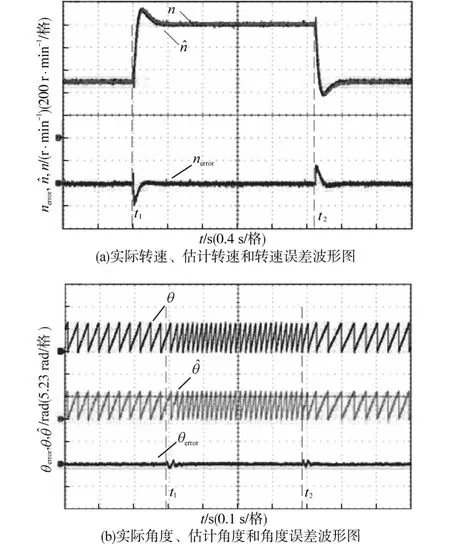
图9 电机定子电感失配Ls0=1.5Ls时加、减速波形图Fig.9 Acceleration and deceleration waveforms of motor stator inductance mismatch when Ls0=1.5Ls

6 结论

基于扰动观测器和改进的无差拍电流预测控制，本文设计了一种用于永磁同步风力发电机的无速度传感器转子角度补偿方法。

针对常规的转子角度补偿精度受估计转速影响这一缺点，提出了一种新的转子角度补偿方法。通过构建一个截止频率和观测器相同的低通滤波器，实现估计转子角度的准确补偿。

针对无差拍控制精度受到估计转速和磁链的影响这一缺点，采用扰动观测器得到估计反电动势，并对估计反电动势进行幅值和角度补偿，将补偿后的估计反电动势代入无差拍控制中进行计算，消除了无差拍控制中电机估计转速和磁链对控制系统的影响。

最后通过实验结果可以看出，改进的无差拍控制和转子角度补偿方法具有良好的控制效果，验证了该方法的有效性。