磨合过程中液体润滑实现超低摩擦的混合模型研究

方燕飞,马丽然

(1.华侨大学 机电及自动化学院,福建 厦门 361021;2.清华大学 摩擦学国家重点实验室,北京 100084)

液体超滑作为新兴润滑技术备受人们关注，为精密机械降低能量消耗提供一种有效的润滑技术手段.减小相对运动表面间的摩擦磨损，实现超低摩擦是机械工程中追求的目标之一，研究学者们分别在固体润滑和液体润滑体系中实现了超低摩擦的润滑状态[1-2].由于液体润滑的稳定性较好，液体超滑体系备受研究学者的关注.在过去的30年中，人们对于液体超滑的认识也越来越深入，针对不同液体超滑体系，提出不同的物理机制[3-4].

液体超滑在试验上通过球-盘润滑滑动下实现，在磨合一定时间后，流体动压效应形成稳定的润滑薄膜，对超低摩擦实现有重要作用.Kato等[5-6]较早系统地研究了陶瓷在水润滑下的摩擦行为，发现经过一段磨合阶段，润滑体系可以达到0.002～0.007的超低摩擦系数(μ)，由于摩擦化学反应，在陶瓷界面处形成双电层效应，在流体动压下形成超低摩擦的液体薄膜.Li等[7]采用磷酸溶液在氮化硅对二氧化硅陶瓷摩擦副进行摩擦试验，发现经过磨合后，液体润滑体系进入超低摩擦状态，摩擦系数为0.004，他们认为主要与磨合过程中接触界面形成Stern层、润滑介质中水分子挥发以及润滑介质的氢键网络有关[8]，随后他们发现在硫酸和甘油混合溶液润滑下，摩擦副也产生了超低摩擦系数[9].Han等[10-11]采用盐离子溶液在宏观尺度下实现液体超滑，发现在磨合前期，陶瓷表面发生摩擦化学反应，表面生成二氧化硅层和离子形成的水合作用承担部分载荷在流体压协同作用下实现超低摩擦.李金鹏等[12]在研究聚合物刷水润滑性能也发现通过水合效应和流体动压效应协同作用能够增强液体润滑性能.Ge等[13]采用离子液体作为润滑剂与纯水混合在氮化硅摩擦副上实现超滑，认为复合摩擦化学层、水合层和流体膜促进了超润滑性.Jia等[14]合成了聚乙二醇甲醚丙烯酸酯并将其配制成水溶液在陶瓷球-盘上开展了其摩擦润滑行为的研究，实现超低摩擦系数(<0.01).润滑机理是由于接触表面形成的吸附膜和流体动压效应协同作用促进超低摩擦.通过这些文献的研究表明，可以发现在液体超滑中流体动压作用起着重要的作用，结合相应的表界面效应进一步降低摩擦，比如水合吸附膜和双电层效应等[15]，特定的摩擦副可降低表面粗糙峰边界摩擦系数.Fang等[16]结合双电层效应和流体动压协同作用，建立了在稳定阶段下宏观水基液体超滑数值模型，模拟计算水基液体超滑的实现条件，为液体超滑的理论设计提供了一定的理论指导.

液体超滑实现中还存在1个重要阶段-磨合现象.在磨合过程中，接触界面处发生摩擦化学反应，磨损表面变得光滑，表面粗糙度有效降低，其次液体润滑介质在界面处有效黏度增大，在润滑区形成流体动压薄膜支撑法向载荷，最后液体润滑状态发生转变，由最初的边界润滑或混合润滑逐渐过渡到流体薄膜润滑.相关的试验研究发现了磨合现象对液体超滑实现的规律.Deng等[17-18]发现了在磨合过程中球-盘滑动中流体动压效应逐渐增强，形成液体薄膜而实现液体超滑.Guo等[19]探讨了磨合过程中液体润滑超低摩擦的影响规律.因此针对磨合过程液体润滑性能演变，建立相应的数值建模显得十分有必要，可提供自上而下的液体超滑设计方法.在液体润滑滑动过程磨合数值研究中，有些学者对磨合过程润滑性能建模上提出了相应的数值模型.Zhu等[20]基于Archard理论与确定性混合润滑模型相结合来预测摩擦过程中磨损体积和润滑状态分析.随后在近几年中也有学者针对混合润滑磨合磨损建模提出了相应的数值模型.Azam等[21]建立了1个确定性模型来模拟摩擦反应膜的生长和磨损.Furustig等[22]建立了双尺度磨损模型研究液压马达在混合润滑下表面形貌的演变，并开展试验验证.Akchurin等[23]建立混合润滑滑动接触磨损颗粒形成模型，在模型中引入磨损颗粒生成准则从而确定颗粒磨损量.Zhang等[24]采用统计学方法预测了线接触混合润滑下磨合表面和摩擦系数演变规律.Pei等[25]提出了基于能量的Arrhenius方程与混合弹流润滑(EHL)模型相结合，预测混合润滑中的点接触磨损过程模型.然而，这些模型中，未完全引入相关物理参数随时间变化规律，从而建立点接触磨合过程中液体润滑演变及实现超低摩擦的综合模型，为液体超滑设计提高效率.

综上所述，针对点接触磨合过程液体润滑状态演变，基于流体润滑方程、粗糙峰接触力学、磨损方程以及提出磨合过程中液体黏度、表面粗糙度和磨损率的时变函数，建立磨合过程中液体润滑性能演变的混合模型并开展数值分析，主要考察磨合过程中液体黏度和表面形貌特征演变对液体润滑性能及其超低摩擦系数的影响规律.因此，所建立的混合数值模型可为液体超低摩擦润滑体系设计提供数值参考依据.

1 磨合过程中液体润滑演变数学模型

1.1 润滑控制方程

在磨合过程中，表面粗糙度直接影响液体润滑状态，需要建立考虑表面粗糙度对润滑性能的影响.采用Patri和Cheng提出的考虑表面粗糙度影响的平均流量润滑模型[26]，即在 Reynolds方程中引入流量因子来修正公式，表达为

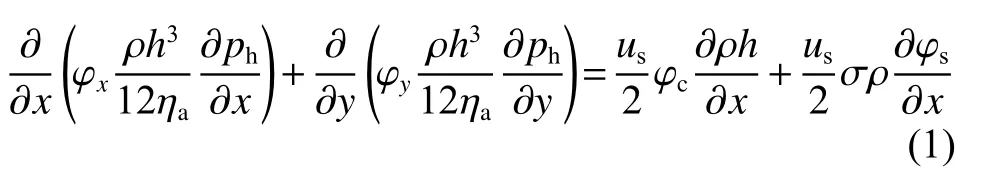
式中：h为名义膜厚，ph为平均流体压力，ηa为液体黏度，ρ为液体密度，σ为表面综合粗糙度，us为滑动速度，φx和φy为在x和y方向上的压力流量因子，φs为剪切流量因子，φc为接触因子，对于压力流量因子、剪切流量因子和接触因子的确定，在实际计算中，可以采用经验公式确定，具体的参数表达读者可以参考文献[27-28]确定.该方程的边界条件为

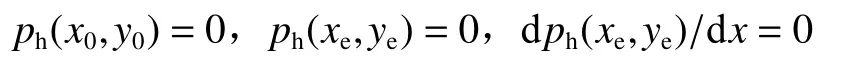
其次润滑介质黏压方程采用Roelands黏压方程表达为

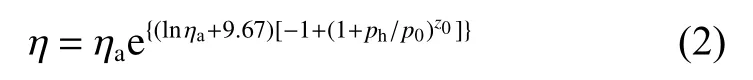
式中，ηa为液体润滑介质的等效黏度；z0为Roelands压力黏度指数，p0为压力黏度系数.

润滑介质的密度压力关系采用Dowson-Higginson形式：

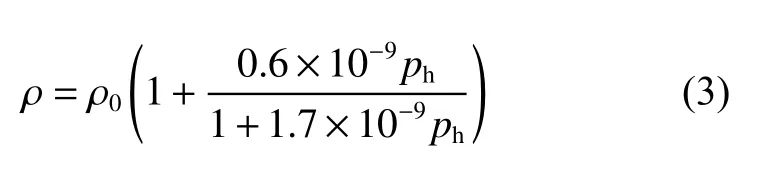
式中，ρ0为常压下润滑剂密度.

在球-盘润滑表面形成的润滑膜厚为

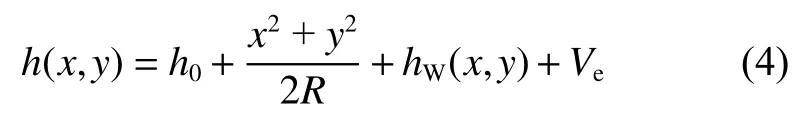
式中，h0为两个润滑表面之间的刚性相对位移；R为接触表面曲率半径；hw(x,y)为在磨合过程中表面轮廓的变化高度；Ve为两个表面接触变形，可采用Boussinesq积分形式求解：

式中，E＇为综合弹性模量，pasp为粗糙峰接触压力.

1.2 粗糙峰接触模型

润滑接触区中存在粗糙峰间的接触，表面粗糙峰接触会发生塑性变形、弹塑性变形和弹性变形，从而导致接触表面轮廓的磨损.在本研究中，对于表面粗糙峰接触力学行为采用K-E粗糙峰接触模型[29-31]来计算粗糙峰接触压力，表达为

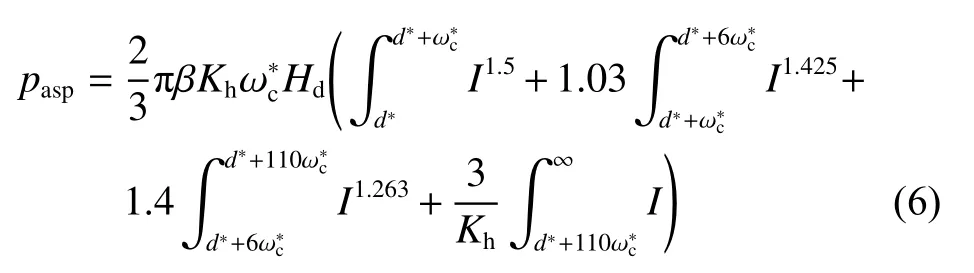
式中β为粗糙表面参数，定义为β=NRasσ，通常设置0.05；N为粗糙峰数；Ras为表面粗糙峰半径；Kh为接触副中较软材料泊松比v有关的表达式，定义为Kh=0.454+0.41v；无量纲的临界变形量，定义为=Hd为材料的硬度值；Iα为被积分式子α为1.5、1.425、1.263或者1；φ*(z*)为无量纲的粗糙峰高度概率密度函数，定义为z*是无量纲粗糙峰高度z*=z/σ，z是从粗糙面平均高度到粗糙峰的高度，σs为粗糙峰高度的标准差；h*为无量纲名义油膜厚度；d*是无量纲粗糙峰平均高度与光滑表面的距离；为h*与d*之差，由决定[30].

1.3 磨合过程控制方程

在球-盘滑动磨合过程中，采用经典的磨损模型—Archard 模型[32]确定接触轮廓的磨损变化.Archard磨损模型表明表面磨损深度与材料属性和接触方式呈一定的线性关系，由于该公式简洁，在数值中广泛应用.Archard 模型公式表达为

式中,kw为磨损系数；s为磨合滑动的距离；p为接触区压力分布.通过公式(7)可以看出：在磨损过程中，表面磨痕深度与表面接触压力呈正相关.因此，在计算每一微小时间段Δt内，认为表面接触压力保持不变，表面接触副滚动一微小段距离Δs后，经过一段时候后，接触表面轮廓磨合磨损深度为

在液体超滑磨合过程中，由于环境因素和摩擦副材料，添加润滑剂容量一定时，比如水基溶液中水分子在磨合过程发生蒸发，导致液体溶液浓度上升，液体黏度增大；同时如陶瓷在水溶液中，在摩擦接触作用下，润滑介质与摩擦副表面发生摩擦化学反应，在接触区内的润滑黏度特性、表面粗糙度和磨损率将随着磨合时间发生着相应的变化，从而导致润滑状态演变.液体润滑体系在磨合过程中实现超低摩擦状态的试验结果[18]表明：整个过程中可以划分为两个阶段：边界/混合润滑向着流体动压薄膜润滑转变过程以及超低摩擦润滑的稳定阶段.然而由于在摩擦磨损试验中，这些变化因素随着环境、工况条件而引起的差异，借鉴相关的文献[33-36]所提出对液体润滑状态下在磨损过程中润滑接触副的磨损演变规律，这里我们提出采用“S”型状态时变函数来描述磨合过程中液体黏度、接触副表面粗糙度和磨损系数的变化.在磨合磨损过程中，由于溶液的蒸发和摩擦诱导化学反应，液体等效黏度ηa随着时间的变化为

式中，η∞为稳定阶段液体的黏度，η0为初始阶段大气压力下液体的黏度；Bv和Cv为液体黏度变化的时间参数.

而对于润滑接触副粗糙表面，在磨合过程中由于液体润在润滑区起到摩擦化学抛光作用，表面粗糙度和磨损率从磨合初期较大值逐渐降低到1个较小稳定数值，在磨合过程中粗糙度σ和磨损率kw随时间的演变规律也采用“S”型状态时变函数来描述，分别如以下公式所示：

式中，σ∞为稳定阶段粗糙度，σ0为起始阶段粗糙度，Br和Cr为表面粗糙度变化时间参数；k∞为稳定阶段磨损率，k0为起始阶段磨损率，Bw和Cw为磨损率变化时间参数.

那么对于公式(9)、(10)和(11)而言，我们针对球-盘磨合过程液体润滑状态演变对液体润滑黏度特性、表面粗糙度和磨损率提出时变函数.球-盘磨合过程润滑状态从磨合初期阶段混合润滑逐渐过渡到磨合稳定阶段的流体薄膜润滑状态，从而获得超低摩擦系数状态.公式(9)、(10)和(11)中的参数设置可以选择在磨合过程从初始时刻t=0到总的磨合时间t=T，当磨合时间t=0时，黏度、表面粗糙度和磨损率分别等于初始值η0、σ0和k0；当达到稳定阶段时候，黏度、表面粗糙度和磨损率分别等于η∞、σ∞和k∞.其他的变化参数根据试验中磨合过程液体超滑曲线规律而确定出来.

1.4 载荷平衡与摩擦系数估算

在球-盘滑动试验中，球受到法向施加载荷Fn为恒定.在润滑接触区中由粗糙峰接触压力和流体动压来共同承担法向载荷.根据载荷平衡，可得到：

在磨合过程中摩擦系数演变是值得关注的参数.在本模型中，润滑接触区的摩擦力Ff主要由表面粗糙峰边界润滑剪切力Fc和流体剪切力Fh组成进行估算，其公式如下：

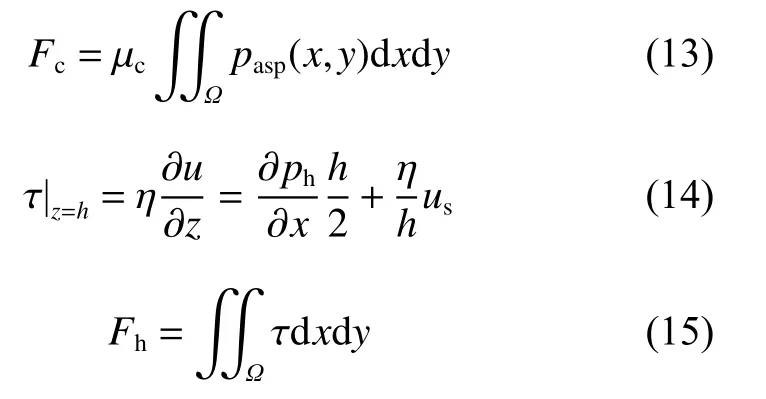
式中：µc为粗糙面接触摩擦系数，τ为表面间流体剪切应力.

因此，在液体润滑接触区内摩擦系数µ表示为

2 数值求解

磨合过程液体润滑演变的混合模型数值求解过程中，计算程序包括混合润滑方程求解、粗糙峰接触力学、Archard表面轮廓磨损和相关物理参数变化进行多参数耦合计算.在混合润滑计算中，对润滑方程进行无量纲化，采用Hertz接触半径a和最大接触压力PH，求解采用有限差分法进行离散化.设定求解域为Ω∈(-3.0a≤x≤3.0a;-3.0a≤y≤3.0a)，采用Gauss-Seidel迭代法和Jacobbi迭代法求解润滑方程[37]得到润滑平均膜厚和流体压力.根据平均膜厚结合粗糙峰接触压力公式，得到润滑区内的粗糙峰接触压力分布，采用低松弛迭代得到新的粗糙峰接触压力分布[38].当同时满足载荷平衡和压力分布收敛条件，前后两次迭代的相对误差均小于0.000 1，获得润滑区的平均膜厚、流体压力和粗糙峰接触压力分布.为了提高计算效率，本程序计算中采用快速傅里叶变换求解接触区弹性变形[39].

当润滑区流体压力和表面粗糙峰接触压力确定后，利用Archard模型计算球表面磨损深度.总磨合时间Tr划分为N个时间步，每个时间段为Δt=Tr/N.那么在第m+1次中，更新磨合磨损的轮廓

计算接触区内磨损深度，得到磨损后的接触轮廓.再根据公式(16)，就可以计算此时润滑接触副的摩擦系数.判断是否达到总磨合时间，若未达到，则更新润滑黏度、粗糙度和磨损率，进入下一次液体润滑性能计算.当达到了总磨合时间(迭代次数)，则计算程序结束.本数值计算流程如图1所示.

Fig.1 Computational flow chart of the hybrid model of liquid lubrication evolution during running-in图1 磨合过程液体润滑演化混合模型计算流程图

3 结果与讨论

研究在磨合磨损过程中，液体润滑摩擦系数的演变，采用表1所列的参数作为输入值进行仿真研究.根据Hertz接触理论可以得到，接触的半径为a=39.03 μm，接触最大压力为PH=949 MPa.在数值仿真中，粗糙表面的边界润滑摩擦系数为0.15，在磨合过程中，总磨合时间为Tr=1200s，其中等效黏度变化、表面粗糙度和磨损率的变化参数采用黏度变化参数Bv=120s，Cv=600s；表面粗糙度变化参数Br=90s，Cr=450s；磨损率变化时间参数Bw=90s和Cw=450s，这些参数可以根据试验情况而定.

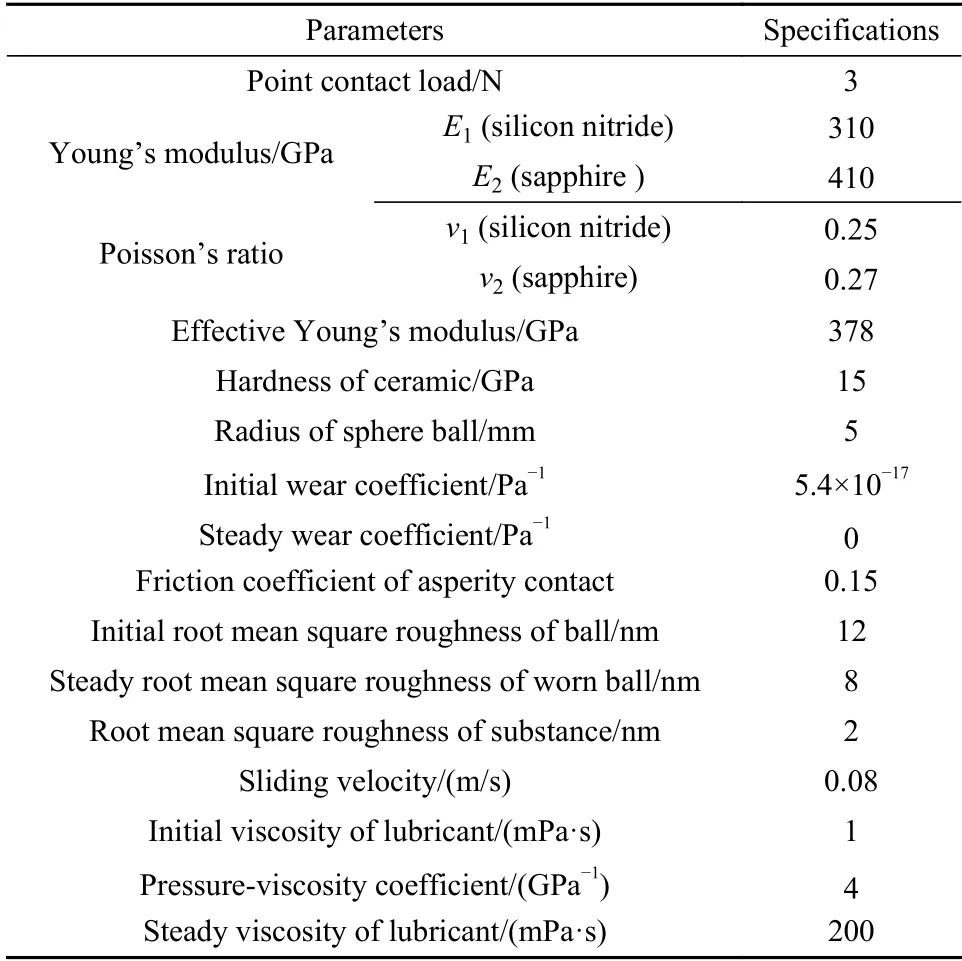
表1 输入仿真计算参数Table 1 Input simulation parameters

图2所示为磨损过程中，液体等效黏度变化曲线，假设在磨合开始初期，液体黏度数值很小，随着时间的推移，黏度逐渐增加，在稳定阶段最终达到较大黏度值.产生这种现象主要是由两方面引起：第一、在试验过程中润滑剂的选择，特别是在水润滑介质磨合过程中水分子蒸发，液体溶剂浓度变得稠密，例如磷酸和甘油等这类常用的液体润滑剂；第二、由于陶瓷材料在磨合过程中产生二氧化硅胶体，这两种因素会导致润滑介质的等效黏度急剧上升.图3显示了在所示为磨合磨损过程中表面粗糙度和磨损率的变化.磨合前期表面粗糙度值较大，随着时间的推移，在初始阶段中表面粗糙度逐渐降低，润滑区界面黏度增加，流体润滑膜有效形成，润滑状态逐渐从混合润滑过渡到流体薄膜润滑，有效形成流体膜润滑，两个运动表面逐渐被隔开，磨损率逐渐减少.当润滑体系在流体薄膜润滑形成后，接触副材料磨损率为0.

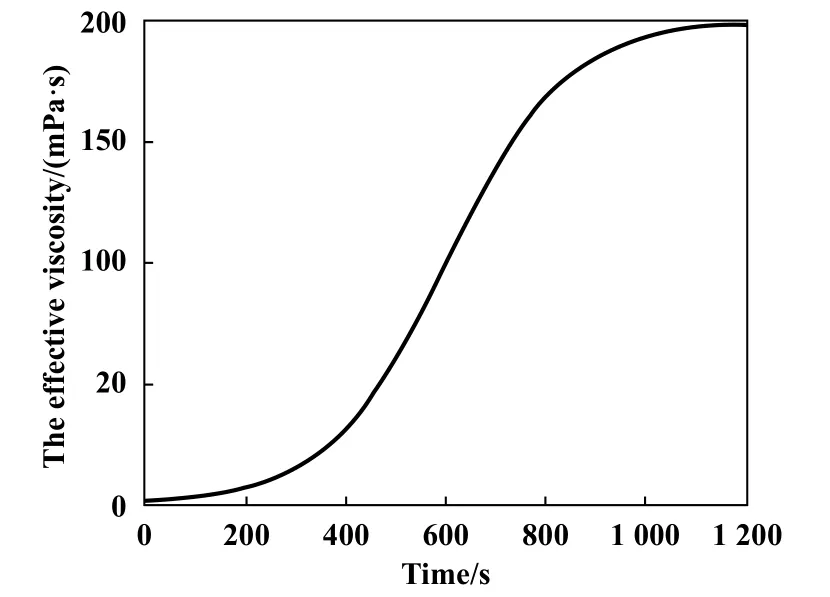
Fig.2 The evolution of liquid effective viscosity with time during running-in process图2 液体等效黏度在磨合过程中的变化曲线

Fig.3 The evolution of the roughness and wear rate with time during running-in process图3 接触副表面综合粗糙度和磨损系数在磨合过程中变化趋势

3.1 磨合过程轮廓和润滑性能演变

图4所示为在不同磨合时刻的球轮廓变化.由图4(a)可知在磨合初始阶段，表面轮廓磨合深度比较剧烈，到了磨合后期，球表面轮廓变化基本上比较缓慢.图4(b)所示为磨合后球面最终轮廓三维图，球表面轮廓变得十分平整.图5所示磨合过程中不同时刻，接触区内的粗糙峰接触压力、油膜流体动压压力分布和润滑总压力在y=0轴向分布.从图5中可以明显看出，在磨损开始接触区的压力绝大部分由粗糙峰接触压力承当，随着磨损过程中的润滑介质的黏度上升和磨损表面的粗糙度降低，在磨损过程中，载荷逐渐润滑薄膜承担，在稳定阶段上，粗糙峰接触压力几乎没有，润滑区的流体压力分布和润滑区的总压力分布基本一致，承担着球上所施加载荷.

Fig.4 The ball profile change during the running-in process along the y=0 axis (a);and the final worn surface three-dimensional profile(b)图4 (a)为在y=0轴上不同磨合时刻的球轮廓变化情况及(b)磨合后的表面轮廓三维图

Fig.5 (a)Fhe evolution of pressure distribution in the running-in process asperity contact pressure along the y=0 axis; (b)Film hydrodynamic pressure along the y=0 axis; (c)Total contact pressure along the y=0 axis; (d)Film hydrodynamic at final state图5 (a)磨合过程不同时刻下润滑接触区粗糙峰接触压力沿着y=0轴向分布；(b)流体动压压力沿着y=0轴向分布；(c)润滑区接触总压力沿着y=0轴向分布和(d)最终时刻整个润滑区内流体压力分布情况

3.2 液体润滑的摩擦系数演变

图6所示为整个磨损过程中，粗糙峰承载和流体动压承载比变化.在磨合初期，表面粗糙峰承担绝大部分载荷，液体流体动压效应极其微弱，在磨合前期磨损率较大，磨合面积增大，从而导致粗糙峰承载比有所上升.随着磨合时间的推移，界面等效黏度有效上升和接触表面粗糙峰降低，液体流体动压效应逐渐增强，摩擦副进入到润滑状态转变过程.最终在稳定阶段，流体润滑薄膜承担了绝大部分的载荷，粗糙峰承载比承担了极少部分.

图7所示为在磨合磨损过程中的摩擦系数演变.从中明显看出，磨损过程初期，接触副摩擦系数较大基本上大于0.1，磨合前期在100 s阶段中，由于液体的黏度基本保持不变，摩擦副处于混合润滑接触，磨合中接触面积逐渐增大，从而使得粗糙峰接触增大，导致粗糙峰的剪切作用增大，摩擦系数上升.随后，液体的黏度增大，在混合润滑中，流体动压效应增大，粗糙峰接触承载随之降低，从而导致摩擦系数下降.在稳定阶段，摩擦系数出现小于0.01，处于液体超滑状态，在该阶段摩擦系数主要由液体黏性剪切决定.在数值进一步模拟过程中，边界摩擦系数设定在0.05～0.30之间变化，可以看出在磨损初期，摩擦系数由边界润滑状态的摩擦决定，随着磨合时间推移，摩擦系数逐渐下降；最终在稳定阶段，摩擦系数主要由流体膜的剪切强度而决定，摩擦系数保持稳定.由于在稳定状态中，还可能存在少量的粗糙峰接触，如图6所示，边界摩擦系数较大值时，使得液体润滑无法进入到液体超滑.因此，调控粗糙峰边界润滑的摩擦系数和流体膜的剪切强度是液体润滑实现超低摩擦的关键因素.

Fig.6 Evolution of asperity contact ration and film load ratio during running-in process图6 磨合过程中润滑区内粗糙峰承载比和流体膜承载比的变化

Fig.7 The effect of boundary friction coefficients on the evolution of friction coefficient during running-in图7 磨合过程边界摩擦系数对摩擦系数演变的影响

3.3 磨合稳定下黏度和粗糙度对摩擦系数的影响

考察在磨合稳定阶段，界面等效黏度对液体润滑体系的摩擦行为的影响.在磨合稳定阶段，液体黏度的等效黏度η∞从50到200 mPa·s之间变化，其他参数列于表1中.液体润滑在磨合过程中的摩擦行为演变如图8所示.由图可知在磨合初期，摩擦副处于混合润滑状态下，液体润滑的摩擦系数变化基本上较为一致.随着磨合时间推移，液体等效黏度逐渐增大，摩擦系数下降.在磨合稳定阶段，液体等效黏度对摩擦系数有直接影响，液体等效黏度较小时，无法形成较厚的润滑膜，在润滑区内的粗糙峰还存在着部分接触，从而导致摩擦系数无法降低到0.01；当液体等效黏度较大时，润滑区形成全膜润滑，润滑薄膜厚度也随之增大，粗糙峰承载比趋于0，摩擦系数小于0.01.在液体等效黏度为150和200 mPa·s时，摩擦系数基本相差不大，都进入液体超滑状态.此时流体薄膜润滑区摩擦力由流体黏度剪切作用所决定，在这种情况下，可以预见当等效黏度大于200 mPa·s时，润滑区内流体膜剪切作用的摩擦系数反而会有所增大.从数值分析可以知道，在磨合过程中，液体润滑介质的等效黏度较低时，无法形成完全流体薄膜润滑，出现粗糙峰接触，润滑体系的摩擦系数无法进入到液体超滑状态；随着磨合时间推移润滑介质在固-液界面效应作用和水分子蒸发下，润滑剂等效黏度增大，可形成有效地流体薄膜从而实现摩擦系数小于0.01的润滑体系，但是当液体的等效黏度较大时，引起较大流体薄膜剪切摩擦力，使得液体润滑无法进入超低摩擦润滑状态.

Fig.8 The effect of liquid viscosity changes on friction coefficient evolution during running-in图8 磨合过程中液体黏度对摩擦系数演变的影响

另外，研究在磨合稳定阶段表面粗糙度对液体润滑摩擦行为的影响.在磨合稳定阶段，表面粗糙度σ∞在6～12 nm之间变化，稳定阶段液体黏度为100 mPa·s，其他参数设置和表1相同.图9所示为液体润滑的摩擦行为演变.从图中看出在磨损过程中，磨损接触表面的粗糙度降低，可减少表面粗糙峰接触，有利于润滑膜的形成，实现超低摩擦状态.而当表面粗糙度保持为12 nm时，由于液体等效黏度随时间增大到100 mPa·s，在磨合磨损过程中，提高流体动压效应，摩擦系数依然可以有效降低.尽管在这状况下没有进入到超滑状态，但是对润滑体系中的摩擦系数调控设计提出了思路.在磨合过程中，表面界面效应增强液体等效黏度从而直接影响了液体润滑体系的摩擦行为，若能有效的调控固-液界面效应，增加界面液体黏度大小，这样在一定工况下，可有效的降低摩擦系数，设计出低摩擦润滑接触副.

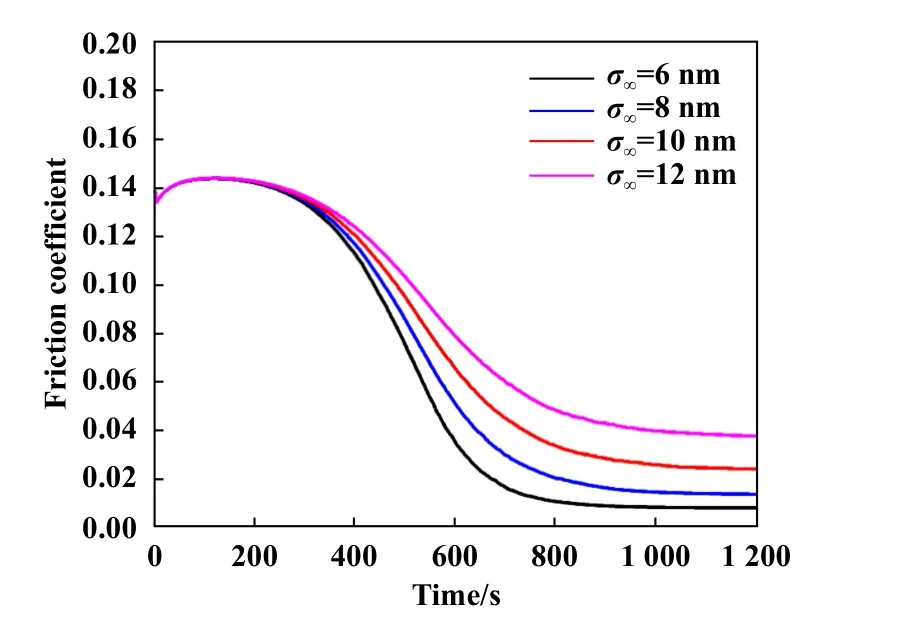
Fig.9 The effect of surface roughness on friction behavior during run-in process图9 磨合过程中表面粗糙峰对摩擦行为的影响

通过以上数值仿真结果可以发现：液体润滑经过磨合可获得超低摩擦运行状态且在此过程中呈现出典型的两个阶段即从混合润滑到液体薄膜润滑状态演变.在此过程中受到多物理因素以及时间影响，提出了磨合过程中液体黏度、表面粗糙度和磨损系数的演化式耦合流体润滑、粗糙峰接触和Archard磨损方程建立液体润滑的混合模型来研究他们对液体润性能的影响，获得了磨合过程中液体润滑实现超低摩擦经历两个阶段特征仿真结果.当液体黏度过低，导致无法有效形成流体薄膜，造成表面粗糙峰边界接触，然而液体等效黏度过大会造成较大的流体黏度剪切力，润滑体系无法实现超低摩擦状态；最后在磨合过程中发生摩擦化学反应，新生成的表面粗糙度要确保能够有效降低摩擦，这些主要的影响因素还要与工况条件相适应才可以获得超低摩擦.数值结果进一步验证了所提出在磨合过程中液体润滑实现超低摩擦的混合模型有效性.以本文中所建立液体润滑的混合模型为基础，后续将进一步考虑液体润滑介质在磨合过程中不同的液体产生特定固-液界面效应对液体润滑性能以及摩擦行为的影响开展相应的研究.

4 结论

a.建立了磨合过程中耦合流体润滑、粗糙接触力学和Archard磨损方程的混合模型并引入液体黏度、表面粗糙度和磨损系数时效函数变化，提供一种数值方法研究磨合过程中液体润滑性能演化.

b.在磨合过程中，可通过摩擦化学反应和水分子蒸发致使润滑介质的等效黏度增大，提高流体动压效应，形成流体润滑薄膜，在磨合过程中润滑区从混合润滑进入到全膜润滑，在适当的工况条件下摩擦系数可以降低到小于0.01，进入液体超滑状态.

c.在磨合过程中，表面粗糙度有效降低，可避免两表面粗糙峰直接接触，形成流体润滑薄膜，有效降低摩擦系数；同时有效提高表界面效应，减少边界摩擦系数，通过流体动压和界面效应协同作用，可进一步减少润滑接触区内的摩擦系数，实现超低的摩擦系数.