车轮多边形激励下高速列车制动界面摩擦学行为分析
王志伟,张 亮,莫继良*,王开云
(1.西南交通大学 机械工程学院 摩擦学研究所,四川 成都 610031;2.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
作为确保高速列车安全运营的最后一道屏障,制动系统摩擦学性能的优劣直接影响列车制动安全.随着我国高速列车服役数量与服役里程的不断增加,由高速列车制动问题引起的列车故障和运行安全问题时有发生,引起了工业界和学术界的高度重视[1].高速列车制动是通过制动盘与闸片之间的界面摩擦产生摩擦力,并传递至轮轨界面形成阻碍车辆前进的制动力实现的.因此,制动界面摩擦学行为受到轮轨激励的影响,并决定着高速列车摩擦制动的可靠性[2].
高速列车制动过程中,制动界面的摩擦学行为极其复杂且影响因素众多,受到了广泛的关注.制动工况[3]以及摩擦热、接触应力、接触面积和摩擦振动等因素[4-6]均会影响制动界面的摩擦学行为.因此,充分认识高速列车制动界面摩擦学行为并掌握其关键影响因素,进而改善列车制动性能是研究的热点和难点.
目前国内外研究人员通过试验测试和仿真模拟等手段,针对高速列车制动界面的摩擦学行为开展了大量研究.Xiang等[7]基于高速列车制动性能模拟试验台进行了拖曳制动试验,研究了六边形摩擦块在不同安装方向下制动系统的摩擦学行为.高飞等[8]利用ABAQUS建立了制动系统有限元模型,并结合制动试验研究了不同摩擦块形状对界面摩擦热的影响,发现摩擦副结构对制动界面摩擦热产生与分布的影响程度与制动条件密切相关.杨智勇等[9]考虑了系统的热机耦合作用,能够真实反映制动过程中温度场和应力场的分布情况,采用弹塑性热机耦合方法分析了制动盘热斑的形成.王东伟等[10]探讨了制动系统在考虑热机耦合状态下的温度分布特性,并对比分析了考虑/忽略热机耦合两种状态下系统振动信号,得出了在热机耦合状态下系统自激振动强度增大的结论.孟繁辉等[11]基于有限元软件建立了考虑制动盘表面划伤的动力学模型,分析了划伤位置、深度和缺口角度对制动过程中应力分布的影响.上述研究对制动界面摩擦学行为的认识与优化调控具有重要意义.
然而目前关于制动界面摩擦学行为的研究往往关注于制动系统本身,忽略了轮轨激励,特别是车轮多边形磨耗带来的剧烈轮轨激励的影响[12-14].在高速列车实际服役过程中,车轮多边形磨耗无法避免,且随着服役时间的增加而变得更加恶劣,这对车辆和轨道系统动态特性具有显著影响[15-16].基于高速列车制动系统的结构特性和工作原理,车轮多边形磨耗导致的高频强振轮轨激励会直接作用于制动界面并影响其摩擦学行为.目前关于车轮多边耗激励下的高速列车制动界面的摩擦行为尚不明确且有待进一步深入研究.
为解决上述不足,本文中以某型高速列车制动系统为研究对象,聚焦车轮多边形激励下的制动界面摩擦学行为,提出一种考虑轮轨激励的制动界面摩擦学行为分析方法.基于此,研究车轮多边形磨耗对制动界面摩擦学行为的影响机制.进一步,从时域和频域的角度探究不同车辆运行速度下车轮多边形激励对制动系统动态接触、温度以及振动等摩擦学行为的影响规律.
1 高速列车制动界面的摩擦学行为分析模型
1.1 刚柔耦合车辆动力学模型
1.1.1 柔性轮对模型
为了更加准确地反映车轮多边形激励引起的轮对弹性变形对制动系统的影响,需建立柔性轮对动力学模型.对于柔性轮对上任意一点P,其位移矢量r可表示为[17]
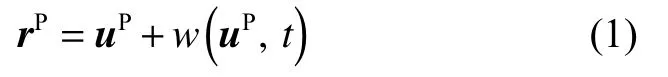
式中:uP是轮对P点在固定坐标系下的刚体位移矢量,w(uP,t)是P点在t时刻的弹性变形,可通过模态叠加法获取:
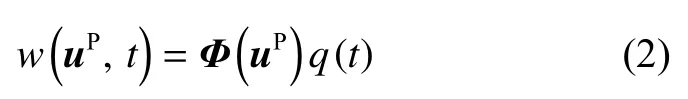
式中:Φ(uP)是轮对模态函数矩阵,q(t)是轮对模态坐标.将模态结果带入到轮对的位移矢量描述方程,基于第二类拉格朗日方程可得:
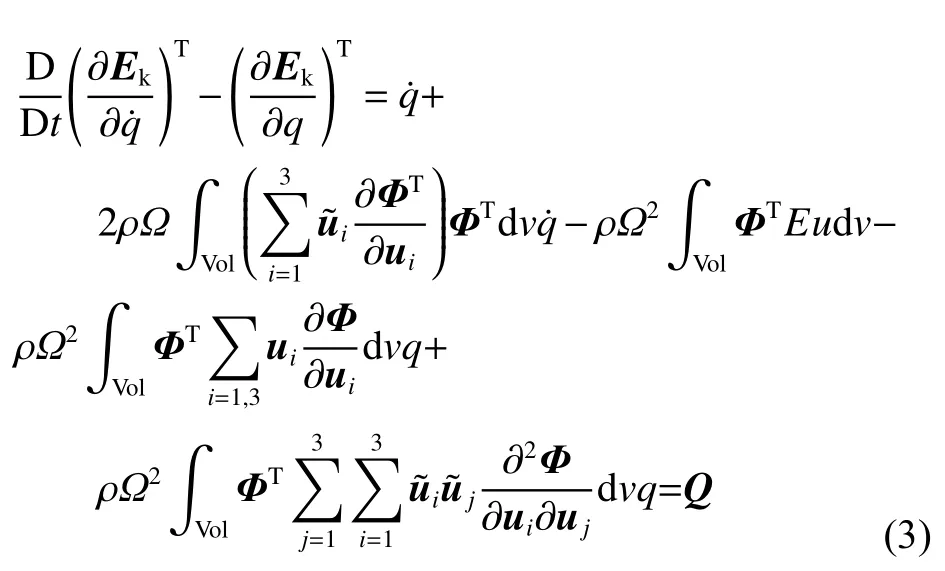
式中:D表示微分符号,Ek是系统动能,是模态坐标对时间的一阶导数,ρ表示密度,ΦT是轮轨模态函数矩阵的转置矩阵,E是弹性模量矩阵,u是轮对位移矩阵,下标“i”和“j”表示不同方向,dv表示单位体积,Vol表示结构总体积,符号“~”表示坐标变换.
通过有限元方法计算轮对自由模态结果,轮对动力学方程为
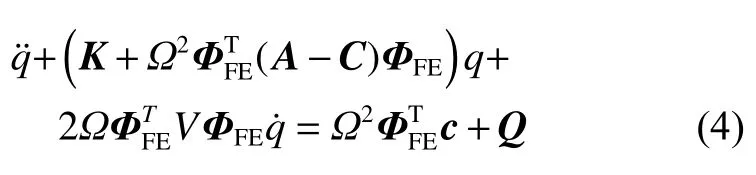
式中:是模态坐标对时间的二阶导数,Ω是轮对角速度,ΦFE是有限元计算的振型函数矩阵,上标“T”表示矩阵转置,K是无阻尼模态频率平方的对角矩阵,Q是广义力矩阵,V是科氏加速度引起的惯性力矩阵,矩阵A与相对加速度有关,矩阵C与变形后的离心力有关,c是恒定的离心力向量.
1.1.2 轮轨关系
为了更加真实地考虑轮轨作用关系,车辆动力学模型考虑轮轨空间作用关系,如图1所示.采用Hertz非线性弹性接触理论,轮轨之间的垂向力P(t)可通过式(5)计算[16].
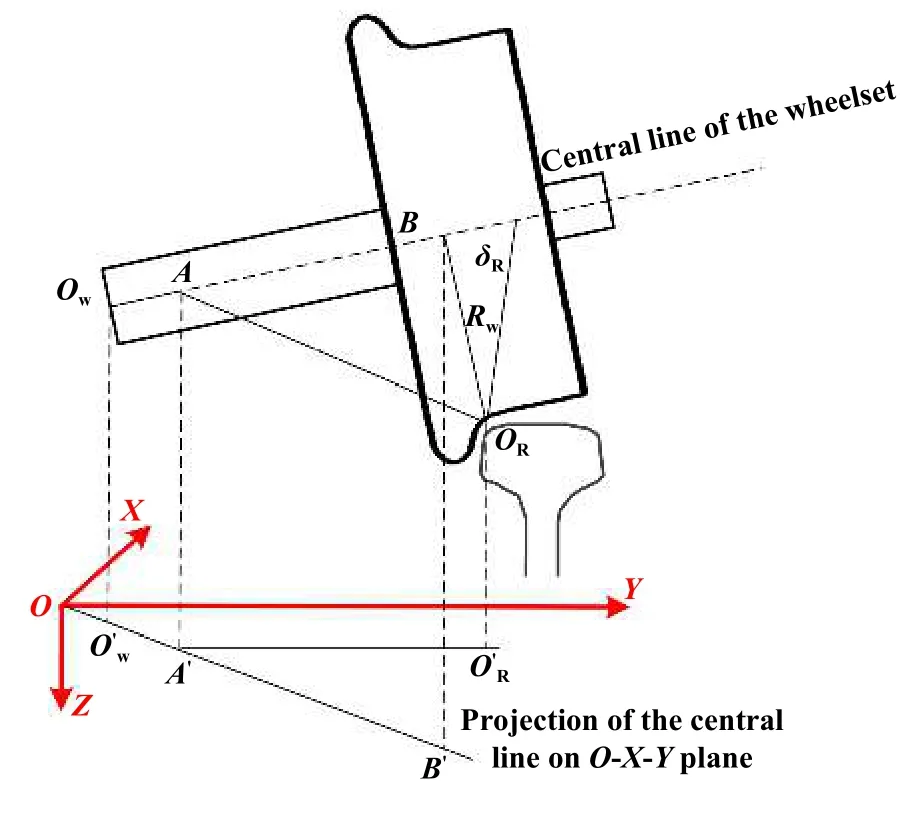
Fig.1 Wheel-rail contact relationship图1 轮轨接触关系
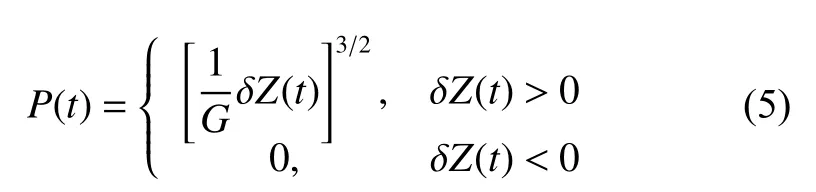
式中:G是轮轨接触常数,由车轮与钢轨几何参数决定;δZ(t)是轮轨间法向压缩量.采用迹线法可计算左右两侧车轮对应的轮轨接触位置及压缩量,左右两侧轮轨法向压缩量可表示为

式中:下标“L”和“R”分别表示左侧和右侧,ZLWj0和ZRWj0表示初始时刻第j位轮对左右两侧轮轨最小垂向间距,ΔZLWj和ΔZRWj表示当前时刻第j位轮对左右两侧轮轨最小垂向间距,δL和δR是左右两侧车轮踏面接触角,δZWj是当前时刻第j位轮对质心的垂向位移,φW是轮对侧滚角.基于轮轨接触位置并采用Kalker线性蠕滑理论,轮轨纵向蠕滑力Fx、横向蠕滑力Fy和蠕滑力矩Mz可表示为[18]
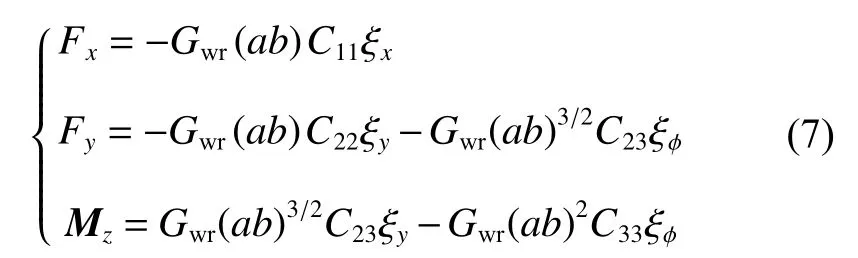
式中:Gwr是轮轨材料的合成剪切模量;a和b分别为接触椭圆的长半轴和短半轴,Cij是拟合系数,取决于接触椭圆长短半轴之比,下标i和j表示方向;ξx、ξy和ξφ分别表示纵向、横向和自旋蠕滑率.由于Kalker线性蠕滑理论仅适用于小蠕滑率和小自旋情况,采用如下非线性修正,可适用于任意蠕滑率值和小自旋值情况[19]:
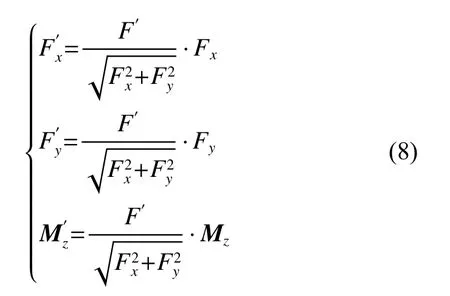
式中F'x、Fy'和Mz'分别表示为修正后的纵向蠕滑力、横向蠕滑力和蠕滑力矩,其中
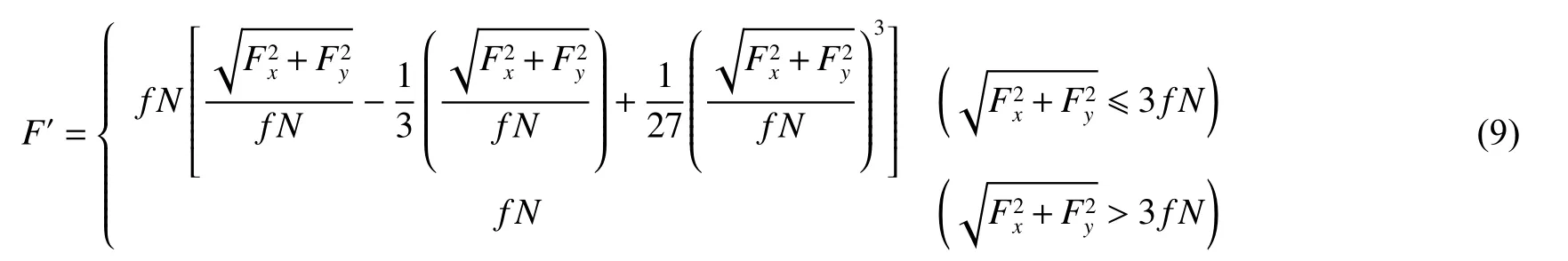
式中:f表示轮轨摩擦系数,N为接触点法向力.
1.1.3 车辆系统动力学模型
基于多体动力学理论,并结合上述柔性轮对模型与轮轨关系,建立考虑轮对柔性变形的刚柔耦合车辆系统动力学模型,系统的动力学方程为
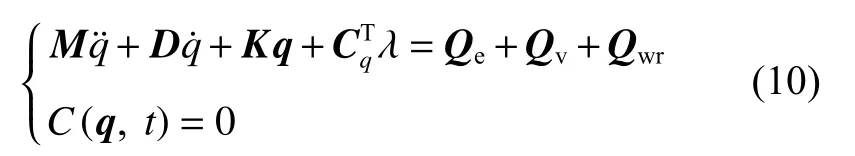
其中:M为系统质量矩阵;D为 阻尼矩阵,K为刚度矩阵,q、和为系统广义坐标向量及其关于时间的一阶和二阶导数,为系统雅克比矩阵的转置矩阵,λ为拉格朗日乘子;Qe为广义外力向量;Qv为广义惯性力向量;Qwr为轮轨力广义向量;C(q,t)为系统约束方程.该模型考虑了车体、构架、轴箱和轮对等关键部件.基于高速列车的结构特性,各部件通过铰接、一系和二系悬挂相互连接,同时考虑了车辆横向止挡、垂向减振器和抗蛇行减振器等非线性特性.车辆动力学模型的具体推导可参考前期工作[17,20],这里不再重复介绍.
1.2 制动系统热机耦合模型
基于制动系统缩比试验台制动盘和摩擦块几何模型,建立简化的制动系统有限元模型,主要由制动盘、摩擦块和夹具组成,如图2所示.制动盘和摩擦块材料与实际服役高速列车制动系统材料一致.在有限元模型中,制动盘孔的内表面耦合到参考点RP1,通过参考点RP1给制动盘施加绕Z轴的转速.两侧夹具的两端孔内表面分别耦合到参考点RP2和RP3,并通过参考点RP2和RP3来分别给制动盘施加沿Z轴方向两侧的制动力.设置制动盘和摩擦块为面-面接触,摩擦块与夹具之间设置绑定约束.制动系统各部件材料参数列于表1中.

表1 制动系统材料参数Table 1 Material parameters for brake system
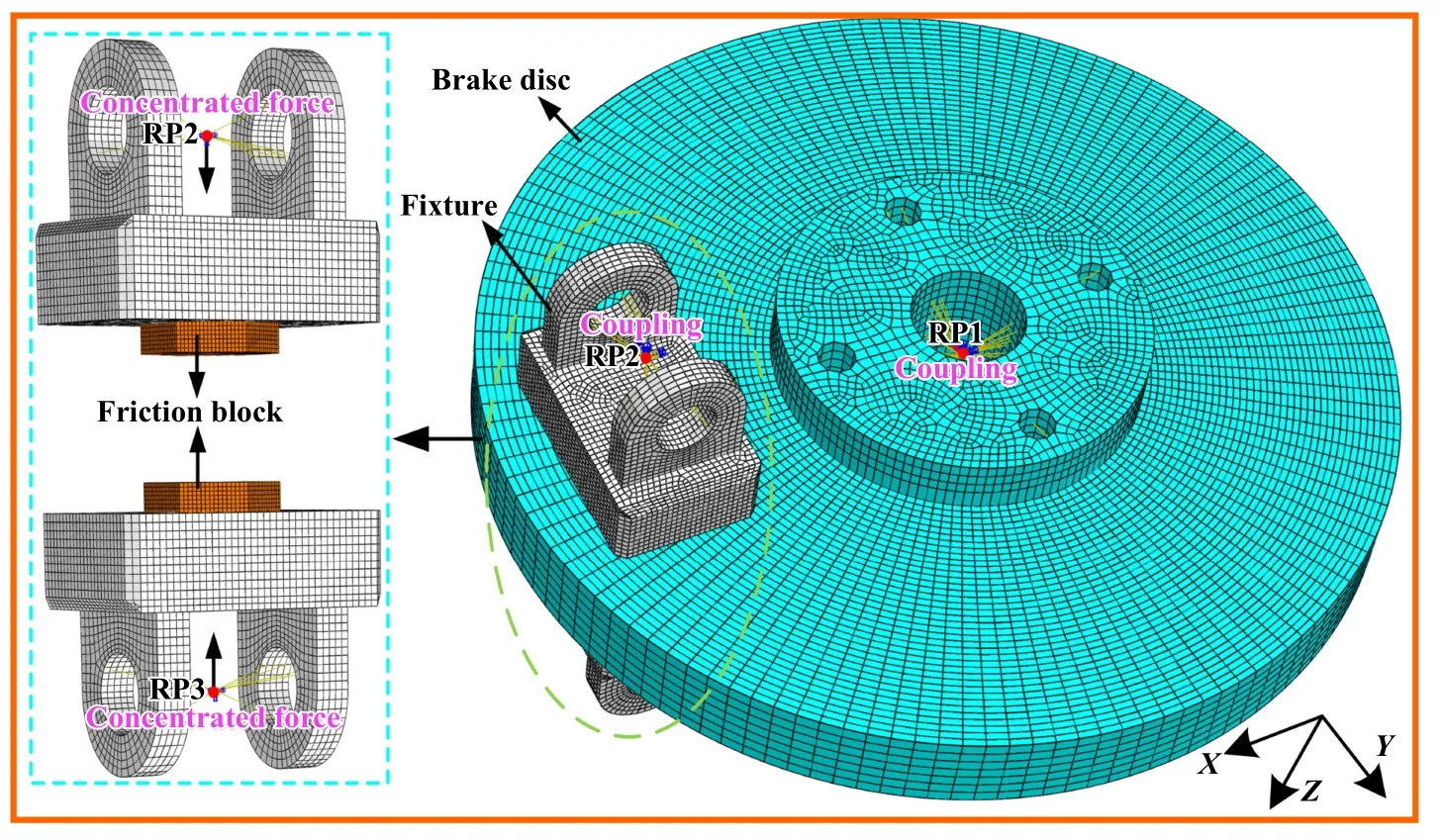
Fig.2 Thermo-mechanical coupling model of the brake system图2 制动系统热机耦合模型
建立的制动系统热机耦合有限元模型详细考虑制动盘与制动块摩擦接触过程.在此基础上,基于热力学原理,考虑服役过程中制动盘与摩擦块摩擦生热过程.此外,在仿真过程中还考虑了热交换的影响,主要包括热传导、热对流和热辐射等.对应的参数通过台架试验进行获取与标定.需要说明的是,在装配过程中,摩擦块和制动盘之间可能存在一定的装配误差,可能会导致接触的不均匀性.因此,后续开展了相关台架试验,以验证该模型的有效性和可靠性.
1.3 制动界面摩擦学行为分析流程
为研究车轮多边形磨耗激励下制动系统的温度和振动特性,基于车辆动力学模型和制动系统有限元模型,进一步建立了考虑真实服役环境的制动系统热机耦合分析方法,如图3所示.该模型主要包括两个部分,分别是刚-柔耦合车辆动力学模型和制动系统热机耦合有限元模型.首先,基于实测的车轮多边形磨耗数据和谐波偏差法来定义车轮多边形磨耗情况,通过修改车轮名义滚动圆半径来定义车辆动力学模型中轮对多边形磨耗状态.然后,通过求解车辆系统动力学运动微分方程获取整个系统的动力学响应.基于此,获取制动系统服役过程中实际的边界条件,采用温度位移耦合瞬态隐式求解算法,并在每一步计算中通过插值的方式将振动边界施加于热机耦合有限元模型,以实现轮轨激励的有效集成.最终,获得制动系统在车轮多边形磨耗激励下的界面摩擦学响应.

Fig.3 Analysis procedure of the braking interface tribological behaviour图3 制动界面摩擦学行为分析流程
2 模型验证
2.1 车辆动力学模型验证
为了验证车辆动力学模型的有效性,试验并获取了京沪高铁某型动车组轴箱振动加速度数据,采样频率为5 kHz,传感器测点位置见文献[16].此外,针对该型高速列车车轮磨耗情况进行了测试,获取车轮镟修前车轮多边形磨耗数据.现场测试情况如图4所示,结果表明某型高速列车车轮的20阶多边形磨耗问题最突出[16].
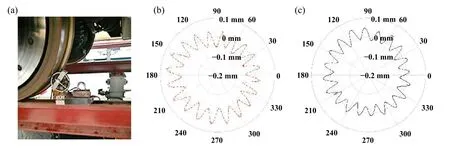
Fig.4 Wheel polygonal wear test: (a)field tests,(b)left wheel,(c)right wheel图4 车轮多边形磨耗检测:(a)现场测试;(b)左侧车轮;(c)右侧车轮
为了验证车辆系统动力学模型,将实测车轮多边形磨耗数据通过函数形式作为输入,并通过数值仿真获取轴箱振动加速度信号.仿真工况与试验条件保持一致,即车辆在直线轨道上运行,且运行速度为300 km/h.仿真与试验获得的轴箱的振动加速度结果如图5所示.图5(a)表明,试验所得轴箱振动加速度幅值略大于仿真结果,两者基本吻合,这种误差主要是由动力学模型建立过程中忽略了包括轨道等关键结构的柔性变形,且线路不平顺激励也无法完全一致引起的[12,20].图5(b)表明,试验和仿真得到的轴箱振动加速度主频均为574.5 Hz,与时速300 km/h运行时20阶多边形车轮的激励频率576 Hz接近.总体来说,仿真与线路试验结果具有较好的一致性,表明建立的刚柔耦合车辆动力学模型能够比较准确地揭示车辆系统的振动特性.
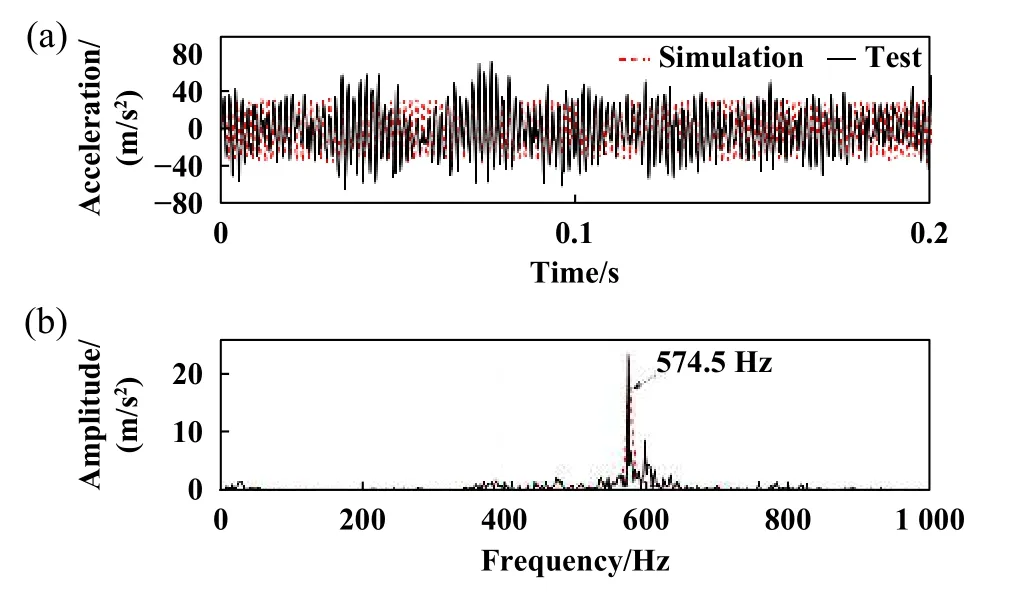
Fig.5 Results comparison of the simulated and tested axlebox vibration acceleration: (a)Time history curve;(b)frequency results图5 仿真与试验轴箱振动加速度结果对比:(a)时间历程曲线;(b)频谱结果
2.2 制动系统有限元模型验证
为验证制动系统有限元模型的正确性,基于自行研制的多模式车辆制动性能模拟试验台,开展拖曳制动试验.试验台示意图及样品尺寸如图6所示.试验过程中,通过热成像仪(FLIR E40,精度±2 ℃)测试摩擦块界面温度分布.通过Tactilus数据采集装置并使用SPI H-series纳米材料矩阵式压力膜传感器测试摩擦块接触压力分布情况.此外,通过加速度传感器同步采集并记录振动信号,采样频率为50 kHz.
摩擦块样品的加工材料取自高速列车制动闸片,为铜基粉末冶金.摩擦块横截面形状与我国某型动车组一致且接触面积为762 mm2.制动盘样品选用锻钢材料,摩擦块及制动盘样品的具体尺寸(单位均为mm)和接触位置如图6所示.试验过程中,环境温度为22~27 ℃,相对湿度为62%~70%.制动盘转速设置为346 r/min,对应高速列车运行速度为60 km/h,制动力为700 N,摩擦半径为120 mm.试验结束后,取试验过程中稳定阶段61~62 s夹具上的振动加速度,如图7所示.结果表明,系统切向和法向振动加速度均出现了周期性稳定振动,而且频谱图中均在13 576 Hz处出现了主频峰.
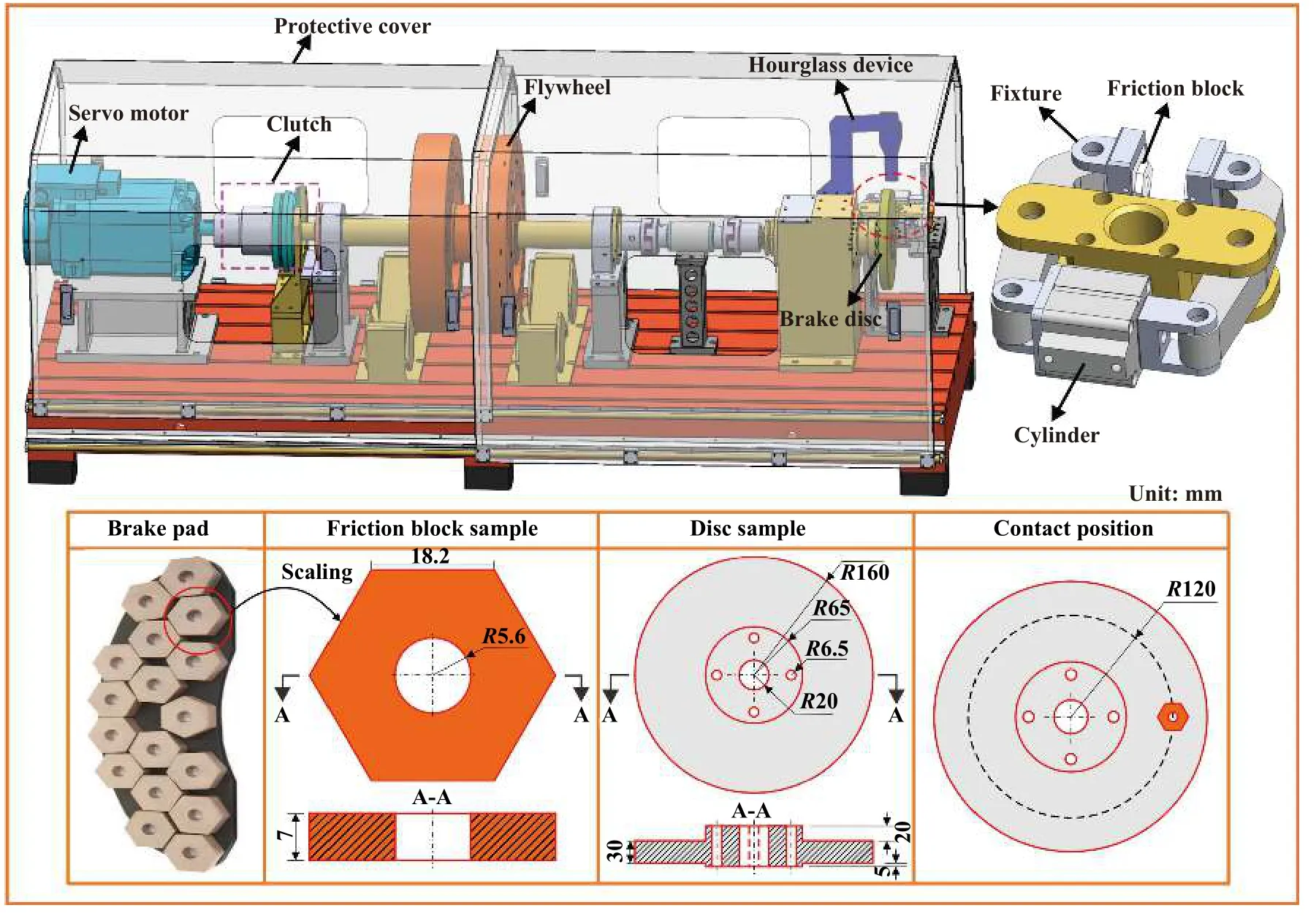
Fig.6 Schematic of the test rig and sample dimensions图6 试验台示意图及样品尺寸

Fig.7 Experimentally acquired vibration acceleration results: (a)tangential direction,(b)normal direction; (c)amplitude spectra of tangential and normal direction图7 试验获取的系统振动加速度结果:(a)切向;(b)法向;(c)频谱图
为验证制动系统有限元模型的正确性,进一步开展了复特征值分析.在复特征值分析过程中,所有部件采用C3D8R单元类型,制动力和制动盘转速与试验保持一致.另外,将制动盘与摩擦块之间的接触界面定义为摩擦接触,其接触算法为罚函数算法,滑移形式为小滑移,并分别对在0.2~0.7范围内摩擦系数进行复特征值分析.
图8(a)所示为第31阶模态和第32阶模态特征值的虚部(即系统不稳定振动频率)随摩擦系数的演化.可以看出,制动系统出现了一对耦合频率,当摩擦系数较小时,系统的相邻两阶复特征值拥有不同的虚部.当摩擦系数为0.47时,制动系统的第31阶复特征值虚部和第32特征值虚部开始收敛于1个值,表明系统发生了模态耦合,其临界摩擦系数为0.47,对应耦合频率为13 695 Hz.随着摩擦系数的增大,系统第31和第32阶模态的耦合频率并未发生明显变化.因此,复特征值分析所预测的制动系统不稳定振动频率在13 695 Hz左右,与试验得到的不稳定频率13 576 Hz基本吻合,验证了试验和仿真结果的正确性.制动系统不稳定振动模态如图8(b)所示.当系统处于不稳定振动模态时,各部件均出现了不同程度的变形.其中,最大变形位置出现在两侧摩擦块的切出端,两侧摩擦块表现出明显的对称性.以上分析表明,制动系统有限元模型的材料属性以及边界条件的设置准确有效,能够反映系统动态特性,可用于进一步的研究和分析.
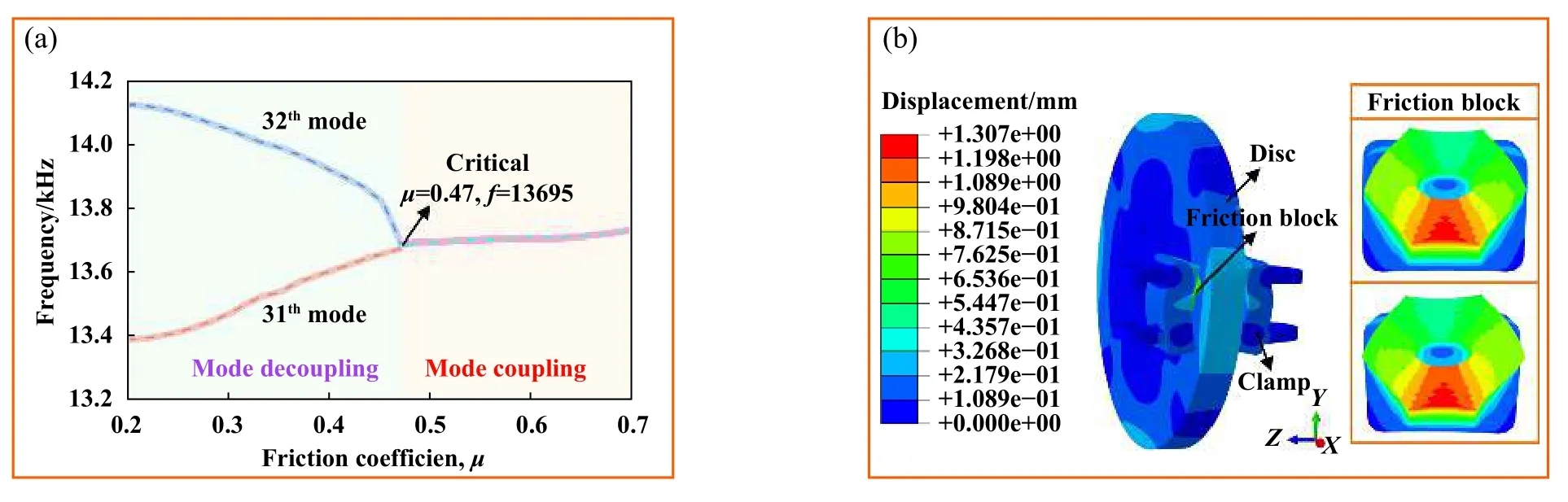
Fig.8 Simulation results: (a)complex eigenvalue imaginary part; (b)instability mode图8 仿真结果:(a)复特征值虚部;(b)系统不稳定模态
3 分析与讨论
3.1 动态接触分析
为研究实测车轮多边形磨耗对制动系统动态接触特性的影响,开展了仿真分析,盘片摩擦系数设置为0.4,车辆速度为50 km/h.对比分析有/无车轮多边形磨耗状态的同侧摩擦块接触面积和接触压力,结果如图9所示.可以看出,在多边形磨耗作用下,摩擦块接触面积和接触力的波动幅值明显增大,制动盘与摩擦块间相互接触更加复杂且不稳定.图10所示为有/无车轮多边形磨耗状态的同侧摩擦块最大接触压力云图.结果表明,车轮多边形磨耗导致制动盘与摩擦块动态接触压力增大.与无多边形激励状态相比,车轮多边形磨耗导致最大接触压力增长31.4%,且其分布更集中.
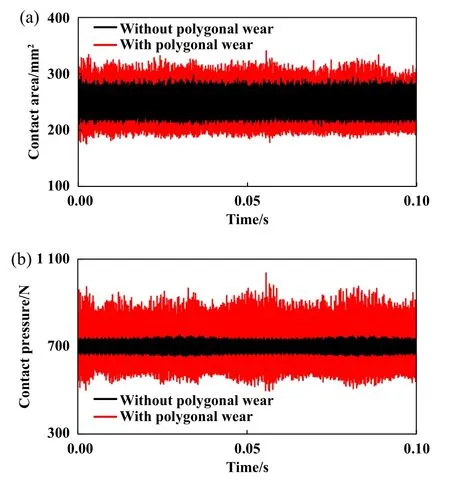
Fig.9 Contact area and contact pressure图9 接触面积和接触压力
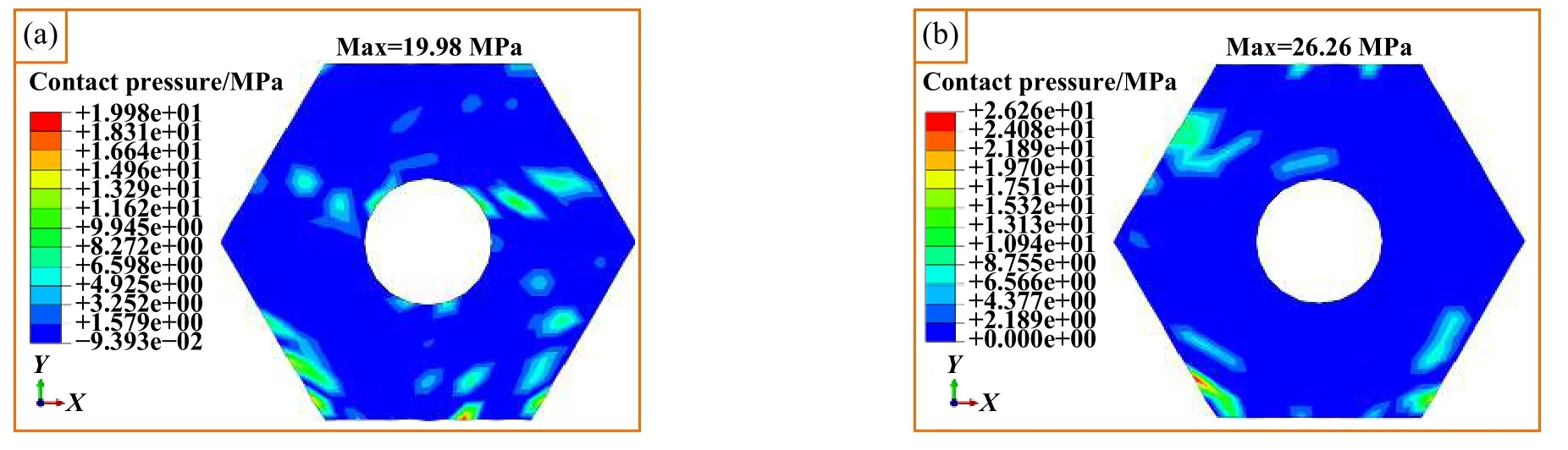
Fig.10 Contact pressure: (a)without polygonal wear; (b)with polygonal wear图10 接触压力:(a)无多边形磨耗;(b)有多边形磨耗
图11所示为有/无车轮多边形磨耗的同侧摩擦块界面温度分布情况.可以看出,两种工况下摩擦块界面高温区域均主要出现在切入端.这是由于在制动时,摩擦力引起的旋转压紧效应使摩擦块切入端成为主要的应力集中区域并产生局部高温现象.此外,实测车轮多边形磨耗导致制动系统摩擦块界面最大温度更高,且高温区域分布相对离散.因此,制动系统在实测车轮多边形磨耗状态下,局部接触行为更为突出,局部高温现象更加明显.
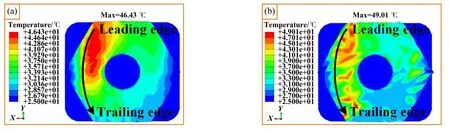
Fig.11 Temperature at the interface of friction block: (a)without polygonal wear; (b)with polygonal wear图11 摩擦块界面温度:(a)无多边形磨耗;(b)有多边形磨耗
进一步,为探究不同车辆运行速度下车轮多边形磨耗对制动系统动态接触特性的影响规律,对比分析了不同工况下摩擦块接触面积标准差和最大接触压力,结果分别如图12和图13所示.可以看出,摩擦块接触面积标准差和界面最大接触压力均随车辆运营速度的增加而增大.与无多边形磨耗的结果相比,车速从50 km/h增至300 km/h时,车轮多边形磨耗导致摩擦块接触面积分别增加了52.0%、55.2%、59.9%和84.4%;界面最大接触压力分别增加了37.1%、34.8%、36.7%和46.7%.这说明车轮多边形磨耗导致制动界面接触行为更加复杂,同时导致制动盘与摩擦块之间的动态接触力明显增大,且这种相互作用随速度的增加变得更加剧烈,增加了制动系统摩擦磨损及结构失效的概率.
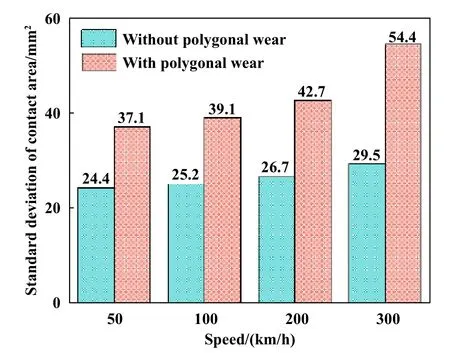
Fig.12 Standard deviation of contact area at different speeds图12 不同速度下接触面积标准差
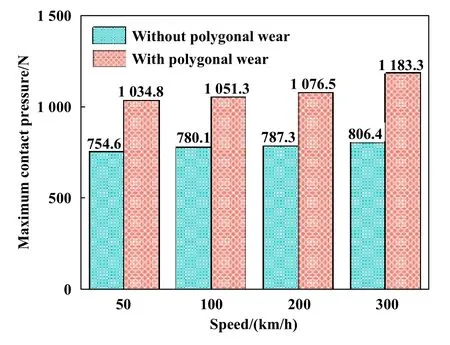
Fig.13 Maximum contact pressure at different speeds图13 不同速度下接触压力最大值
3.2 振动特性分析
为了研究实测车轮多边形磨耗对制动界面振动特性的影响,对比分析了车速为50 km/h下有/无车轮多边形磨耗的制动盘振动加速度,结果如图14所示.结果发现,车轮多边形磨耗导致制动盘振动加速度明显增大.从制动盘振动加速度频谱图看出,两种工况下频谱图中均包含4.9 Hz的主频,这与当前速度等级下制动盘的转动频率一致.不同的是,在实测车轮多边形磨耗激励下,制动盘频谱图中出现了95和12 278 Hz的频率,其中95 Hz与当前速度下20阶车轮多边形磨耗对应的激励频率比较接近,而12 278 Hz为制动盘的模态振动频率.图15所示为有/无车轮多边形磨耗状态下摩擦块夹具振动加速度的时间历程曲线.可以看出,有/无车轮多边形磨耗状态下夹具的主频分别为10 483和10 323 Hz,与制动系统10 659 和10 303 Hz的固有模态振型对应.由此可知,实测车轮多边形磨耗能够激起系统的另一阶模态振动,进而导致振动加剧.
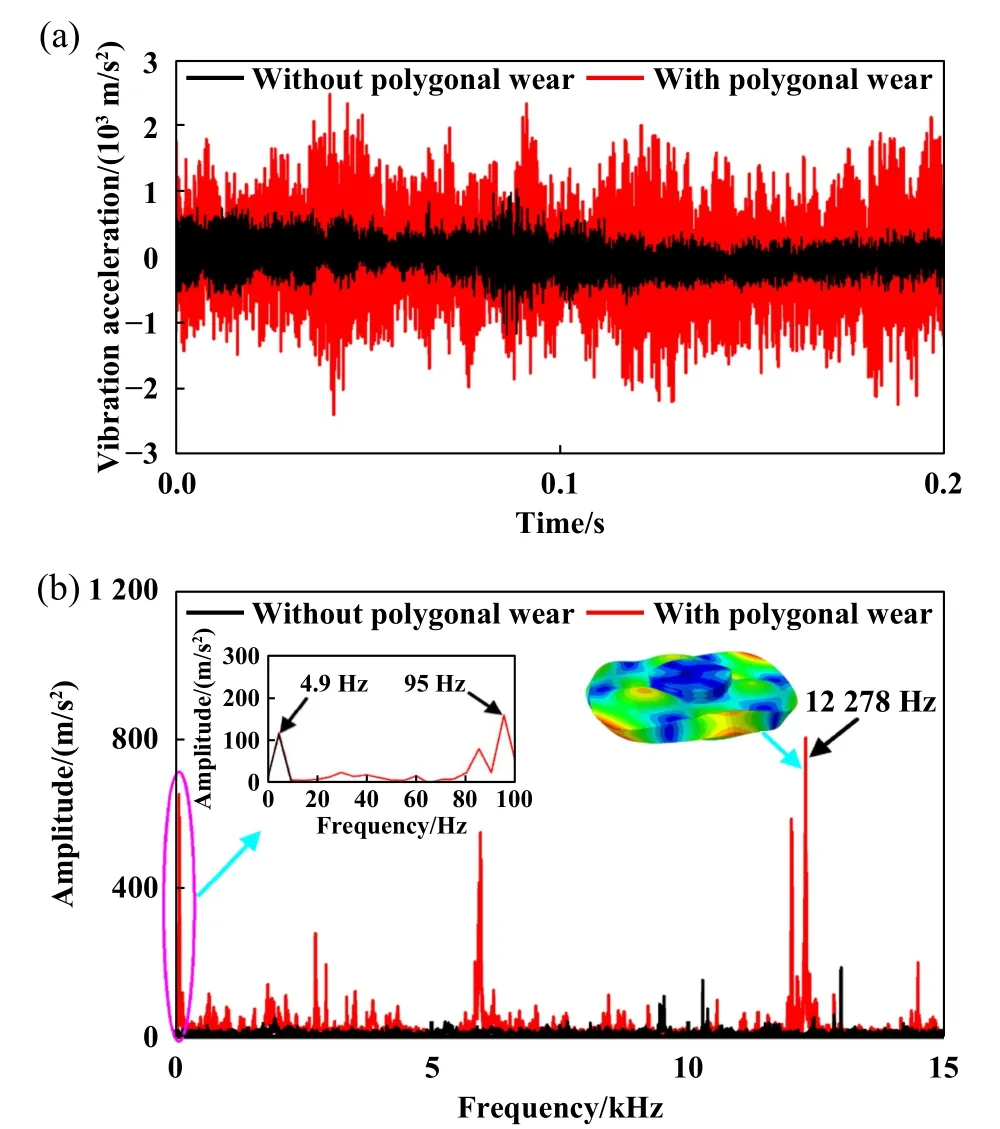
Fig.14 Time and frequency domain diagrams of brake disc vibration acceleration: (a)time domain diagram; (b)frequency domain diagram图14 制动盘振动加速度时域图及频域图:(a)时域图;(b)频域图
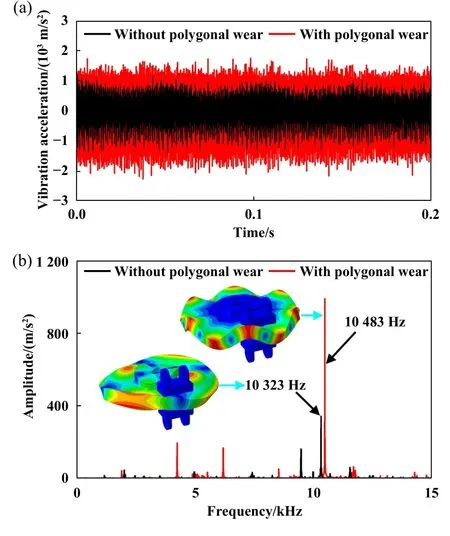
Fig.15 Time and frequency domain diagrams of the vibration acceleration of the fixture: (a)time domain diagram;(b)frequency domain diagram图15 夹具振动加速度时域图及频域图:(a)时域图;(b)频域图
图16所示为不同车辆运营速度下车轮多边形磨耗对制动系统夹具上的振动特性随速度变化情况.结果表明,系统振动加速度均方根值(RMS)随车辆运营速度的增加而增大.车速从50 km/h增加至300 km/h时,实测车轮多边形磨耗导致系统振动加速度均方根值相较于与无多边形磨耗分别增加了99.7%、92.8%、72.3%和163.7%.由此可知,服役过程中车轮多边形磨耗能够激起系统另一阶模态振动,进而导致系统振动加剧,而且系统振动加速度均方根值均随车辆运营速度的增加而不断增大.

Fig.16 Vibration acceleration of the system at different speeds图16 不同速度下系统振动加速度
4 结论
a.实测车轮多边形磨耗导致系统动态接触行为更加复杂,摩擦块界面接触面积波动幅值、动态接触力以及最大温度明显增大,且接触压力和高温区域分布更加离散.另外,制动盘与摩擦块之间的接触面积标准差和最大接触压力随速度的增加而增大,且高速条件下车轮多边形磨耗对制动界面接触行为影响更加显著.
b.与无车轮多边形磨耗相比,车轮多边形磨耗会激起制动系统某阶模态振动,且幅值更大,进而导致制动系统振动明显加剧.此外,在不同车辆运营速度下,系统振动加速度均方根值随着速度的增加而增大,高速阶段这种影响尤为突出.
c.在高速列车制动系统摩擦学行为分析中,车轮多边形激励具有较大影响.与无多边形磨耗相比,车速从50 km/h增至300 km/h时,实测车轮多边形磨耗导致系统振动加速度均方根值分别增加了99.7%、92.8%、72.3%和163.7%.为更加真实地反映实际服役过程高速列车制动系统摩擦学行为,需要考虑车轮多边形磨耗的影响.
——纪念摩擦学创始人乔斯特博士诞生100周年

