采用含22.5°二面角反射器无源定标体组的极化校准方法*

张道明，邓晓波，张 勇

(中国航空工业集团公司 雷华电子技术研究所， 江苏 无锡 214063)

极化校准技术是指通过测量极化散射特性已知的定标体求取待校准极化雷达的系统误差参数，以便对这些误差进行校正和补偿的技术[1]。根据定标体是否有源，极化校准技术可分为有源校准技术[2]、无源校准技术[3-7]以及无源和有源结合的校准技术[8]。根据所使用的定标体类型，极化校准技术可分为点目标校准技术[3-5,9-14]、分布式目标校准技术[6]以及点目标与分布式目标相结合的校准技术[7,15]三类，其中无源点目标校准技术是开展研究最早最多，应用也最为广泛的一类技术。迄今为止，人们先后提出了高极化隔离度校准算法[3]、单目标校准算法[9]、改进的三目标校准算法[10]、单二面角校准算法[11]、类点目标校准算法[12]、全极化校准算法[13]等点目标极化校准算法。这些算法要么假定待测目标具有某种特性，要么假定雷达系统的失真矩阵具有某种特殊形式，使得它们的应用受到了一定的限制。Whitt 等于1991 年提出了广义极化校准算法[14]，该算法不需要对系统失真矩阵作任何假设，用于定标的目标也只需要满足很少的限制条件，校准效果良好，因而得到了广泛应用[16-18]。

由于三面角反射器、0°二面角反射器、45°二面角反射器容易制作，因此人们常常将三者作为一组定标体对极化雷达系统进行校准。这种情况下，利用Whitt算法求解系统的失真矩阵时，往往会因特征值配对准则失效引起特征值配对错误从而导致系统失真矩阵求解错误[19]。本文就这一问题进行研究，并提出了新的定标体组和定标方法，可有效解决上述问题。

1 Whitt算法及存在的问题

1.1 Whitt算法

全极化合成孔径雷达(synthetic aperture radar, SAR)系统的极化定标模型[16]可表示为：

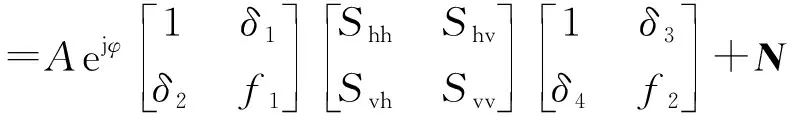
=ejφARST+N

(1)

式中，M为系统测量得到的目标极化散射矩阵，S为目标的真实极化散射矩阵，R和T分别为系统接收和发射失真矩阵，A为系统绝对幅度增益因子，φ为绝对相位，N为杂波和噪声矩阵。

采用式(1)的定标模型，考虑真实散射矩阵已知的三个不同点目标的极化测量。利用下标来区分不同的点目标和相应的散射矩阵(测量值和真实值)，可以得到三个矩阵方程：

Mk=ejφkARSkT+Nkk=1,2,3

(2)

由于各个目标的相位中心到雷达天线相位中心的距离并不相等，所以这里也用下标k来表明各个目标的绝对相位φ互不相同[16]，但由于大多数应用仅仅需要知道散射矩阵S的相对相位，所以，这里并不对这些绝对相位定标。

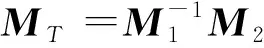
=ej(φ2-φ1)T-1STT

(3)

(4)

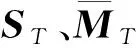
STXT=XTΛST

(5)

MTYT=YTΛMT

(6)

其中，ΛST、ΛMT分别为ST、MT的特征值构成的对角阵，XT和YT的列向量分别由ST、MT的特征向量构成。由于MT和ST为相似矩阵，因此它们的特征值与特征向量矩阵之间应有：

ΛST=ΛMTej(φ1-φ2)

(7)

YT=T-1XT

(8)

需要指出的是，给定ΛST，则ΛMT中的特征值的次序必须保证式(7)成立。

(9)

(10)

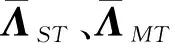
由于构成XT和YT的特征向量有任意的尺度因子，所以，由式(8)不能唯一确定T。选取尺度因子，则矩阵T可以表示为：

(11)

式中，C=diag(c1,c2)是含有未知元素c1≠0、c2≠0的对角阵。

从式(4)也可得到另一个关于T的矩阵方程：

(12)

联合求解式(11)和式(12)，即可得到发射失真矩阵T。

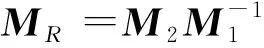
=ej(φ2-φ1)R-1SRR

(13)

(14)

采用类似求解T的方法，可以求解出接收失真矩阵R。

得到发射失真矩阵T和接收失真矩阵R后，可进一步求得系统绝对幅度增益因子A，从而实现系统的极化校准。

1.2 Whitt算法存在的问题

从式(7)～(10)可以看出，由于ST和MT的特征分解过程彼此独立，为求得T，在对ST和MT进行特征分解后，需要将两者的特征值正确配对。实际上，由于相位项φk未知，无法直接根据式(7)和式(9)进行特征值配对。为此，Whitt算法中给出了下述特征值配对准则[14]：若ΛST=diag(λST1,λST2)，并且ΛMT的两个特征值为λMT1、λMT2，则ΛMT为：

(15)

Whitt算法对定标体的要求容易验证，三面角反射器、0°二面角反射器、45°二面角反射器这一组定标体满足算法的要求，因此实际中，通常采用这样一组定标体对系统进行极化校准。不失一般性，假设0°二面角反射器为定标体1、三面角反射器为定标体2、45°二面角反射器为定标体3，并且假设若ΛMT和ΛST的特征值的次序是对应的，则

(16)

因此有

(17)

此外，由于

(18)

容易知道，ST的特征值为-1、1，因此同样有

(19)

特征值无法正确配对将导致最终求解得到的发射失真矩阵T和接收失真矩阵R错误，具体情况可见文献[19]。

通过上文分析可知，出现配对错误问题的两个原因同时存在：①式(3)和式(4)中的定标体的观测矩阵中的绝对相位项φ1、φ2、φ3与各个目标的相位中心到雷达天线相位中心的距离有关，无法直接精确测出，为未知项；②利用三面角反射器、0°二面角反射器、45°二面角反射器定标体组基于Whitt算法进行定标时，涉及矩阵的特征值模值相同，相位相差π，这导致无论如何配对，均满足式(7)和式(9)的约束。

2 极化校准方法

基于上文分析，本部分考虑利用极化散射矩阵测量值与极化散射矩阵真值之间的关系，得到各定标体回波信号绝对相位近似为0时的极化散射矩阵测量结果，从而将绝对相位未知条件下的极化校准问题转化为绝对相位近似已知条件下的极化校准问题，实现对系统极化失真的校准。为此，本部分提出了新的定标体组，并基于Whitt算法，提出新的点目标极化校准方法。

2.1 定标体

使用三种定标体作为一组进行极化校准，分别为0°二面角反射器、三面角反射器或者金属球(考虑到所需的信杂比等因素，一般使用三面角反射器)、22.5°二面角反射器。

0°二面角反射器的理论极化散射矩阵为：

(20)

三面角反射器的理论极化散射矩阵为：

(21)

22.5°二面角反射器的理论极化散射矩阵为：

(22)

容易验证，采用上述三种定标体进行定标，满足Whitt算法的所有要求。另外，22.5°二面角反射器与常用的45°二面角反射器的不同之处仅仅在于二面角反射器在垂直入射波平面上的横滚角由45°变为22.5°，即只存在摆放姿态的区别，除此之外，定标体的布放方法与原有的布放方法完全相同，因此采用这样的定标体组并不会带来新的难度。

2.2 极化失真矩阵求解算法

考虑发射失真和接收失真。将式(20)代入式(2)，可知实际测量得到的0°二面角反射器的极化散射矩阵为：

(23)

由于信杂噪比较大，忽略杂波和噪声，则可知当其绝对相位φ1为0时，

M′1=e-jφ1M1

=A1RS1T

=ejΔφ1M″1

(24)

式中，A″1为正实数，且

(25)

另外，由于δ1、δ4均较小，容易知道Δφ1≈0。

类似地，对于三面角反射器，当绝对相位φ2为0时的极化散射矩阵测量值为：

M′2=e-jφ2M2

=ejΔφ2M″2

(26)

式中，Δφ2≈0，A″2为正实数，且

(27)

对于22.5°二面角反射器，经过类似的推导，可知当其绝对相位φ3为0时，

M′3=e-jφ3M3

=ejΔφ3M″3

(28)

且Δφ3≈0。从这里可以看出，采用22.5°二面角反射器的原因在于可以利用其极化散射矩阵的特点以及失真矩阵交叉极化电平较小的特点，根据其极化散射矩阵测量值M3得到绝对相位φ3近似为0时的极化散射矩阵测量值M″3，从而利用M″k、Sk将绝对相位未知条件下的极化校准问题转化为绝对相位近似已知条件下的极化校准问题，实现系统的极化校准。

忽略杂波和噪声，考虑到

M′k=ARSkT

(29)

以及M′k=ejΔφkM″k，容易知道M″k满足：

M″k=e-jΔφkARSkT

(30)

因此，基于M″k，Sk即可利用Whitt算法进行求解。

令

=ej(Δφ1-Δφ2)T-1STT

(31)

(32)

以及

STXT=XTΛST

(33)

M″TYT=YTΛ″MT

(34)

其中，ΛST、Λ″MT、XT、YT与上文的定义类似，则M″T和ST的特征值与特征向量矩阵之间应满足：

ΛST=Λ″MTej(Δφ2-Δφ1)

(35)

YT=T-1XT

(36)

不同的是，此时Δφk≈0，因此Δφ2-Δφ1≈0，这意味ΛST、Λ″MT中的特征值正确配对时，对应特征值之间的相位差应该接近于0或很小。另外，定标目标的定向误差对其散射矩阵特征值幅度的影响远大于对其相位的影响[14]，从而很容易对ΛST和Λ″MT中的特征值进行正确配对，具体准则如下：若ΛST=diag(λST1,λST2)，并且Λ″MT的两个特征值为λMT1、λMT2，则Λ″MT为：

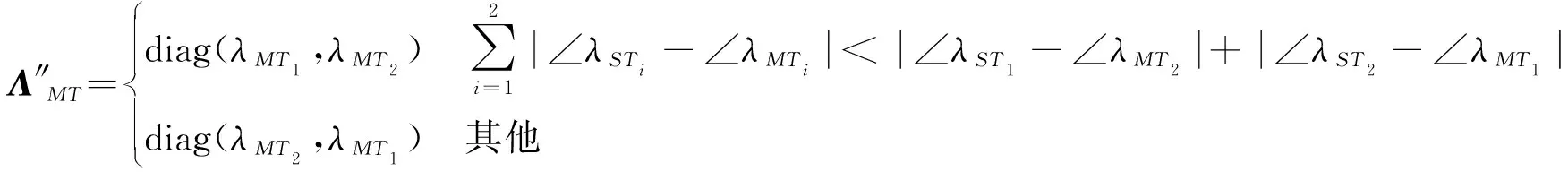
(37)

其中，∠λSTi、∠λMTi分别为复数λSTi、λMTi的相角，i=1,2。其他三组矩阵对的特征值配对情形与此类似，不再赘述。特征值正确配对后，即可按照Whitt算法求解失真矩阵T和R。

综上，所提出的极化校准方法步骤如下：

步骤1：选用0°二面角反射器、三面角反射器(或与三面角反射器归一化极化散射矩阵相同的定标体)、22.5°二面角反射器为定标体；

步骤2：对实测的Mk(k=1,2,3)进行相位补偿，得到M″k(k=1,2,3)，使得M″1(1,1)为负实数，M″2(1,1)为正实数，M″3(1,1)为负实数；

步骤3：基于M″k和Sk(k=1,2,3)，利用Whitt算法求解发射失真矩阵T和接收失真矩阵R，其中根据式(37)准则进行特征值配对。

2.3 稳健性分析

根据式(3)～(4)、式(13)～(14)、式(20)～(22)，容易知道：

(38)

(39)

(40)

(41)

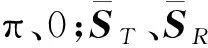
3 仿真试验结果及分析

i,j=h或v

交叉极化电平为-25 dB时，相应的发射失真矩阵为：

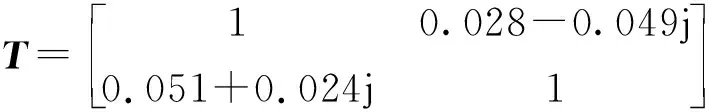
接收失真矩阵为：

摆放误差角为0°、信杂比为35 dB时，蒙特卡洛仿真试验中某次校准得到的系统发射失真矩阵和接收失真矩阵的定标结果为：

此时：

其中，幅度相对误差和相位误差的单位分别为dB和(°)。可以看出，本文算法计算出的失真矩阵与预设失真矩阵对应元素间的幅度和相位误差都很小。由于发射和接收失真矩阵的估计误差对极化散射矩阵校准结果为乘性影响，接下来利用上文设置的目标极化散射矩阵通过蒙特卡洛仿真试验验证所提方法的性能。

图1为交叉极化电平为-25 dB、信杂比为35 dB时，校准方法在不同角度误差下的仿真结果。作为对比，图1中也给出了理想情况下的仿真结果。这里所说的理想情况是指定标体摆放不存在误差，并且每个定标体极化散射矩阵测量结果中的绝对相位已知，定标体极化散射矩阵测量值仅受杂波和噪声的影响，这种情况下， 校准算法总是能够正确地进行特征值配对，从而进行校准。另外，图1中也给出了Whitt校准算法的校准结果。可以看出，随着定标体摆放误差角的增大，本文方法和Whitt算法校准后，最大幅度相对误差和最大相位误差均变大。本文方法在摆放误差角度小于1°时，其校准性能与理想情况下的校准效果无明显区别。此外需要说明的是，本文方法是与理想的无任何摆放误差时的校准结果对比，当摆放误差角度超过1°时，校准误差变大的原因在于此时的定标体及相应的散射矩阵真值已经变化，而一般情况下，极化校准方法都需要利用对定标体极化散射矩阵的敏感性实现校准，因此上述结果并非本文校准方法本身的原因所致。实际校准时，往往通过测量定标体的摆放姿态以及飞机的位置、姿态数据对摆放误差角进行补偿，从而得到准确的校准结果。

(a) 最大幅度相对误差(a) Maximum magnitude relative error

图2为定标体角度误差为0.5°、信杂比为35 dB时，校准方法在不同交叉极化电平条件下的校准结果。可以看出，对于每一种校准方法，交叉极化电平均不会明显影响其性能。另外，无论是最大幅度相对误差还是最大相位误差，本文方法与理想情况下的校准效果均无明显差别，而Whitt方法的校准性能则明显比本文方法和理想情况下的校准效果差，其根本原因在于绝对相位未知使得特征值配对问题欠定，并且基于上文所述的常用定标体定标时，两个特征值又比较特殊，从而导致Whitt方法所提出的配对准则失效。本文方法基于定标体的理论极化散射矩阵对其极化散射矩阵的测量值进行了预处理，得到了绝对相位接近0(Δφk≈0)时的极化散射矩阵测量值，等效于测出并补偿了各个定标体的绝对相位，从而可以利用所提出的相位判别准则对特征值进行配对，避免了Whitt方法中绝对相位未知导致的特征值配对错误的情况，使得本文方法能够对发射、接收极化失真进行准确校准。由于实际系统中，极化失真矩阵的交叉极化电平通常小于等于主极化电平(10 dB)，因此，经过预处理后，Δφk≈0这一结论显然成立。

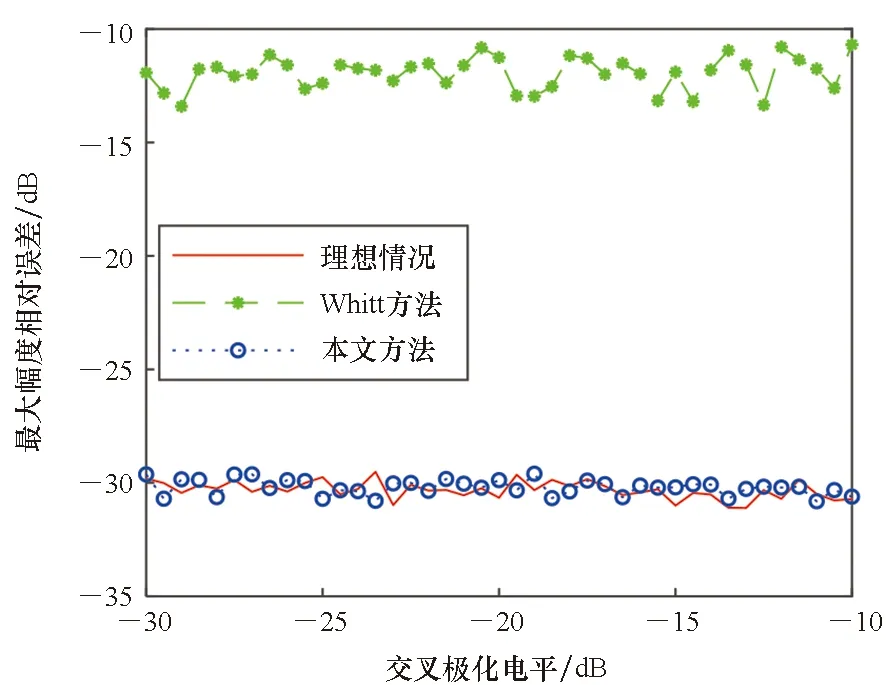
(a) 最大幅度相对误差(a) Maximum magnitude relative error

图3为定标体角度误差为0.5°、交叉极化电平为-25 dB时，不同信杂比条件下校准方法的校准效果。从图3(a)中可以看出，三种方法的最大幅度相对误差均会随着信杂比的提高而减小，并且，本文校准方法与理想情况下的校准结果无明显区别，明显优于Whitt校准方法的校准效果。从图3(b)中可以看出，本文方法与理想情况下的校准结果相同，但不同信杂比下，Whitt校准方法校准后的相位误差无明显区别，均远大于理想情况下的校准结果及本文方法的校准结果，这一结果仍然是由特征值会错误配对所致。

(a) 最大幅度相对误差(a) Maximum magnitude relative error

综合上述仿真结果及分析可以看出，本文方法在绝对相位未知的情况下，可对系统的发射接收极化失真进行校准，性能与理想情况下的校准结果一致。之所以如此，其根本原因有二：①尽管绝对相位未知，但本文方法通过对定标体极化散射矩阵测量值进行预处理，可以得到绝对相位接近于0时的极化散射矩阵测量值，从而将绝对相位未知条件下的特征值配对这一欠定问题转换成绝对相位接近于0时的特征值配对问题，在这一基础上，通过简单的相位匹配准则对特征值进行配对，即可对极化失真进行校准；②绝对相位只影响特征值的配对结果，在特征值正确配对的情况下，各个定标体的绝对相位的具体数值对定标结果无任何影响。因此，本文方法进行的预处理尽管没有得到绝对相位为0时的极化散射矩阵测量结果，但这一预处理不但给后续的特征值配对带来便利，而且不会对最终的校准结果带来任何不利影响。

4 结论

为解决利用常用定标体组基于Whitt算法进行极化校准时，算法中的特征值配对准则失效从而可能导致极化校准结果错误的问题，本文提出了新的定标体组及相应的校准方法，并通过仿真试验分析了校准方法在不同定标体角度误差、不同交叉极化电平、不同信杂比条件下的校准效果，结果表明，本方法具有良好的校准性能。由于本文所提出的新的定标体组与常用的定标体组相同，只有一种定标体存在摆放角度的区别，因此，新的校准方法同样具有广泛的适用性。