双二体几何切面法及天梯地月转移轨道分析*

童科伟，程炳琳，汪小卫

(1. 中国运载火箭技术研究院 研究发展部， 北京 100076; 2. 中国运载火箭技术研究院， 北京 100076)

双二体轨道拼接设计方法在月球探测轨道设计中具有基础性作用，国内外学者以双二体轨道拼接法为基础对月球探测轨道设计方法进行了大量的研究[1-8]。

在基于双二体问题求解地月转移轨道时，Battin、郗晓宁、黄文德、贺波勇等都不约而同地以入口点月心经纬度作为中间变量来拼接地球影响球内飞行轨道和月球影响球内飞行轨道[1-2,4-5,8]。这种基于月球影响球球坐标来描述入口点位置的方法比较直观，但是没有充分利用转移轨道的物理意义。

对于着陆地点已知的奔月任务，贺波勇推导了一种类解析的改进双二体模型，该方法与传统的从地球计算到月球不同，在计算窗口时针对已知的月心轨道六根数逆向计算地月转移轨道六根数，计算量极小[9]。

对于工程约束不明、具体探测地点不定的地月转移轨道窗口计算问题，还需要按照传统的计算量较大的搜索方法，进而得到一些运动特性。与常规的以入口点月心经纬度作为中间变量的双二体拼接方法不同，本文提出一种直接基于轨道特征的地月转移飞行轨道的几何方法，物理意义明确，求解地月轨道更加直观，通过两次降维解耦操作，降低问题求解维数，进一步提升计算效率。

考虑到目前大多数计算机都是多核中央处理器(central processing unit, CPU)，最简单的提高算力的途径是采用并行计算，充分利用各核的计算能力，并行计算技术在国内外受到高度重视。并行程序设计编程语言通常基于消息传递接口标准(message passing interface, MPI)、OpenMP等，二者甚至已经分别形成了集群并行和单机多核并行领域的事实标准[10-13]。

本文以Java相关的多核并行编程技术为基础[13]，设计了一种地月转移轨道的多核并行计算方法，并应用于天梯地月转移轨道计算与特性分析。按照国际天梯协会(international space elevator consortium, ISEC)的定义，天梯是一种把有效载荷从地球表面提升到空间的系统，该系统是一个长10万千米的绳系，质心在地球静止轨道(geostationary orbit, GEO)，并固定于地表的某个锚点。随着爬升高度的变化，天梯攀爬器在电能作用下抬升高度并获得地球自转带来的圆速度，从而使有效载荷获得势能和动能[14]。由于天梯位于赤道上空，轨道倾角受限，与常规月球转移轨道设计有一定区别。本文以一种几何切面法双二体模型来分析天梯发射航天器进入月球转移轨道的特性。

1 双二体几何切面法

双二体假设下的地月转移轨道计算也称为圆锥曲线拼接法。本质上是以月球影响球为边界, 将轨道分成多段来拼接：进入影响球前, 飞行轨迹为地心圆锥曲线(一般为椭圆)；在影响球内，飞行轨迹为月心圆锥曲线(一般为双曲线)。对于自由返回轨道等任务，还需考虑飞出影响球后的飞行轨迹，其为地心圆锥曲线(一般也为椭圆)。在进入和离开影响球的两个边界点(一般称为入口点和出口点)，将这几段圆锥曲线拼接成完整的运动轨迹。

圆锥曲线拼接法的设计参数通常以月球影响球入口点/出口点在月心白道坐标系下的经纬度作为独立变量，通过该经纬度来描述入口点/出口点的空间位置[1-2,4-6,8]。

采用传统的圆锥曲线拼接法的设计参数计算转移窗口时问题待求解参数的维度大，计算转移窗口时的计算时间过长。对于在天梯系统出发这一类地月转移轨道设计问题，由于出发轨道的倾角已知、升交点赤经(right ascension of ascending node, RAAN)也可求出，本文借助空间几何关系把原始问题降维，从而大大降低求解问题的规模。其基本思想是：基于转移轨道面和月球影响球的几何关系来描述空间位置关系，地月/月地转移轨道面与月球影响球必须相交(否则一定不可能被月球捕获)。通过转移轨道面切割月球影响球形成的几何关系就可以描述地月/月地转移轨道，结合Lambert原理就可以求解出所需的转移轨道参数。这样就把原来的三维球面搜索算法降维成了二维平面内切割月球影响球形成的圆上的搜索算法。另外本文的描述方式把地月转移轨道求解问题解耦成平面内转移轨道形状计算问题以及转移轨道空间定向问题，从而大大降低了问题求解维度。

1.1 转移三角形形状计算问题

对于从天梯出发的奔月任务来说，为了扩大任务窗口，可以适当允许出发转移轨道有小倾角，以尽可能节约推进剂，比如要求i∈[-0.5°,0.5°]。由于天梯质心位于地球定点位置，相应的升交点赤经为：

Ω=Ω0+ωEt

其中，Ω0为初始点降交点赤经，ωE为地球自转角速度，t为据初始点时刻。

如图1所示，定义地心为E，月心为L，轨道面与月球影响球切割形成圆的圆心为O。转移轨道在地球近地点出发，该点定义为P，到达月球影响球的入口点A。

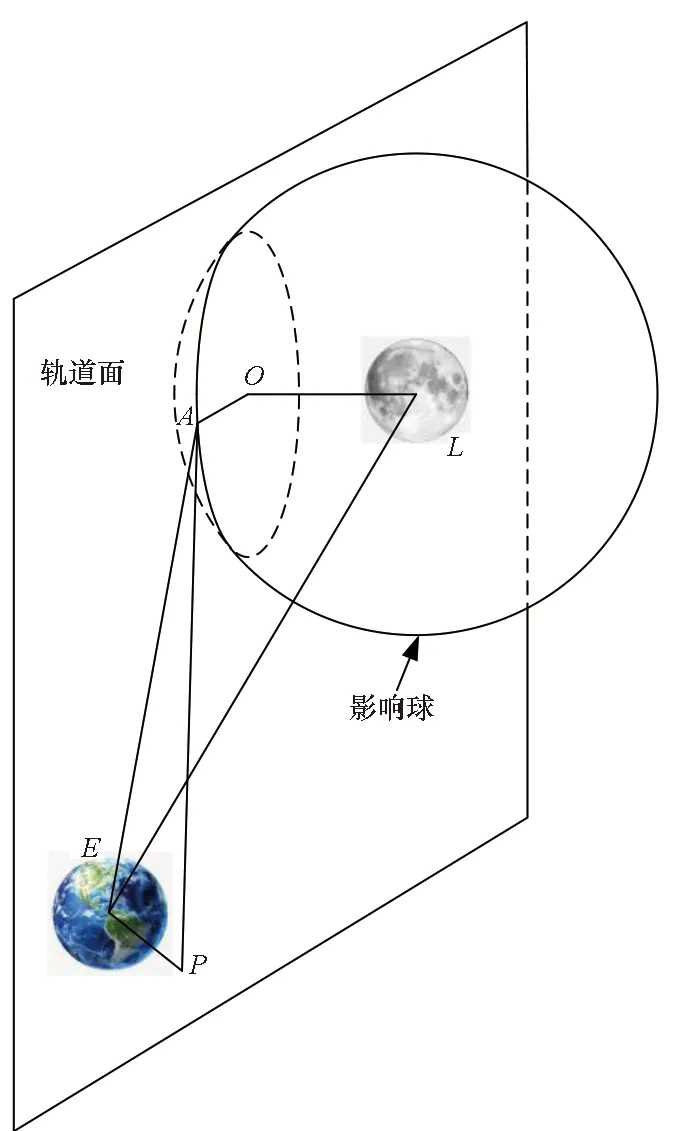
图1 轨道面与月球影响球的切割示意图Fig.1 Demonstration of section of orbital plane and the sphere of influence of moon

转移轨道面与月球影响球切割的交线必然形成一个圆，该圆上各点到月心的距离等于影响球半径rs，rs=66 200 km。转移轨道面法方向或轨道动量矩方向nOL为：

nOL=[sinisinΩ,-sinicosΩ,cosi]T

(1)

cos∠OLE|nOL·rL|/rL

(2)

其中，rL为地月距离。

由图(1)所示的几何关系可知，顺行轨道(i,Ω)和逆行轨道(π-i,Ω+π)都满足以上几何关系(二者轨道面法向相差180°)，相应的式(2)取绝对值，可根据工程实际约束来选取。

l=rLcos∠OLE

(3)

地月转移轨道面与月球影响球必须相交，否则转移轨道与月球影响球没有交点，就无法形成环月轨道。对应的数学约束条件就是：

l≤rs

(4)

发射窗口搜索时间区间出现在满足式(4)的时间段，该约束条件可以极大地节约转移窗口的计算量。

轨道面与影响球切割而成的圆半径OA的大小r0为：

(5)

(6)

k-r0≤rEA≤k+r0

(7)

图2 轨道面与月球影响球的截面平面示意图Fig.2 Section plane of orbital plane and the sphere of influence of moon

由地月几何关系，rEA取值范围可扩大为：

rL-rs≤k-r0≤rEA≤k+r0≤rL+rs

(8)

已知地月平均距离为384 400 km，因此地月距离rL考虑一定余量就可以得到rEA的取值范围，如取余量Δ=0.1可得：

(rL-rs)(1-Δ)≤rEA≤(rL+rs)(1+Δ)

即

286 380 km≤rEA≤495 660 km

(9)

在给定时间tPA内，从近地出发点P运行到入口点A的地月转移轨道构成了一个Lambert问题。根据Lambert定理，地月转移出发点P到入口点A的飞行时间tPA仅与轨道半长轴、两点与地心距离之和rPE+rEA以及弦长rPA有关。又由余弦定理，给定rPE和rEA，则弦长rPA和真近点角θPA一一对应。因此地月转移轨道问题转化为已知tPA求θPA的问题。E、P、A确定了一个与转移轨道相关的三角形，称为转移三角形。

贺波勇推导了tPA和θPA的导数关系。将tPA作为设计变量，用牛顿迭代法求解θPA[9]。本文的算例测试发现，该方法对初值较敏感，收敛性一般，计算量较大，且计算精度也不太高，为此改用Brent法求解。

Brent法在20世纪60年代，由阿姆斯特丹数学中心的Van Wijngaarden和Dekker等研究成功，并在1973年由Brent进行了改进。该方法特别适合于求解一维非线性方程的根，而无须提供函数的导数。该方法具有超线性收敛特性，又能够保证二分法的收敛确定性。具体算法参见文献[15]。

按照Brent算法，选择tPA作为设计变量，求解θPA，二者的求解关系如下：

地月转移轨道由近地点出发，存在如下关系：

rEA=p/(1+ecosθPA)

p=rEP(1+e)

可得到：

(10)

(11)

其中：p为半通径；e为偏心率；a为半长轴。

至此由θPA、a、e不难求得转移轨道飞行时间tPA，可以将求得的tPA与给定的转移轨道飞行时间tPA0之差作为待求的一维非线性目标函数，对应的未知量θPA可由Brent法求解。

转移三角形形状求解问题在整个搜索过程中重复出现，但由本文模型的描述方式可知，该三角形与轨道倾角、升交点赤经和近地点幅角无关，因此该求解问题与整体窗口搜索算法解耦，可以把转移三角形所有可能的轨道组合提前求解出来，在接下来的窗口搜索中就只需要匹配这些已知的转移三角形，从而大大降低问题的搜索维度，节省计算量。此外转移三角形形状求解问题也从原来的三维影响球的球面经纬度搜索问题降维成为平面内圆上点的搜索问题，进一步节省了计算量。

1.2 转移三角形的空间定向问题

1)对于如近地轨道空间站出发的地月转移轨道，i和初始Ω0一般已知，则当时的Ω可由到达入口点时刻和飞行时间来决定，未知量为近地点幅角ω；

2)对于天梯奔月任务来说，天梯位于赤道上方，ω等于0°(顺行轨道)或者180°(逆行轨道)，未知量为i。

以上两种情况均可由Brent算法求解。

由地心惯性系到轨道系的坐标旋转矩阵为：

其中：Lx(ϑ)表示绕x轴旋转ϑ角度的坐标旋转矩阵；Lz(ϑ)表示绕z轴旋转ϑ角度的坐标旋转矩阵；u=ω+θ为纬度幅角，其中θ为真近点角。

地心惯性系下的入口点位置矢量rEA为：

(12)

由图1可知，rEA与月球位置矢量rL(由星历计算)及入口点到月心的矢量rLA满足如下几何关系：

rLA=rEA-rL

而rLA的大小等于月球影响球半径rs，则：

|rEA-rL|-rs=0

(13)

因此根据未知的ω或者i，由Brent算法预先判断所求区间是否有解，再求解式(13)对应的一维非线性方程的根，就可以得到满足条件的未知的ω或者i[15]。即：

1)对于i给定的转移轨道，ω∈[0°,360°]，由式(12)和式(13)，根据已知的五个轨道根数，由Brent算法求解ω；

2)对于天梯任务，i∈[-0.5°,0°]和i∈[0°,0.5°]对应的逆行和顺行轨道，同样由式(12)和式(13)，根据已知的其他五个轨道根数，由Brent算法求解i。

然后根据式(1)～(6)计算转移三角形数据库中待评估的转移三角形是否满足式(7)。

以上求解轨道面参数的过程称为转移三角形的空间定向问题。

以上求解出了地月转移段轨道六个轨道根数，还需要进一步判断该轨道进入月球影响球被月球捕获以后形成的环月轨道是否满足给定条件。此时需把地心惯性系下的入口点处的矢量rLA和vLA转换到月心白道系下[2]：

M=Lz(uL+π)Lx(iL)Lz(ΩL)

其中：M为地心惯性系到月心瞬时白道系的旋转矩阵。上式中的上标L表示月球相关的参数。

基于上式求得的月心系下的位置和速度，就可以求得月心段绕月轨道参数，之后可以判断是否满足需要的环月轨道条件，比如环月轨道高度约束等。

以上是普通地月转移轨道的求解流程。对于载人航天任务常用的自由返回轨道，可基于对称性原理，进一步求得月地转移段轨道参数，再判断是否满足载人航天任务常用的自由返回轨道约束条件，如返回地球时的近地点高度、再入角等。本文只计算一般的地月转移轨道，自由返回轨道求解的具体流程可参考Battin[1]、黄文德[4-5]、贺波勇[8]等的报道。

2 天梯奔月解法

2.1 CPU并行计算技术简介

当前CPU主频的提升已经明显遇到了瓶颈，计算机硬件界主要关注如何发展多核CPU。目前民用CPU已经拥有十多个核心。针对CPU核心数越来越多的现状，科学计算必须考虑并行/并发程序设计，避免浪费计算资源。

并行计算一般可分为计算密集型、数据密集型、网络密集型[10]，本文主要关注计算密集型计算。1994年诞生的MPI已经成为集群并行程序设计事实上的标准。1997年诞生的OpenMP已经成为单机多核并行事实上的标准[10]。本文的并行程序主要针对单机多核并行架构，而单机多核图形处理器(graphics processing unit, GPU)加速并行架构和多机多核并行架构不在本文考虑。常用的并行分解技术有两种：递归分解和数据分解[11-12]。本文着重关注单机CPU并行程序设计，并主要采用数据分解的方式来设计并行程序。

本文综合考虑到可移植性、编程方便性、程序稳健性等，避免采用复杂的MPI，而是采用Java语言，并行计算程序设计基于Parallel Java 2 Library(PJ2库)[13]。

PJ2库是RIT(Rochester Institute of Technology)的Kaminsky教授开发的Java语言的并行计算调度库，并应用于RIT计算机学院的超级计算机集群上。其主要设计思想是简化并行计算程序设计的难度，特别是避免使用复杂的MPI，能够极好地适用于单机CPU、GPU并行以及分布式集群异构并行计算。PJ2库有五种CPU核心并行调度机制：Fixed、Leapfrog、Dynamic、Proportional、Guided。后四种调度机制代表了当前常见的先进并行调度机制，具体介绍参见文献[13]。本文选择Dynamic调度机制作为示例。

2.2 天梯地月转移轨道窗口计算并行设计

天梯系统的基本组成如图3所示，主要包括天梯绳索、地球表面节点、GEO节点、顶点锚、绳索攀爬器、地球表面运输系统和运营中心[14]。

图3 天梯系统组成示意图[15]Fig.3 Composition of space elevator system[15]

天梯绳索是天梯最重要的组成部分，其主要功能为向攀爬器提供依附的途径，使攀爬器能够沿着缆绳从地表节点进入空间，同时其还要平衡整个天梯的重力与系统绕地球转动形成的离心力；攀爬器为运输有效载荷进入空间的运载器，其沿着绳索爬升，进入轨道预定位置后将有效载荷释放；地球表面节点和顶点锚分别位于绳索的两端，起到固定绳索位置、调整绳索姿态的功能。整个天梯的质心设置在GEO节点位置，这样整个天梯系统就以地球的自转速度围绕地球旋转，从而保证天梯与地面相对静止[14,16]。

由于天梯从地表一直延伸到GEO更远端，在执行行星际发射任务时，在天梯不同的高度释放可以获得不同的能量。比如，在天梯远端顶点锚处(距离地心100 000 km)释放甚至无须施加速度增量就可以飞往火星[16]。本文设计的从天梯飞往月球的转移轨道算法，重点解决在天梯哪一高度释放才能以最小的代价飞往月球。

本文假定天梯初始位于升交点赤经60°赤道上空。转移轨道约束地月转移轨道真近点角差θPA<π，近月点轨道高度为50 km≤rH≤1 000 km。考虑到2025年3月白道面与赤道面相对夹角达到最大值，约为28.72°，本文窗口计算的时间段取为2025年3月。

本文采用基于数据分解的并行方式，主要设计两级并行算法：转移三角形形状并行计算问题和转移三角形的空间定向并行计算问题。具体流程如图4所示。

图4 轨道设计流程Fig.4 Flow chart of trajectory design

第一个问题是转移三角形形状计算问题并行化：在初估转移轨道特性时，rEA根据式(9)均匀选择若干个点作为并行化设计参数，从近地点出发飞行到入口点的飞行时间tPA取30～170 h，基于Brent算法求解转移三角形的真近点角，求得的结果存储下来用于下一个子问题的搜索。

第二个问题是转移三角形的空间定向问题并行化：天梯地月转移轨道窗口计算时，以到达入口点时刻tA作为划分并行颗粒度的设计变量，计算1个月的时间周期。以到达入口点时刻作为并行颗粒度划分的主要好处是可以在并行计算之前计算好tA时刻的月球星历。在计算空间定向时，轨道倾角i∈[-0.5°,0.5°]。在前一问题中求得的满足约束的转移三角形数据库中，求解满足式(13)的Brent子问题，从而求解出对应的转移轨道空间定向参数轨道倾角。然后判断所求得的轨道是否满足地月转移轨道条件，如果满足则找到一条可行的转移轨道。

2.3 天梯奔月窗口计算结果

下面分别计算GEO点释放和天梯远端顶点锚处释放奔月的计算结果，分别如图5和图6所示。本文的算例中，采用一台Windows 10系统的电脑(AMD 3700X八核十六线程CPU，主频3.6 GHz，内存8G)，rEA取500个点，tPA间隔取0.2 h，tA间隔取10 min，并行计算在天梯GEO点释放时1个月的奔月窗口需要437.57 s，串行计算需要3 040.32 s，并行加速比为6.95。

由图5和图6的计算结果表明，从天梯奔月每月内存在两次窗口，每次窗口持续4～6天。对于奔月任务，天梯顶点锚处释放所需的速度增量反而比在GEO节点直接奔月所需的速度增量大，这主要是由于在远端顶点锚处释放的地月转移轨道获得了过多的能量，此能量甚至能飞行到火星，但不适合用于月球轨道转移。为了详细计算窗口，还需要把rEA、tPA和tA的间隔取得更密集一些，但这里用于了解转移轨道的特性已经足够。

(a) 飞行时间结果(a) Results of flight time

(a) 飞行时间结果(a) Results of flight time

为寻找到底在何处释放可以以较小代价飞往月球，计算了天梯不同轨道高度释放的奔月窗口，计算结果表明：在天梯距地心51 000 km处释放进入地月转移轨道，所需要的速度增量较小，所需速度增量如图7所示。在此处释放飞行器获得的相对地心惯性系的线速度为3.719 km/s。

(a) 飞行时间结果(a) Results of flight time

为详细研究从地心距51 000 km处释放的地月转移轨道特性，rEA取2 000个点，tPA间隔取0.1 h，tA间隔取1 min，并行计算天梯在GEO点释放时1个月的奔月窗口需要30 220.12 s(合503.7 min)。

如图8所示，在距地心51 000 km处的天梯奔月环月轨道倾角分布在10°～170°之间。

图8 月球轨道倾角与升交点赤经Fig.8 Inclination and RAAN of Moon orbit

天梯地月转移轨道的月球影响球入口点如图9所示，在月球影响球上西半球，在南、北纬度均有分布。

图9 入口点经纬度分布Fig.9 Latitude and longitude of entry point

以寻找到的速度增量最小的转移轨道为例，输入STK进行验证，计算得到的转移轨道根数如表1所示，到入口点飞行时间111.9 h，入口点对应历书时儒略日(对应STK的JED时间)为2 460 747.973 611 11，求得的最小速度增量为0.855 m/s，近月点高度为517.040 km。

表1 地月转移轨道入口点根数

基于商业软件STK的Astrogator模块进行验证，STK/Astrogator在地球段和月球段轨道预报器分别选地球点质量和月球点质量模型，STK计算得到的近月点高度为517.645 km。本文计算结果与之接近，显示了本文算法的正确性。设计结果如图10所示。

图10 天梯地月转移轨道Fig.9 Earth-Moon transfer orbit from space elevator

3 结论

本文提出一种基于飞行轨道面参数描述地月转移轨道的双二体模型表达方式，避免采用传统的基于月球影响球入口点经纬度的描述方式，该表达方式由轨道定义出发，通过地月几何关系来表述，更加明确直观。通过表述方式的转换把原来的三维球面搜索算法降维成为二维平面内圆上的搜索算法，结合一维非线性方程求根算法Brent算法和Lambert原理，可以高效地求解地月转移轨道的形状参数。

通过合理的解耦分解，将原始的轨道窗口多变量搜索问题进一步分解为两个子问题：一个为转移三角形形状计算问题，通过转移轨道形成的三角形几何关系，结合Lambert原理求解出转移轨道的形状参数(半长轴、偏心率及真近点角)；另一个为转移三角形的空间定向问题，基于已求得的转移轨道形状数据匹配搜索可行的转移轨道，确定剩余的三个轨道面相关参数。最后为了加速窗口搜索过程，充分发挥多核计算机算力，形成一种转移三角形形状计算问题和空间定向问题的两级并行算法。

基于本文的并行圆锥曲线几何切面法，计算了天梯不同高度进行奔月任务的轨道窗口，结果表明：

1)在天梯远端释放执行奔月任务效果甚至不如在GEO点直接释放的效果。

2)在距地心51 000 km左右释放执行奔月任务所需的速度增量极小。

3)天梯出发的奔月环月轨道轨道倾角分布在10°～170°之间。入口点在月球影响球上西半球，在南、北纬度均有分布。

4)计算天梯奔月1个月的发射窗口，本文的两级并行算法加速比达6.95。