航天器网络基于四元数表征的全局姿态同步

孟德元,伞扬,张凡

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

自20世纪90年代以来，随着小卫星技术的发展，以小卫星编队为代表的航天器网络逐渐成为姿态控制问题的研究热点.航天器网络通常由空间上呈现一定构型的多个航天器构成[1].为实现特定的合作目标，航天器网络的姿态协同至关重要，其中姿态同步是姿态协同中的重要研究部分[2].如深空探测中，航天器网络中的遥测设备等有效载荷需指向同一方向，才能实现完整的信息采集；交会对接时，主从航天器的姿态同步是安全对接的必要条件[3].因此，探索如何实现航天器网络的姿态同步具有重要的实际意义和研究价值.

对于航天器网络的全局姿态同步，如何合理表征各航天器的姿态是关键问题之一.常用的姿态表征方法主要有旋转矩阵、欧拉角和四元数.文献[4-5]使用旋转矩阵法表征姿态信息，但这种方法参数量大，计算复杂，且9个参数内含冗余信息.文献[6]中提出在大角度机动中，欧拉角法可能会因为旋转角度特殊而出现奇点.与以上两种方法相比，四元数法表征参数少，不存在奇点问题，因而在全局姿态表征方面具有天然优势.然而，四元数在表征姿态中存在着非唯一映射的问题，即同一个物理姿态可以映射为一对共轭四元数，导致全局姿态同步协议设计和分析上的困难[7].

另一个关键问题是如何设计姿态协议实现全局姿态同步.由于四元数处于非欧氏空间，且利用四个参数表征三维空间的指向信息，若同步协议设计不当可能出现“非同步陷阱”，即仅矢量部分收敛，而标量部分不收敛，从而姿态并未实现同步.文献[8-9]针对航天器网络，构造基于四元数矢量的控制协议，仅能实现矢量部分的收敛，但未考虑四元数标量的收敛.文献[10]利用四元数的矢量和标量相除设计控制协议，虽然成功地将拓扑结构放宽到非结构平衡的强连通图，但对于初始姿态仅能得到几乎全局同步.因此，构造全局姿态同步协议仍具有挑战性.

受上述已有工作的启发，本文提出了两类基于四元数表征的姿态同步协议，实现强连通航天器网络的全局姿态同步.第一类协议仅使用四元数的矢量部分，对四元数标量初值进行非负处理，然后分别对标量部分和矢量部分的演化进行分析，得到数学意义下的姿态同步结果.第二类协议进一步引入实时四元数标量符号，避免对标量部分的单独分析，最终得到更一般性的物理意义下的姿态同步结论.最后通过仿真分析，验证了两类协议在任意初始物理姿态下的姿态同步效果.

1 预备知识

1.1 网络拓扑

网络拓扑是研究航天器网络的基础，描述了各航天器之间的通信连接方式.网络拓扑可以利用有向图G={N,E,A}进行描述，其中N={1,2,…,n}表示n个航天器的集合，E⊆N×N表示代表通信与感知的边的集合，A=[aij]∈Rn×n表示G的邻接矩阵.有向边(j,i)∈E表示航天器j是航天器i的邻居，此时aij=1(i≠j)，否则，aij=0.航天器i的所有邻居节点构成的集合定义为Ni={j:j∈N且(j,i)∈E}.如果从航天器i到航天器j之间存在有向边的序列，那么这个序列称为有向路径.如果任意一个航天器均存在到达其他航天器的有向路径，则称有向图G是强连通.相应的拉普拉斯矩阵定义为L=[lij]∈Rn×n，其中对于i≠j，lij=-aij，否则，对于i=j,lii=∑j∈Niaij.

1.2 姿态表征

四元数(ε,q)∈R×R3是一种基于欧拉旋转定理的姿态表征方式.欧拉旋转定理是指刚体绕定点的任意有限转动可由绕过该点的某根轴的一次转动实现.具体来说，四元数的具体定义如下[11]：

(1)

其中单位矢量e∈R3表示欧拉轴，φ∈R表示绕e旋转的欧拉角.根据(1)式，可得单位约束如下:

ε2+qTq=1.

(2)

注1根据(1)和(2)式，可知(ε,q)和(-ε,-q)表示相同的物理姿态，因此相同的四元数表示相同的物理姿态，而相同的物理姿态可以表示为不同的四元数.根据如上表述，在下一节中对同步问题进行分类考虑.

2 问题描述

考虑由n个航天器组成的航天器网络，根据四元数定义，可以得到第i个航天器的姿态运动学为[11]：

(3)

其中，εi(t)和qi(t)分别为本体系相对于惯性系的四元数标量和矢量，ωi(t)为本体系相对于惯性系的旋转角速度在本体系上的投影，×表示矢量叉乘运算.

根据姿态运动学(3)式，本文的目标为设计关于ωi(t)的姿态同步协议，对于任意初始物理姿态，实现基于强连通拓扑的航天器网络的姿态同步.具体来讲，分为如下两个目标：

(a)数学意义下的姿态同步：当时间趋于无穷时，强连通网络下所有航天器的四元数(εi,qi)最终达到一致，即对于任意i∈N和j∈N，

(4)

(5)

(b)物理意义下的姿态同步：当时间趋于无穷时，强连通网络下所有航天器的物理姿态最终达到同步，即对于i∈N和j∈N，

(6)

其中，对于任意x∈R，符号函数定义为：如果x≥0，则sgn(x)=1，否则sgn(x)=-1.

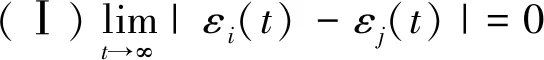
注3需要注意的是，尽管四元数遵循单位约束(2)，但是目标(a)中仅根据(5)式，并不能得到(4)式，因此(4)和(5)式必须同时成立，否则可能导致所谓的“非同步陷阱”，即仅矢量部分收敛，而标量部分不收敛.

3 主要结果

本节分别给出基于初始四元数标量符号的控制协议和基于实时四元数标量符号的控制协议，并分别证明了在相应控制协议下航天器网络最终能够达到姿态同步.

3.1 基于初始四元数标量符号的协议设计

首先，给出基于初始四元数标量符号的同步协议：

(7)

在此控制协议的基础上，对四元数标量进行分析，进而推导出航天器网络的全局姿态同步结果.

3.1.1四元数标量分析

在对航天器四元数进行分析时，根据单位限制(2)可知，四元数会出现非唯一映射问题.为解决这一问题，本节给出一个强连通拓扑下有关四元数映射唯一性的引理.该引理说明了四元数映射的唯一性与标量初值之间的关系.

引理1针对由n个航天器组成的强连通网络(3)，采用同步协议(7)，如果所有航天器四元数标量均满足εi(0)≥0，则对于t>0，有εi(t)≥0，∀i∈N.

证明假定k(t)为t时航天器网络中标量最小的航天器编号，即

(8)

则有εk(t)(t)≤εj(t),∀j∈Nk(t).进而，可知εk(t)(t)为连续分段可导函数.根据(2)和(8)式可得

(9)

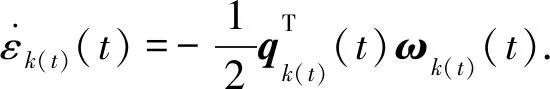
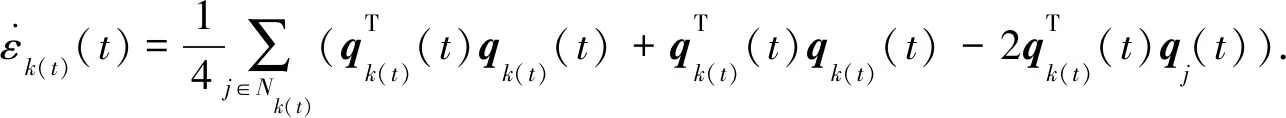
注4根据引理1，如果所有航天器均符合εi(0)≥0，则同步协议(7)可以保证所有的四元数标量始终保持非负.考虑单位限制(2)，若已知四元数的矢量，则可以唯一确定对应的标量数值，这样即可避免“非同步陷阱”.另外，根据四元数定义(1)，εi(0)≥0可以映射所有物理姿态，即可进行全局姿态表征.

3.1.2数学意义下的姿态同步分析

本节对强连通拓扑下航天器网络的姿态同步进行分析，首先给出关于强连通拓扑的一个引理.

引理2[13]针对由n个航天器组成的强连通网络(3)，存在p=[pi]∈Rn，其中pi>0，∀i∈N，使得

(10)

引理1和引理2给出了在强连通拓扑下网络中航天器四元数标量和矢量的性质.要证明航天器网络的全局姿态同步，还需对整个时域上航天器四元数的一致性进行分析.进一步，给出基于初始四元数标量符号的协议设计的定理：

定理1针对由n个航天器组成的强连通网络(3)，对于任意初始物理姿态，如果εi(0)≥0，且采用同步协议(7)，所有航天器的四元数表征最终趋于一致，实现全局同步，即(4)和(5)式成立.

证明考虑以下能量函数：

(11)

对(11)式中的能量函数求导，并考虑姿态运动学(3)和协议(7)，可得

(12)

将(10)式代入(12)式，可得

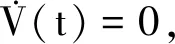
注5定理1中的条件εi(0)≥0，∀i∈N是合理的.根据(1)式，可知当εi(0)≥0，相应的欧拉角φi(0)范围为[-π,π]，即符合此初值的四元数集合可以映射所有物理姿态空间.另外需要说明的是，如果四元数初值(εi(0),qi(0))中εi(0)<0，根据注1可以将四元数初值预处理为(-εi(0),-qi(0)).

注6相比于文献[8]，本文提出的基于初始四元数标量符号的协议设计，可以保证四元数的标量部分和矢量部分分别收敛，从而保证姿态同步，避免了文献[8]中的“非同步陷阱”.

3.2 基于实时四元数标量符号的协议设计

在定理1的基础上，进一步将四元数标量的符号引入控制协议，就可以避免对四元数初始值标量符号的判断和处理，只需根据控制协议直接对航天器网络进行同步分析.同样地，首先给出同步协议为：

(13)

基于此协议(13)，给出如下姿态同步定理.

定理2针对由n个航天器组成的强连通网络(3)，给定任意初始四元数，若采用分布式同步协议(13)，则所有航天器的物理姿态最终趋于同步，即(6)式成立.

证明采用定理1中的能量函数(11)，对其求导并代入姿态运动学(3)和姿态协议(13)，可得

(14)

根据引理2，对(14)式进行进一步化简：

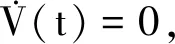
注7相比于定理1，定理2在姿态同步协议(13)中引入了符号函数，这种方式的优势在于，在分析收敛性时不必考虑航天器四元数标量的符号.尽管当时间趋于无穷时，各个航天器的四元数未必趋于相同，但是保证了物理意义下的姿态同步目标的实现，符合实际应用需求.

4 数值仿真

在本节中，对所提两类姿态同步协议(7)和(13)的有效性进行验证，利用刚体航天器网络进行数值仿真，仿真步长为0.1 s，仿真时长为20 s.邻接矩阵A的非零项设置为a12=1,a15=1,a23=1,a24=1,a34=1,a41=1,a54=1.四元数初值矢量部分分别为：

q1(0)=[0.293 4,-0.155 6,0.769 5]T,q2(0)=[-0.248 0,0.305 9,-0.876 1]T,

q3(0)=[-0.255 8,-0.730 6,0.556 5]T,q4(0)=[0.763 1,-0.306 8,0.381 5]T,

q5(0)=[-0.521 1,0.077 5,0.841 6]T.

为验证仿真协议(7)，取标量的初值为：

ε1(0)=0.684 6,ε2(0)=0.219 4,ε3(0)=0.279 8,ε4(0)=0.410 3,ε5(0)=0.093 9.

为验证仿真协议(13)，取标量的初值为：

ε1(0)=-0.684 6,ε2(0)=0.219 4,ε3(0)=-0.279 8,ε4(0)=0.410 3,ε5(0)=-0.093 9.

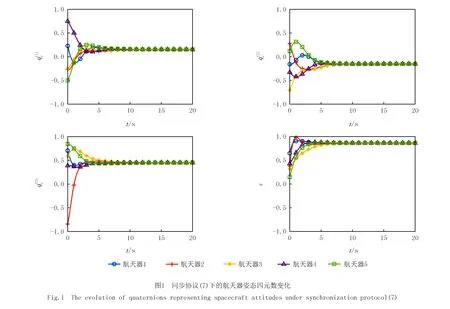
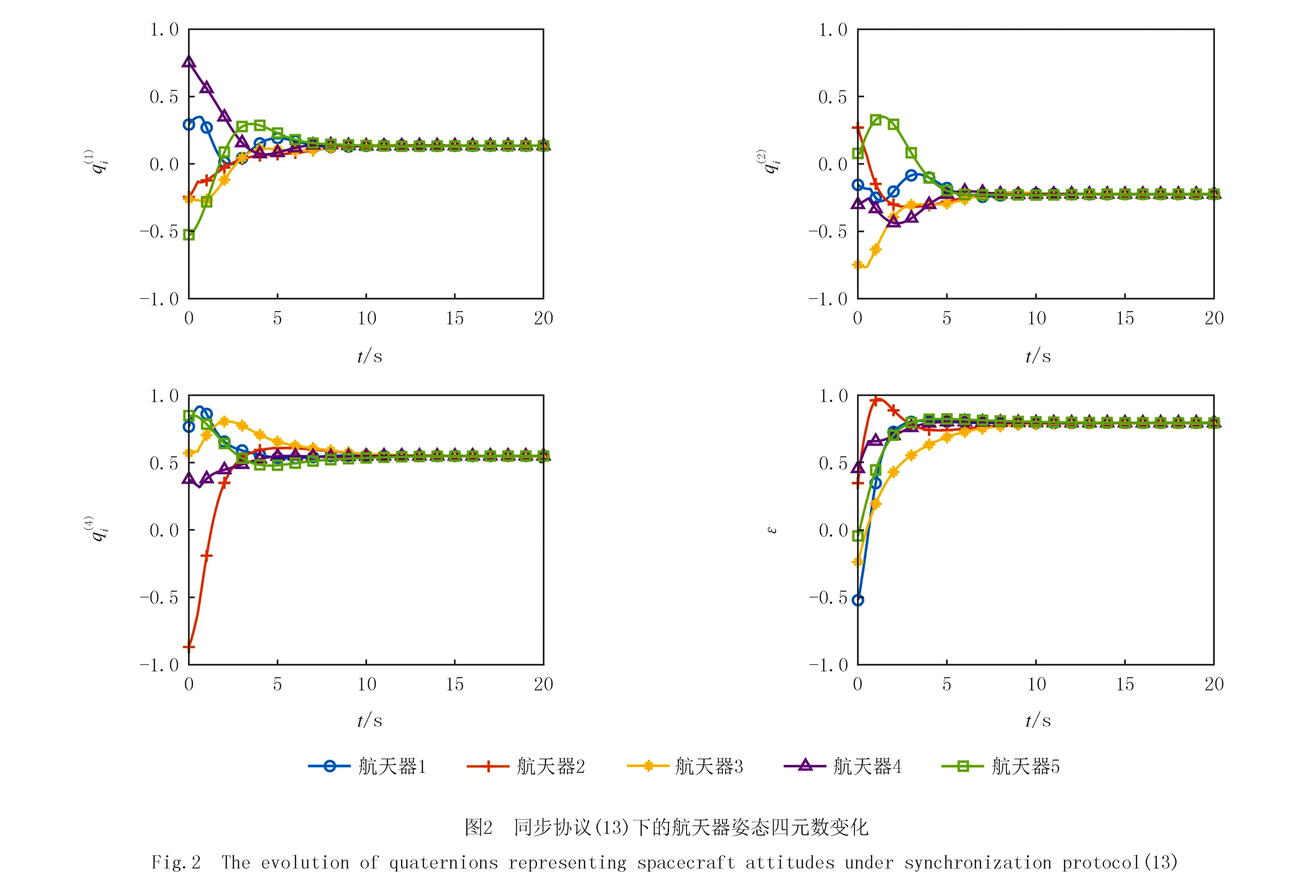
对标量和矢量分别作图，以判断其收敛性.结果如图1和图2所示.

从图1中可以看出，四元数矢量和标量分别收敛，此时航天器之间达成姿态一致.另外，通过标量的变化曲线可以看出，在初始值非负时，标量在整个时域内保持非负.因此，根据定理1的结论和图1的仿真结果可知，对于任意初始物理姿态的航天器网络，使用本文提出的控制协议(7)能够使系统实现全局姿态同步.

从图2中四元数标量部分的变化曲线可以看出，在对控制协议引入符号函数之后，即使存在标量初值为负的航天器四元数，在整个时域上各个航天器的四元数仍能趋于一致.因此，根据定理2的结论和图2的仿真结果可知，对于任意初始物理姿态的航天器网络，使用本文提出的控制协议(13)也能够使系统实现全局姿态同步.需要说明的是，定理2可以实现物理意义下的姿态同步，但并不能保证四元数一定实现同步.

5 结 论

本文针对拓扑结构为强连通的航天器网络的全局姿态同步问题，设计了两类基于四元数的同步协议.第一类协议仅使用四元数矢量部分.首先，基于四元数非唯一映射，通过预处理保证初始四元数标量非负，进而证明在第一类协议下，标量部分始终非负.然后，通过构造能量函数证明趋于一致.根据单位约束，可以证明标量部分也收敛到相同的数值，即数学意义下的姿态同步.第二类协议在第一类协议的基础上，引入实时四元数标量符号，无需对标量部分的演化单独分析，可以得到更一般性的物理意义下的姿态同步.通过对给定的强连通航天器网络的仿真分析，验证了两类协议的全局姿态同步效果.