高中解析几何试题背景知识研究
北京市朝阳区北京中学(100018)孙鹏
1 定值子弦
定义:设过点P是某圆锥曲线的一个顶点,PA,PB是该曲线过顶点P的两条弦,当直线PA,PB的斜率之积为定值λ时,称线段AB为该曲线顶点P的关于定值λ的斜率等积子弦;当直线PA,PB的斜率之和为定值λ时,称线段AB为该曲线顶点P的关于定值λ的斜率等和子弦,这两个子弦统称为顶点P关于定值λ的定值子弦.
题目一(2022 年北京丰台区高三期末第20 题)已知椭圆C:=1(a>b>0)过点离心率为
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C的右顶点为A,过点D(4,0)的直线l与椭圆C交于不同的两点M,N(均异于点A),直线AM,AN分别与直线x=4 交于点P,Q.求证:|DP|·|DQ|为定值.
1.1 试题分析


1.2 试题几何本质探究

说明结论1 中当顶点为左顶点时亦成立,证明过程一致.
结论2椭圆C:=1(a>b>0)的右顶点为A,点D(x0,0)为x轴上一动点,过点D的直线l与椭圆C交于不同的两点M,N(均异于点A),则直线AM与AN斜率之积为常数.
证明设点M(x1,y1),N(x2,y2),直线l方程为y=k(x-x0),则


图1
结论3椭圆C:=1(a>b>0)的右顶点为A,点D(x0,0)为x轴上一动点,过点D的直线l与椭圆C交于不同的两点M,N(均异于点A),直线AM,AN分别与直线x=x0交于点P,Q,则|DP|·|DQ|为定值(如图1).

2 椭圆的共轭直径

(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆C上一动点(不在x轴上),M为AP中点,过原点O作AP的平行线,与直线x=3 交于点Q.问:直线OM与FQ斜率的乘积是否为定值? 若为定值,求出该值;若不为定值,请说明理由.
2.1 试题分析

2.2 试题几何本质探究

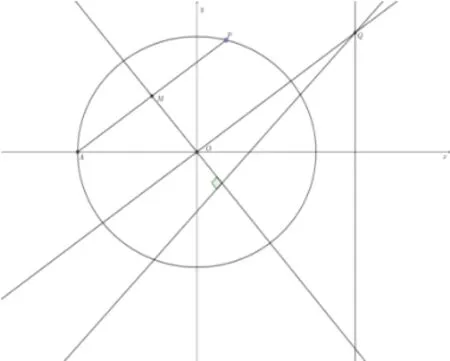
图2
结论4椭圆C:=1(a>b>0)左顶点为A,P为椭圆C上一动点(不在x轴上),M为AP中点,过原点O作AP的平行线,与直线x=x0交于点Q,过点Q与直线OM垂直的直线经过x轴上一定点(如图2).


