一维轴对称杆件爆源模型及其在台阶爆破模拟中的应用*

朱心广，冯 春，王心泉，程鹏达，高圣元

（1. 中国科学院力学研究所，北京 100190；2. 中国科学院大学工程科学学院，北京 100049；3. 煤炭科学研究总院，北京 100013）

台阶爆破技术作为一种高效经济的破岩手段，广泛应用于交通、矿山、水利水电等各个领域[1]。随着计算机技术的飞速发展，数值分析在台阶爆破技术中参数的选择及优化方面扮演着越来越重要的角色。目前关于爆炸问题的数值计算方法，按照有无网格可分为两类。网格类计算方法包括有限元法[2-5]和离散元法[6-8]，其中有限元法的数学模型和算法相对成熟，针对连续问题的分析以及应力场的描述方面具有优势，但是在大位移、大变形问题中常因单元过分畸变导致计算发散；离散元法在描述块体的大位移、碰撞、飞散等过程中具有优势，但是无法描述连续损伤过程。在网格类的计算方法中，为了获得精确结果，需要在爆源附近加密网格，导致网格数量增大，增加了计算时间。无网格的计算方法包括物质点法[9-10]（material point method, MPM）、光滑粒子流体动力学[11-14]（smoothed particle hydrodynamics, SPH）等，其突出特点是在计算过程中与网格无关，因此不存在网格加密的问题，但是和有限元相比数学模型和算法还不够成熟，计算精度和计算效率还有一定差距。

对于爆破问题的数值模拟，比较成熟的商业软件包括LS-Dyna、Autodyn、UDEC 和3DEC 等，常用的计算方法包括非连续变形分析法（discontinuous deformation analysis, DDA）、有限离散元（finite discrete element method, FDEM）以及连续-非连续单元法（continuous-discontinuous element method, CDEM）等。余仁兵等[15]通过LS-Dyna 软件对不同直径炮孔不耦合装药结构简化模型进行了数值模拟；丁希平[16]采用LS-Dyna 软件研究了炸药单耗、超深及填塞长度对爆破效果的影响；璩世杰等[17]运用LS-Dyna 软件研究了不同角度的节理对预裂爆破效果的影响。刘超[18]使用Autodyn 软件针对两种不同的间隔装药方式建立计算模型，计算结果表明中间隔位置错开的装药结构相对中间隔位置对齐的装药结构而言，各处压力大小分布更加均匀，有效作用时间更长；谢冰等[19]运用Autodyn 与UDEC 相结合的方法，研究了节理几何特征对预裂爆破的影响。Yan 等[20]利用3DEC 软件，通过在炮孔破碎圈外侧施加等效破碎载荷，并控制不同区域的网格尺寸，研究了三维条件下爆堆的形成过程。郭双等[21]基于DDA 方法建立了岩石爆破力学模拟模型，分别研究了地应力对爆生气体压力和爆炸应力波破岩效果的影响；江成等[22]采用DDA 方法模拟了爆炸应力波作用下考虑地应力条件时的单孔和多孔凿岩爆破破岩过程。Han 等[23]采用FDEM 方法并运用GPU 并行加速的方式，研究了爆破作用下，对某含有台阶段深埋隧道的损伤演化过程。郑炳旭等[24]基于CDEM 方法，探讨了炸药单耗对爆破块度分布曲线及系统破裂度的影响规律；冯春等[25]通过在CDEM 方法中引入朗道爆源模型、弹性-损伤-断裂本构及半弹簧接触算法[26]，模拟了从炸药起爆、岩体损伤破裂到最后爆堆形成的全过程。

在爆源模型的处理上，ABAQUS 和LS-Dyna 通常建立炸药与空气数值分析模型并借助其状态方程施加爆炸荷载，该方法需要对炸药和空气分别单独划分网格并赋予其各自的状态方程，且炸药网格和空气网格应在交界面上共节点，操作较为复杂且需要较长的计算时间。一般而言，钻孔爆破的炮孔尺寸在厘米至分米量级，而待爆岩体的范围则在米至数十米范围。数值模拟时，若将炮孔与待爆岩体均用实体网格进行剖分，将会导致炮孔附近的网格过密，从而使得整个模型的网格数量过大而影响计算效率。为解决上述问题，本文基于CDEM[27]方法，提出一种利用线状杆件表述炮孔及炸药，通过线状杆件与周围实体单元的耦合实现爆破破岩过程模拟的计算方法。

1 杆件爆源模型

1.1 基本假设

(1) 炸药爆轰过程中满足轴对称假设，爆炸过程中炸药杆件单元在轴向上不发生膨胀，仅在径向发生膨胀。

(2) 炸药与实体单元满足压力-体积耦合关系，即炸药单元传递给实体单元膨胀应力，实体单元传递给炸药膨胀体积。

(3) 不考虑爆生介质与炮孔壁对的相互作用，直接将爆轰产物产生的气体压力作用于周边围岩，以加快求解速度。

由于不考虑爆轰产物与炮孔的相互作用过程，因此该模型对炸药近场的模拟不是很准确。如图1 所示，Ei表示待爆岩体网格，Ni表示杆件单元节点（i=1,2,3,···）。实施本文所述的方法时，首先将待爆岩体采用较大的实体网格进行剖分，然后将炮孔简化为杆件插入至待爆岩体的指定位置；杆件上划分若干单元，单元中引入经典的朗道爆源模型；判断每个杆件节点与实体单元的拓扑关系，若该杆件节点位于某个实体单元的内部或表面，则将该实体单元作为杆件节点的传力对象，将杆件节点上的爆生气体压力施加至该岩石单元上；同时，根据该实体单元的体应变计算出杆件节点处的横截面变化情况，用于计算下一时刻的爆生气体压力。

图1 杆件单元与实体网格的耦合示意Fig. 1 Schematic of coupling of bar and solid mesh

1.2 朗道爆源模型

朗道模型采用朗道-斯坦纽科维奇公式（γ 率方程）进行爆炸气体膨胀压力的计算：

式中：γ1及γ2分别为第一段及第二段的绝热指数，对于一般的凝聚态炸药，γ1= 3，γ2= 4/3；p和V分别为高压气球的瞬态压力和体积，p0和V0分别为高压气球初始时刻的压力和药包的体积，pc和Vc分别为高压气球在两段绝热过程边界上的压力和体积。pc和p0分别为：

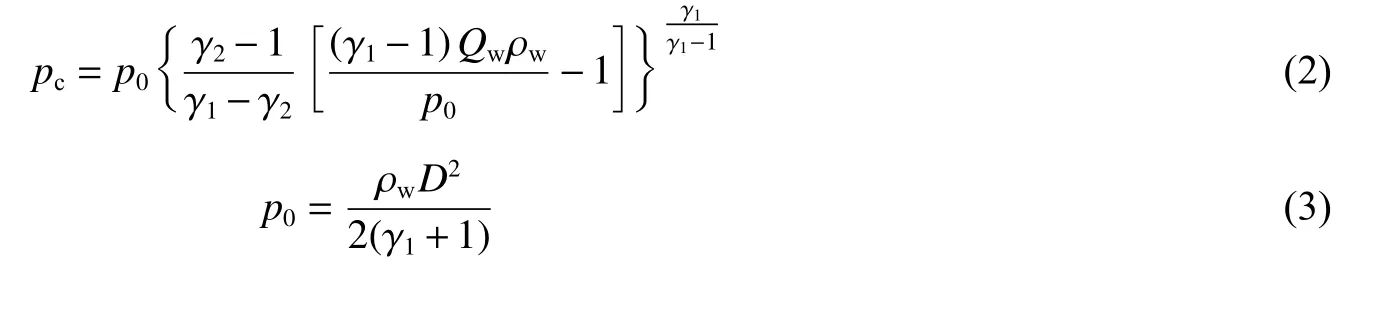
式中：Qw为炸药爆热，J/kg；ρw为装药密度，kg/m3；D为爆轰速度，m/s。

此外，当某时刻爆炸产生的压力大于CJ (Chapman-Jouguet) 面上的压力 (pCJ) 时，将该压力修正为CJ 面上的压力。

本文采用线状杆件描述炸药，每个炸药单元的初始体积及当前体积为

式中：r0为炸药单元的初始半径，h为炸药单元的长度，θe为炸药单元的平均体应变 (可通过与该单元存在耦合关系的岩石单元的体应变获得)。

为了模拟点火爆炸及爆轰波的传播过程，朗道模型中需设置点火点位置、点火时间，并根据到时起爆判断某一炸药单元是否执行爆炸压力计算。

设某一炸药 (含若干个杆件单元) 的点火时间为t0，点火点坐标为(x0,y0,z0)，该炸药中某一杆件单元的中心到点火点的距离为d，炸药的爆速为D，则该单元的点火时间为t1=d/D+t0。当爆炸时间t＞t1时，该单元开始进行爆炸压力的计算，计算公式为

式中：pr为真实爆炸压力，f(p)为爆轰产物状态方程 (可根据式(1)获得); ζ 为能量释放率：

钻孔爆破过程中，随着炮孔的起爆，爆生气体逐渐膨胀，并推动岩体做功。岩体在爆炸压力的作用下逐渐出现裂缝的萌生、扩展，并最终出现贯通裂缝。一旦出现贯通性的裂缝，炮孔内的气体将会从裂缝中快速溢出，并导致炮孔内的压力急剧下降。由于直接模拟爆生气体在岩体内的流动及溢出过程较为复杂，本文采用设置失效时间的方式进行等效模拟。当爆破时间大于失效时间时，该炮孔即设置为失效单元，失效单元中的气体压力pr为0，且不再进行爆炸压力的计算。

1.3 杆件单元与岩石单元的耦合

设某线状炸药中共有N个节点位于某个实体单元内部或表面 (图1)，则该线状炸药位于实体单元内部的平均爆压可表述为

式中：负号是因为爆炸压力以压为正，而应力以拉为正；σb为施加于实体单元上的膨胀应力，即可认为是施加在实体单元上的三项正应力（剪应力为0）；α为压力衰减指数（需根据数值实验进行标定）；d为实体单元的特征尺寸：

式中：Ae为二维实体单元的面积，Ve为三维实体单元的体积。

将上述膨胀应力转化为节点力施加于单元的各个节点上，为

式中：fni为单元中节点n第i个方向的节点力分量，M为单元中与节点n相关的面的数量，eki为与第k个面的单位外法向量在第i个方向的分量，Ak为第k个面的面积，Qk为第k个面的节点总数。

式(4)中炸药单元的平均体应变θe可表示为

式中：p、q为炸药单元的两个节点，θp及θq为与节点p、q 存在耦合关系的实体单元的体应变。

因此，虽然假定了炸药单元仅在径向发生膨胀，但是通过膨胀压力以正应力形式施加于实体单元节点，也可以实现实体单元的轴向膨胀破坏。

2 压力衰减指数α 的标定

在半无限岩体内设置一个直径为250 mm 的钻孔，钻孔深度为15 m，钻孔内的装药长度为8 m，填塞7 m。分别建立实体单元数值模型(模型A)及杆件-实体单元混合数值模型(模型B)，通过对比起爆后典型位置的径向幅值振动速度vp，来标定式(9)中压力衰减指数α 的具体数值。

由于在实体炮孔模型中，要求实体炮孔和围岩共节点，而杆件模型中不要求杆件与围岩单元共节点，从这一点来讲，无法做到两种数值模型完全一致。另外，本节的目的就是改变不同网格尺寸标定α 值，只需保证测点与爆心的距离相等即可，因此选择什么样的几何构型不是很重要。

如图2 所示，模型A 为1/4 圆柱模型，高为25 m，半径为25 m，炸药位于柱体中心轴线上。模型的外周面及底部设置为无反射边界条件，模型的对称面上施加法向位移约束条件。采用映射网格进行剖分，轴向共分割50 份 (每份0.5 m)，环向共分割15 份，炮孔部分的径向共分割3 份，岩体中的径向采用8、16、48 三种分割数进行分割，所建立的三种网格分别命名为网格A1 (每份3.11 m)、网格A2 (每份1.55 m)、网格A3 (每份0.518 m)。

模型B 的炸药采用杆件单元进行剖分，岩体采用六面体单元进行剖分 (如图3 所示)。岩体的高度25 m，长度及宽度均为50 m，岩体高度方向共分割25 份 (每份1 m)，水平方向分别采用16、25、32、50 四种分割数进行分割，所建立的4 种网格分别命名为网格B1 (每份3.125 m)、网格B2 (每份2 m)、网格B3 (每份1.5625 m)、网格B4 (每份1 m)。炸药单元位于模型正中，采用42 个杆件单元进行离散。为了消除人工边界的虚假反射，在模型四周及底面均施加无反射边界条件。

本节中岩体为赤铁矿，采用Mohr-Coulomb理想弹塑性模型(岩体单元间不考虑断裂)进行描述；炸药为现场混装乳化炸药，采用朗道爆源模型进行描述。岩体参数及炸药参数见表1 及表2。

表1 铁矿石的力学参数Table 1 Mechanical parameters of iron ore

表2 乳化炸药的参数Table 2 Parameters of emulsion

为了标定压力衰减指数 α ，选取模型A 及模型B 中的对应测点进行对比(测点位置见图2、图3)。该测点到爆源的径向距离为25 m，两个模型中测点的径向振动速度峰值随单元尺寸的变化如图4 所示。由图4 可得，随着单元尺寸的增大，两个模型所获得的测点处的径向速度幅值均线性减小；当压力衰减指数 α 为1.25 时，模型B 所获得的vp衰减规律与模型A 所获得的规律基本一致。由此表明，当式(8)中的压力衰减指数取1.25 时，一维轴对称爆源模型的爆破效果与实体模型的爆破效果基本一致。

图2 模型A (径向分割16 份)Fig. 2 Model A (dividing into 16 segment in the radial direction)

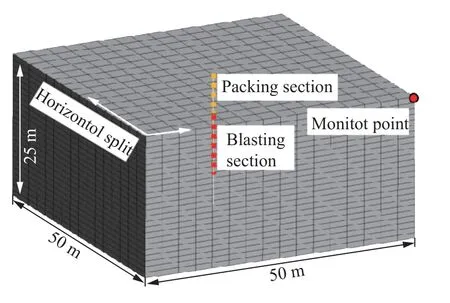
图3 模型B (水平向分割16 份)Fig. 3 Model B (dividing into 16 segment in the horizontal direction)

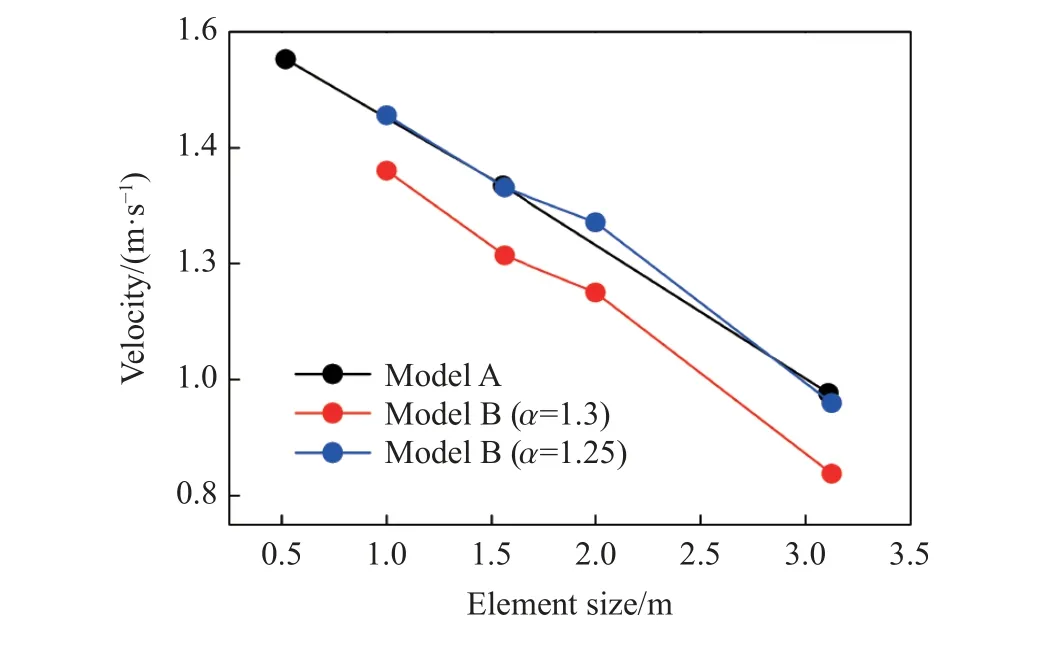
图4 测点处径向峰值振动速度随单元尺寸的变化Fig. 4 Variation of radial peak particle velocity at monitoring points with element size

网格A2 及网格B3 对应的径向网格尺寸均为1.5 m 左右，当模型B 中轴对称爆源模型所用的压力衰减指数 α 为1.25 时，两个网格获得的测点处的径向振动速度时程曲线如图5 所示。由图5 可得，两者的振动规律基本一致，仅起振时间及首峰后的振动规律有所差别，由此进一步证明了衰减指数 α 为1.25 时的一维轴对称爆源模型，其爆破效果可以与实体模型的效果基本一致。

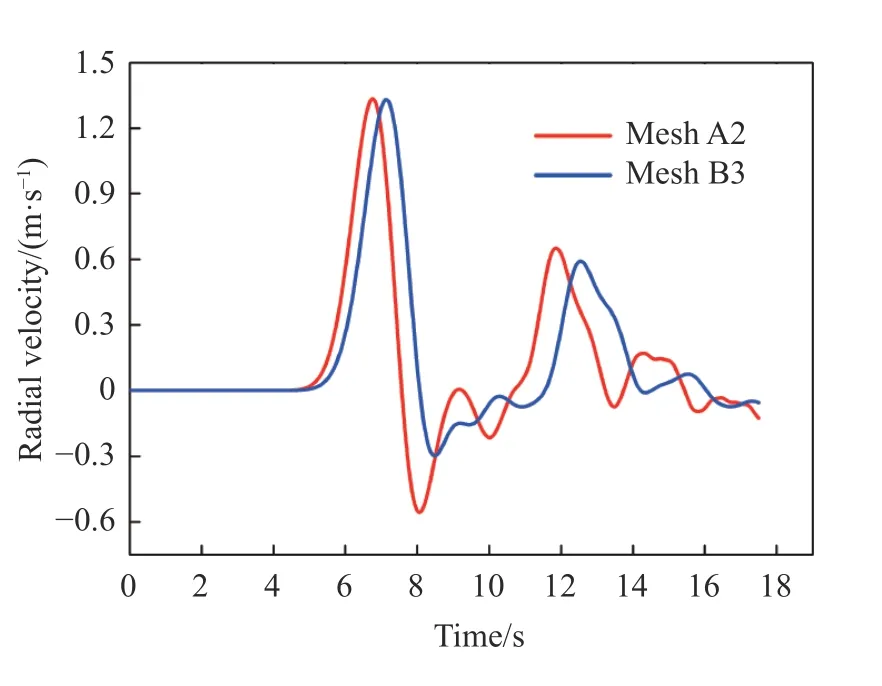
图5 测点处径向振动速度时程曲线Fig. 5 History of radial velocity at monitoring point

3 模型验证

建立如图6 所示的立方体混凝土模型，内部设置炮孔模型，混凝土尺寸为3.048 m×3.048 m×1.52 m，炮孔直径38 mm，长1200 mm，炮孔位置见剖面图。混凝土及炮孔力学参数采用文献[28]中数据，其中混凝土密度为2009 kg/m3，抗拉强度为1.8 MPa，弹性模量为13.1 GPa，泊松比为0.25；炮孔直径为38 mm，密度1150 kg/m3，爆速4700 m/s1，爆热3.24×106J/kg，杆件爆源中爆炸持续时间为15 ms。

当模型爆炸20 ms 时，位于炮孔中部位置的模型爆炸结果剖视图如图7 所示，其中最大位移发生在炮孔左侧的自由临空面处，最大位移值0.88 m，整个爆炸形态与文献[28]结果基本一致。

图7 位于炮孔中部位置的模型爆炸结果剖视图(20 ms)Fig. 7 Sectional view of model explosion results in the middle of the blast hole after 20 ms

4 工程应用

鞍钢露天铁矿台阶爆破现场图片如图8 所示。本文以鞍钢露天铁矿台阶爆破为例，根据爆破设计（图9(a)），建立如图9(b)所示的5 排10 列 (共50 个炮孔) 数值模型，该模型共包含19658 个计算网格，其中四面体单元数6541，三棱柱单元数720，金字塔单元数6916，六面体单元数6381. 根据现场情况，模型表面包含3 m 厚的松散堆积石土，下部为铁矿石块。炮孔深度为15 m，直径为0.25 m，超深3 m，段高12 m，间排距为7 m×7 m，单孔装药量677 kg，采用逐孔起爆方式，孔底起爆，孔间延时42 ms，排间延时65 ms，连线方式为串并联联结。

图8 鞍钢露天矿现场Fig. 8 Site view of Angang strip mine

图9 含50 炮孔的台阶爆破数值模型Fig. 9 The bench blasting model with 50 bore holes

松散堆积石土及铁矿石块采用Mohr-Coulomb 理想弹塑性模型进行描述，其中松散堆积石土的密度为1800 kg/m3，弹性模量为6 GPa，泊松比为0.25，内聚力15 MPa，抗拉强度5 MPa，内摩擦角40°；铁矿石块弹性模量为4 GPa，其他力学参数见表1。爆炸所用炸药采用现场混装的乳化炸药，其参数见表2。

数值计算共分为两个阶段：第一阶段采用虚拟质量法获得模型在重力作用下的静态应力场，该阶段中模型四周及底部为法向约束边界，重力方向竖直向下；第二阶段起爆阶段，模型底部及四周施加无反射边界，计算时步为0.3 µs，Rayleigh 阻尼中刚度阻尼系数为1×10-4，质量阻尼系数为0。

台阶爆破后露天边坡的破坏状态如图10 所示，由图可以直观看出，爆区内整体以拉伸破坏为主，只有在爆区顶部及台阶拐角处出现零星剪切破坏。

图10 台阶爆破后边坡的破坏状态Fig. 10 Failure status of slope after bench blasting

在地表布设5 个监测点，分别为M1～M5(图9(b))，其中M1 与M2 的间距为18.5 m，M2 与M3 的间距为17.2 m，M3 与M4 的间距为17.8 m，M4 与M5 的间距为18.5 m。获取各个测点处振动速度峰值并与现场实测数据对比，绘制曲线如图11 所示。由图11 可得，爆点与测点的水平距离越大，测点的振动峰值速度越小，数值计算结果与现场实测数据的误差越小，说明运用本文所提出的杆件爆源模型进行远场的爆炸模拟的结果是可信的，也证明了杆件爆源模型的有效性与合理性。

图11 峰值振动速度随距离的变化曲线Fig. 11 The curve of peak particle velocity with distance

5 结 论

(1) 提出了一种一维轴对称杆件爆源模型，利用线状杆件表述炮孔及炸药，炸药(杆件)单元传递给周围实体单元膨胀应力，实体单元传递给炸药膨胀体积，两者通过压力-体积耦合关系实现炸药与周围岩体的相互作用。

(2) 通过与实体炮孔模型的数值对比分析，当压力衰减指数 α =1.25 时，本文所提爆源模型获得的径向振动速度峰值衰减规律与实体炮孔模型所获得的规律基本一致，并且针对混凝土块破坏特性分析，其破坏形态与文献基本一致。

(3) 以鞍钢露天铁矿台阶爆破开采为背景，模拟了5 排10 列共50 个炮孔逐孔起爆后，爆区内的损伤破坏状态。数值计算结果表明，爆区内以拉伸破坏为主，并且所获得测点处的振动速度峰值随距离的变化规律与现场实测数据基本一致。

(4) 采用一维轴对称爆源模型后，炮孔附近不再需要加密网格，因此可以降低计算网格数量并增大计算步长，并最终实现炸药起爆过程及爆炸地震波传播过程的统一高效模拟。