负高斯曲率曲面薄壁管吸能特性研究*
马梓鸿,张慧乐,孙泽玉,陈慧敏,岳晓丽
(1. 东华大学机械工程学院,上海 201620;2. 东华大学上海市轻质结构复合材料重点实验室,上海, 201620;3. 电子科技大学长三角研究院(湖州),浙江 湖州 313000)
随着我国汽车产销量的逐年增长,交通安全问题已经成为我国汽车工业发展所面临的重要问题之一。薄壁吸能结构在受到冲击载荷作用时,能够吸收耗散碰撞动能,因此薄壁结构在耐撞性领域得到了广泛应用。
目前,薄壁结构表面形状以零高斯曲率曲面为主,但自然界中还存在负高斯和正高斯曲率曲面。数学家高斯将其总结为“高斯绝妙定理”[1]:对于任意曲面,当该曲面内任意点P的两条主曲线曲率k的乘积为负时,则该曲面为负高斯曲率曲面,同理可得零高斯及正高斯曲率曲面。负高斯曲率曲面在建筑领域受关注较多[2-3],但在薄壁结构耐撞性领域鲜有研究。
在针对薄壁结构耐撞性和吸能特性的研究中,研究者们较多关注横截面为方形[4-5]、六边形[6-7]、八边形[8-11]和圆形[12-13]的薄壁管。张宗华等[14]对上述4 类薄壁管进行动态轴向冲击模拟后发现从方形到六边形,结构压溃力和吸能量显著提高,但八边形后趋于稳定,圆形截面优势并不显著。Guillow 等[15]研究了不同长径比和径厚比下薄壁圆管的压溃响应,发现其变形模式主要包括轴对称变形、金刚石变形、混合变形(轴对称变形和金刚石变形共存)以及欧拉屈曲等4 类。为进一步探究薄壁圆管吸能特性,Zarei 等[16]、Hou 等[17]和Marzbanrad 等[18]基于响应面法和遗传算法对薄壁圆管进行了多目标优化设计,提高了吸能量的同时降低了结构质量。但上述研究对象表面形状按照高斯曲率类型分类仍属零高斯曲率曲面,对于负高斯曲率情况下的薄壁管吸能特性研究较少。
为设计出吸能特性优良的薄壁管,本文中将负高斯曲率曲面形态引入薄壁管设计中,提出一种新型负高斯曲率曲面薄壁圆管结构(negative Gaussian curvature surface circular tube,NGC-C)。利用经验证的有限元分析方法对其进行轴向动态冲击模拟,提取各项性能指标。借助复杂比例评估(complex proportion assessment,COPRAS)法将其与传统薄壁管进行性能比对。采用拉丁超立方采样法构建样本空间并获取各样本点对应的性能响应值,进一步推导出其代理模型。基于此代理模型,借助改进非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA-Ⅱ)进行多目标优化设计。以期为薄壁吸能结构的设计提供新思路。
1 有限元模型及验证
1.1 有限元模型建立
薄壁管设计参数主要有:口径R、厚度T、曲率参数G和长度L。固定长度L=180 mm,如图1(a)所示。当曲率参数G分别取负数、零、正数时,薄壁管形状分别呈负高斯曲率曲面、零高斯曲率曲面以及正高斯曲率曲面,传统薄壁结构一般为零高斯曲面。
利用非线性有限元软件LS-DYNA 进行动态轴向压溃数值模拟分析,并利用Ls-Prepost 4.8 软件进行前后处理。薄壁管单元类型为Belytschko-Tsay 壳单元,采用全积分方法,厚度方向积分点设置为5。为防止管件自身在变形过程中出现穿透现象,利用Automatic single surface 单面自动接触类型来设置管件自身接触,利用Automatic surface to surface 定义管件与冲击墙之间的接触[18],摩擦因数设置为0.25[16]。图1(b)展示了3 种网格尺寸(4、3 和2 mm)的载荷-位移曲线,当网格尺寸为3 mm 时,其载荷波动趋势与网格为2 mm 的吻合度较高,且初始峰值力、平均压溃力以及总吸能等指标相差均在3%以内;而网格尺寸为4 mm 时曲线整体偏低,尤其第2 个峰值力相较于2 mm 网格下降了16%。当网格进一步细化会大幅增加计算时间,3 mm 网格计算结果已经能够满足分析需求,因此采用3 mm 网格。设置薄壁管底部边缘为固定支撑。上端有300 kg 刚性冲击墙,以6.0 m/s 初速度冲击薄壁管,并设置其只存在轴向位移自由度。薄壁管材料选用A6060-T5 铝合金[12],使用LS-DYNA 中的MAT103 号材料模型,材料参数见表1。由此建立G=0 时的有限元模型(finite element model, FEM),如图1(c)所示。

图1 有限元模型以及网格选择Fig. 1 Finite element model and element size selection

表1 材料参数Table 1 Material parameters
1.2 有限元模型验证
如图2,有限元模型求解后得出的沙漏能(hourglass energy)对总能量(total energy)的占比小于5%,求解结果收敛性良好。为验证有限元模型的可靠性,借鉴文献[18]的验证方法,利用相关文献实验结果验证有限元模型可靠性。首先分别构建出文献[6]中讨论的方形、六边形、圆形和文献[11]中探究的八边形截面薄壁管,这4 个模型受动态轴向压溃后实验与数值模拟的变形模式结果对比情况可见图3,各模型实验与数值模拟的变形模式相似度较高。进一步地,构建出文献[16]中具有代表性的S-1、S-3、S-5 和S-6 薄壁圆管模型,其参数见表2。由于文献中只给出了S-1 模型的变形模式和力-位移曲线,因此将S-1 实验与数值模拟结果的对比情况分别绘制成图4 和图5,将各模型实验与数值模拟结果列于表3。比较后发现:S-1圆管受压溃后呈现出混合变形模式,与实验结果相似性较强;压溃过程的力-位移曲线与实验所得曲线变化趋势吻合度较好,数值上存在差异,但偏差在可接受范围内。综上,所建立的有限元模型能够较好地反映结构变形模式受压溃时的载荷以及吸能情况,故可靠性较高。

图2 能量变化情况Fig. 2 Energy change

图3 薄壁管变形模式的实验与模拟对比情况Fig. 3 Comparison of experiment and simulation of four kinds of thin-walled tube deformation modes
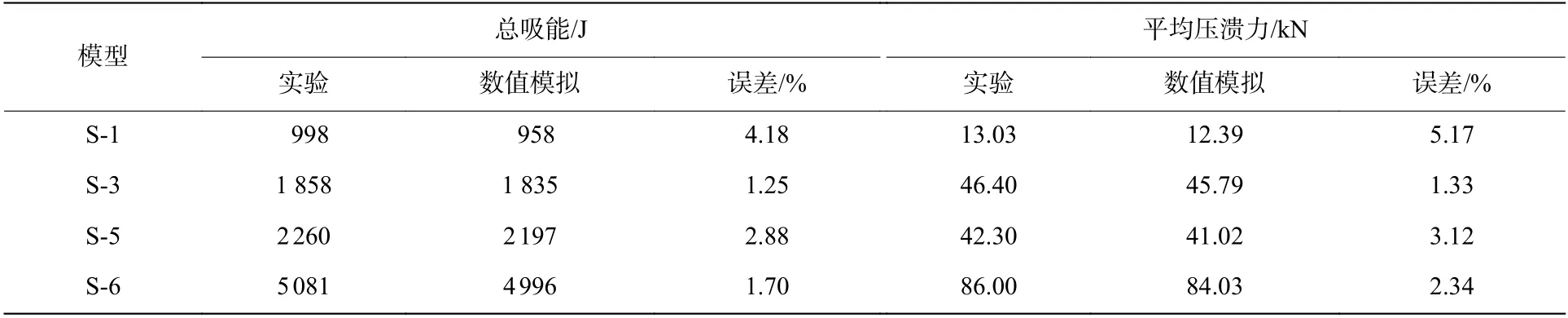
表3 实验与数值模拟结果对比Table 3 Comparison of experimental and simulation numerical results

图4 S-1 模型实验与数值模拟变形模式对比Fig. 4 Comparison of experiment and simulation deformation modes of S-1 model

图5 S-1 模型实验与数值模拟力-位移曲线对比Fig. 5 Comparison of force-displacement curves between experiment and simulation of S-1 model

表2 有限元验证模型尺寸参数[16]Table 2 Finite element verification model size parameters[16]
2 研究结果及讨论
吸能结构一般依靠其材料的变形来对外部冲击能进行吸收耗散,其性能一般由总吸能E、比吸能 δ 、初始峰值压溃力F0、平均压溃力F、压溃力效率 η 等指标进行衡量,同时对于类似落锤冲击的动态工况,还应考虑有效压溃长度l。着重关注比吸能以及有效压溃长度,并且期望薄壁管兼具高比吸能和较低的有效压溃长度,暨能够在一定质量下吸收更多冲击能,同时具备较强的轴向抗冲击能力,能够在更短的进程中使外部冲击物减速制动。各指标示意可见图6,计算式为:

图6 冲击过程中力-位移曲线Fig. 6 Force-displacement curve during impact

式中:F为压溃过程结构受力,m为结构质量。
2.1 薄壁管变形模式分析
构建等质量条件下正高斯曲率曲面(positive Gaussian curvature, PGC),零高斯曲率曲面(zero Gaussian curvature, ZGC)和负高斯曲率曲面(negative Gaussian curvature, NGC)等3 类曲率情况下的正方形(square, S)、六边形(hexagon, H)、八边形(octagon, O)和圆形(circular, C)横截面薄壁管,共计12 个。由于材料密度相同,使模型体积相同即可保证质量相同。
将其中某一模型沿纵向剖切,所得剖面的一半会产生两段曲线,将两段曲线进行数学表达及处理,之后将相应结构横截面面积S沿任意一条曲线方向进行积分即可求得其体积V。以NGC-S 模型为例,如图7 所示:沿纵向剖切得剖切面(红线所围区域),其上两曲线分别为y1,y2,则NGC-S 体积VNGC-S等于其横截面积SS沿任一曲线积分为:


图7 NGC-S 剖切面示意图Fig. 7 Schematic diagram of section plane of NGC-S
因此,求得各薄壁管横截面面积与边长a或半径r之间关系式关系式,即可进一步推得其体积:

为确保结构变形从初始受冲击端发生,进而获得完整变形形态,在薄壁管顶端添加长1.5 mm、与水平面呈37°角的斜坡触发结构[19],见图8。

图8 触发结构Fig. 8 Trigger structure
各模型冲击压溃后变形模式如图9 所示。首先从截面类型角度分析可知:正方形截面下的各结构呈轴对称模式,且产生的褶皱间距较大;六边形与八边形结构则表现出轴对称模式和混合模式;对于圆截面,只有NGC-C 结构表现为轴对称模式,其余均为混合模式。其次从高斯曲率类型角度分析可知:负高斯曲率情况下各结构均呈现轴对称模式;正高斯曲率结构中除PGC-S外均为混合模式;零高斯曲率情况下除ZGC-C外均为轴对称模式。由上述现象可知,当前工况下方形截面结构变形模式并不会随着高斯曲率类型的改变而改变。在负高斯曲率条件下这4 类不同截面类型薄壁管更易产生轴对称变形。

图9 变形模式对比Fig. 9 Comparison of deformation modes
各结构力-位移曲线如图10 所示,其中方形截面结构曲线在3 类曲率情况中均位于最下方,且其有效压溃长度最大。负高斯曲率情况下NGC-C 结构载荷波动程度较低且其有效压溃长度最小,如图10(a)所示。正高斯曲率结构中,PGC-C 结构载荷曲线位于PGC-H 以及PGC-O 之下,且初期载荷波动较大,如图10(b)所示。零高斯曲率结构中,ZGC-H 和ZGC-O 载荷变化趋势相似性较强且曲线明显位于ZGC-S 和ZGC-C 之上,如图10(c)所示。由上述现象可知,方形截面结构的吸能以及轴向抗冲击性较差,圆形截面结构在负高斯曲率下表现出了较小的有效压溃长度,能够在更短进程中使冲击墙制动,抗冲击性较好。

图10 3 类高斯曲率情况下的模型力位移曲线Fig. 10 Force-displacement curves of model under three kinds of Gaussian curvature
2.2 薄壁管吸能情况分析
为进一步探究各结构吸能特性,从力-位移曲线中提取各性能指标,将结果绘制成图11。分析可得,对于零高斯曲率情况下的各模型,其截面类型从四边形变化至六边形后,总吸能、比吸能、初始峰值力以及压溃力效率均大幅增加,有效压溃长度则显著减小,这是由于随着截面边数增加结构抗变形能力增强,变形区域增多,变形模式发生改变。但随着边数进一步增加至圆截面,性能指标差异逐渐减小,上述指标变化情况与文献[14]所得一致,其中ZGC-O 结构的比吸能和有效压溃长度最优,如图11(a)所示。上述由于截面边数增加所产生的指标变化情况同样在正高斯曲率和负高斯曲率情况下出现,但在正高斯曲率组中PGC-H 结构的比吸能和有效压溃长度最优,如图11(b)所示。负高斯曲率组中NGC-O 结构的比吸能最优;NGC-C 的有效压溃长度指标最优,如图11(c)所示。

图11 3 类高斯曲率情况下的模型性能指标比较Fig. 11 Comparison of model performance indexes under three kinds of Gaussian curvature
为在3 组模型中实现结构优选,鉴于文献[20]的成功经验,本文中借助复杂比例评估法(complex proportion assessment,COPRAS)首先对比吸能、有效压溃长度、初始峰值力和压溃力效率四项性能指标进行了权重分配,其次对各结构进行了综合性能评分,从而实现针对各结构的客观评价以及准确择优,COPRAS 法流程如图12 所示,图中:wj代表性能指标的权重因子;S+、S-分别代表有利值和不利值;Qi、Ui分别代表综合性能评分和相对分值,Ui越大说明该结构综合性能越好。

图12 COPRAS 法流程图Fig. 12 Process flow chart of COPRAS method
由于本文中期望性能优异的吸能结构应兼具高比吸能和低有效压溃长度,因此考虑指标 δ 、l同时享有最高优先级,其次为 η 、F0。根据COPRAS 法,高优先级指标与低优先级指标对比时,前者赋3 分,后者赋1 分;相同优先级对比时,二者各赋2 分,最终将各指标得分数据统计运算后给出权重因子wj。上述4 项性能指标的权衡赋分过程以及被分配的权重因子wj列于表4,各结构通过COPRAS 法所获取的相关计算值以及最终综合性能排名情况列于表5。

表4 指标 δ 、l、F0、η 的权衡赋分过程及其权重因子w jTable 4 Weighing and scoring process of four indicators ( δ , l, F0, η ) and their weighting factors ( w j )

表5 各结构COPRAS 法相关计算值Table 5 Relevant calculated values of COPRAS method for each structure
COPRAS 法分析结果表明,NGC-C 结构在3 组模型中综合性能最优,其次为ZGC-O 和PGC-H。
为进一步分析NGC-C 结构各项性能指标,将NGC-C、PGC-H 和ZGC-O 三者的力-位移曲线绘制成图13(a),发现NGC-C 有效压溃长度最小,载荷波动程度最小。从曲线中提取出各项性能指标,绘制成图13(b),发现NGC-C 结构的比吸能比ZGC-O 高0.1 %,比PGC-H 低0.6 %。但有效压溃长度比ZGC-O低12.0%,比PGC-H 低15.0%。可知在相同工况下若压溃相同距离,NGC-C 结构具备较大能量吸收潜力。进一步地,利用应变云图来表现NGC-C 受轴向冲击后所发生的变形情况,并取ZGC-O 为对照,如图15 所示。其中褶皱波长定义及计算方法参照文献[21],褶皱波长越小说明结构对于冲击能吸收越充分,吸能效率越高。其次引入平均应变值来衡量结构综合应变程度,相同工况下该值越大说明结构变形程度越大,能够吸收更多冲击能,平均应变值根据总应变与单元总数相除得出:

图13 各组优选模型结果比较Fig. 13 Comparison of optimal model results of each group

式中:b为单元平均应变值,εi为第i个单元所产生的应变值,n为单元总数。
比较后发现,NGC-C 结构变形区域形状为条带状,对应轴对称变形模式下所产生的均匀褶皱,褶皱波长均值为25 mm,b=0.118,如图14(a)所示;ZGC-O 结构变形区域主要集中在8 条棱边上且轴向分布不均匀,同样存在条带状变形区域,褶皱波长均值为33 mm,吸能情况很大程度受棱边数量的影响,同时b=0.103,如图14(b)所示。因此,NGC-C 结构单元平均应变值更大,褶皱波长更小。综合以上分析可知,NGC-C 结构具有吸能效率高,轴向抗冲击性好等优点,更适合作为能量吸收结构。

图14 NGC-C 与ZGC-O 结构的应变情况Fig. 14 Strain of NGC-C and ZGC-O structure
3 薄壁圆管优化设计
3.1 代理模型建立
步骤1:优化问题。以比吸能最大化和有效压溃长度最小化为优化目标,参数T、G、R为优化变量,参考薄壁管定义(外径与壁厚之比大于20),规定参数T、G、R取值范围分别为1~5 mm、-10~10 mm、60~100 mm。综上,优化问题为:

步骤2:样本点选取。为确保优化变量取值范围的全覆盖,采用拉丁超立方抽样法进行样本点选取,并获取各样本点的响应值,如表6 所示。

表6 样本点及其响应Table 6 Sample points and responses

表6(续)Table 6 (Continued)
步骤3:响应面代理模型建立。鉴于文献[22]中的成功案例,采用多项式响应面代理模型表达出设计变量与响应之间的关系。为验证代理模型的准确性,采用调整后的拟合优度系数R2Adj来衡量,该系数越接近1 说明模型准确性越好,具体模型表达式如下:

3.2 优化结果及讨论
基于上述代理模型,借助改进非支配排序遗传算法(NSGA-Ⅱ)进行多目标优化。优化后所得出的非劣解组成了帕累托解集,该解集在空间上形成了帕累托前沿(Pareto front)。为从解集中选取最合适的解,使用最小距离法得到最优点B,如图15 所示。该点对应最优解为T=2.56 mm、G=-9.71 mm 和R=75.48 mm,对应的响应值 δ =26.24 J/g、l=69.29 mm。根据最优解参数建立有限元模型,将所得数值模拟结果与上述代理模型预测结果进行对比,对比结果见表7。比吸能和有效压溃长度的数值模拟与预测结果相对误差均在5%以内,优化结果准确度较高。相较于2.2 节中通过COPRAS 法评定的最优NGC-C 结构,优化后所得出的NGC-C 结构的比吸能提高了16.47%,有效压溃长度降低了12.4%,同时结构质量降低了20.18%。设计人员可通过更改 α 角来改变比吸能与有效压溃长度的权重,进而选取能够满足工艺性能需求的最优解。

图15 Pareto 解集Fig. 15 Pareto solution set
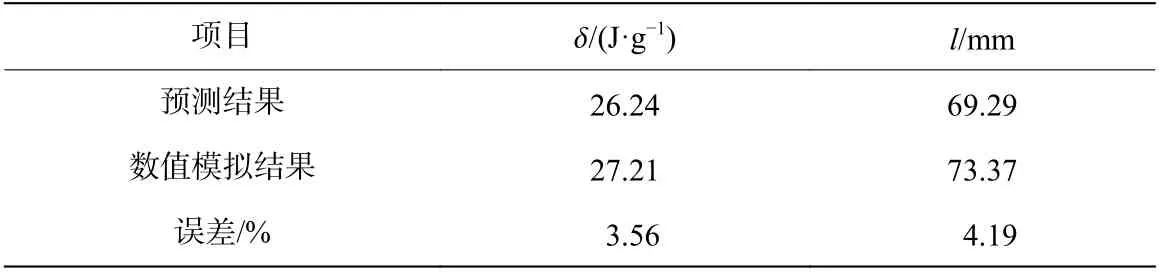
表7 数值模拟与代理模型预测结果对比Table 7 Comparison of simulation and agent model prediction results
4 结 论
本文中提出了一种负高斯曲率薄壁吸能结构,通过文献验证有限元模型的可靠性,对其进行轴向动态冲击模拟,分析了该结构的吸能特性。借助COPRAS 法将其与各类非负高斯曲率薄壁结构进行了性能对比。最终利用拉丁超立方抽样法构建样本空间,借助响应面法建立代理模型,通过NSGA-Ⅱ遗传算法求解出最优解集,对设计参数进行了优选,主要结论如下。
(1)通过数值模拟对薄壁圆管进行动态轴向压溃所得出的力-位移曲线和变形模式均与文献中相应结果一致性较好,所建立的有限元模型的可靠性较高。
(2)在等质量条件下与各类非负高斯曲率薄壁结构比对后发现,负高斯曲率圆管综合性能最优。相同动态冲击工况下,该结构能够在更短的进程中使冲击墙制动,同时能够吸收更多的冲击能,故其较适合作为能量吸收结构。
(3)优化后负高斯曲率圆管结构的比吸能提高了16.47%,有效压溃长度降低了12.40%,同时结构质量降低了20.18%。设计人员能够根据不同工艺性能要求,从最优解集中选取最适合的设计参数组合。

