基于周期性半模型的中低速磁浮用直线电机的性能计算分析

王 禹，李伟业，罗英露，黄德聪，黄直峰，陈 财

（1.中车株洲电力机车研究所有限公司，湖南 株洲，412001；2.襄阳中车电机技术有限公司，湖北 襄阳，441057）

0 引言

采用直线感应电机可使列车不受轮轨黏着制约，提高列车爬坡能力，减小列车转弯半径，降低列车维护成本。因此，近年来直线感应电机在轨道交通，尤其是中低速磁浮交通领域得到广泛应用［1］。直线感应电机的性能计算主要采用磁路法、二维有限元法、三维有限元法等手段。但是由于直线感应电机结构特殊，在其性能计算方面仍然存在较多难点。如：直线感应电机初级与次级宽度不同，且一般电机初级宽度小于次级宽度，为了克服横向边端效应，直线电机次级感应板形状一般为杯状，导致电机在宽度方向上不对称；与旋转电机不同，电机的转子即直线电机次级感应板，其长度远大于电机初级长度，近似为无限长，在有限元计算中建模难度较大。

在直线感应电机电磁性能计算方面，学者们展开了相关研究。文献［2］通过电磁场解析法及三维有限元仿真法对双边直线感应电机电磁性能进行了计算，但为了减小计算量在其三维模型中没有考虑绕组端部，并忽略了横向端部效应，这样会导致分析时产生一定误差。文献［3］对城轨交通直线感应电机电磁性能进行了分析，采用了瞬态三维仿真方法；由于仿真时间过长，计算推力及法向力没有达到稳定。文献［4］为了缩短计算时间，减小了次级长度，并使用零矢量边界条件，因此该模型只能用于评估静态电磁性能。文献［5］在文献［4］的基础上延长了仿真周期，通过三维有限元仿真计算了次级间断对直线电机电磁性能的影响；但是由于采用零矢量边界条件，次级感应板长度有限，该方法只能计算低速工况下的电机电磁性能，且计算量大、计算时间长。

磁路法、二维有限元法在数学模型上无法完全等效实际电机模型，需要对计算过程或计算结果进行修正，对设计经验要求较高。三维瞬态仿真中的电机模型理论上可以与实际电机完全一致，如考虑了绕组端部形状、感应板延长弯折部分、感应板无限长等，具有磁路法计算及二维仿真无法达到的准确性；但是目前直线感应电机三维瞬态仿真研究相对较少且不完善。造成这种现象的主要原因包括：（1）中低速磁浮用直线电机模型尺寸较大，一般初级长度为2 m左右，次级感应板实际长度远大于初级的，而电机气隙长度及感应板厚度为毫米级，剖分后会产生数量庞大的网格，对计算资源要求极高；（2）与旋转电机不同，直线电机运动范围大，且性能随速度变化较大，需要较大的模型范围供初级运动，也将导致网格数量庞大，计算困难。此外，目前已公开文献中涉及因温度通过影响感应板特性进而影响电机特性的研究较少，这也影响了性能计算的准确性。

本文针对以上中低速磁浮直线感应电机性能计算中的难点，分别采用磁路法、二维有限元法及三维有限元法进行性能计算，并提出采用周期性半模型三维有限元仿真方法，在保证计算精度不变的前提下提高了计算速度和性能计算效率，为三维有限元仿真在直线感应电机设计中的工程化应用奠定基础；最后，搭建了直线电机静态测试平台，对计算数据与测试数据进行分析。

1 直线感应电机性能计算磁路法

与旋转感应电机相似，直线感应电机的电磁性能可以通过等效电路模型计算［6］。图1所示为Duncan提出的直线感应电机并联等效电路，其中R1为初级相电阻［7］，其计算如式（1）所示；图2为直线电机结构。

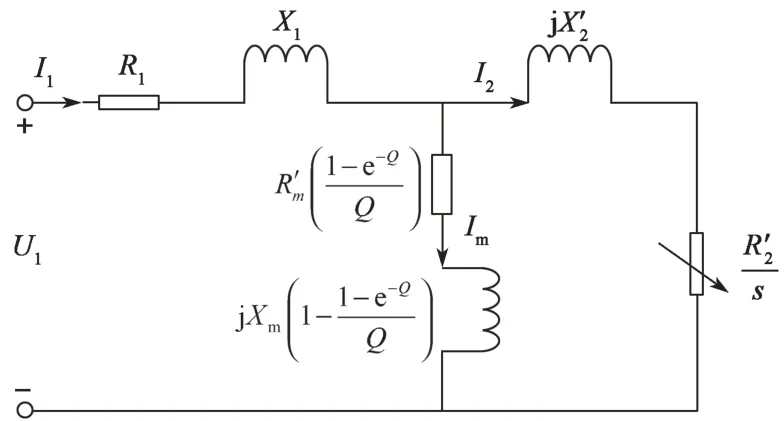
图1 直线感应电机Duncan等效电路Fig.1 Duncan equivalent circuit of linear induction motor

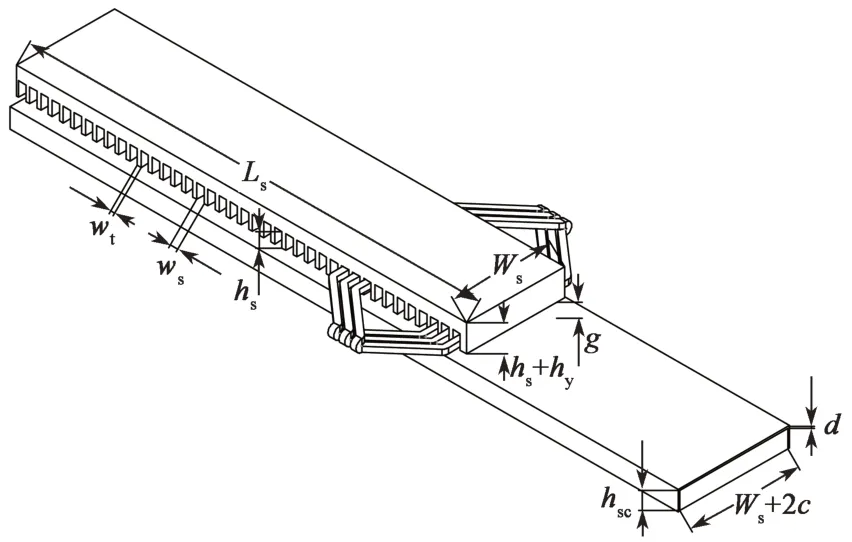
图2直线感应电机结构模型Fig.2 Structure model of linear induction motor

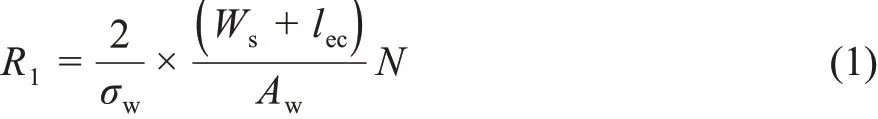
式中：σw——初级绕组导体电导率；lec——初级绕组端部长度；Ws——初级铁心宽度；N——初级绕组每相串联匝数；Aw——初级绕组导体截面积。

初级侧定子漏抗X1［7］如式（2）所示。

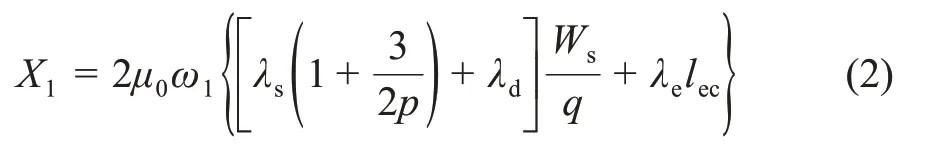
式中：μ0——真空磁导率；p——电机极对数；q——每极每相槽数；ω1——初级角频率；λs——槽比漏磁导；λd——端部漏磁导；λe——谐波漏磁导。

每相励磁电抗通过式（3）计算［7］。

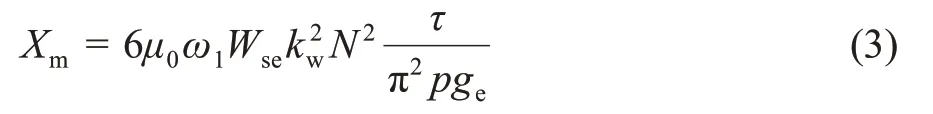
式中：kw——绕组系数；τ——直线感应电机极距；Wse——初级铁心等效宽度；ge——气隙等效长度。

其中：

式中：gm——电磁气隙；kl——气隙漏抗系数；kc——卡特系数；ktm——边缘效应引起的磁阻系数；ks——次级铁心饱和系数［8-10］；g——机械气隙；d——次级感应板厚度；c——次级单边超出初级铁心长度；τs——初级槽距；G——电机的品质因数；f1——初级供电频率；δi——次级铁心磁场透入深度；μi——通过迭代算法计算的次级铁心磁导率。

对于次级铁心，由于边端效应的影响，需要对次级铁心材料电导率进行折算［11］。

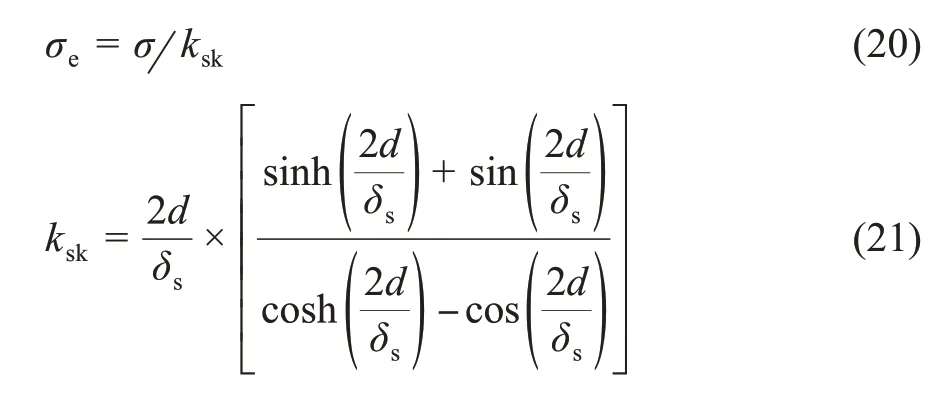
式中：σ——次级导电铝板电导率；δs——次级铝板的磁场透入深度，可以通过式（22）计算。

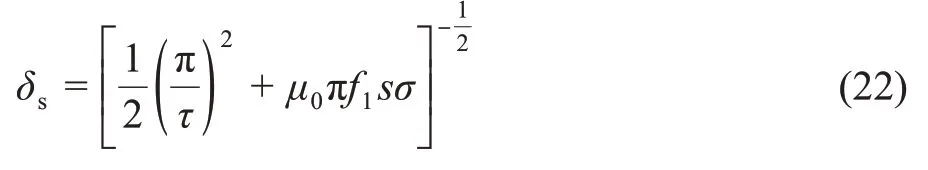
由于次级导电板存在集肤效应，其电导率通过ksk进行折算，边缘效应导致的电导率变化通过系数ktr进行折算。如果将次级铁心中的电流传导也考虑进去，那么其等效电导率由式（23）计算［8-10］。

式中：σi——次级铁心电导率。

次级折算到初级侧的电阻为

式中：Ge——修正后的品质因数。

对于直线感应电机，次级漏抗可通过式（26）～式（29）进行计算［9-10］。

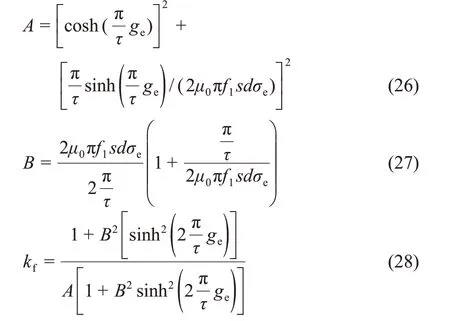
Q是标幺化的电机长度，可以通过式（30）进行计算［7］：

式中：Ls——初级侧长度；vr——电机运行速度；Lm——励磁电感；L'2——次级漏感。

气隙磁密可以通过式（31）计算［7］：

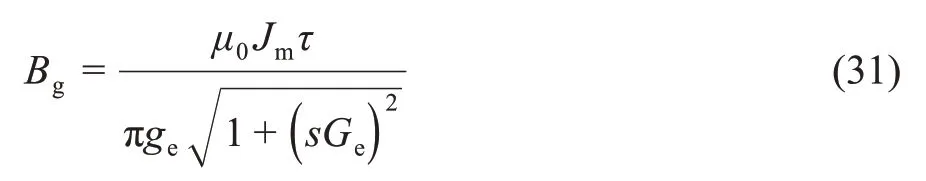
式中：Jm——等效电流层幅值［7］。

式中：I1——相电流。

根据等效电路可以计算出电机输出的牵引力Fx：

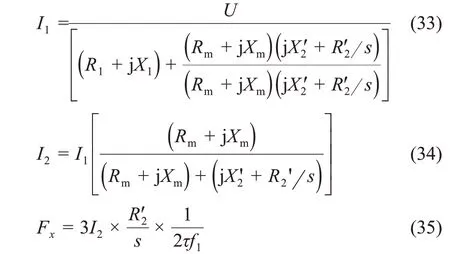
电机法向力F y可以通过式（36）计算［7］。

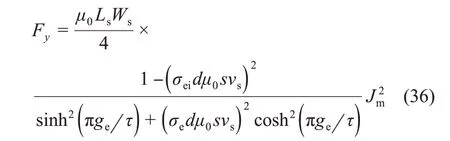
式中：vs——同步速度。

2 直线感应电机性能计算有限元法

2.1 二维有限元模型

本节针对一款中低速磁浮直线感应电机进行二维及三维建模，并对其进行基于有限元法的三维仿真研究，所研究电机的基本参数如表1所示。图3给出了直线电机起动点二维仿真磁密分布云图，计算输入电流为450 A，感应板温度为60℃、电导率为32 500 000 S/m，转差频率为15 Hz，电机运行速度为0。

图3 直线电机二维模型起动点磁密分布Fig.3 Flux density distribution of the linear induction motor at starting point by 2D model

表1 直线电机基本参数Tab.1 Basic parameters of the linear induction motor

二维模型只能描述沿电机运动方向的几何模型，不能反映垂直于运动方向的几何模型，因此无法考虑横向边端效应对电极性能的影响，但可以通过感应板等效电导率对计算结果进行修正，并通过式（23）计算材料的等效电导率。修正后的牵引力及法向力仿真结果如图4所示，稳定后的牵引力为3.74 kN，稳定后的法向力为1.91 kN。

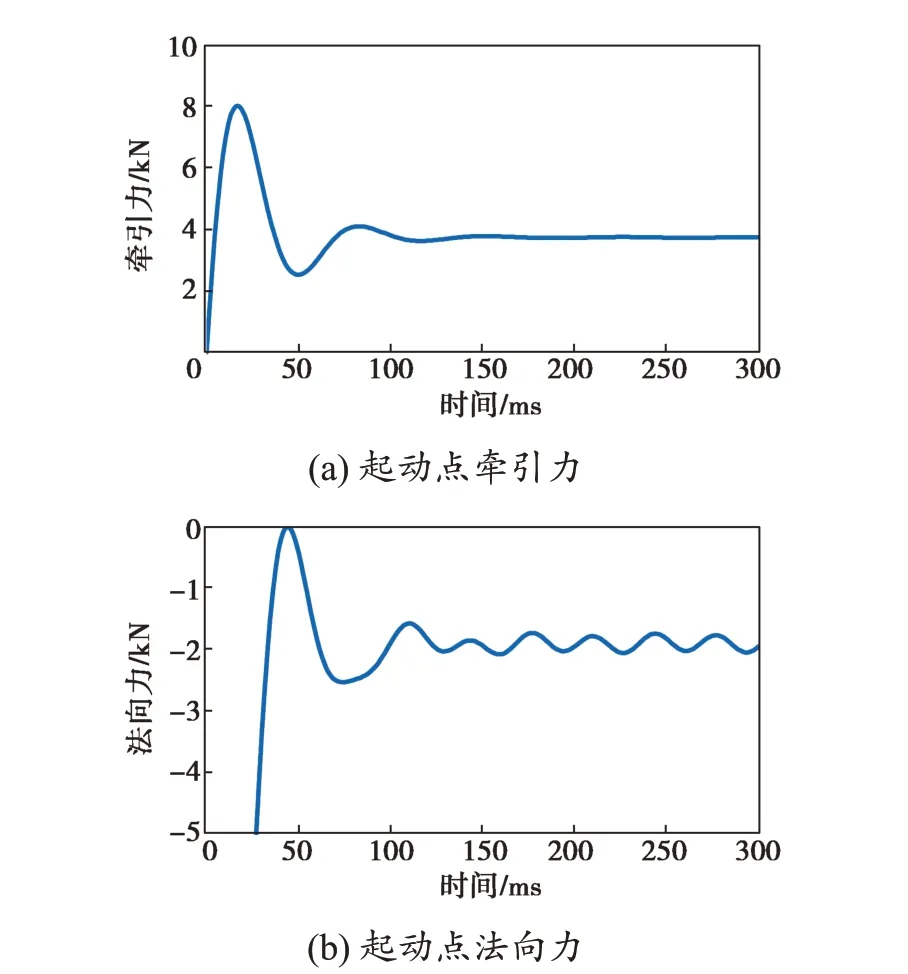
图4 直线电机二维模型有限元仿真结果Fig.4 Simulation results of the linear induction motor by 2D model

2.2 三维有限元模型

为了使仿真模型更加接近实际电机，建立了直线电机三维周期性全模型并进行有限元仿真。与二维模型相比，三维周期性全模型对电机绕组端部进行了建模，其感应板宽度与实际电机的一致，次级感应板铝板形状与实际电机的一致，均为杯状，其磁密分布如图5所示。在有限元求解过程中，在次级感应板左右两侧施加了周期性主从边界条件，这样可以将次级感应板等效为无限长结构，与实际情况一致。仿真模型网格数量达到了3 360 000，求解时长达到了4 h 13 min；由于仿真工况点为起动点，电机工作频率较低，牵引力稳定较快；如果进行高速段仿真，计算网格需要加密，计算结果稳定较慢，求解时间会继续增加。直线电机在实际工程应用中需要进行多工况计算，而目前的求解时间很难满足工程化需求。

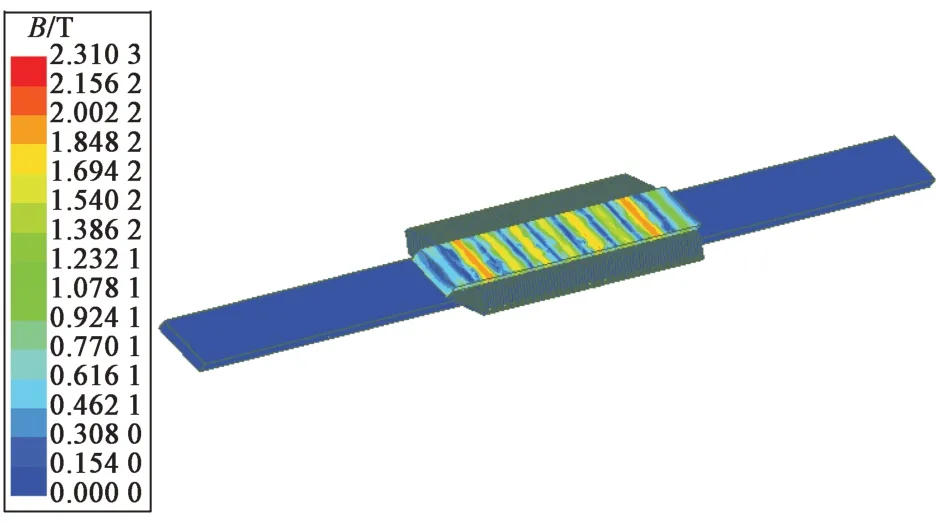
图5 直线电机三维周期性全模型起动点磁场分布Fig.5 Flux density distribution of the linear motor at starting point by 3D whole model

为了提高求解速度、缩短求解时间，需要将模型进行简化。直线感应电机沿运动方向轴对称，因此可以将模型简化为半模型，在有限元计算中保持全模型中的周期性主从边界条件不变，重点是电流激励不能落在中心切面上，需要将电流面沿导体移动一小段距离，这样电流激励会保持在导体中而不会流入空气。图6所示为周期性半模型起动点磁密分布，图7为三维模型剖分网格。为了保证计算精度，对次级感应板网格进行了加密，网格数量为1 840 000，求解时长为2 h 32 min，仿真时间缩短了约40%，直线电机三维半模型与全模型仿真数据如表2所示。

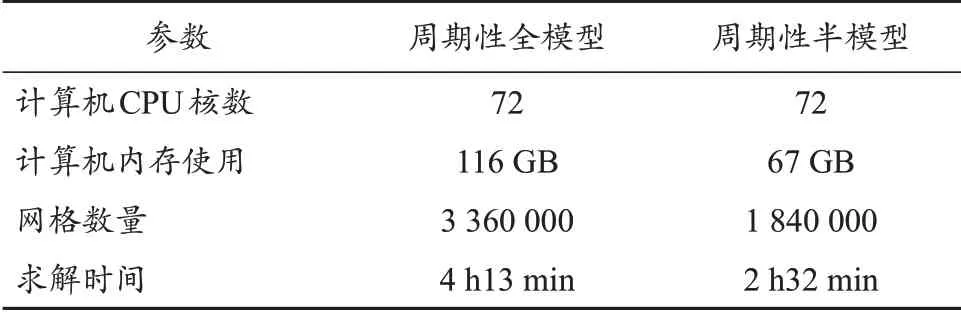
表2 直线电机三维半模型与全模型仿真数据对比Tab.2 Simulation parameter comparison between the half model and whole model for linear motor

图6 直线电机三维周期性半模型起动点磁场分布Fig.6 Flux density distribution of the linear motor at starting point by 3D periodic half model

图7 直线电机三维有限元仿真剖分Fig.7 Mesh of the EMF mode for linear motor

分别计算得到半模型和全模型起动点牵引力曲线（图8），可以看出，使用半模型计算的起动点牵引力与全模型计算的起动点牵引力完全吻合，曲线稳定后牵引力均为4.11 kN。通过计算分别得到半模型和全模型起动点法向力曲线（图9），可以看出，使用半模型计算的起动点法向力与全模型计算的起动点法向力完全吻合，曲线稳定后法向力均为2.00 kN。通过对比以上仿真结果可以认为，周期性半模型可以完全替代周期性全模型，在保证仿真结果一致的前提下减少运算时间。

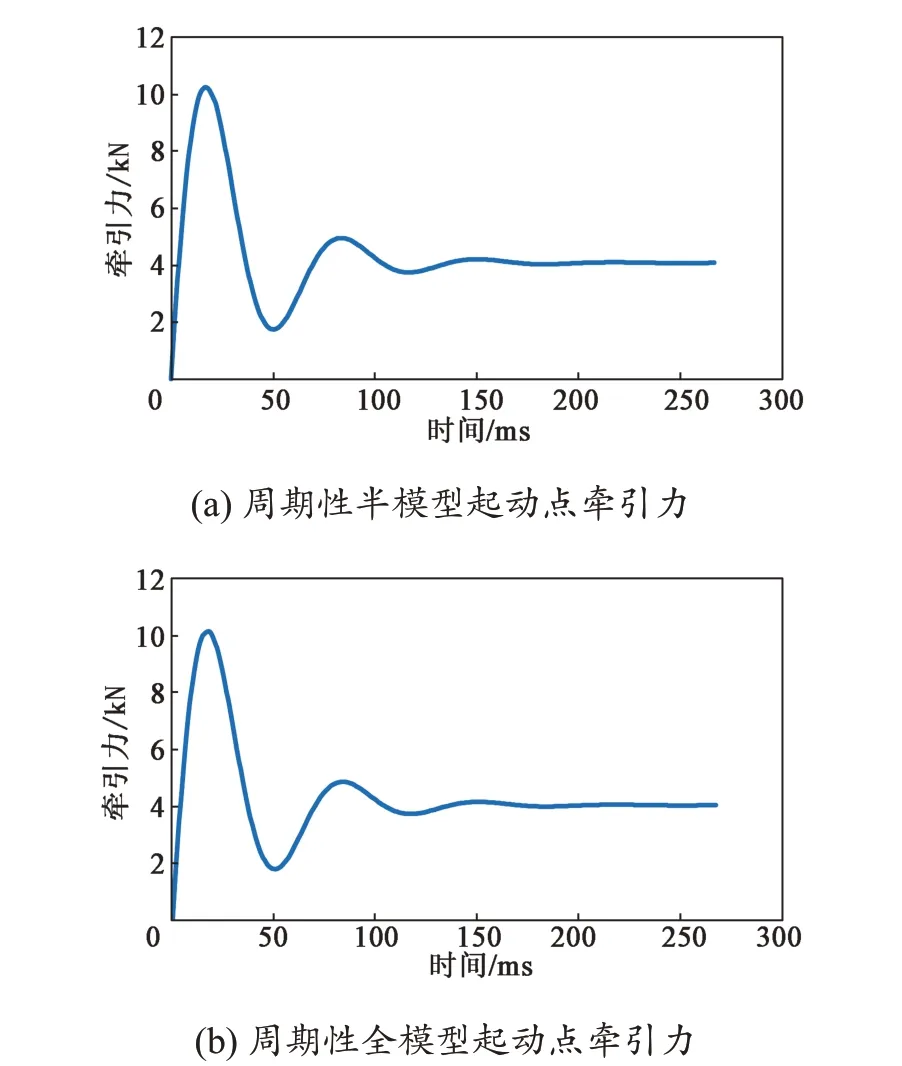
图8 直线电机牵引力三维有限元仿真结果对比Fig.8 Simulation result of thrust of the linear motor by 3D model

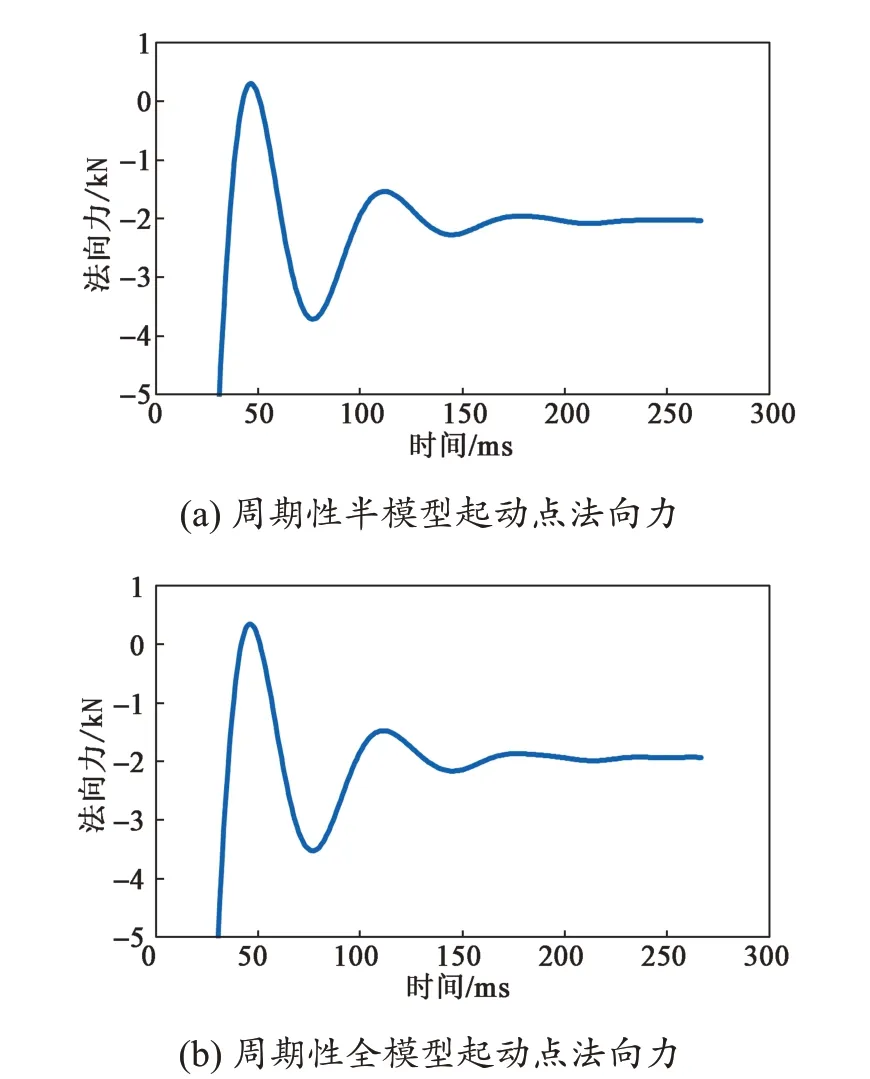
图9 直线电机法向力三维有限元仿真结果对比Fig.9 Simulation result of normal force of the linear motor by 3D model

3 试验验证

为了测试直线电机静态特性，搭建了直线电机试验台架，试验现场如图10所示，试验系统包括被测直线电机、感应板、冷却风机、变流器、拉力传感器、压力传感器和数据采集装置等。将直线电机的初级安装于静止试验台上，调节初级与感应板的气隙，使之达到要求值，并通过与直线电机配套的逆变器供电。测量电机的频率、牵引力、法向力、电流、电压、基波功率因数、输入功率。试验时调整电机的气隙值，试验中气隙的取值分别为9 mm和13 mm，电机的额定气隙为13 mm。将测力传感器负载端与初级一端固定，沿着与感应板水平方向均匀缓慢地向前推动（或拉动）测力传感器。直到初级与感应板开始产生相对位移，读取测力传感器的读数，测试3次取其平均值。将初级与测力传感器一端相连，传感器另一端与测试台的构架固定，保持传感器水平方向受力，并施加适当的预推力，以防止对传感器造成冲击，然后启动直线电机，及时记录牵引力、电压、电流、功率等参数。

图10 测试现场Fig.10 Test platform

利用本文中给出的磁路法、二维有限元法、三维有限元方法分别对磁浮直线感应电机进行了不同气隙下起动点性能计算，计算结果及测试结果如表3所示。通过计算结果与测试结果对比分析可知，磁路法牵引力计算结果与二维有限元法的相近，与前文的原理分析结果一致；三维有限元法的计算结果与实际测试结果相近，计算准确性较高。磁路法与二维有限元法的计算结果虽然误差相对较大，但仍可用于快速评估及特性曲线计算等场景，周期性半模型三维有限元法可以用于性能的精确评估与方案优化。4种方法计算的法向力与试验测试值均有一定偏差。影响法向力的因素较多，如直线电机及感应板静态测试时可以等效为电机短路状态，因此感应板及背铁温度升高较快，在法向力的作用下电机初级及次级都会发生一定形变，导致气隙变小，影响测试结果；其次，随着温度的变化，材料特性会发生一定程度的改变，而仿真模型中仅能考虑温度对材料电阻率的影响，无法全面考虑材料属性改变的影响。后续将在测试台的刚度和材料特性的准确性两个方面进行改进。

表3 电机电流450 A时牵引力及法向力Tab.3 Thrust and normal force of the linear motor at 450 A

4 结语

本文针对中低速磁浮直线感应电机分别进行了磁路法、二维有限元法、三维有限元法性能计算研究，并搭建了测试平台，对计算结果进行了验证。通过对计算数据与测试数据的对比分析得出，3种计算方法可在电机设计的不同阶段使用，以实现电机设计快速与准确兼顾的目的。本文提出的周期性半模型三维有限元法兼顾了计算准确性及计算速度，且随着有限元求解方法的不断改进及计算设备性能的不断提升，该方法的实用性会进一步增强，可实现电机设计全流程的三维仿真，并提高性能计算准确性。