基于模糊神经网络的重载列车空气制动力预测方法

史 可，张征方，白金磊，蒋 杰

（1.中车株洲电力机车研究所有限公司，湖南 株洲 412001；2.株洲中车时代电气股份有限公司，湖南 株洲 412001）

0 引言

目前我国铁路货运主要采用重载运输的方式实现。重载列车运行过程中，通常需要处理长达十几公里或者几十公里的长大下坡道的制动问题，此时需要采用循环空气制动的方式进行速度控制，因此循环空气制动是当前研究的热点和难点。空气制动力的强弱与多种因素有关，若不能兼顾各种因素的影响，就会造成列车制动系统中的管路存在压力梯度，导致列车动力不足、制动力不断衰减，出现超速、车钩断裂等现象，严重时列车将有脱轨危险，这种现象在列车采用循环空气制动时尤为突出［1-2］。

对于空气制动，国内外学者已经进行了大量研究。国内，大连交通大学建立了基于空气流动理论的空气制动数值仿真系统，对列车制动系统的管路及缸室的气体瞬态特性进行计算，进而预测2万吨组合列车的紧急制动和常用制动特性［3］；西南交通大学的张军磊利用AMEsim软件建立了重载列车制动系统模型，对重载列车分配阀、紧急阀、中继阀、换向阀及双向阀等结构进行了仿真分析，研究了各阀制动性能的影响参数，对常用制动模式和备用制动模式下的初制动、常用制动、抑制位制动、重联位制动和紧急制动等工况进行了仿真，并与试验结果进行对比，获得了较满意的仿真效果［4］。国外，波兰的Tadeusz Piechowiak在考虑了多种动力学因素的情况下，建立了空气制动系统模型，并采用不同精度的仿真模型进行了验证［5］。意大利的Cantone L，Crescentini E等人开发了传统货运列车空气制动系统数值模型，进行了紧急制动、常用制动、阶段制动及缓解等工况的测试，并对测试结果与试验数据进行了对比，证明了该模型的有效性［6］。但是，上述研究普遍采用重载列车的物理模型，并缺乏有效的非线性控制策略［7］，存在以下缺点：（1）利用重载列车的机理关系搭建的物理模型，对具有强非线性、大时滞性的重载列车而言并不准确；（2）对于影响重载列车循环空气制动力强弱的因素缺乏系统性的研究，难以使用合适的非线性控制策略实现对空气制动力的精确预测。

针对重载列车循环空气制动力精确预测这一难题，本文提出了一种基于模糊神经网络（fuzzy logicbased neural network，FLNN）的空气制动力预测方法。其首先选取与重载列车空气制动强相关的参数作为训练样本，设计径向基神经网络（radial basis functionneural network，RBF-NN）对现场数据样本进行训练，得到模糊逻辑形式的空气制动力离线预测规则。然后，计算当前数据与空气制动力离线预测规则的匹配度，得到相应的预测规则并输出空气制动力预测值，从而达到空气制动力的精确预测效果。

1 重载列车空气制动系统模型

本文研究对象为由HXD1型大功率电力机车牵引的重载列车，其空气制动系统的空气管路与制动系统主要由风源系统、制动机系统和其他气动辅助装置组成。重载列车的空气制动是个复杂的过程，其影响因素很多，在大量试验过程中，除了重载列车自身参数以外，空气制动力还和以下特征参数有关，分别为空气制动施加速度、减压量、电牵引/制动力、大闸减压量、小闸减压量及流量计。

为预测空气制动中空气制动力的准确性，根据《牵引计算规程》描述的空气制动模型计算实际空气制动力Fa：

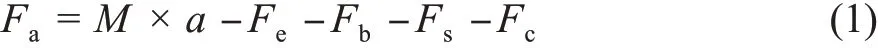
式中：Fe——列车牵引/电制动力；M——列车质量；a——列车加速度；Fb——基本阻力；Fs——坡道阻力；Fc——弯道阻力。

为完成对重载列车空气制动力的预测，实现基于FLNN的空气制动系统离线数据训练，将重载列车空气制动系统模型的输入矩阵定义为Λ=[δ1δ2δ3δ4δ5δ6]，其中δ1～δ6分别对应施加速度、减压量、电牵引/制动力、大闸减压量、小闸减压量、流量计；将模型输出定义为空气制动力Fa。

2 基于FLNN的空气制动力预测方法

本文所提出的基于FLNN的空气制动力预测方法（图1），其从空气制动模型和空气制动力预测计算两个方面提高精度，实现重载列车空气制动力的精确预测；设计了基于RBF-NN的空气制动力模糊预测规则训练过程，通过对大量离线空气制动样本数据的分析和处理，解决了传统空气制动模型面对的强非线性和大时滞性难题；所提出的空气制动力模糊预测规则匹配度计算方法，可匹配到当前对应的空气制动力模糊预测规则，具有覆盖全线路全工况的特点，提高了空气制动力的预测精度。

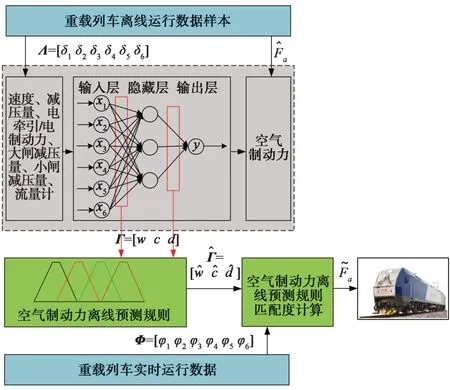
图1 基于FLNN的重载列车空气制动力预测方法框图Fig.1 Block diagram of FLNN based air braking force prediction method for heavy haul train

2.1 基于RBF-NN的空气制动力模糊预测规则训练

本节从重载列车空气制动系统模型的特征角度出发，利用重载列车空气制动特征参数，实现基于RBF-NN的空气制动力模糊预测规则训练［8-10］。RBF-NN的输入为空气制动特性参数δ1～δ6，RBF-NN的输出为空气制动力实际值F̂a。所设计的RBF-NN结构如图2所示，基于RBF-NN的空气制动力模糊预测规则［11-13］的训练步骤如下：

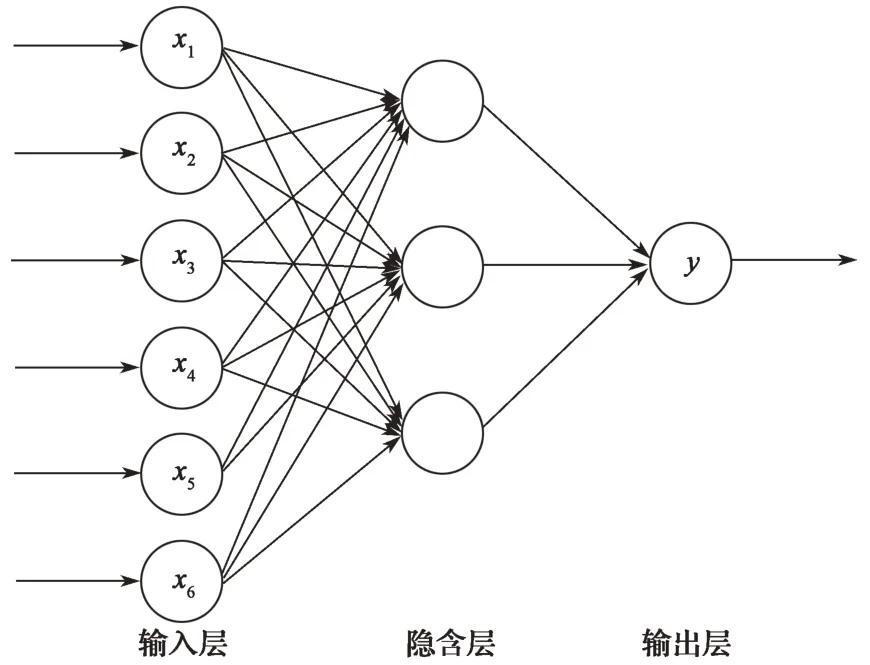
图2 RBF-NN结构框图Fig.2 Block diagram of RBF-NN

（1）确定参数。输入向量X=[x1x2…x n]T，n是输入层单元数；输出向量Y=[y1y2…y q]T，q是输出层单元数；希望输出向量O=[o1o2…o q]T；初始化隐含层至输出层的连接权值W k=[w k1wk2…wkp]T，其中，k为输出个数，k=1，2，…，q，p为隐含层单元数；初始化隐含层各神经元的中心参数C j=[c j1c j2…c jn]T，j为隐含层神经元个数；初始化宽度向量D j=[dj1dj2…djn]。

（2）计算隐含层第j个神经元的输出值z j。

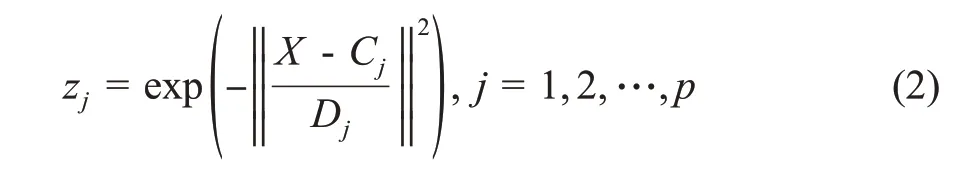
（3）计算输出层神经元的输出。

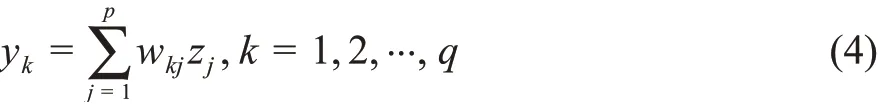
（4）权重参数的迭代计算。

本文中RBF-NN权重参数的训练采用梯度下降法。中心、宽度和权重参数均通过学习来自适应调节到最佳值，迭代计算公式为

式中：η——学习因子；E——RBF-NN的评价函数，E=其中O lk——第k个神经元在第l个输入样本时的期望输出值，y lk——第k个神经元在第l个输入样本时的网络输出值；α——误差调整因子。

（5）计算网络输出的均方根误差。

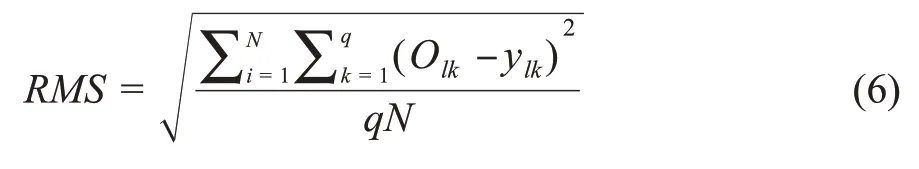
式中：N——输入样本个数。

若RMS≤ε，其中ε为迭代终止精度，则训练结束；否则，转到步骤（3）。

2.2 空气制动力模糊预测规则匹配度计算

在2.1节中，RBF-NN训练出的空气制动力模糊预测规则Γ=[w c d]为式（5）中RBF-NN的权重值的集合。该空气制动力模糊预测规则具有离线特征且针对全工况，但并不具有自适应性。因此，需要根据当前空气制动特征参数实际值进行匹配度计算［14］，找到与当前空气制动最匹配的在线空气制动力模糊预测规则，其原理如图3所示，输入是当前空气制动特征参数实际值Φ=[φ1φ2φ3φ4φ5φ6]和空气制动力模糊预测规则Γ=[w c d]，输出是当前空气制动力模糊预测规则

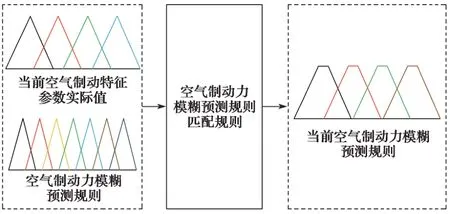
图3 空气制动力模糊预测规则匹配度计算结构框图Fig.3 Block block diagram of matching degree calculation of air braking force fuzzy prediction rules

具体的匹配度计算方法如下：

式中：δi——2.1节中定义的空气制动特征参数；φi——2.2节中定义的当前空气制动特征参数实际值。

由此可以找到当前空气制动力模糊预测规则̂对应的下标，进而找到

2.3 基于FNN的空气制动力预测

基于FNN的空气制动力预测原理如图4所示。完成基于RBF-NN的空气制动力模糊预测规则训练和空气制动力模糊预测规则匹配度计算后，得到当前空气制动特征参数实际值Φ=[φ1φ2φ3φ4φ5φ6]和当前空气制动力模糊预测规则将Φ输入到，通过计算得到预测空气制动力͂，完成对重载列车空气制动力的预测。

图4 基于模糊神经网络的空气制动力预测结构框图Fig.4 Block diagram of air braking force prediction based on fuzzy neural network

3 试验验证

为了验证所提方法的有效性，本文采集大秦铁路涿鹿到茶坞区间大长下坡道循环空气制动数据进行分析。

大秦铁路是中国华北地区一条连接山西省大同市与河北省秦皇岛市的国铁I级货运专线铁路，也是中国境内首条双线电气化重载铁路和首条煤运通道干线铁路。大秦铁路全线地形复杂，桥隧相连，桥梁、隧道和涵洞的长度占线路总长的30%，其中“涿鹿到茶坞”区间为大长下坡道，区间最大坡度-12‰，平均坡度-9‰，在该区段运行时必须采用循环空气制动的方式进行调速控制［15］。

3.1 试验参数设置与分析

本文主要分析循环空气制动的调速闸，不考虑停车闸和车辆静态下施加的闸。列车编组形式为“1+1”编组，货车辆数为210，总重21 000 t，载重16 800 t。

为了验证所提方法的有效性，分别采用涿鹿到茶坞区间的连续3次空气制动以及单次循环空气制动的数据进行验证。在实际工程中，由于空气制动产生的制动力一般在1 000 kN以上且具有较大的变化，如果能将空气制动力的预测误差集中在100 kN以内，就认为具有较好的预测效果。

3.2 试验1

试验内容：在涿鹿到茶坞区间K134+775至K178+214段，连续3次空气制动。

该试验的空气制动力预测效果和预测误差分别如图5和图6所示。对图中数据进行分析，预测误差区间分配如表1所示。由数据分析可知，采用基于FLNN的预测方法，预测误差主要集中在0～100 kN范围内，占有率达到了99.47%，平均误差为26.40 kN，表明该方法对空气制动力这一复杂变量具有良好的预测精度。

表1 试验1中基于FLNN的空气制动力预测误差分布情况Tab.1 Prediction error distribution of air braking force by the FLNN based method in the test 1

图5 试验1中基于FLNN的空气制动力预测效果Fig.5 Prediction result of air braking force by the FLNN based method of in the test 1

图6 试验1中基于FLNN的空气制动力预测误差Fig.6 Prediction errors of air braking force by the FLNN based method in the test 1

3.3 试验2

试验内容：在涿鹿到茶坞区间K178+214至K279+929段，完成1次空气制动。

该试验的空气制动力预测效果和预测误差分别如图7和图8所示。对图中数据进行分析，预测误差区间分配如表2所示。由数据分析可知，FLNN的预测精度较高，预测误差在0～100 kN区间的占有率达到99.00%，空气制动力的平均预测误差为28.94 kN，满足工程精度需求。

图7 试验2中基于FLNN的空气制动力预测效果Fig.7 Prediction result of air braking force by the FLNN based method in the test 2

图8 试验2中基于FLNN的空气制动力预测误差Fig.8 Prediction errors of air braking force by the FLNN based method in the test 2

表2 试验2中基于FLNN的空气制动力预测误差分布情况Tab.2 Prediction error distribution of air braking force by the FLNN based method in the test 2

3.4 试验3

试验内容：在涿鹿到茶坞区间K279+929至K319+405段，连续3次空气制动。

该试验的空气制动力预测效果和预测误差分别如图9和图10所示。对图中数据进行分析，预测误差区间分配如表3所示。由数据分析可知，FLNN的预测精度较高，预测误差主要集中在0～100 kN，平均误差为24.86 kN，具有良好的预测精度，为工程化应用提供基础。

表3 试验3中基于FLNN的空气制动力预测误差分布情况Tab.3 Prediction error distribution of air braking force by the method based on FLNN in the test 3

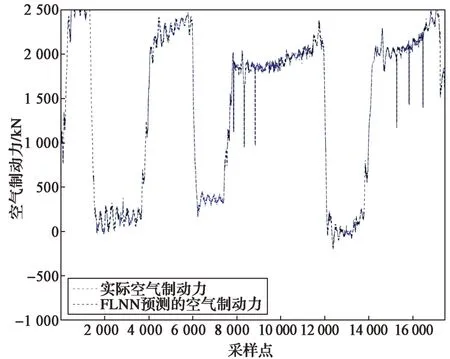
图9 试验3中基于FLNN的空气制动力预测效果Fig.9 Prediction result of air braking force by the FLNN based method in the test 3

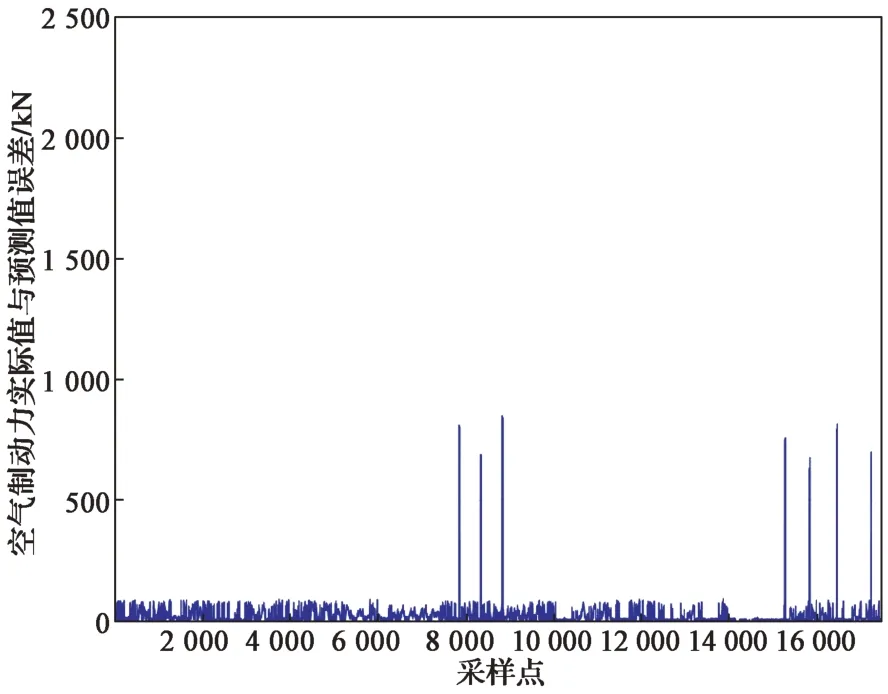
图10 试验3中基于FLNN的空气制动力预测误差Fig.10 Prediction errors of air braking force by the method based on FLNN in the test 3

4 结语

针对重载列车循环空气制动时空气制动力难以被预测的问题，本文提出了一种基于FLNN的空气制动力预测方法。首先，其采用RBF-NN网络训练空气制动离线数据，得到模糊逻辑形式的空气制动力离线预测规则；然后，计算当前数据与空气制动力离线预测规则的匹配度，得到相应的预测规则，输出空气制动力预测值。在大秦铁路进行试验，结果表明，本文提出的方法对重载列车在循环空气制动下的空气制动力强弱的预测精度具有较好的提升，对不超过100 kN的空气制动力的预测精确度达到了99%，平均误差为25 kN左右，对于循环空气制动操纵控制具有实际意义与应用价值。为了提高该方法对空气制动特性预测的精确度，后续将对该方法中数据集和特征变量的选择进行研究以获得最优的训练样本，并对非线性、不同过程的实际空气制动力的辨识进行精确分段研究。