钻孔瓦斯抽采效果影响因素的响应面分析

龚选平，薛 生，韩柏青，年福田，郑春山，成小雨

（1.中煤能源研究院有限责任公司，陕西 西安 710054；2.合肥综合性国家科学中心能源研究院（安徽省能源实验室），安徽 合肥 230031；3.安徽理工大学 安全科学与工程学院，安徽 淮南 232001；4.中煤新集能源股份有限公司，安徽 淮南 232000；5.中煤新集刘庄矿业有限公司，安徽 阜阳 236200）

2021 年煤炭在我国能源消费总量中占比56.0%，与往年相比，煤炭的生产和消费比重虽有所降低，但其在我国能源结构中仍然占据着主导地位，对我国未来的经济发展仍将发挥重要的作用[1-2]。随着我国煤矿开采深度的增加，地质条件日趋复杂，煤矿灾害事故的发生几率也在增加[3]。与其他煤矿事故相比，瓦斯事故一直是煤矿井下危险程度最大、死亡比例最高的事故类型之一[4]，对于瓦斯事故的遏制不容轻视。我国一直坚持“可保尽保、应抽尽抽、先抽后采、煤气共采”的瓦斯治理原则，瓦斯抽采是预防瓦斯事故的重要方法之一，而瓦斯抽采效果受到众多因素的影响。

郭欣等[5]以瓦斯渗流理论为基础，利用COMSOL Multiphysics 数值模拟软件建立考虑煤岩变形控制方程的气固耦合数学模型，研究相关因素对瓦斯有效抽采半径大小的影响；徐刚等[6]以流固耦合原理为基础，构建煤层瓦斯抽采流固耦合数学模型，借助FLUENT 数值模拟软件对煤层瓦斯预抽钻孔有效抽采半径进行数值模拟研究，对建新煤矿4207 工作面煤层瓦斯预抽钻孔布孔参数进行了优化；陈月霞等[7]采用三维数值模拟方法，研究分析了单排不同数量钻孔抽采条件下，煤层瓦斯压力及有效抽采区域的空间分布特征；张天军等[8]将相似模拟试验和数值模拟相结合，分析了负压变化对煤体瓦斯渗流特性的影响；江明泉等[9]运用数值模拟方法，探讨了无断层影响下顺层钻孔有效抽采半径变化规律；李守瑞等[10]提出了理论计算先做预测、数值模拟验证理论计算结果并指导开展现场抽采半径考察的综合方法，解决艾维尔沟矿区瓦斯抽采钻孔抽采半径考察精度不高的问题；刘殿平等[11]提出了以抽采钻孔瓦斯流量负指数衰减规律为基础、以工作面抽采达标指标为判据的有效抽采半径测定方法，推导出了以抽采率表示的钻孔有效抽采半径计算公式；Kong Xiangguo 等[12]通过构建流固耦合渗透率数值模型，分析水力冲孔条件下多因素对钻孔有效抽采半径的影响；Fang Huihuang 等[13]模拟分析多种因素对钻孔抽采效果以及有效抽采半径的影响，并对钻孔抽采条件下的多场多相耦合机理进行了探究。

国内外学者在瓦斯抽采效果的敏感性分析方面取得了丰硕的成果[14-16]，但以往研究多偏向于单一因素对瓦斯抽采效果影响的定性分析，而多因素交互作用下的瓦斯抽采效果变化规律需要进一步的定量分析。为此，以中煤新集公司刘庄矿为研究依托矿井，采用套孔应力解除法进行矿区地应力测试，基于煤体基质裂隙系统瓦斯解吸-扩散-渗流模型和COMSOLMultiphysics 数值模拟软件，分析钻孔瓦斯抽采过程，并利用Mintab 软件设计响应曲面试验，研究多因素交互作用对钻孔瓦斯抽采效果的影响，找出主次影响因素，确定钻孔有效抽采半径与多因素之间的关系式。研究结果对煤矿井下瓦斯抽采设计具有重要的参考价值。

1 地应力测试

渗透率是影响煤层瓦斯抽采过程的重要因素，而渗透率与地应力的大小密切相关，在研究矿区开展地应力实测试验，为数值模型构建提供地应力数据。现场测试采用套孔应力解除法，为保证测试数据准确可靠，在测点处布置了2 个地应力测孔K1和K2，测孔均布置在巷道南帮，测孔距离底板约1.5 m，两孔间距约1.2 m。

由于地应力测量过程中取得的岩心较为破碎，难以通过围压试验获取用于地应力计算的岩石力学性质参数，因此将现场从K1 孔和K2 孔取得的能够用于室内岩石力学试验的岩块加工成标准岩样（φ50 mm×100 mm），在中国科学院武汉岩土力学研究所研发的RMT-150C 岩石力学试验机上进行单轴压缩试验，以获取岩石的弹性模量、泊松比以及强度参数，K1 孔和K2 孔取得岩心的单轴压缩试验结果见表1。

表1 K1 孔和K2 孔取得岩心的单轴压缩试验结果Table 1 Uniaxial compression test results of cores obtained from boreholes K1 and K2

基于套心应力解除法的计算公式，以及测量得到的岩石力学参数，计算得到的测点的三维地应力测量结果如图1。

图1 三维地应力测量结果图Fig.1 3D in-situ stress measurement results

K1、K2 孔的套孔应力解除法地应力测试结果表明：现场测点的最大主应力、中间主应力的量值区间分别为18.92～19.80 MPa、14.52～14.57 MPa，最小主应力的量值为11.75 MPa；方位角分别为265.9°～266.4°、74.6°～88.6°、176.2～176.5.6°；倾斜角分别为7.0°～11.9°、78.1°～84.6°、-0.43°～-4.44°。水平应力大于自重应力，最大水平主应力与自重应力比的范围为1.38～1.41，说明测点处的应力以构造应力为主。

2 数值模型

2.1 煤体瓦斯运移模型

为了有效开展数值模拟研究，在理论上，首先构建数值模型的瓦斯运移控制方程，煤层中的裂隙将煤体分割为一个个基质单元体，煤基质中的吸附瓦斯在解吸后扩散到裂隙中，然后以渗流的方式在裂隙中流动，即为双重孔隙介质瓦斯运移模型。运用此模型时，需将基质渗透率定义为常数，仅考虑裂隙渗透率的动态变化，将煤层中的瓦斯运移简化为串联过程。

在煤层瓦斯抽采过程中，煤基质单元体内吸附瓦斯作为质量源向外解吸，使得扩散和渗流持续进行，煤基质与裂隙系统的质量交换方程为[17-18]：

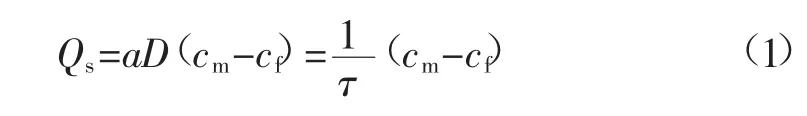
式中：Qs为单位体积煤基质同裂隙系统的质量交换率，kg/（m3·s）；a 为煤基质形状因子，m-2；D 为瓦斯扩散系数，m2/s；cm为煤体基质中的瓦斯含量，kg/m3；cf为煤体裂隙中的瓦斯含量，kg/m3；τ 为吸附时间，s。

根据理想气体状态方程，煤体基质与裂隙中瓦斯含量与压力之间的关系如下：

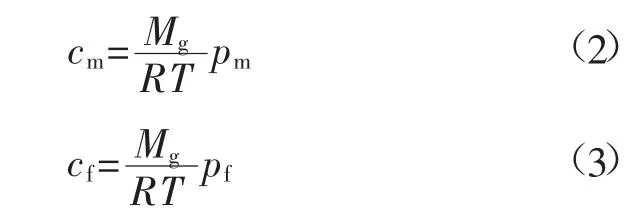
式中：Mg为气体分子质量，kg/mol；R 为普适气体常数，其值为8.314 J/（mol·K）；T 为煤层温度，K；pm为煤体基质中的瓦斯压力，MPa；pf为煤体裂隙中的瓦斯压力，MPa。

关于吸附时间τ 的基质内瓦斯向裂隙扩散方程可变为：

在煤层瓦斯抽采过程中，基质系统是裂隙系统的正质量源，裂隙系统是基质系统的负质量源，固由质量守恒定律可知，煤基质与裂隙系统的质量交换率应等于煤基质内瓦斯质量随时间的变化量，即：

式中：mm为单位体积煤体基质中总的瓦斯赋存质量，kg；t 为时间，s。

瓦斯的吸附作用只发生在煤基质中，煤基质中的瓦斯气体质量包含了吸附态瓦斯和游离态瓦斯，因此单位体积煤基质内的瓦斯赋存质量可以表示为[19]：

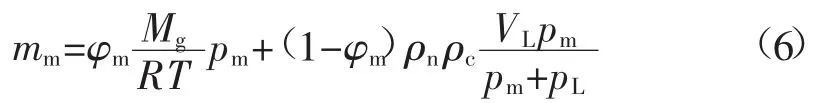
式中：φm为煤体基质孔隙度，%；ρn为标准状态下 的 瓦 斯 密 度，kg/m3；ρc为 煤 体 假 密 度，kg/m3；VL为Langmuir 体 积 常 数，m3/t；pL为Langmuir 压 力 常数，MPa。

其中瓦斯气体在标准状态时的密度可通过（7）式计算：

式中：Vm为标准状态下的理想气体摩尔体积，m3/mol。

整理可得煤基质瓦斯压力随时间变化的控制方程为：

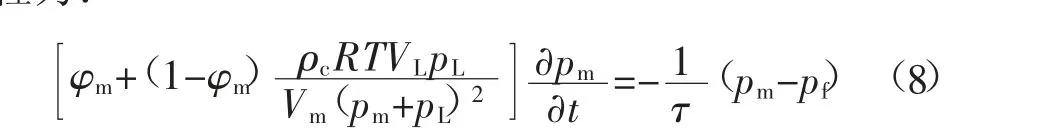
由此单位体积煤体裂隙系统内瓦斯质量平衡方程为：

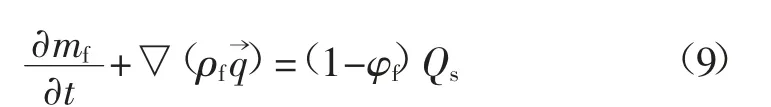
式中：mf为单位体积煤体裂隙中的游离瓦斯质量，kg；ρf为煤体裂隙系统中的瓦斯密度，kg/m3；q→为Darcy 定律 的速度矢量，m/s；φf为煤 体裂隙孔隙度，%。

单位体积煤体裂隙中赋存的游离瓦斯质量为：

由于瓦斯气体质量很小，忽略重力对瓦斯在煤层中扩散和流动的影响，根据Darcy 定律可得到气体的速度矢量为：

式中：k 为煤体渗透率，m2；μ 为瓦斯的动力黏度系数，Pa·s。

最后可得裂隙系统中的瓦斯流动控制方程：

该模型被用于控制瓦斯抽采数值模拟中的瓦斯流动过程，保证瓦斯抽采参数敏感性分析的准确性。

2.2 几何模型与边界条件

基于刘庄矿的实际地质条件，建立数值模型，该模型的长度为40 m，高度为10 m，钻孔之间的距离为10 m。边界条件方面，在模型两侧设置辊支撑，模型的底部边界设置固定约束，模型整体可以发生沉降。根据收集的矿井煤层参数资料，模型上表面施加均布载荷压应力19.8 MPa，煤层的初始瓦斯压力为0.6 MPa，煤层的孔隙度为0.01，瓦斯密度为0.716 kg/m3，瓦斯动力黏度为1.8×10-5Pa·s。数值模型示意图如图2。

图2 数值模型示意图Fig.2 Schematic diagram of numerical model

3 数值模拟

3.1 影响因素筛选

刘庄矿8 煤层150804 工作面的煤层瓦斯压力为0.6 MPa，不能以瓦斯压力下降到0.74 MPa 以下作为有效抽采半径的指标，根据相对压力指标法，如果煤层预抽率为30%，煤层的瓦斯压力下降量需达到51%[20]。当模拟煤层某点的瓦斯压力降至0.294 MPa 时，即该点瓦斯压力的下降量为51%，该点瓦斯抽采达标，则该点至钻孔处的距离即为有效抽采半径。

在多变量正交试验法中，通常结合极差分析探究正交试验结果的影响，极差分析可直观地依次得出各因素对试验数据影响的强弱程度。采用正交试验设计，开展钻孔瓦斯抽采参数对抽采效果的影响程度分析，筛选出影响最不显著的因素。以钻孔有效抽采半径R 为响应指标，研究抽采时间、煤层初始渗透率、抽采负压、孔径等参数对钻孔有效抽采半径的影响。以上4 种因子均设置3 个水平，采用3 水平4 因子的正交水平设计表，正交方案为L9（34），共9 种试验方案，正交试验方案见表2。

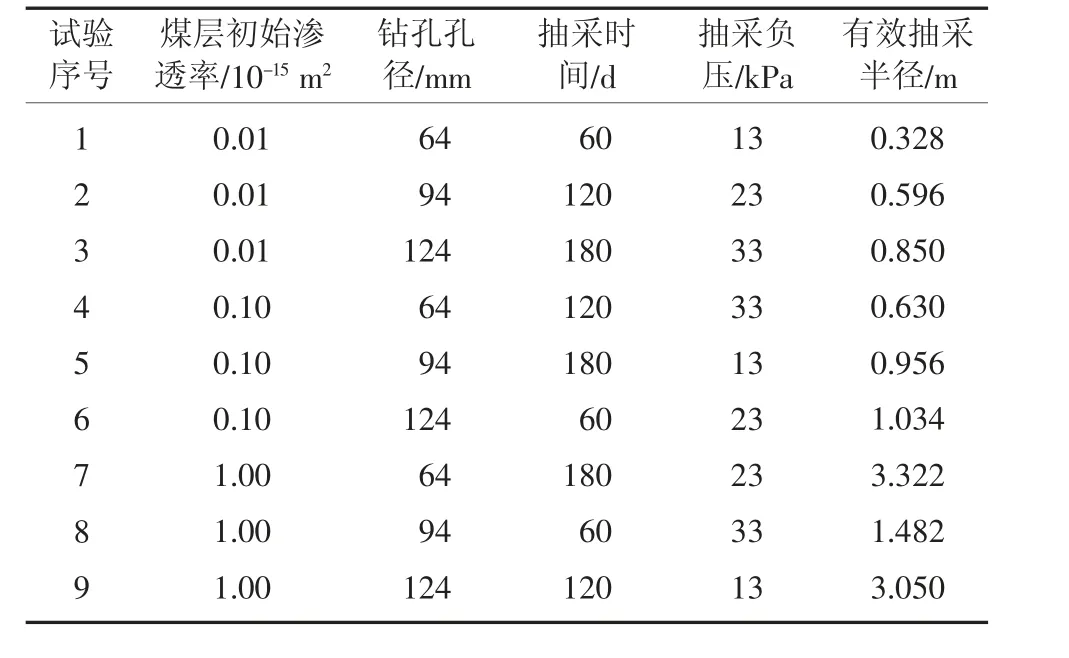
表2 正交试验方案Table 2 Orthogonal test schemes

对正交试验的结果进行处理分析，计算各因子各个水平的均值和极差，并进行归一化处理，再对各个因子进行排秩，了解各个因子对指标的影响程度。有效抽采半径极差分析见表3。不同因素不同水平下的有效抽采半径均值如图3。

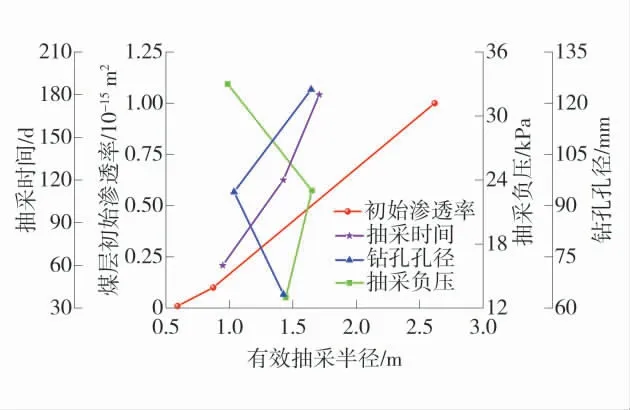
图3 不同因素不同水平下的有效抽采半径均值Fig.3 The mean values of effective extraction radius under different factors and their different levels

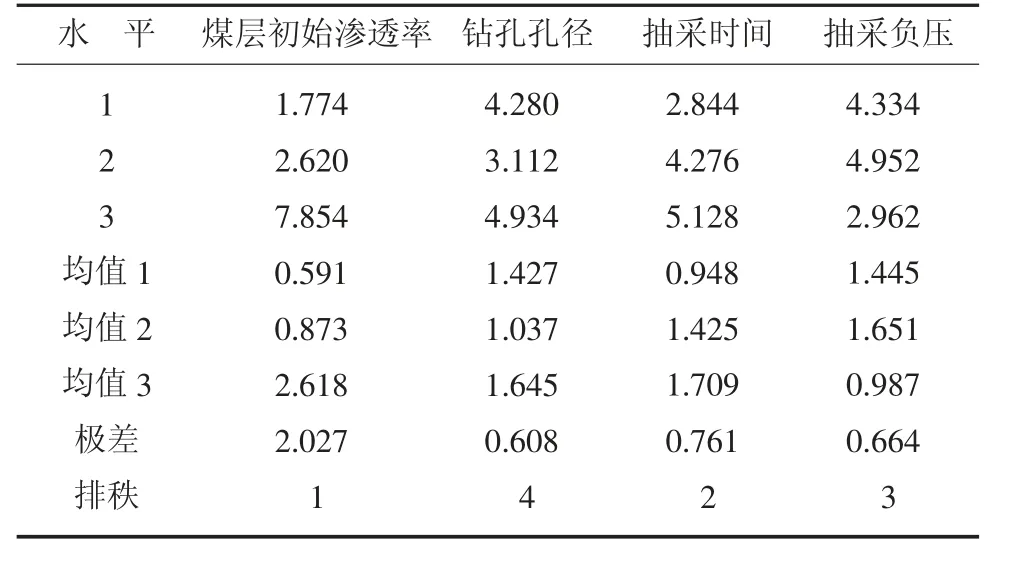
表3 有效抽采半径极差分析Table 3 Range analysis of effective drainage radius

由图3 可以看出，煤层初始渗透率这一因素在3 个水平下的均值差距最大，这表明其影响程度最大；钻孔孔径这一因素在3 个水平下的均值差不多，这表明其影响程度很小。另外，结合表3 可以得出，4 个因素对钻孔的有效抽采半径有着不同程度的影响，各因素的影响程度按照从大到小的排序为：煤层初始渗透率、抽采时间、抽采负压、钻孔孔径。其中，煤层初始渗透率这一因素的3 个水平中，钻孔有效抽采半径最大均值为2.618 m，最小均值为0.591 m，煤层初始渗透率的有效抽采半径极差为2.027 m，说明其对钻孔有效抽采半径的影响程度最高；钻孔孔径这一因素的3 个水平中，钻孔有效抽采半径最大均值为1.645 m，最小均值为1.037 m，钻孔孔径的有效抽采半径极差为0.608 m，说明其对钻孔有效抽采半径的影响程度最低。因此，在响应曲面试验中剔除钻孔孔径这一因素，着重分析煤层初始渗透率、抽采时间和抽采负压对钻孔瓦斯抽采效果的影响。

3.2 响应曲面模型

响应曲面法是利用数学和统计分析进行参数优化的方法，通过拟合响应函数与影响因素之间的一阶或者二阶模型作为真实响应函数的1 个近似，在多元线性回归的基础上主动收集数据，以获得具有较好性质的回归方程。建立的复杂多维空间曲面较接近实际情况，所需要的试验组数相对较少。响应曲面法经常使用的设计方法为中心复合设计和Box-Behnken 试验设计。在因素相同时，Box-Behnken 试验设计比中心复合设计试验次数少，而且具有近似旋转性、无序惯性，没有试验因素同时为高水平的试验组合，因此采用Box-Behnken 试验设计。Box-Behnken 试验设计共15 种试验方案，运用COMSOL软件解算不同抽采参数条件下的钻孔有效抽采半径。响应曲面试验设计方案及结果见表4。

根据结果可建立有效抽采半径与多因素的耦合关系模型，协助指导抽采参数动态优化调整。由于采用大于二阶多项式的响应曲面模型会使得高次项系数的数目增大，大大增加计算量，若采用二次多项式，较为灵活简单，且拟合精度较高，应用广泛，因此采用二次多项式来表达。针对表4 中得到的模拟结果，采用响应曲面试验开展多因素回归拟合分析，建立有效抽采半径与多因素之间的多项式响应曲面回归方程，如下式：

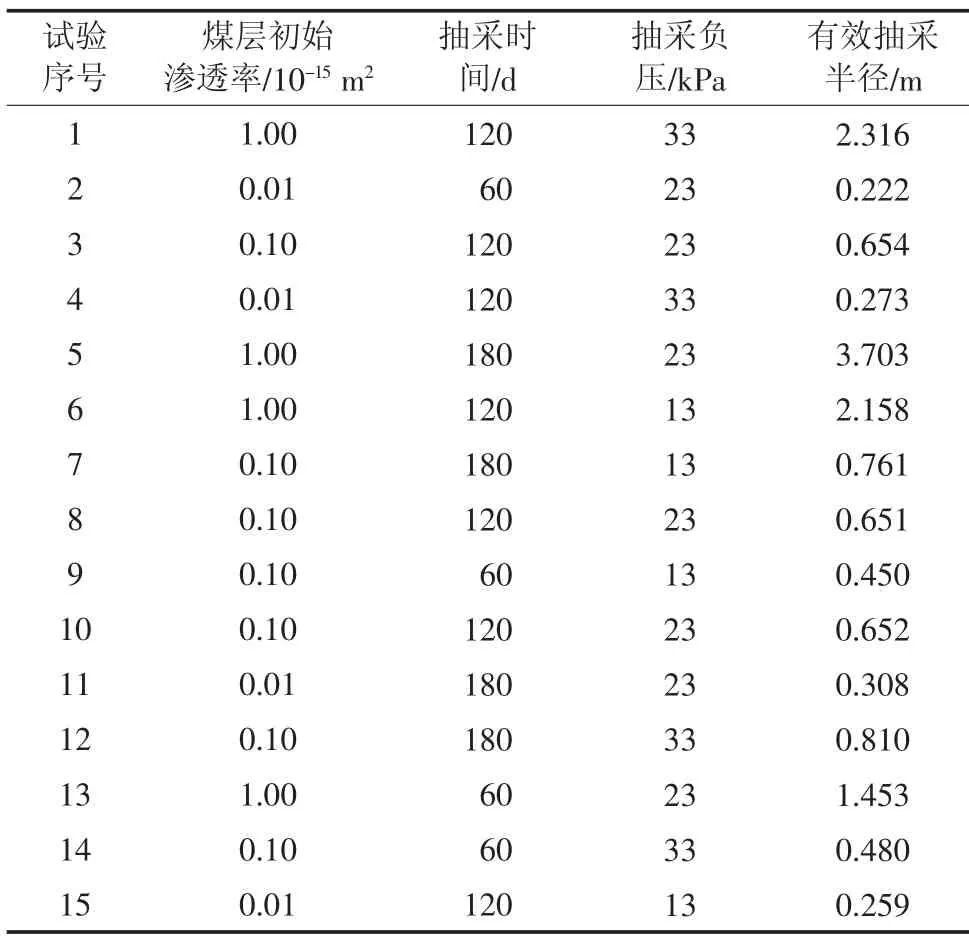
表4 响应曲面试验设计方案及结果Table 4 Response surface experimental design schemes and results

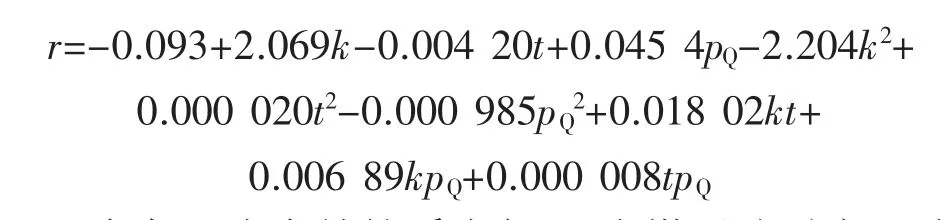
式中：r 为有效抽采半径；k 为煤层渗透率；t 为抽采时间；pQ为抽采负压。

3.3 有效抽采半径响应曲面

二次多项式响应面模型的近似函数可通过变量代换转化为形式上的线性函数，然后通过试验样本空间的参数矩阵得到基于响应面模型的函数值，由此计算响应值与实验值之间的误差，利用最小二乘法求解上式中二次多项式系数。方差分析见表5。表中P 值为各项显著性的关键分析值，如果P 值越小，说明极端的假设情况发生的概率越小，则说明结果越显著。

由表5 可以看出，目标函数R 的响应面模型P值远远小于0.01，即表示模型显著性极好，所得多项式回归方程可准确反映各因素对响应值（有效抽采半径）的影响。模型中的初始渗透率项、抽采时间项、初始渗透率的平方项以及初始渗透率与抽采时间交互项的P 值都小于0.05，说明这几项在模型中都是显著的，其他项的P 值都没远大于0.05，说明其它项的显著性也可以接受。其决定系数为0.9957，表明99.57%以上的响应值均可由这个模型解释。

表5 方差分析Table 5 Variance analysis

根据二次多项回归方程绘制出响应曲面，煤层初始渗透率与抽采时间的响应曲面如图4，煤层初始渗透率与抽采负压的响应曲面如图5，抽采时间与抽采负压的响应曲面如图6。

图4 煤层初始渗透率与抽采时间的响应曲面Fig.4 Response surface of initial permeability of coal seam and extraction time

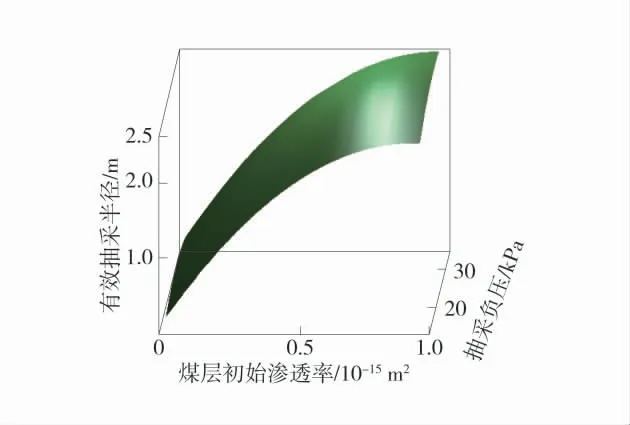
图5 煤层初始渗透率与抽采负压的响应曲面Fig.5 Response surface of initial permeability of coal seam and negative drainage pressure

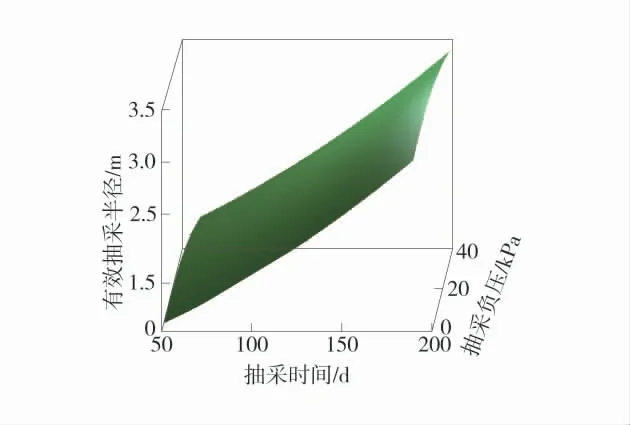
图6 抽采时间与抽采负压的响应曲面Fig.6 Response surface of drainage time and drainage negative pressure

煤层初始渗透率、抽采时间与抽采负压两两之间的响应曲面图表明，在煤层初始渗透率的坐标轴方向上，钻孔的有效抽采半径变化最快，而在抽采负压的坐标轴方向上，钻孔有效抽采半径变化最慢。其中，图4 的响应曲面扭曲最大，说明煤层初始渗透率与抽采时间之间的交互作用显著；图5 的响应曲面有一些扭曲，说明煤层初始渗透率与抽采负压之间的交互作用有些许显著；图6 的响应面没有明显的扭曲，说明两者的交互作用不显著。这也证实了煤层初始渗透率在钻孔抽采瓦斯过程中，对钻孔的有效抽采半径影响显著性极大；抽采时间对钻孔的有效抽采半径影响显著性较大；抽采负压对钻孔的有效抽采半径影响显著性较小。因为影响钻孔瓦斯抽采最为重要的因素是煤层的渗透率，当煤层渗透率高时，煤层中的裂隙发育好，透气性高，瓦斯更容易在煤层中流动，也更容易被钻孔抽采出来。综上所述，对钻孔有效抽采半径的影响程度为：煤层初始渗透率＞抽采时间＞抽采负压，这与正交试验的极差分析结果相互吻合。故对于低透气性煤层，在抽采前采取水力割缝、保护层开采、松动爆破等卸压增透措施极为重要，可增加低透气性煤层的渗透率，提高瓦斯抽采效率。

4 结 语

1）根据正交试验结果，煤层初始渗透率对应的有效抽采半径极差最大，可达2.027 m；钻孔孔径对应的有效抽采半径极差最小，其值为0.608 m。煤层初始渗透率对钻孔有效抽采半径的影响程度最大，抽采时间、抽采负压、钻孔孔径的影响程度依次减小。

2）采用响应面法得到煤层初始渗透率k、抽采时间t、抽采负压pQ与有效抽采半径r 的关系模型为r=-0.093+2.069k-0.004 20t+0.045 4pQ-2.204k2+0.000 020t2-0.000 985pQ2+0.018 02kt+0.006 89kpQ+0.000 008tpQ，该响应面模型P 值小于0.05，表明其具有较好的显著性，模型决定系数为0.995 7，该模型可以解释99.57%以上的响应值。

3）多因素交互作用对钻孔有效抽采半径变化产生新影响，煤层初始渗透率的影响仍然最显著，同时，煤层初始渗透率与抽采时间的响应曲面扭曲程度最大，二者之间对抽采半径的交互影响作用也最大；抽采时间与抽采负压的响应曲面扭曲程度最小，说明二者的交互影响作用不显著。故提高煤体渗透率是瓦斯抽采提效的主要途径之一。