基于测井资料与优化通用向量机的煤层气含量预测模型

陈 涛，丁海琨，张占松，郭建宏，谭辰阳，周雪晴，朱林奇

（1.长江大学 油气资源与勘探技术教育部重点实验室，湖北 武汉 430100；2.长江大学 地球物理与石油资源学院，湖北 武汉 430100；3.中国石油测井公司国际合作处，陕西 西安 710077；4.中国科学院深海科学与工程研究所，海南 三亚 572000）

煤层含气量是煤储层评价研究的关键参数之一，是煤层产能评价、生产布局及资源挖潜的关键所在。而煤层含气量受成藏地质构造、地质水文特征、煤变程度、煤质工业组分、煤层有效埋深和净厚度、储层压力及渗透率、煤层顶底板岩性及厚度等众多因素的影响[1-3]，是众多因素耦合作用的产物。目前，对煤储层含气量的定量评价大致可分为数值模拟[4-7]、基于测井参数[8-11]和实验组分[12-14]及地震属性[15-16]的单参变量或多参变量线性回归预测法、参数井绳索取心现场解吸测试和人工智能4 大类。然而，参数井绳索取心法费用成本高难以实现；线性回归法对于非均质性极强的煤储层难以实现高精度评价；由于三相态含气量数值模拟技术亟待突破，数值模拟很难实现生产精细评价。近年来，基于机器学习和深度学习的方法越来越多地应用到非均质性极强的非常规储层参数评价中，用于挖掘数据隐藏的非线性关系，如循环神经网络、BP 神经网络、SVM 神经网络、决策树、长短期记忆网络及融合智能算法等[17-21]，研究表明，这些技术的引入对煤层含气量预测的可信度及可靠性较好。然而，BP 神经网络对样本量有一定要求，且受参数影响大，导致训练复杂性大，局限性明显；随机森林抗干扰能力较强，在处理特征遗失及不均衡数据时泛化性好，但对超出训练集数据邻域的样本会出现预测盲区，很可能使在进行建模时某些高频噪声的样本出现过拟合影响模型泛化性；支持向量机无需复杂的拓扑结构，对小样本适应强，具有很强的鲁棒性，但受噪声样本影响较大。而采用通用向量机[22]（GVM）算法作为核心建模技术，很大程度上平衡了上述问题；有研究表明：在少量训练样本甚至缺失训练样本的情况下，训练出来的回归模型仍然具有良好的鲁棒性和泛化性[22-23]。为此，基于煤层含气量测井响应相关性结合地球物理理论进行曲线重构，再通过对Elastic Net 方法添加正则化项施加惩罚来选取敏感特征变量，解决多重共线性问题和冗余参数；提出用改进的量子粒子群优化算法（IQPSO）对GVM 模型关键参数进行寻优，最优化处理建模的每个关键环节进而使模型整体性能提升，以此构建泛化性好、强鲁棒性的煤层含气量高精度预测模型，并用实际区块数据验证方法的适应性和有效性。

1 煤层含气性测井响应分析

1.1 数据来源

研究数据来自华北沁水煤田东南部柿庄南区块3 号煤层，是目前勘探开发的热点地区。由于受地质构造、聚煤沉积环境、水文地质条件、煤层气成因及来源的差异性响应，储层平面非均质性极强，含气量测井响应特征复杂，高精度评价难度大[24]。样品源于勘探区12 口关键井280 组有效煤心样品深度部分。样品含气量及常规测井响应数据（部分）见表1。

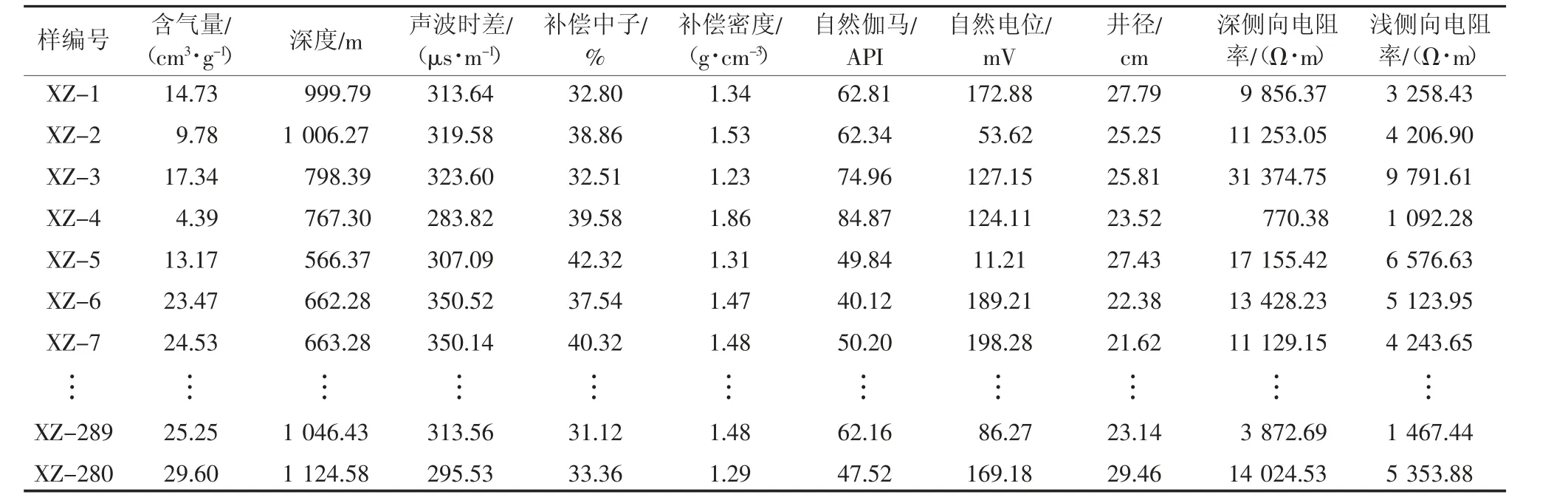
表1 样品含气量及常规测井响应数据（部分）Table 1 CBM content of samples and conventional logging data（part）

1.2 含气量与测井参数之间相关性分析

研究表明，煤层含气量与有机质和无机质2 种单一组分的相对丰度存在函数关系，有机质含量在某一特定地区保持相对稳定，而无机组分在区块内会发生显著的横向和纵向变化，并表现为测井响应的差异性。测井的纵向分辨率相对较高，不同储层蕴含复杂的地质储层信息，煤层含气量响应具有特殊性及复杂性。煤层含气量与测井参数交会图如图1。

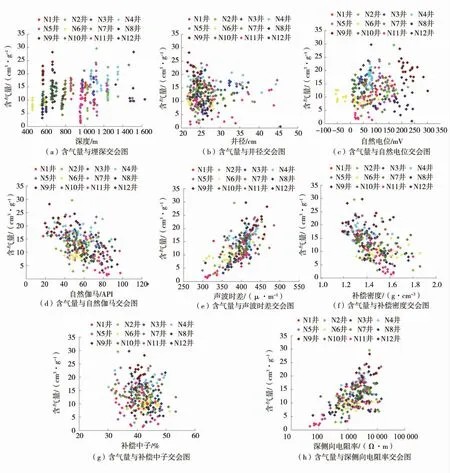
图1 煤层含气量与测井参数交会图Fig.1 Cross plot of coal seam gas content and logging parameters

煤层含气量根本影响因素是煤变程度。理论上，煤层埋深一定程度上影响烃热分解能力，同时很大程度上决定了煤层气的封堵条件，浅煤层含气量随埋深增加而升高，当埋深达到某一临界深度后，受地质构造、后期的封闭条件及聚煤沉积环境等影响含气量解吸缓慢甚至出现降低趋势，可见煤岩埋深对含气量评价是受研究区地质因素影响较大的不稳定变量。井径曲线主要反映地层的脆性指数及机械强度，与煤岩类型紧密相关，煤层含气后对煤岩类型影响甚微，即含气量对井径曲线敏感性较弱。煤岩是电阻率较高的非导电介质，扩散和吸附作用产生自然电位，其本身与含气量敏感性较弱，但自然电位异常幅度很大程度上取决于黏土含量、泥浆滤液及煤岩厚度等影响，一定程度上表现为含气量的差异性。煤岩骨架自身放射性较低，其放射性取决于成煤过程吸附的黏土矿物等外来矿物，一方面黏土矿物含量越高，对应煤岩有效孔隙空间就越少，含气量就越低，同时黏土吸附削弱了煤岩的吸附能力，降低了其比表面积，致使煤层含气量一定程度上降低。声波时差可反映煤岩的抗压强度和致密程度，含气后声波能量严重衰减，表现为声波时差明显增大甚至出现“周波跳跃”现象，声波时差对含气量较敏感。煤本身基质密度较低，理论上其密度响应值与煤层致密程度紧密相关，煤层越致密其孔隙空间越小，含气量也就越小，实际上受扩径及黏土含量影响单井表现往往并不是这样，甚至出现相反的的趋势。补偿中子反映煤储层的含氢指数，理论上含气量越高中子测井值衰减越剧烈，补偿中子越小，但受扩径、泥饼、泥质及炭质夹矸等一系列因素影响较大，单井有时表现并不明显。煤层电阻率很大，但电阻率响应值还受煤岩厚度、井眼尺寸、泥浆侵入、孔隙填充及夹矸等较多因素影响，研究区总体上煤层含气量与深侧向电阻率呈正相关。

综上分析，研究区煤储层双重孔隙结构、强储层非均质性导致煤层含气量与测井参数响应极为复杂，为充分挖掘测井响应特征蕴含的储层信息，提高含气量评价精度，根据测井原理结合其对含气性的响应特征分析，计算了9 个衍生参数，分别为复合参数M 和N、三孔隙度差比值C 和B、自然电位幅度差值△SP、双电阻率差比值△lg（R）和Ra 及双电阻率对数值lg（RD）和lg（RS），计算公式为：

式中：GR 为自然伽马，API；DEN 为补偿密度，g/cm3；RD 为深侧向电阻率，Ω·m；AC 为声波时差，μs/m；CNL 为补偿中子，%；SP 为自然电位，mV；SSP为静自然电位，一般取泥岩基线值，mV；RS 为浅侧向电阻率，Ω·m。

计算含气量及测井以及其衍生参数之间的Pearson 相关系数，但Pearson 相关系数往往偏重于线性相关程度而忽略了含气量与测井参数之间的非线性关系。含气量与测井及其衍生参数相关性热图如图2。由图2 可知，各测井参数之间存在多重共线性，会降低模型稳定性，且冗余信息很大程度上给模型带来噪声干扰，难以进行含气量高精度评价，因此特征变量的选取非常有必要。

图2 含气量与测井及其衍生参数相关性热图Fig.2 Heat diagram of correlation between gas content and conventional logging parameters

2 建模方法理论

为充分挖掘储层信息并解决多重共线性问题，研究引入适合GVM 神经网络建模的Elastic Net 分析方法优选建模特征变量，并针对GVM 模型参数进行优化建立稳健的含气量预测模型。

2.1 Elastic Net 特征变量选择

弹性网络（Elastic Net，EN）是2005 年由ZouH[25]等在研究岭回归（RR）和拉索回归（LASSO）理论基础上提出的一种新鲁棒正则化方法。式（8）为ElasticNet 方法代价函数惩罚项，其将拉索回归和岭回归惩罚项加权组合。该方法继承LASSO 回归的稀疏性的同时很好地解决了共线性问题。Elastic Net 方法被证实具备很好群组效应和稀疏性，对异常值及重尾误差具有很好的鲁棒性，尤其适用于小样本数据变量筛选。

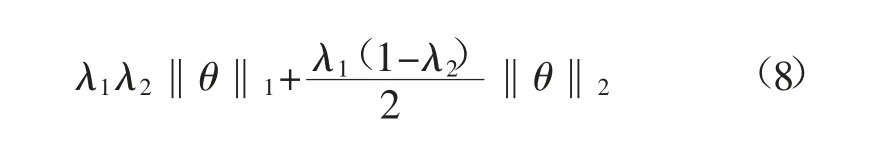
式中：λ1为惩罚项相对于拟合错误的重要程度，大于0；λ2为2 种范数正则化的比例，取0～1；‖θ‖1为L1正则化；‖θ‖2为L2正则化。

2.2 通用向量机（GVM）

通用向量机（GVM）模型是厦门大学赵鸿教授在2016 年基于蒙特卡罗（Monte Carlo，MC）算法提出来的一种机器学习新方法[22]。该模型结合BP 神经网络的经验风险最小化策略和支持向量机（SVM）的经验风险最小化策略，采用MC 算法调整模型权值直至获得最优模型。该模型被证实具有很好的泛化能力，对小样本具有良好的预测效果，且模型对单个样本的微小波动具有更强的鲁棒性，模型抗噪声干扰能力强。

GVM 模型主要超参数为隐含层节点数和敏感度控制参数β，通过将β 控制在一定范围内就可以使模型对输入向量的微小波动保持强鲁棒性，这样就可以用更多的隐藏层节点增强模型泛化能力的同时有效抑制过拟合。同时采用镜面对称思想固定输出权值矩阵W2，通过基于权值偏导数的蒙特卡罗（Derivative Monte Carlo，DMC）算法[23]来调整权值Wβ、W1和Wb，优化模型，减小式（9）代价函数使得模型整体逐步收敛到稳定最优解。

式中：COST 为代价函数；RMSE 为均方根误差；N 为样本个数。

2.3 改进的量子粒子群算法（IQPSO）

GVM 模型性能取决于权值向量、偏置向量及控制向量。蒙特卡罗算法优化GVM 网络参数采用单步变异方式，1 次仅优化1 个权值，且隐含层节点数同条件下一般来说至少10 倍于BP 神经网络，是以牺牲训练时长和模型收敛速度来增强模型的鲁棒性与稳定性。本质上来讲，优化GVM 模型网络参数就是搜索最优网络参数使得式（9）取得最小极值。PSO算法就是解决此类问题行之有效的经典方法。

PSO 算法是由Eberhart 等[26]于1995 年模拟鸟群觅食行为提出的一种全局最优化算法，因其简单可行、收敛快、稳健性好等优点被广泛应用于各领域最优化问题中。但该算法星环状结构信息交互方式导致搜索寻优过程中由于其种群多样性自进化消失快而过早收敛，在解决形如式（9）这种多局部极值问题中很难跳出局部最优。基于此，将量子比特系统引入粒子群算法，并根据代价函数动态调整比特量子旋转角和交叉变异概率对量子粒子群算法[27]（QPSO）进行改进提出一种新的量子粒子群算法，使得粒子以更大概率跳出局部最优同时兼顾泛化及求精能力。

综上，利用Elastic Net 方法优选建模特征变量，针对研究所用小样本不均衡数据选择具有优势的GVM 网络建立神经网络模型，考虑到GVM 模型存在的缺陷及粒子群算法（PSO）参数寻优对本研究适应性差，提出了改进的量子粒子群算法对决定模型性能的关键控制参数进行全局优化，通过此三者紧密联合构建高精度、强鲁棒性和稳定性的煤层含气量预测模型。

3 模型构建及性能分析

3.1 模型构建

3.1.1 特征参数选取

根据Elastic Net 方法，在进行变量筛选前对数据做标准化处理，消除特征参数间的差异性，避免因此导致特征丢失。由式（8）可知，EN 特征筛选2个核心参数为正则化参数λ1（λ1＞0）和权重调节系数λ2（0＜λ2＜1）。为获得最佳Elastic Net 参数，在python平台Elastic NetCV 模块中，先将数据随机等分为3组，网格搜索采用3 折交叉验证确定最佳权重调节系数为λ2=0.32，再根据均方差MSE 随不同惩罚系数的变化曲线基于最小MSE 准则确定正则化参数λ1。3 折交叉验证下不同正则化参数MSE 变化曲线（λ2=0.32）如图3，最佳正则化系数为λ1=0.58。

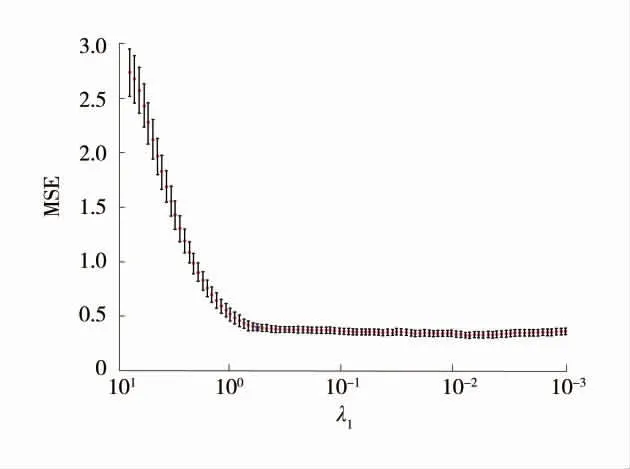
图3 3 折交叉验证下不同正则化参数MSE 变化曲线（λ2=0.32）Fig.3 MSE variation curves of different penalty coefficients under 3-fold cross validation（λ2=0.32）

基于所选最佳EN 方法系数（λ2=0.32，λ1=0.58），EN 方法通过最小角回归算法（Least Angle Regression, LAR）迭代计算19 个测井及其衍生参数稀疏系数[27]，将稀疏系数为0 的冗余变量滤除即为特征参数，该方法降维的同时很好地解决了多重共线性问题。特征参数贡献率如图4。

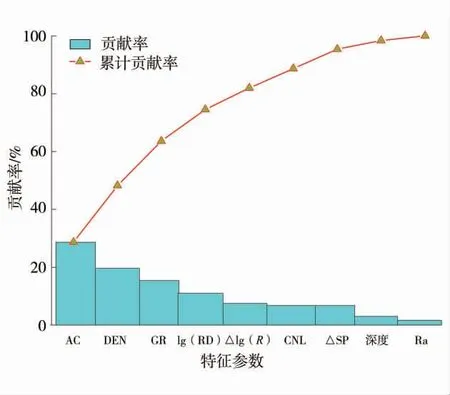
图4 特征参数贡献率Fig.4 Contribution rate of characteristic parameters

由图4 可知，AC、DEN、GR、lg（RD）、CNL、△lg（R）、△SP 7 个参数对模型精度总贡献率达到95.38%，因此选取这7 个参数作为GVM 模型的优选特征。

3.1.2 网络结构确定

在进行GVM 模型权值向量、偏置向量及控制向量寻优前首先要确定模型结构，即要确定隐藏层节点个数。隐藏层节点个数对模型性能的影响如图5，MAPE 为平均绝对百分比误差，表征模型偏差程度。随着隐藏层节点个数的增加，模型精度越来越好，模型训练时长开始缓慢增加，当隐藏层节点数超过105 时，模型性能反而下降，精度开始降低，且训练时长急剧增长。基于以上分析，隐藏层节点数为105。

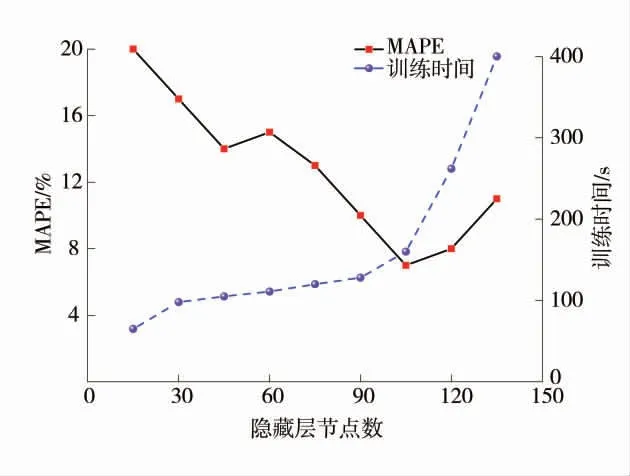
图5 隐藏层节点个数对模型性能的影响Fig.5 Contribution rate of characteristic parameters

一般来说，GVM 模型要求激活函数f 满足非线性、有界性和连续性。考虑一般情况，利用先验样本数据特征对GVM 模型常见3 种传递函数性能进行模拟对比，不同传递函数运算效率对比如图6。由图6 可知，对于特征空间3 种传递函数都具有可行性，相对而言tanh 函数运行效率高且对DMC 算法来说其参数变异区间较广，容错率较高。因此将tanh 函数作为GVM 模型的传递函数。

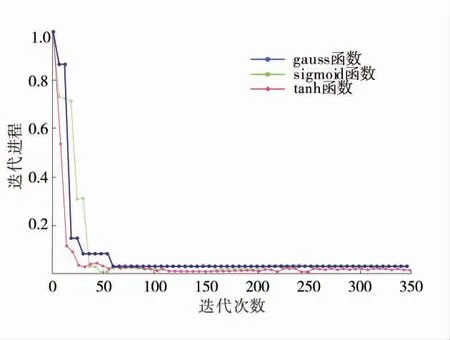
图6 不同传递函数运算效率对比Fig.6 Contribution rate of characteristic parameters

3.1.3 网络参数优化

利用IQPSO 算法优化GVM 网络参数，每个量子粒子代表1 组GVM 网络参数（Wβ、W1和Wb），将式（9）作为IQPSO 算法的适应度函数。GVM 参数寻优图如图7。

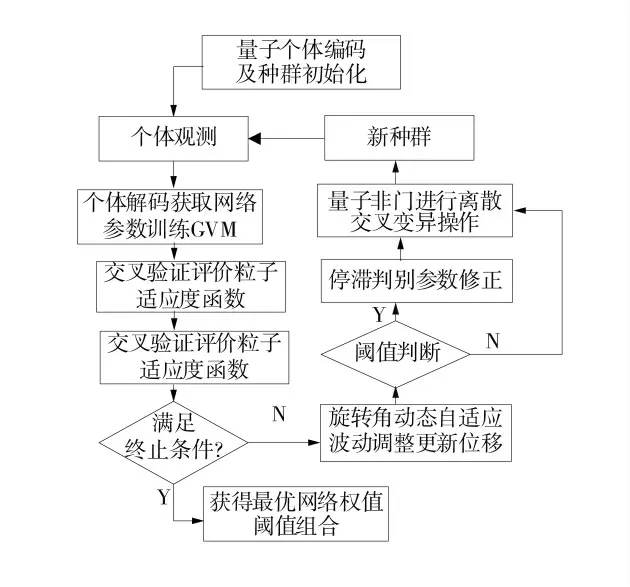
图7 GVM 参数寻优图Fig.7 GVM parameter optimization diagram

算法具体流程步骤如下：

步骤1：初始化。利用式（10）量子比特编码每个粒子qi，并初始化参数，IQPSO 初始化参数见表2。包括种群规模N，最大进化代数Imax，停滞判别参数ω，交叉验证误差判别阈值ε，量子门旋转角范围［θmin，θmax］，变异概率范围［pmmin，pmmax］。

表2 IQPSO 初始化参数Table 2 Initialization parameters of IQPSO

式中：［cosθij，sinθij］T为1 个量子比特；M 为量子比特空间维数；θ 为量子粒子相位。

步骤2：随机观测每个粒子生成二进制解并进行解空间转换。

步骤3：采用3 折交叉验证评价每个粒子适应度函数，保存全局最优解Pg＝（pg1，pg2，…，pgM）和当前每个粒子的局部最优解PL＝（pL1，pL2，…，pLM）。并判断交叉验证误差判别阈值ε 和最大进化代数Imax，若满足则进行步骤4，否则进行步骤6。

步骤4：采用二进制引力搜索算法[28]量子旋转门策略结合式（10）更新量子相位向量θi＝（θi1，θi2，…，θiM），进而更新个体位移。

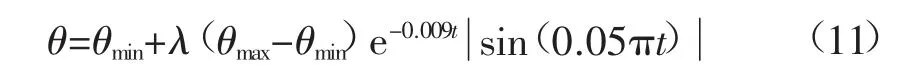
式中：λ 为控制θ 调整幅度的常量，经反复实验模拟取值e0.036效果最佳；t 为时间。

采用式（11）符合θ“粗中有细”的调整策略，有效提高模型性能同时平衡其泛化能力。

步骤5：停滞参数ω 判断，若满足则利用量子非门进行离散交叉变异操作更新进化种群使粒子以更大概率快速跳出局部极值。

步骤6：在IQPSO 算法优化基础上，执行GVM模型DMC 加速变异算法进一步提升模型全局寻优能力，直至达到算法停止条件输出最优解。

3.2 模型性能

为验证改进策略，基于上述优选的7 个特征测井参数分别用MC 算法、DMC 算法、PSO 寻优策略及本文方法优化GVM 网络参数建立煤层含气量预测模型。建模过程将280 组样本数据随机等分为4组，1 组作为测试集不参与建模验证模型泛化性，其余3 组进行3 折交叉验证用于确定模型参数。对建模集（训练集和验证集）和测试集进行测试对比，用3 次交叉验证平均均方根误差和拟合优度衡量模型整体性能，并对各模型进行测试对比，各算法适应度函数收敛曲线如图8。

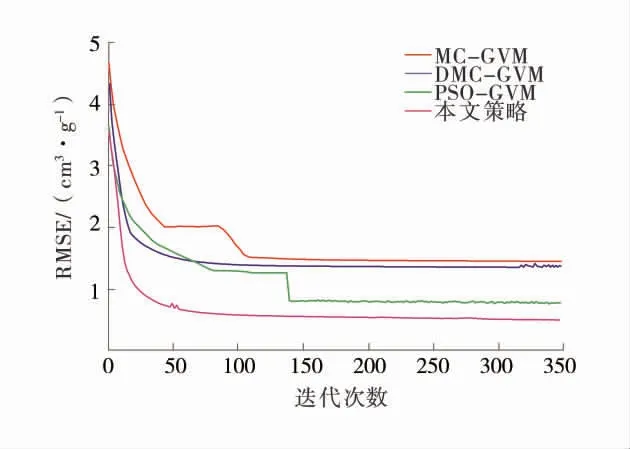
图8 各算法适应度函数收敛曲线Fig.8 Convergence curves of fitness function of each algorithm

由图8 可知，在其他条件相同的情况下，寻优策略其寻优能力优于其它3 种方法，而在收敛速度上DMC 算法是最快的。同时还可看出，MC 算法和DMC 算法尽管收敛速度稍快，但对于研究目标函数全局寻优能力较差，收敛精度稍差，PSO 算法尽管一定程度上增强了全局寻优能力，还是陷入了局部最优值。而寻优策略，虽多次早熟收敛，但随着迭代次数增加逐步收敛并在后收敛到全局最优达到不错的收敛精度。由此可见，结合IQPSO 和DMC 算法的GVM 网络参数寻优策略虽然在收敛速度上略有损失，但极大提升了模型精度。

通过拟合优度、均方根误差、平均绝对百分比误差和相对分析误差4 个指标，可以综合全面地评估模型性能。各评价模型的预测精度评价指标见表3。

由表3 结果可见，不论是训练集还是验证集，IQPSO 算法优化策略GVM 模型预测精度均优于其他3 种方法。可见采用的GVM 网络核心参数优化策略可有效改善模型性能，提高模型预测精度。同时测试集可以看出，训练得到的模型其测试集平均均方根误差为0.648，平均绝对百分比误差8.69%，相对分析误差3.23，相对其他3 种方法均有大大的提升，说明该算法泛化性强，能有效抑制过拟合。

表3 各评价模型的预测精度评价指标Table 3 Evaluation index of prediction precision of each model

GVM 模型集BP 神经网络模型和SVM 模型优点于一体，为验证模型对所研究问题的有效性及验证模型的鲁棒性，将本文模型、基于本文优化策略的7×9×1 结构的BP 神经网络模型和SVM 模型及传统多元回归法对研究区同一盲井3 号层进行含气量预测，A13 井3 号煤层含气量预测成果如图9。

图9 A13 井3 号煤层含气量预测成果Fig.9 Prediction results of 3# coalbed methane content in A13 well

由图9 可以看出，多元回归模型明显存在“高值偏低，低值偏高”的有偏现象，整体上均比神经网络含气量模型差，且多元回归法预测结果整体为1 条直线，并不符合煤层强非均质性的特点，因此不合理，参考价值不大；神经网络预测含气量整体上形态走势相近，一定程度上符合煤层强非均质性的特点，BP 神经网络含气量模型对样本量要求高且训练难度大，也存在有偏现象误差较大；796～797 m 为夹矸段，理论上含气量为低值，而支持向量机含气量模型表现为平稳直线且与正常响应段近乎持平，且796.6～797.6 m 存在明显扩径，尽管经过扩径校正，但仍无法消除曲线失真对含气量建模的影响。可以看出，支持向量机含气量模型抗井径失真能力明显不如通用向量机含气量模型和BP 神经网络含气量模型；在煤层上下测井响应半幅点突变段通用向量机含气量预测精度明显优于通用向量机模型和BP神经网络模型。综合盲井验证结果分析，提出的基于弹性神经网络测井参数优选和改进量子粒子群结合变异蒙特卡洛算法优化通用向量机模型效果最好，模型稳健性好、鲁棒性强，能满足该地区含气量高精度计算要求，为煤层气生产提供总体上有力支撑与指导，同时为煤层含气量高精度预测提供了新方法策略。

4 结 语

1）经过常规交会图和含气量相关性热图分析各测井及其衍生参数与煤层含气量相关性可知煤层含气量响应特征明显，不同测井参数的含气量响应差异较大，各测井参数间存在不同程度的多重共线性。

2）在煤层含气量预测建模过程中，引入弹性网络进行属性约简解决冗余信息对含气量建模精度的影响，真实定量化表征测井参数与煤层含气量间的非线性关系。从实际结果可知，该特征参数优选策略符合地球物理测井理论，是行之有效的去冗余化方法，提升了建模精度。

3）针对煤储层非均质性强且煤层含气量小样本不均衡特点引入通用向量机算法，通过试验调整并确定了最优的GVM 模型拓扑结构参数，然后使用改进的量子粒子群算法优化GVM 模型权值建立最终煤层含气量预测模型。将该模型与相同策略下的支持向量机、BP 神经网络及传统多元回归模型进行对比，建模效果优于其他方法，能有效满足勘探区含气量高精度要求及生产指导，可进行推广使用。