潜艇紧急倒车工况流场与水动力的大涡模拟研究
汪训铭,张 楠
(中国船舶科学研究中心,江苏无锡 214082)
0 引 言
在船舶水动力学领域,以螺旋桨的来流速度V与螺旋桨的旋转角速度ω来定义,可以将螺旋桨的工作模式分为正车前进(+V,+ω,第一象限)、后退正车(紧急正车)(-V,+ω,第二象限)、前进倒车(紧急倒车)(+V,-ω,第三象限)和倒车后退(-V,-ω,第四象限)四种工况[1]。螺旋桨正常运行时的常见工作模式为正车前进工况,该模式下螺旋桨在稳定转速下所产生的推力、转矩基本不随时间变化而变化。当一个正车前进模式下的舰艇遇到突发事件需要紧急制动时,通常使螺旋桨在很短的时间内反向转动(ω<0)产生一个与舰艇运动方向相反的推力,此时舰艇由于惯性仍然保持前进而螺旋桨反转以使舰艇减速,这种应急操纵工况就被称为紧急倒车工况。
紧急倒车工况下螺旋桨反转引起局部的逆向流动与正向自由来流相互作用,使得螺旋桨周围流场十分复杂,为典型的三维非定常流场,其最显著的特征为桨盘面周围存在非对称的大尺度涡环结构。在试验测量方面,Hampton(1995)[2]在循环水槽中对螺旋桨P4381进行了紧急倒车试验,发现了这种处于周期性变化状态的涡环结构。后续有诸多学者利用LDV、PDV 和PIV 等流场测量仪器对紧急倒车流场与水动力性能展开了系列试验研究。Jiang 等(1997)[3]展示了涡环结构先顺流远离叶梢、破裂然后逆流返回桨盘面的运动规律;Jessup 等(2006)[4]观察到紧急倒车时桨叶区域的流动分离状态,并分析发现自由来流与螺旋桨反转诱导的逆向流动之间的相互作用产生了涡环结构;Bridges 等(2008)[5]发现涡环结构的非定常、不对称特性会产生偏离轴心的推力与扭矩,作用于螺旋桨并最终传递至艇体,影响潜艇的操纵性;Black 等(2009)[6]观测了紧急倒车工况下螺旋桨所受的应力与应变历程,发现周向速度对极端负荷事件的影响非常大。
在数值模拟方面,Chen 等(1999)[1]采用RANS 方法对P4381 的四象限敞水性能进行了数值模拟,正车前进工况的推力和扭矩计算结果与试验结果符合良好,但紧急倒车工况的计算结果与试验结果对比误差很大;Martin 等(2006)[7]采用大涡模拟方法对P4381 紧急倒车工况进行了研究,得到的推力、扭矩以及负荷的功率密度谱等计算结果均与试验吻合良好,证明了该方法的适用性。后续诸多学者采用LES 方法对紧急倒车工况开展了数值计算研究:Peter 等(2008)[8]发现流场瞬态的低/高频事件与涡环的不对称和振荡特性有关;Verma 等(2012)[9]发现潜艇所受侧向力主要由桨叶吸力面的导边分离产生,而艇体的存在会加大流动分离使得侧向力变大;Jang 等(2013)[10]发现紧急倒车流场有总体特征和局部特征,总体特征为正反向流动相互作用导致了涡环的产生,局部特征为螺旋桨桨叶导边与随边位置互换导致了流动分离;陈进等(2018)[11]研究发现涡环结构的位置极大地影响了桨叶表面的压力分布,并且当进速系数较小时,涡环形状偏小且更加靠近桨盘面。
从上述文献分析中可知,螺旋桨敞水状态紧急倒车工况下的流场十分复杂,而在潜艇的实际运行过程中,由于潜艇尾附体特殊的结构及布置形式,使得螺旋桨前端来流为非均匀流场,艇桨耦合状态紧急倒车工况下的湍流非定常特性和涡旋特征与敞水状态相比会更加明显,流动非定常特性更加难以计算。在国内外水动力学领域,以往对潜艇正常航行状态的研究较多,无论是模型试验,还是数值计算与仿真,研究成果都比较丰富,而对应急工况的研究较少,特别对紧急倒车工况的研究更少,不能满足实际工程应用需求,尚需开展更多深入研究。
本文采用大涡模拟方法分别对AU5-65 桨敞水状态以及SUBOFF 艇桨耦合状态正车前进与紧急倒车工况下的流场与水动力进行计算研究,对比分析紧急倒车工况下螺旋桨周围的非定常流动特征与大尺度涡旋结构,探讨潜艇紧急倒车工况的流动特征,阐释非定常流动机理,深化对紧急倒车精细流场的了解。作者利用商用软件FLUENT 在国家超算无锡中心上四节点(96 核)并行计算240 天完成全部研究内容。
1 计算方法与计算模型
1.1 大涡模拟控制方程
大涡模拟理论建立在两个基本假设之上:第一个假设是湍流的平均特性,主要由大尺度湍流运动来控制,几乎不受小尺度湍流运动的影响;第二个假设是小尺度湍流,特别在高雷诺数下,表现出各向同性的特点。因此,将非定常的N-S方程在波数空间或者物理空间上进行滤波,可得到大涡模拟控制方程,滤波后大于滤波尺度的涡通过直接求解N-S 方程得到,小于滤波尺度的涡通过亚格子涡模型(或称亚格子应力模型、亚格子模型)进行模拟。
滤波后的连续性方程和N-S方程可表示为
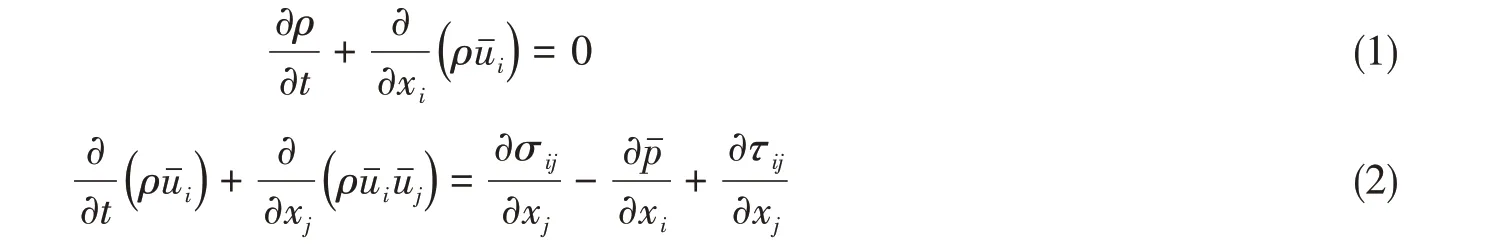

1.2 数值离散方法
动量方程差分格式为二阶迎风格式,压力差分格式为标准格式,时间差分格式为二阶隐式格式,压力速度耦合采用SIMPLE方法。时间步长Δt=5×10-5s,壁面y+≈1。
1.3 敞水性能系数
进速系数J、推力系数KT、扭矩系数KQ定义为以下形式:

式中,V表示来流速度,n为螺旋桨转速,D为螺旋桨直径,ρ为流体密度,T为螺旋桨推力,Q为螺旋桨转矩。
1.4 螺旋桨与潜艇模型
如图1 所示,计算模型选用AU5-65 螺旋桨与全附体SUBOFF 模型,AU5-65 是一个带有纵倾与侧斜的五叶螺旋桨,具体参数列于表1中。本文所用的SUBOFF潜艇模型的型值取自文献[13]。艇体总长为4.356 m,其中前体长为1.016 m,平行中体长为2.229 m,后体长为1.111 m,最大直径为0.508 m。指挥台长为0.368 m,上部为一个外凸的顶盖。四个尾翼对称布置于艇尾部,剖面均为NACA 0020 翼型。

图1 AU5-65桨与SUBOFF潜艇模型Fig.1 AU5-65 propeller and submarine model SUBOFF

表1 AU5-65螺旋桨基本要素Tab.1 Parameters of AU5-65 propeller
1.5 计算域与边界条件设置
计算域与边界条件相关设置参考了文献[14]。如图2 所示,敞水状态下螺旋桨前端为六倍桨径(D)的半球体,后端为十二倍桨径(D)的圆柱体。艇桨耦合状态下艇体前端为一倍艇长(L)的半球体,后端为两倍艇长(L)的圆柱体。入口与远场边界指定为自由来流边界条件,出口定义为压力出口边界条件,艇体和螺旋桨表面均为无滑移壁面边界条件。

图2 计算域与边界条件Fig.2 Computation domain and boundary condition
计算域由静止域与旋转域两部分构成,旋转域为包含螺旋桨在内的小圆柱体区域,如图2中红色区域所示,除此之外全为静止域,两部分之间由交界面(interface)连接,用滑移网格方法模拟螺旋桨旋转。
1.6 网格划分
为了精确捕捉流场涡旋结构并进行规范的网格收敛性研究,本文计算所用网格均为全域结构化网格,为保证桨叶和潜艇尾翼等复杂扭曲的区域也能生成高质量的结构化网格,本文参照文献[15-17],从建模到绘制网格均采用了多块分区的方法。
1.6.1 敞水状态下网格划分
在敞水状态下,参照ITTC 推荐规程绘制了全域结构化网格四套,网格数量分别为47 万、143 万、430万和1226万,四套网格的三向加细比均为 2。对四套网格进行计算分析后结合以往的计算经验,又在430 万和1226 万之间加设了1063 万网格,以同时满足计算精度与研究进度的要求。五套网格静止域与旋转域网格数量如表2 所示,五套螺旋桨表面网格如图3所示。
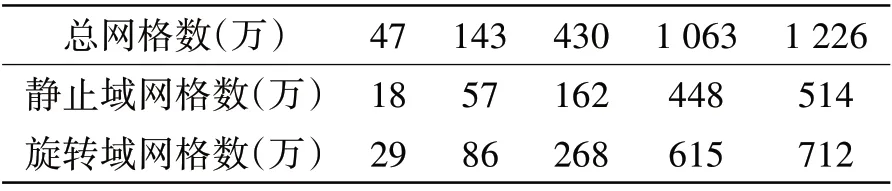
表2 五套网格Tab.2 Five sets of grids

图3 螺旋桨表面网格分布Fig.3 Mesh distribution on propeller surface
1.6.2 艇桨耦合状态下的网格划分
在艇桨耦合状态下,根据敞水网格收敛性分析选出最佳网格,保持其旋转域网格形式与数量不变,然后针对全附体SUBOFF 模型绘制了一套1489 万的静止域网格,艇体表面网格分布如图4 所示。艇桨耦合状态网格形式与数量设置依照以往研究[14-17]设定。

图4 潜艇表面网格分布Fig.4 Mesh distribution on submarine surface
2 计算方法验证
由于国内外水动力学领域都对螺旋桨正车前进状态的水动力与流场进行了很多试验研究,对于螺旋桨正车前进状态即第一象限的敞水性能曲线与流场特征已经有了很深入的认识,数据积累非常丰富,所以首先选用正车前进工况来验证计算方法。
2.1 网格收敛性研究
2.1.1 正车前进敞水性能计算分析
首先对AU5-65螺旋桨正车前进工况的流场与水动力进行计算并研究网格收敛性,计算在五套网格的四个进速(J=0.1、0.3、0.5 和0.7)下进行,计算得到的不同网格、不同进速下的推力与扭矩系数列于表3。将计算结果与试验结果进行对比后,计算误差列于表4。在数值模拟正车前进桨的敞水性能时,为与试验方法保持一致,采用了定转速变流速的方法,本文中转速都取为n=25 r/s。
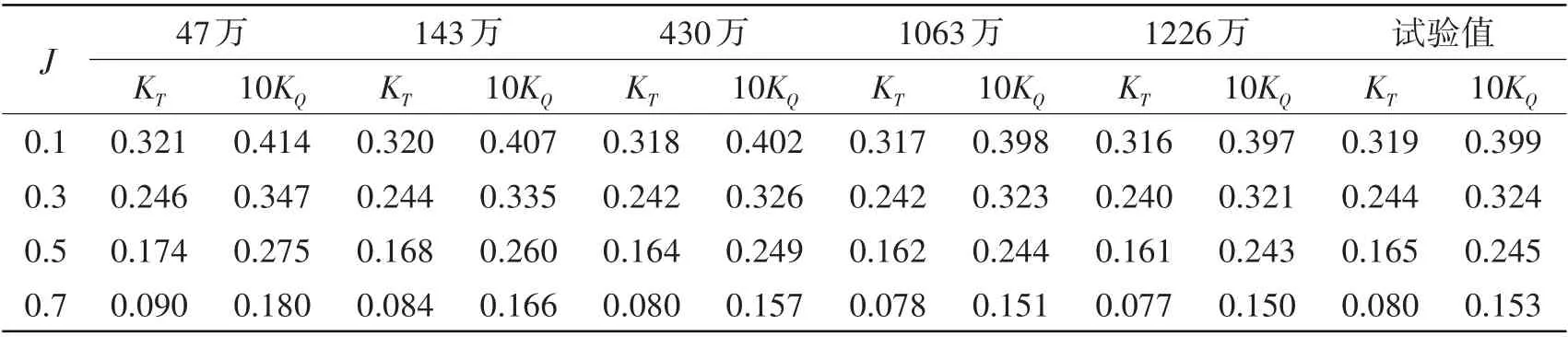
表3 不同网格计算结果与试验结果对比Tab.3 Comparison between computed results and measurements in different grids
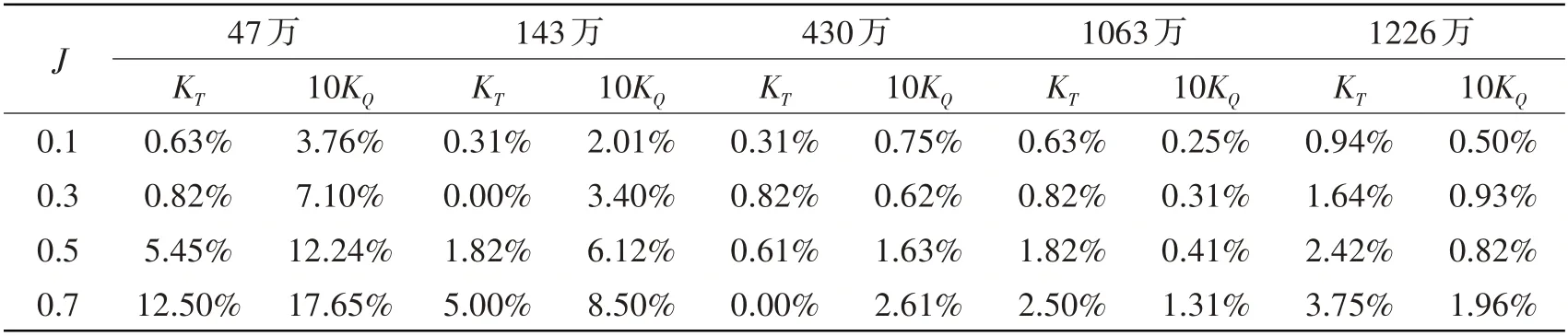
表4 不同网格计算误差Tab.4 Computational error of different grids
从表3 中可以看出,五套网格的计算结果呈现单调收敛的趋势,由430 万、1063 万和1226 万网格计算得到的水动力系数之间的差别非常小,相互之间的差异基本都在1.5%之内,从网格收敛性角度考虑,可知430万及以上数量的网格已经达到收敛性要求;从表4中可以看出,除47万与143万的计算结果与试验值相差较大之外,其余三套网格的计算误差均在4%以内,可知430 万网格已满足水动力的计算要求,更大数量的网格并不能进一步提升水动力计算结果的准确度,而是为后续精细计算非定常流动三维涡旋结构做基础。
2.1.2 正车前进涡旋结构计算分析
计算得到的不同网格在不同进速下的涡旋结构如图5 所示。纵向比较可以看到在同一进速下,随着网格数的增加,螺旋桨的梢涡与毂涡更加精细与完整。横向比较可以看到同一套网格下,随着进速的增大,流速增大,梢涡更加齐整与光顺。

图5 敞水正车前进涡旋结构Fig.5 Vortical structure of propeller in open water forward condition
本文采用Q判据捕捉涡旋结构,定义如下:

式中,ui、uj为三向速度,xi、xj为三向坐标。
针对涡旋结构可进一步探讨网格收敛性,此时发现430 万网格涡旋结构计算结果与1063 万网格和1226 万网格的计算结果还有一定差距,而1063 万网格和1226 万网格计算得到的螺旋桨周围涡旋结构差异很小,从涡旋结构数值计算角度来看,1063万网格已经达到网格收敛性要求。
综合分析螺旋桨敞水性能与涡旋结构计算结果后可以发现,1063 万网格已经可以较准确地辨识涡旋流场与计算水动力。因此,结合计算精度、计算时间与计算效率,最终选定1063 万网格来进行后续的敞水紧急倒车工况计算研究。
同时,由于敞水状态1063 万网格的旋转域网格数量为615万,因此与之相对应的艇桨耦合状态计算的网格数量为2104万,如表5所示。

表5 艇桨耦合状态计算网格数Tab.5 Computational grid in hull-propeller interaction condition
2.2 亚格子涡模型影响性研究
采用1063万网格,利用四种亚格子涡模型(SL、DSL、WALE 和KET)对AU5-65桨在正车前进工况四个进速系数(J=0.1、0.3、0.5和0.7)下的敞水特性分别进行计算,不同亚格子涡模型计算得到的不同进速系数下的推力与扭矩系数列于表6,计算误差列于表7。由表7 可知,在四种亚格子涡模型中,SL亚格子模型与试验值吻合最好,计算误差不超过3%,因此,初步选定SL 亚格子涡模型来进行后续的计算工作。
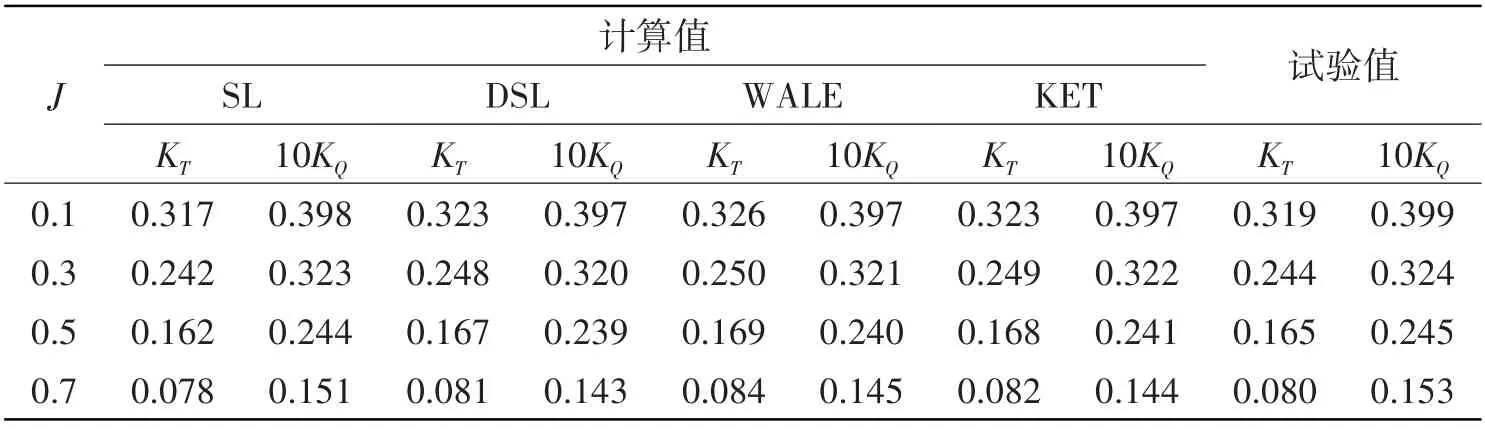
表6 不同亚格子涡模型计算结果与试验结果对比Tab.6 Comparison between computed results and measurements in different sub-grid stress models

表7 不同亚格子涡模型计算误差Tab.7 Computational error of different sub-grid stress models
2.3 SL模型在紧急倒车工况水动力计算应用中的验证
上节根据第一象限水动力的数值计算结果,得出SL 亚格子涡模型对水动力计算最优的结论,现将此模型应用于紧急倒车工况,进一步验证此模型对紧急倒车工况水动力的计算精度。
采用1063 万网格与SL 亚格子涡模型,对AU5-65 桨在五个进速系数(J=-0.1,-0.3,-0.5,-0.7,-0.9)下的紧急倒车工况敞水性能进行了计算,计算结果与计算误差列于表8,对应的敞水特性曲线如图6所示。
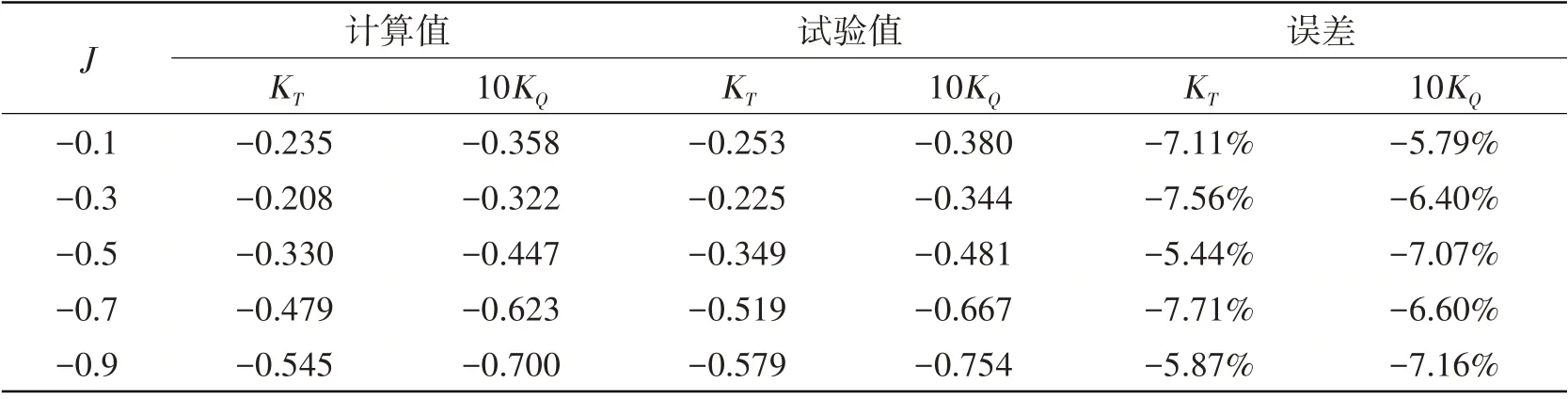
表8 紧急倒车计算结果与试验结果对比Tab.8 Comparison between computed results and measurements in crashback condition

图6 敞水紧急倒车特性曲线计算结果与试验结果对比Fig.6 Comparison of open water characteristic curves between computed results and measurements in crashback condition
紧急倒车流场为典型的三维非定常复杂流场,对其诱导水动力的计算比较困难,是当前的技术难点,国际上已有共识。从表8中可见,本文所采用的SL模型对紧急倒车工况下的推力与扭矩系数计算误差均在8%以内,与文献[10]中的误差量级基本一致,符合常规认识,计算结果比较令人满意,证明了计算方法与SL亚格子涡模型的可靠性。
综上,本文最终选定SL亚格子涡模型来进行后续的流场与水动力计算工作。
3 计算结果分析
3.1 敞水状态计算分析
3.1.1 涡旋结构计算分析
敞水状态正车前进工况下的涡旋结构计算分析见2.1.2节。图7为敞水状态紧急倒车J=-0.7时螺旋桨周围流场从5 周期到20 周期的演变过程,图中黑色圆环为螺旋桨所处位置。从图中可以看出紧急倒车工况下螺旋桨尾流非常复杂,在桨盘面之外有明显的非对称大尺度涡环结构,涡环以内有精细的中小尺度涡旋结构,不同形式与不同尺度的涡旋结构相互作用、缠绕并演化发展,向下游泄落。这种复杂的流动必然会对水动力与噪声产生显著影响。
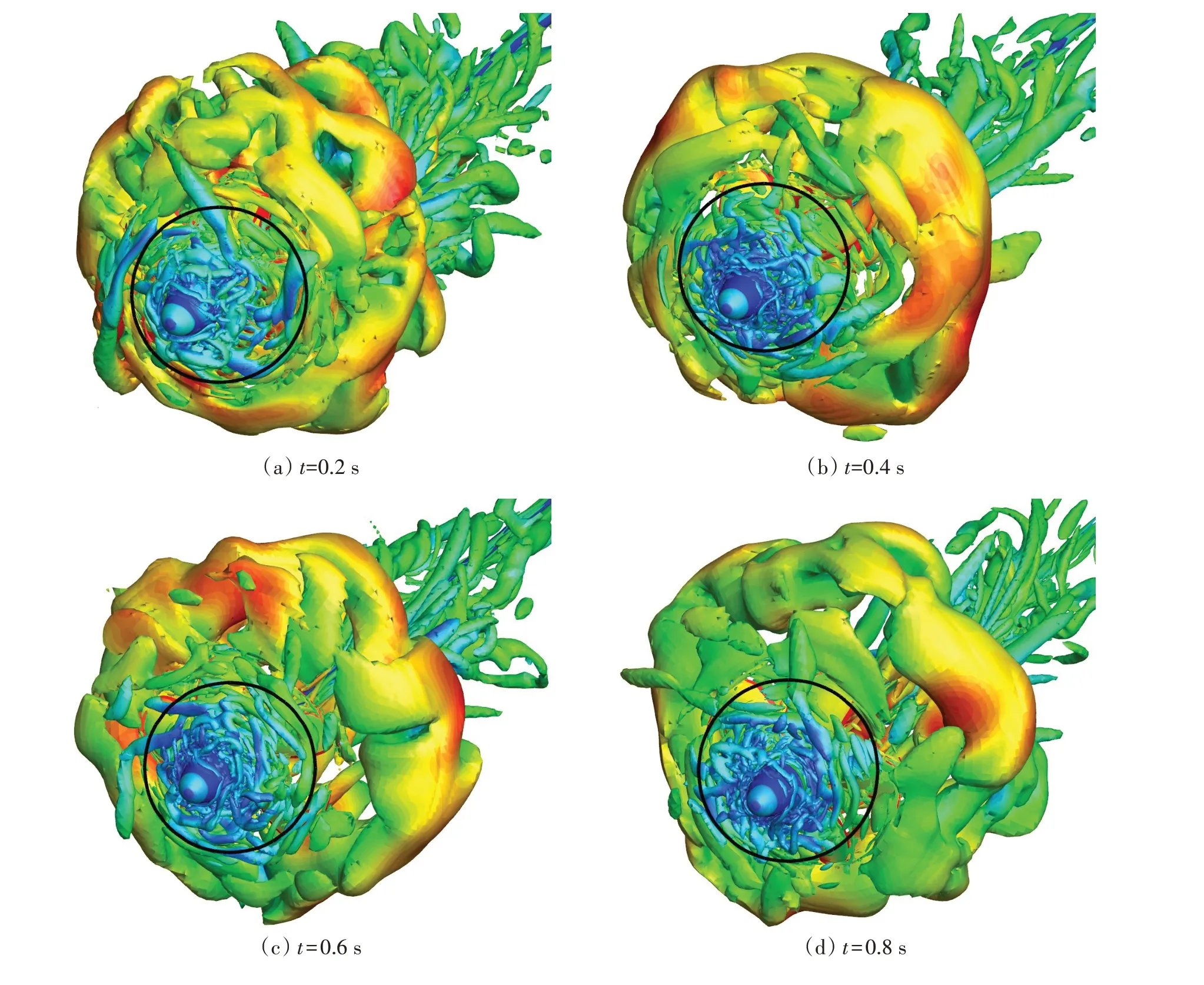
图7 敞水紧急倒车涡旋结构Fig.7 Vortical structure of propeller in open water crashback conditions
紧急倒车工况的大尺度涡环结构没有三维流动图像的测量结果,我们将本文的计算结果与文献[10]中的计算结果进行了对比,文献[10]中所用桨与本文的不同,但涡环的尺度与影响范围具有相似性,从侧面证明了本文计算结果是可靠的。
3.1.2 流场剖面计算分析
图8 为正车前进与紧急倒车工况横剖面与中纵剖面瞬态流场的对比图,分析可知正车前进工况下,流线光顺,流场较为平稳,而紧急倒车工况下螺旋桨周围流场非定常特征十分显著,桨后方有明显的涡旋结构,流场的复杂程度远大于正车前进流场。

图8 敞水正车前进与紧急倒车剖面流场对比Fig.8 Comparison of profile flow fields between open water forward and crashback conditions
从中纵剖面对比图中可以看出紧急倒车工况下涡环结构的成因是:螺旋桨反转诱导的强烈逆向流动与周围的自由来流相互作用产生了涡环结构。
图8(d)中涡环结构上部涡心纵向位于桨盘面之后0.48D处,垂向位于距桨轴中心0.72D处;下部涡心纵向位于桨盘面之后0.5D处,垂向位于距桨轴中心0.83D处,表明涡环结构非常复杂,不具有对称性。
3.1.3 水动力功率谱密度计算分析
将计算得到的推力与扭矩系数的时域信号进行傅里叶变换,得到正车前进与紧急倒车两个工况的推力与扭矩系数功率谱密度,如图9 所示,能量主要集中在低频段,紧急倒车工况下由于大尺度涡环结构的存在,湍流非定常特性十分明显,推力与扭矩功率谱密度比正车前进工况下高2~3 个量级,这必然将会对桨叶负荷和噪声等造成较大的影响。

图9 敞水正车前进与紧急倒车功率谱密度对比Fig.9 Comparison of PSD between open water forward and crashback conditions
3.2 艇桨耦合状态计算分析
本节主要探讨艇桨耦合状态下的潜艇尾部流场,特别是潜艇的存在对紧急倒车大尺度涡环结构的影响。为了与敞水状态进行对比,入口边界的来流速度与螺旋桨转速都与敞水状态保持一致。
3.2.1 涡旋结构计算分析
采用2104万网格和SL亚格子涡模型,对带有AU5-65桨的SUBOFF潜艇在敞水进速系数J=0.7与J=-0.7 时的水动力与流场进行数值模拟。计算得到的艇桨耦合状态在敞水J=0.7 时的尾流场涡旋结构如图10 所示,两图分别展示了尾翼马蹄涡初生以及成型状态下的潜艇尾流场,数值计算结果清晰地再现了艇桨耦合状态下的尾翼马蹄涡、螺旋桨桨叶梢涡以及毂涡等流动结构,再次证明了网格与计算方法的可靠性。
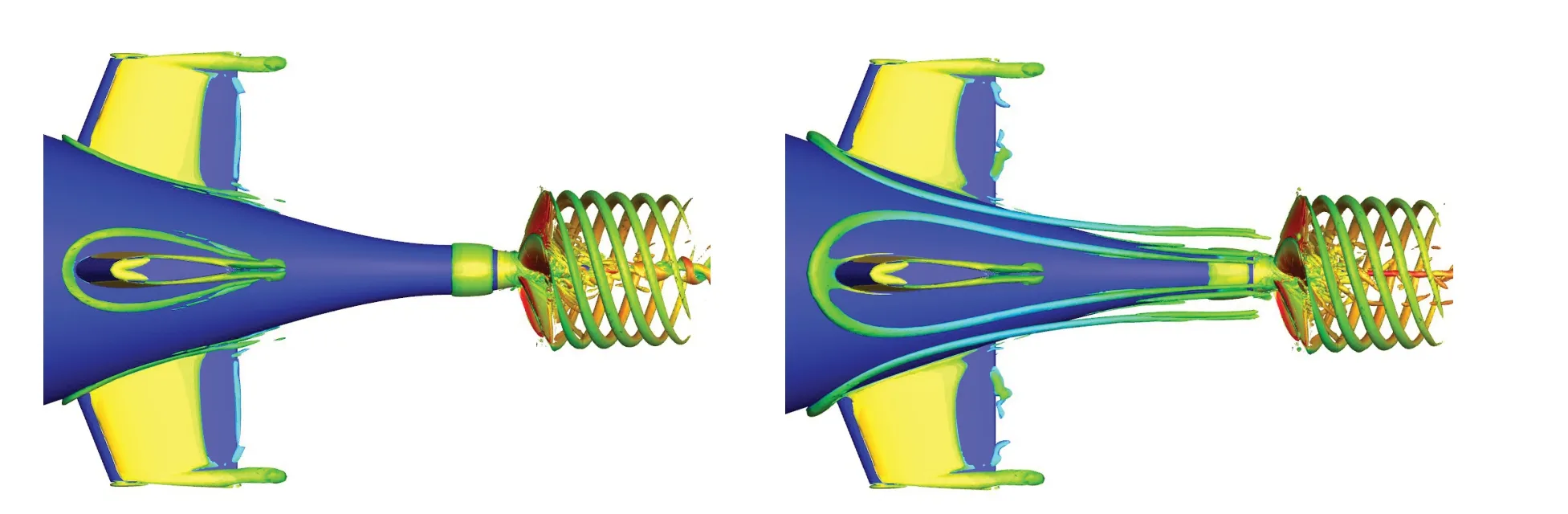
图10 艇桨耦合正车前进工况涡旋结构Fig.10 Vortical structure of submarine tail flow field in hull-propeller interaction forward condition
计算得到的艇桨耦合状态在敞水J=-0.7 时的涡旋结构如图11 所示,与敞水紧急倒车工况类似,螺旋桨周围有大尺度涡环结构的存在,同时由于潜艇尾部不均匀入流场的影响,涡环结构的形式与尾部的精细流场要比敞水状态下更加复杂。
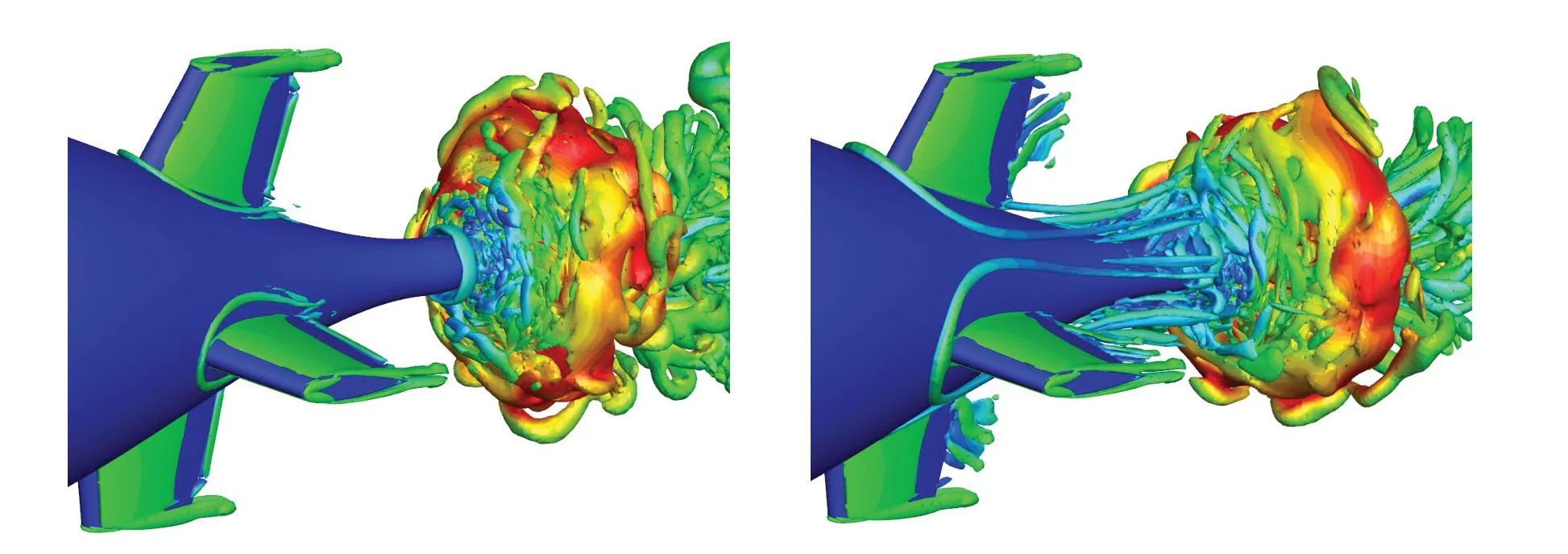
图11 艇桨耦合紧急倒车工况涡旋结构Fig.11 Vortical structure of submarine tail flow field in hull-propeller interaction crashback condition
3.2.2 流场剖面计算分析
图12 为两种不同工况下的流场剖面对比,虽然潜艇的存在使得螺旋桨来流不再均匀,但正车前进工况下螺旋桨周围流场仍比较稳定,流速分布较为均匀。紧急倒车工况下由于涡环结构的存在使得流场十分复杂,涡旋特征非常明显。图12(d)中涡环结构上部涡心纵向位于桨盘面之后0.35D处,垂向位于距桨轴中心0.64D处,下部涡心纵向位于桨盘面之后0.32D处,垂向位于距桨轴中心0.56D处,均小于对应敞水状态下的距离,表明艇体的存在会使涡环结构更加靠近桨轴中心,艇体壁面有“吸引”大尺度涡环的作用。

图12 艇桨耦合正车前进与紧急倒车剖面流场对比Fig.12 Comparison of profile flow fields between hull-propeller interaction forward and crashback conditions
为进一步探讨涡环的非定常特性,分别取敞水J=-0.7与对应艇桨耦合状态计算稳定后的第15到第20这六个周期的涡环结构中纵剖面,根据不同剖面内上下涡心所处位置相对于桨轴中心的纵向与垂向距离绘制成涡心运动轨迹图,如图13所示。可以看出,涡环结构的运动不具备明显的规律性,上下涡心的运动规律并不同步,敞水状态的上下涡心到桨轴中心的纵向与垂向距离均大于对应艇桨耦合状态。

图13 涡环结构中纵剖面涡心的运动轨迹Fig.13 Motion trajectory of vortex centers in longitudinal section of vortex ring structure
3.2.3 桨叶切面压力分布计算分析
图14为艇桨耦合状态正车前进与紧急倒车工况下0.7R桨叶切面周围带流线的压力分布云图,可以看出正车前进工况下的流线光顺,低压区在桨叶左侧吸力面中间区域,压力分布为典型的第一象限形式。紧急倒车工况下螺旋桨反转,桨叶导边与随边、压力面与吸力面位置与功能逆置,诱导局部的逆向流动与正向的自由来流在桨叶周围相互作用产生环状涡结构,低压区位于桨叶右侧(流动下游);图14(b)中桨叶切面轮廓右下方的导边(正车时随边)边缘存在大幅压差,并且由于反向的流动在导边(正车时随边)附近攻角较大,所以此时桨叶导边(正车时随边)周围也是最容易发生流动分离的地方。
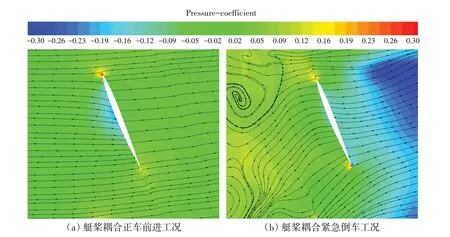
图14 桨叶0.7R切面压力分布Fig.14 Pressure distribution of blade section at r=0.7R
3.2.4 水动力功率谱密度计算分析
图15为艇桨耦合状态正车前进与紧急倒车工况下的推力与扭矩系数功率谱密度曲线图,与敞水状态下类似,能量主要还是集中在低频段,且紧急倒车工况下的推力与扭矩功率谱密度比正车前进工况下高2~3个量级。

图15 艇桨耦合正车前进与紧急倒车功率谱密度对比Fig.15 Comparison of PSD between hull-propeller interaction forward and crashback conditions
将不同工况下的敞水与艇桨耦合状态功率谱密度进行对比可知:由于潜艇尾部不均匀入流的影响,艇桨耦合正车前进工况下的功率谱密度比敞水正车前进工况下的高一个量级;而艇桨耦合紧急倒车工况下的功率谱密度在低频段和高频段比敞水紧急倒车工况下的高不到一个量级,在中频段(100~500 Hz)两者相差无几。表明艇桨耦合紧急倒车工况下大尺度涡环结构诱导的非定常效应要远大于非均匀入流的影响。
4 结 论
本文采用大涡模拟方法(LES)对螺旋桨紧急倒车这一非定常运行状态进行了计算研究。首先对AU5-65螺旋桨正车前进与紧急倒车的流场与水动力进行了计算分析,主要研究了网格收敛性与亚格子涡模型影响性,确定了计算要素,并通过相应的敞水试验数据对计算方法进行了验证;随后采用上述计算方法对带有AU5-65 桨的SUBOFF 潜艇在正车前进与紧急倒车工况下的流场与水动力进行了计算研究,分析了紧急倒车工况下的三维非定常复杂流场和大尺度涡环结构等流动特征;最后将不同工况下的流动结构、瞬态流场信息和水动力功率谱密度等进行了对比,分析了紧急倒车非定常流动机理和艇桨耦合效应。计算得到的主要结论如下:
(1)本文采用了47 万、143 万、430 万、1063 万和1226 万五套全域结构化网格进行收敛性研究,计算结果清晰地反映了水动力与流场随网格数的变化规律,综合考量后选定1063万网格来进行敞水紧急倒车工况的计算,对应的艇桨耦合状态计算网格数为2104万。
(2)在亚格子涡模型影响性研究中,SL亚格子涡模型的计算结果与试验结果对比误差最小,该模型在敞水正车前进工况下的计算误差不超过3%,紧急倒车工况下的计算误差不超过8%,计算精度与国际上的研究一致。
(3)计算所展现敞水状态与艇桨耦合状态正车前进工况下的流场都比较稳定,潜艇尾翼马蹄涡、螺旋桨叶梢涡与毂涡等流动结构与实际流动情况符合良好。
(4)在敞水状态与艇桨耦合状态的紧急倒车工况中螺旋桨周围都出现了非对称的大尺度涡环结构,湍流涡旋特征非常明显,并且由于潜艇尾部不均匀入流的影响,艇桨耦合状态下的涡环结构以及尾部精细流场比敞水状态下更为复杂。
(5)计算得到的大尺度涡环结构的运动不具备明显的规律性,涡环结构的中纵剖面上下涡心的运动规律并不同步;艇桨耦合紧急倒车工况下涡环结构的中纵剖面上下涡心到桨轴中心的垂向与纵向距离均小于对应敞水状态下的数值,表明艇体的存在会使涡环结构更加靠近桨轴中心。
(6)紧急倒车工况下螺旋桨反转,桨叶导边与随边、压力面与吸力面的位置和功能逆置,在桨叶下游形成大范围的低压区;此工况下推力与扭矩系数功率谱密度要比正车前进工况下的高2~3 个量级,同时艇桨耦合紧急倒车工况下大尺度涡环结构诱导的非定常效应要远大于非均匀入流的影响。
综上所述,本文所建立的基于大涡模拟的数值计算方法可用于潜艇紧急倒车工况的流场与水动力研究,为下一步潜艇紧急倒车工况流激噪声的相关研究奠定了基础。

