浮式风机基础非对称式系泊系统设计方法
康思伟,梁明霄,孙红军,徐胜文
(1.中海油融风能源有限公司,上海 200335;2.上海交通大学海洋工程国家重点实验室,上海 200240)
0 引 言
系泊系统具有技术成熟、结构简单且运行中能量消耗较少等特点,通常被选为离岸浮式风机的定位系统。国内外学者针对浮式风机的系泊系统设计进行了大量的研究。Benassai等[1]提出一种针对浮式风机的系泊系统优化设计方法,对不同水深条件下的风机系泊缆长度和直径进行了优化,并在极限工况和事故工况下校核了系泊系统的性能;Campanile等[2]对一浮式风机分别设计了由6缆和9缆组成的两套系泊系统,分别在英国北海南部和北部不同环境条件下进行了数值模拟,并基于模拟结果对其参数进行了修改;Benassai 等[3-4]研究了三套候选浮式风机系泊系统在不同水深下的最优长度和直径,并在极限工况和事故工况下对这三套系泊系统的性能进行了校核。同时,API、DNV 等[5-7]国际标准化组织推出了一系列详细的规范,对系泊系统的性能及安全提出了明确的要求。
工作在海上的浮式风机通常需要定期维护保养,这就要求其系泊系统在满足风机定位要求的前提下,为运维船预留足够的靠泊空间。在这样的条件下,对称式的系泊系统将难以满足要求。为此,需要对离岸工作浮式风机的系泊系统进行非对称设计,以满足运维船靠泊的要求。为了解决非对称系泊系统在不同环境力方向定位能力相差较大的问题,提出浮式风机基础非对称式系泊系统设计方法,结合非占优排序遗传算法(NSGA-II)优化系泊系统参数,以保证风机基础全环境力方向上系泊定位的安全性。
1 集中质量模型
系泊系统设计需要对锚链进行精确的建模,集中质量法是常用的锚链数值模型之一[8-10],它能有效地考虑锚链的非线性特性。在质量集中法中,锚链被划分为多个分段,每个锚链分段的质量和所受的外力被集中到分段两端的节点上,这样锚链分段就可以被视为一个无质量的弹簧。图1集中质量模型为锚链质量集中模型示意图,图中的圆圈表示锚链分段的节点,折线表示无质量的弹簧,y1、y2、y3分别为节点1、2、3在固定坐标系下的坐标向量。
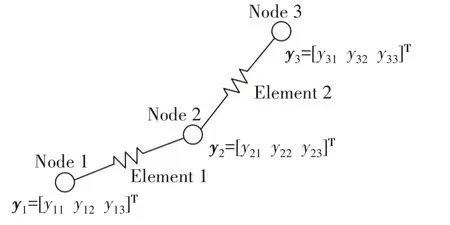
图1 集中质量模型Fig.1 Illustration of the lumped mass model
在利用集中质量法分析锚链时,每个节点的受力都应当满足控制方程:

式中:m为节点的质量矩阵;ÿ为节点加速度矢量;F为集中到节点上的外力,包括重力、浮力、锚链张力、拖曳力、惯性力、海底作用力、锚缆弯曲和扭转产生的作用力。
1.1 重力与浮力
任意一个浸没于水中的锚链分段,会同时受到重力和浮力的作用。以任意锚链分段j为例,其所受的重力与浮力的合力为

式中,Lj为锚链未拉伸时分段j的长度,ωj为锚链分段j的单位长度空气中质量,A为锚链的横截面积,ρ为海水密度,g为重力加速度。在集中质量法中,锚链分段的质量和所受外力被平均分配到分段两端的节点上。以节点2为例,其所受重力与浮力的合力G2为

1.2 锚链张力
对于任意一个锚链分段(例如锚链分段1),其弹性势能可表示为

式中,V1为锚链分段1的弹性势能,EA为锚链的轴向刚度,L1为锚链未拉伸时分段1的长度,|y2-y1|为节点1和节点2之间的距离。进一步地,锚链分段1作用在节点2上的张力可以由上式推导得到:
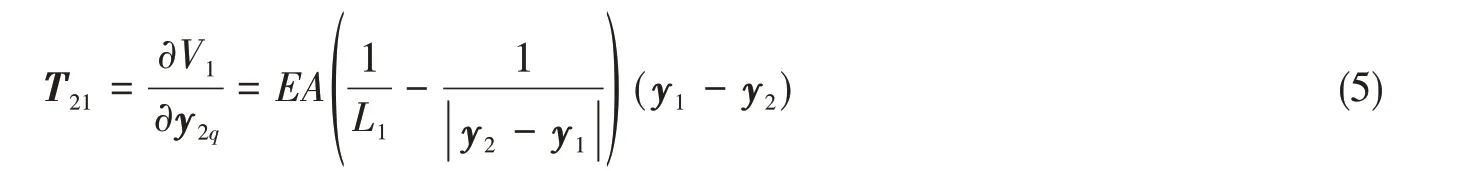
式中,q取1、2、3,分别表示固定坐标系下的X、Y、Z轴方向。
如此,可以求出作用在每个节点上的张力。以节点2为例,作用在节点2上总的张力T2为

1.3 拖曳力与惯性力

1.4 海底作用力
对于有躺底段的悬链式锚链,其拖底段会受到海底的作用力。在不详细研究锚链与海底相互作用力的前提下,一般认为锚链的锚点是不移动的且海底的弹性是线性的。
如图2所示,对于任意与海底接触的节点,海底对其的相互作用力可以等效为由三个平行于大地坐标系轴线方向的线性弹簧提供的力。以节点2为例,若其与海底相接触,海底对其的作用力可以表示为

图2 锚链与海底相互作用模型Fig.2 Illustration of seabed interaction model
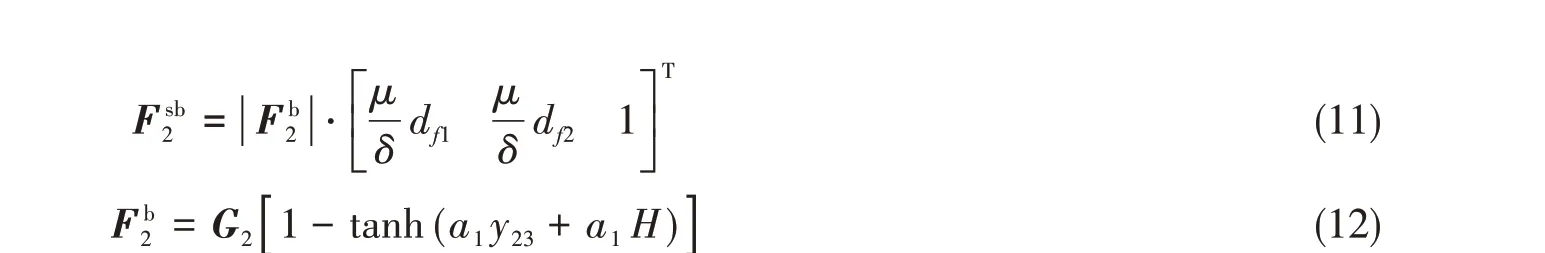
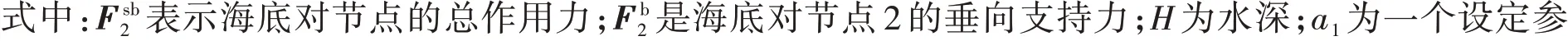

式中:q可取1或2,代表沿大地坐标系X或Y轴方向;y′2为节点2发生偏移后的位置;y2为节点2发生偏移前的位置。
1.5 锚链运动控制方程
对于时域下的锚链运动控制方程,可以使用Newmark-β法求解,其形式如下:

式中,α和β是精度调节参数。将上述方程代入控制方程可得
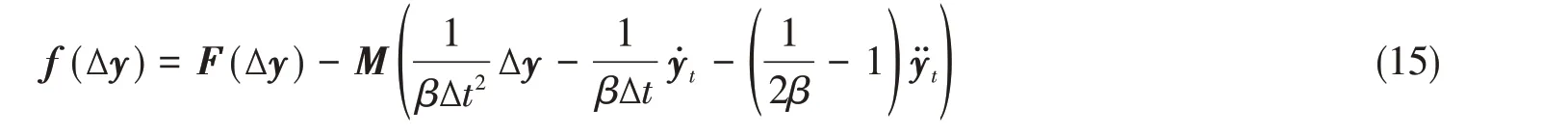
利用牛顿-拉夫逊迭代法求解方程即可得到Δy:

式中,下标m指代当前迭代步数,ε为修正参数,J为雅克比矩阵。
2 浮体-系泊系统全耦合数值模型
浮体与系泊系统的耦合作用是通过将浮体的运动方程和锚链的运动方程结合后实现的。浮体的运动控制方程如下:
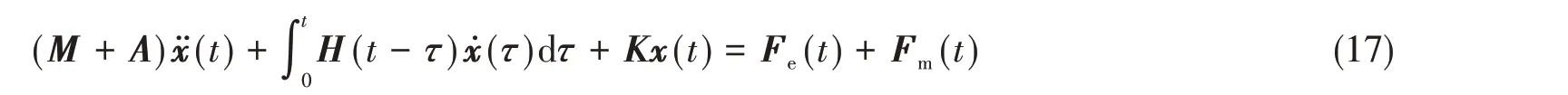
式中,M和A分别为浮体的质量和附加质量矩阵,H是浮体的时延函数矩阵,K是浮体的静水回复刚度矩阵,ẍ、ẋ和x分别是浮体的加速度、速度和位移向量,Fe和Fm分别为浮体所受的环境力和系泊力。
求解方程(17)中t时刻的系泊力,需要导缆孔在t时刻的位置信息作为边界条件。锚链导缆孔的位置信息需要依赖于浮体的位置信息,在系泊力未知的情况下,t时刻浮体的位置信息无法通过求解方程(17)得到。因此,本章引入弱耦合法求解方程(17)[11-12]。在弱耦合法中,系泊力的求解滞后于浮体位置信息的求解,即利用上一时间步的系泊力求解本时间步的浮体位置。
3 浮式风机基础非对称系泊系统设计方法
3.1 设计变量
系泊系统的设计和优化涉及到多个系泊系统的参数,主要包括锚链数量、锚链长度、公称直径、系泊半径、锚链方位角、材料等级和锚链结构等。材料等级和锚链结构需要在系泊系统设计之初事先确定。锚链数量、锚链长度、公称直径和系泊半径是四个独立的设计变量。锚链的干重、湿重及轴向刚度等参数则取决于锚链的公称直径、结构及材料等级,这些参数不是独立的,也不能作为优化设计变量。非对称的系泊系统包括锚链布置方式的非对称和不同锚链参数的非一致,浮式风机基础的非对称系泊系统设计主要针对的是前者。锚链的干重ω、轴向刚度EA及破断强度TMBL的计算公式如下:

式中:D为锚链的公称直径[13],单位为mm;干重ω的单位为kg/m;破断强度TMBL的单位为kN;轴向刚度EA的单位为kN。
3.2 目标函数
系泊系统的设计目标主要包括其定位性能和安全性能。对于不同的设计要求,系泊系统的定位能力可以由浮体的最大水平偏移或其他合适参数表征;系泊系统的安全性可以由安全系数、躺底段长度等具体参数表征。由于浮式风机工作环境的特殊性,其非对称式系泊系统设计目标还应当满足以下要求:
(1)非对称的浮式风机系泊系统在不同方向上的定位能力应尽量一致。
(2)非对称的浮式风机系泊系统安全性满足规范要求。
系泊系统的定位能力可以由系泊后浮式风机的最大水平偏移表示,而系泊系统的安全性可以由锚链的最大张力与其破断强度的比值来表征,其数学表达形式如下:

式中:ϕH、ϕS分别为系泊系统定位能力与安全性相关的设计目标函数;x为浮式风机的水平偏移;Tmax及TMBL分别为锚链的最大张力和最小破断强度。
除了上述两个目标函数外,还对浮式风机系泊系统的经济性提出要求,其具体的要求为:使系泊系统锚链长度和公称直径最小。因此,经济性目标函数可以表示为

式中:ϕL、ϕD分别为系泊系统锚链长度和公称直径相关的设计目标函数;L和D分别为锚链的长度和公称直径。
3.3 优化设计模型
经过前述分析可以看出,浮式风机的非对称系泊系统设计实质是一个多目标优化问题,其数学形式可以表达为

式中,Xi为设计变量,ϕi为目标函数,Ω为可行域,θi为约束条件。
求解上述多目标优化问题常用的方法有NSGA-II[14]、PESA-II[15-16]以及SPEA-II[17]等方法。由于NSGA-II方法相较于其他两种方法求解效率更高,在MATLAB[18]环境中编写了一套基于NSGA-II算法的程序并将其与系泊动力计算软件Orcaflex[19]耦合,用于求解系泊系统的优化设计问题,具体计算流程如图3所示。
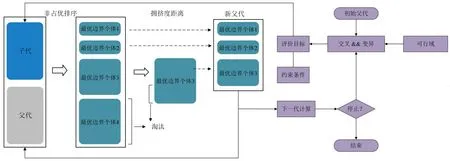
图3 优化设计模型计算流程Fig.3 Calculation flow of optimization design model
在计算开始时首先随机生成一个父代(Parent),通过交叉(Crossover)和变异(Mutation)算法产生新的子代(Child)。将父代和子代合并,计算合并后种群中个体(Individual)的非占优排名(Rank)和拥挤度距离(Crowding distance)。基于非占优排名和拥挤度距离选择较优的个体作为新的子代(Offspring)并在下一个循环汇中作为父代参与运算。在计算循环次数达到设定值后,结束运算并输出结果。
4 算 例
4.1 浮式风机参数
文中研究的浮式风机结构由3 个浮筒和塔架结构组成,如图4~5 所示。浮式风机吃水深度为20 m,中部立柱与三个浮筒间通过一系列较小直径的横梁连接,形成正三角形构型。风机的具体参数如表1所示。

图4 浮式风机基础结构示意图Fig.4 Schematic diagram of the floating wind turbine structure
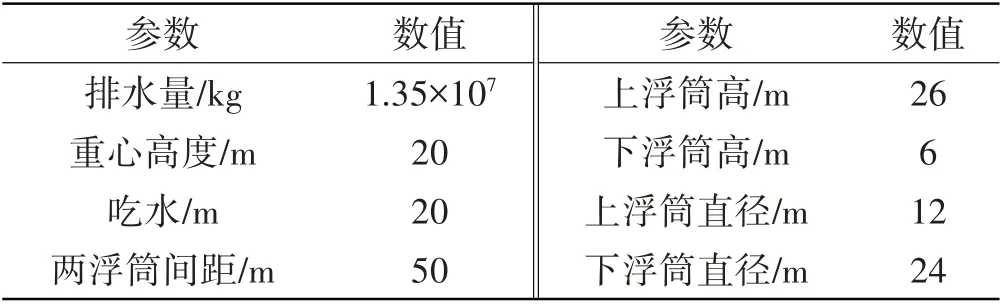
表1 浮式风机基础基本参数Tab.1 Main parameters of the floating wind turbine
浮式风机基础在浮筒外侧共布置有3 个导缆孔,导缆孔位置在浮体坐标系下的坐标如表2 所示。浮式风机在部署点的海洋环境条件为风速1.2 m/s、流速1 m/s,具体波浪参数见表3。为了研究系泊系统在各个方向上的定位能力,规定环境方向为0°~360°,每隔30°计算一次,同时规定风、海流、波浪的方向相同。
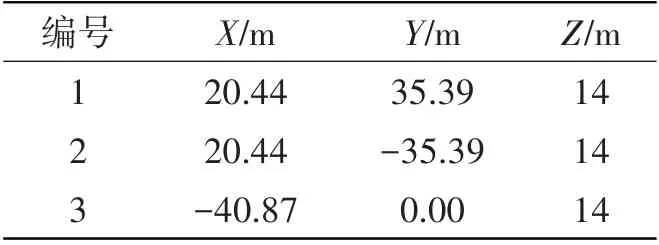
表2 导缆孔位置坐标Tab.2 Coordinates of the fairlead

表3 风机基础工作海况参数Tab.3 Wave parameters of the floating wind turbine in operational condition
该浮式风机基础工作于水深为200 m 的海域,在运营期间,需要运维船靠泊作业提供定期的维护保养。运维船在靠泊时,由X轴(图5)正方向逐渐靠近浮式风机,并在距离风机15~20 m 处定位。为了避免浮式风机的锚链与运维船发生碰撞,需要使锚链在靠泊处留出足够的空间。因此,在考虑运维船靠泊条件下的浮式风机系泊系统必须设计成非对称形式。
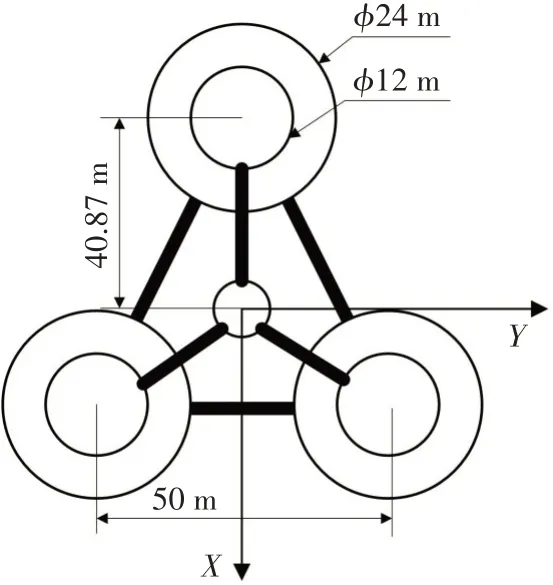
图5 坐标轴示意图Fig.5 Sketch of the coordinate system
4.2 浮式风机基础设计模型
为了保证浮式风机和运维船的安全工作,系泊系统的布置形式必须是非对称的,即锚链锚点的位置需要单独设计。如图6所示,规定每个导缆孔中伸出的两个锚链为一组,每组锚链的参数是独立的且每组中两个锚链间的夹角为10°。为保证系泊系统在各方向上具有一致的回复力,不妨使第1、2号锚链与第5、6号锚链的参数相同。如此,需要设计的锚链参数为第1、2、5、6号锚链的长度和直径L1、D1,第3、4号锚链的长度和直径L2、D2。锚点的位置可以由系泊半径和锚链的方位角确定。对于本例,由于系泊系统布置范围受限,锚链的系泊半径规定为800 m,第1、6 号锚链与X轴夹角α为需要设计的参数。

图6 系泊系统布置示意图Fig.6 Schematic diagram of the mooring system layout
系泊系统的优化设计目标包括系泊系统在各个方向的定位能力、系泊系统的安全性以及系泊系统的经济性,目标函数的具体形式如式(25)所示。
为了保证锚不受到过大的上拔力,需要系泊系统中锚链具有一定长度的躺底段,依据工程经验,规定锚链的躺底段长度不应小于20 m。该浮式风机在海上工作时需要定期维护保养,为保证运维船有足够的作业空间,规定角α的值应不小于60°。因此,在设计过程中还需要的约束条件有:
(1)锚链的安全系数不小于1.67,即ϕS≥1.67。
(2)锚链躺底段长度不小于20 m,即ϕT≥20。
(3)角α的值不小于60°,即ϕα≥60。
如前文所述,本例中的系泊系统设计多目标优化问题的数学形式可以表示为

式中,i表示不同的环境方向。
设置NSGA-II 的种群数量为50,迭代步数为60。设置Orcaflex[19]模拟时间为10 800 s,时间步长为0.2 s。各设计变量的可行域如表4所示。

表4 系泊系统设计参数可行域Tab.4 Feasible region of design parameters for mooring systems
4.3 非对称系泊系统优化设计方案
计算完成后,总共得到10个最优解。基于Liang 等[21]提出的筛选方法对候选结果进行分组,即最优解空间距离接近的解等效为1个解,如此,得到3组最优解,参数如表5所示。

表5 候选系泊系统参数Tab.5 Main parameters of designed candidate mooring systems
如表5所示,所得最优解的角α均接近其取值范围下限,为60°左右。在设计时要求系泊系统在各个方向上的定位能力一致,为了有效抵抗环境力,优化过程中NSGA-Ⅱ算法向减小角α的方向搜索最优解,并最终使最优解的角α值在其下限附近波动。由于浮式风机的系泊系统是不对称的,在系泊系统布设完成后浮式风机会出现初始偏移,并达到新的平衡位置。在环境力的作用下,浮式风机会在初始偏移后的新平衡位置附近振荡。三组最优解对应的初始偏移和最大水平偏移分别为0.81 m、3.40 m、1.40 m和5.2 m、8.2 m、5.7 m,三组结果中最大偏移约为水深的4.1%。总体看来,浮式风机在新平衡位置振荡幅值不超过5 m。进一步对比垂向力可以发现1 号和3 号备选系泊系统的垂向力较大,分别为10 374 kN和10 768 kN,约比2号备选系泊系统大1300 kN。三组备选系泊系统中,在安全系数相差不大的情况下,1 号系泊系统具有最小的水平位移和初始水平位移。虽然1 号系泊系统的垂向力稍大,但也仅比最小值高出917 kN。
图7~8中给出浪向角为180°时,浮式风机在2000 s至4000 s内的六自由度运动时历。观察图7可以发现,浮式风机在2 号系泊系统约束下纵荡运动的平均位置距离原点较近,同时在3 号系泊系统的约束下浮式风机的垂荡平均位置更远。由表5中所示结果可知,在2号系泊系统作用下浮式风机的初始偏移相对更远,这表明2号系泊系统初始时具有一个较大的、指向X轴正方向的初始回复力,因此2号系泊系统能更好地抵抗180°浪向下的环境力。由图8可以发现,2号系泊系统约束下浮式风机的纵摇平均值略大,而浮式风机的横摇和艏摇运动几乎一致。这表明在浪向为180°时,三组系泊系统的横摇、纵摇和艏摇回复力特性相差不大。
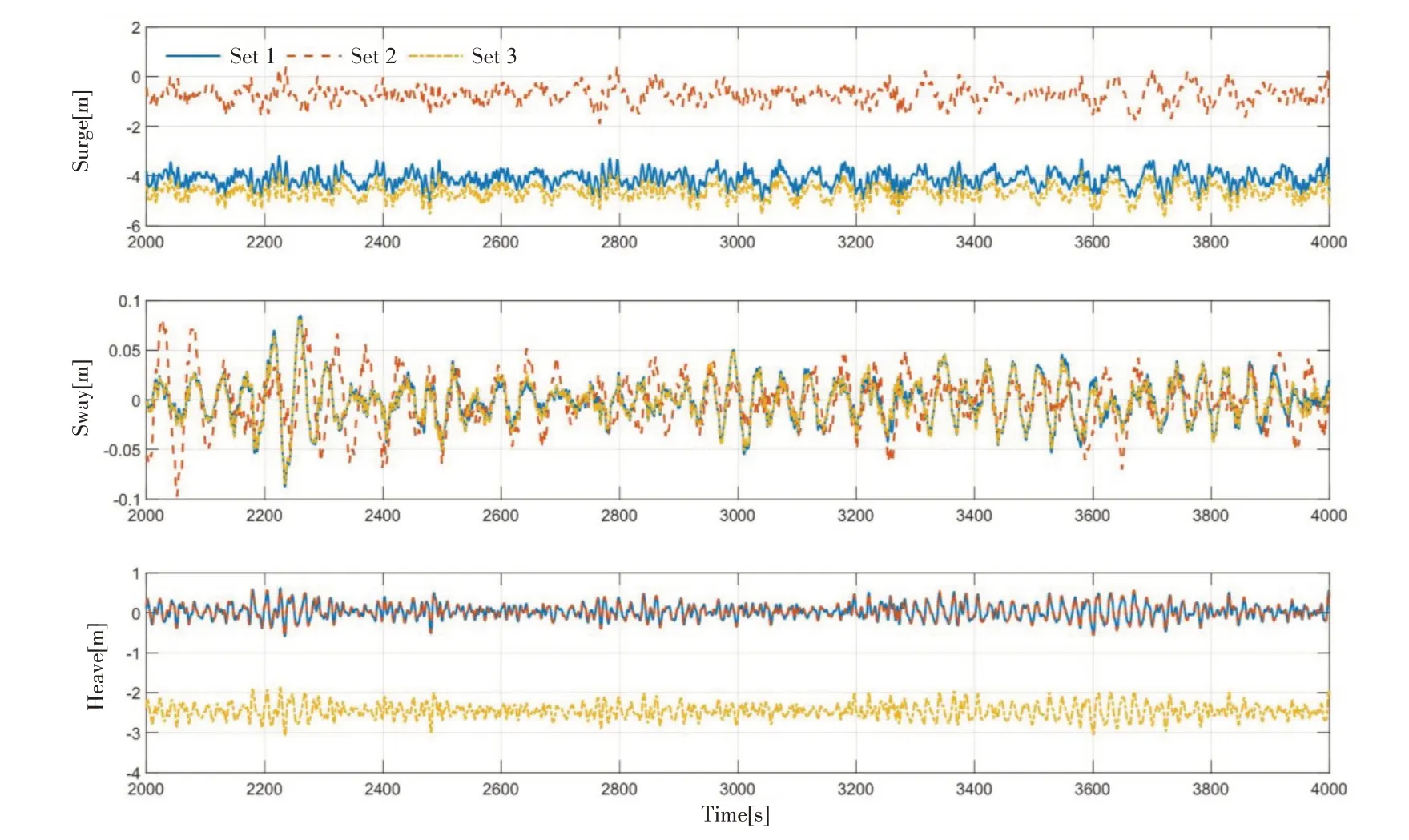
图7 180°浪向下风机基础纵荡、横荡和垂荡运动时历Fig.7 Time history of surge,sway and heave motion of the floating wind turbine under 180°wave direction
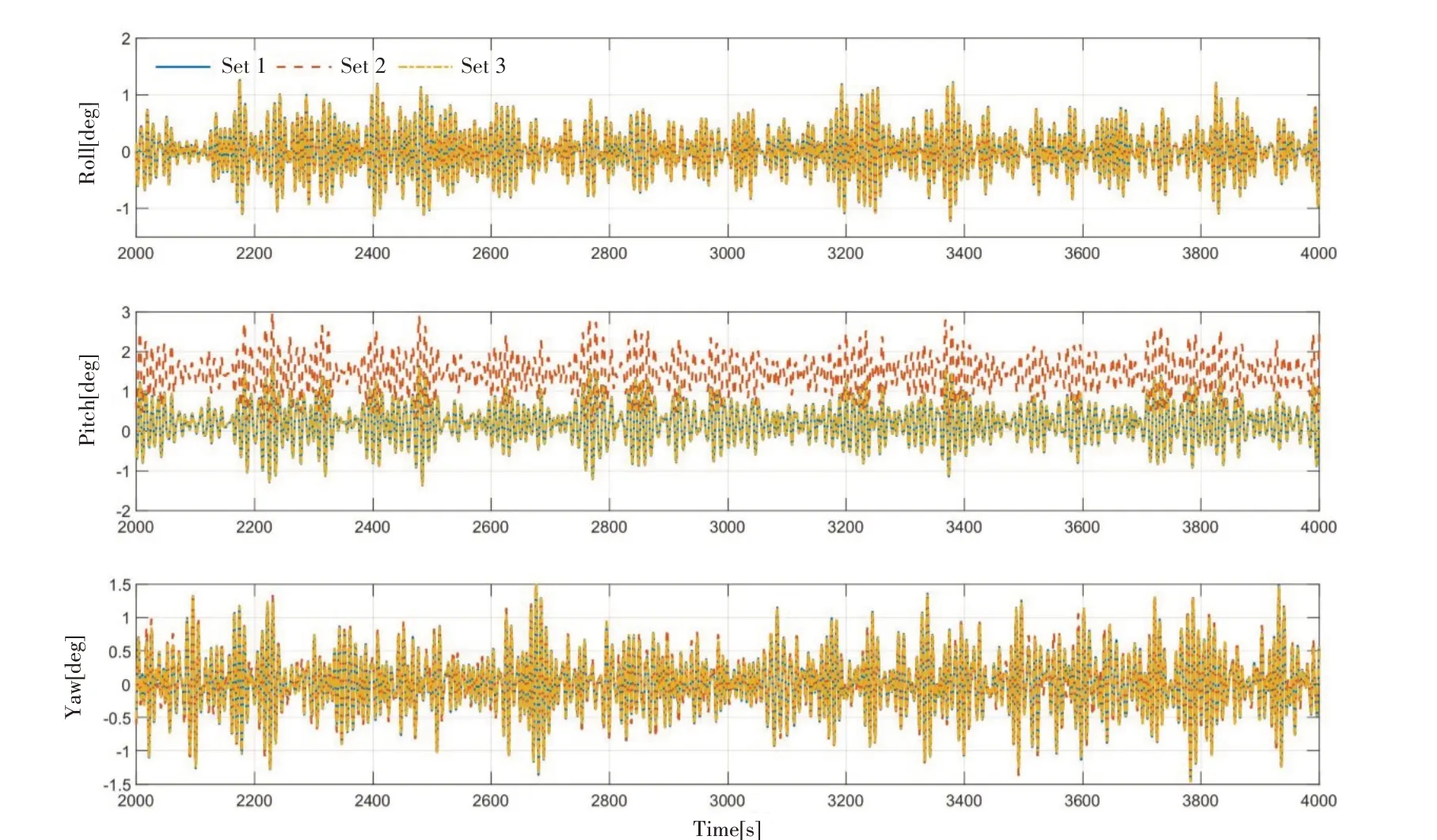
图8 180°浪向下风机基础横摇、纵摇和艏摇运动时历Fig.8 Time history of roll,pitch and yaw motion of the floating wind turbine under 180°wave direction
为进一步对比三个候选系泊系统的定位能力,图9~11中给出了其在不同方向环境力作用下浮式风机的最大水平位移。对比图中结果可以发现,1号、3号系泊系统约束作用下,风机基础在各个方向的最大和平均水平位移都能较为均匀地分布在初始平衡位置周围。3 号系泊系统约束作用下,风机基础在环境力作用下的水平位移主要集中在X轴正方向上,这是由于系泊系统的初始平衡位置向X轴正方向上偏移过多而造成的,而这一结果带来的一个不利影响是3 号系泊系统在X轴正方向上的定位能力较弱。表6中给出了三组系泊系统在不同环境力方向下的安全系数。从表中数据可以看出,三个候选系泊系统的安全系数均远大于要求值1.67,其中1 号和3 号候选系泊系统在各个方向上的安全系数约为4.6~5.5,而2 号候选系泊系统则稍大,约为4.5~6.3。
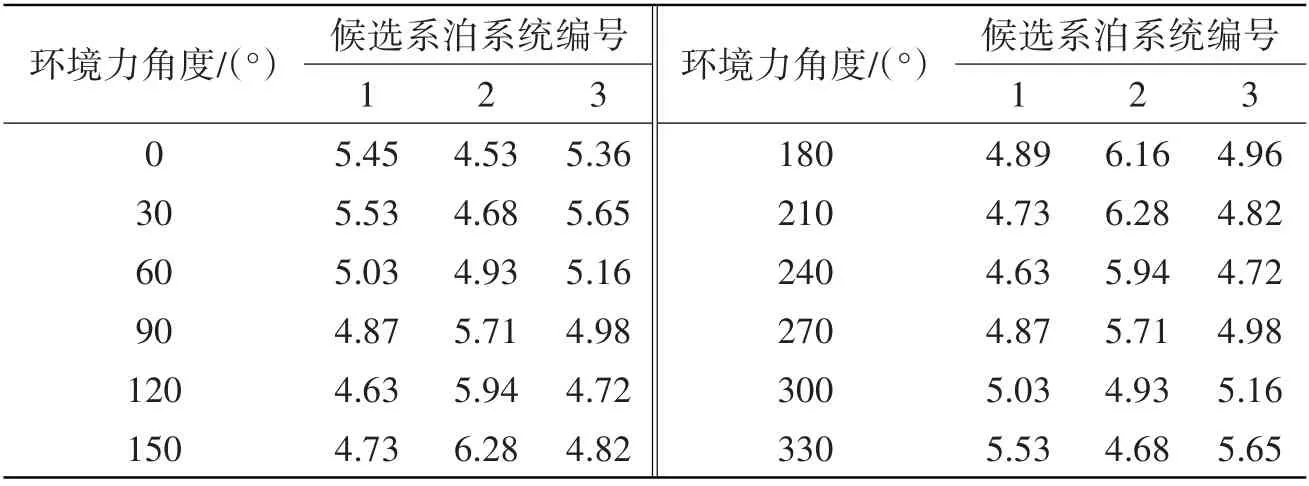
表6 候选系泊系统安全系数Tab.6 Safety factors of designed candidate mooring systems

图9 1号系泊系统下风机基础不同环境力方向水平位移统计值Fig.9 Statistical values of horizontal displacement of the floating wind turbine with No.1 candidate mooring system in different environmental force directions
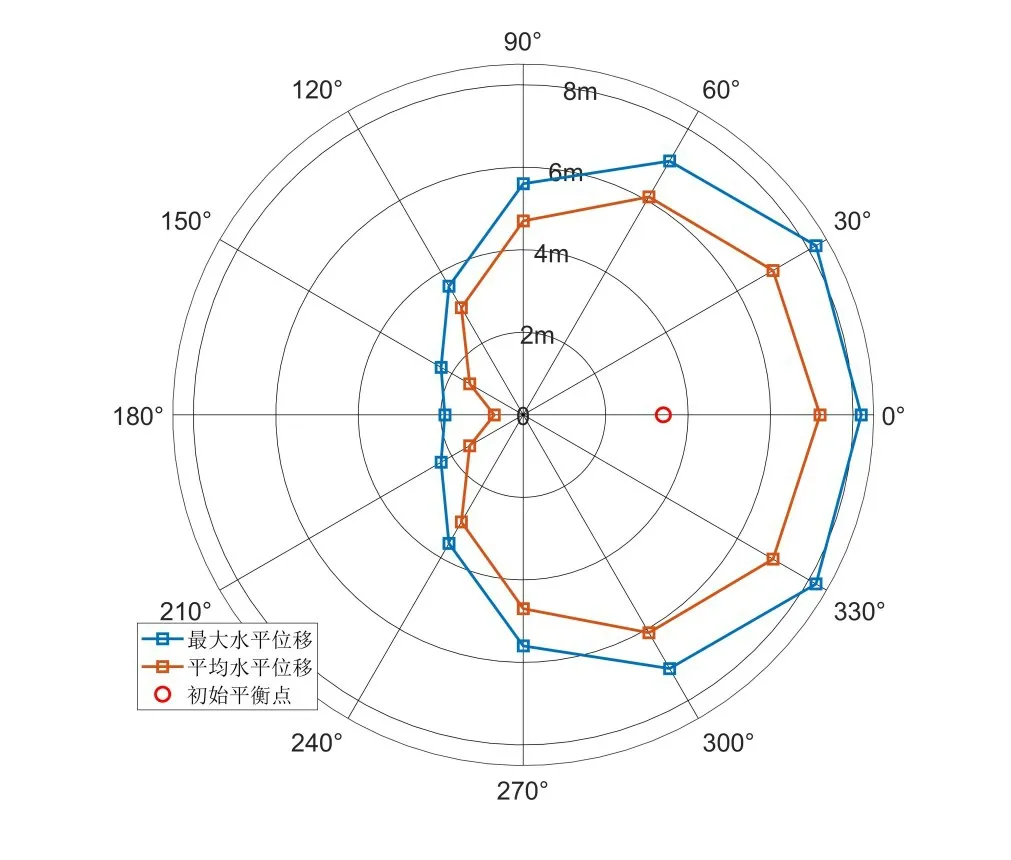
图10 2号系泊系统下风机基础不同环境力方向水平位移统计值Fig.10 Statistical values of horizontal displacement of the floating wind turbine with No. 2 candidate mooring system in different environmental force directions
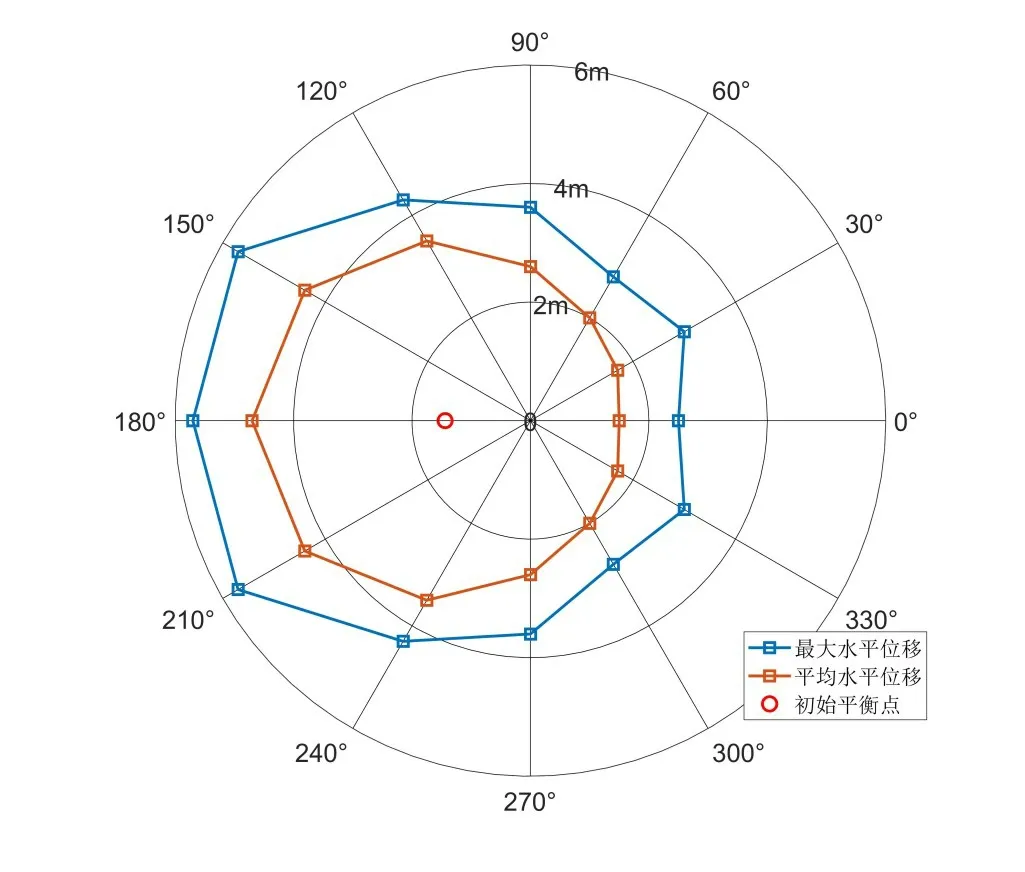
图11 3号系泊系统下风机基础不同环境力方向水平位移统计值Fig.11 Statistical values of horizontal displacement of the floating wind turbine with No. 3 candidate mooring system in different environmental force directions
综上所述,1号、3号系泊系统都能满足系泊系统在各个方向上定位能力基本一致的要求,且不同方向上系泊系统的安全系数均大于要求值。相较于3 号系泊系统,1 号系泊系统约束作用下,风机基础的初始水平偏移更小,因此选择1 号系泊系统作为最终设计的浮式风机系泊系统,具体参数如表7所示。

表7 选定风机基础非对称系泊系统详细参数Tab.7 Detailed parameters of the selected asymmetric mooring system for the floating wind turbine
5 结 语
浮式风机运行期间通常需要进行定期维护保养,这要求其系泊系统在满足浮式风机定位要求的前提下,为运维船靠泊作业预留足够的空间。由于常用的对称式系泊系统无法满足要求,本文提出了浮式风机基础非对称式系泊系统设计方法,结合非占优排序遗传算法(NSGA-II)优化系泊系统参数,以保证风机基础全环境力方向上系泊定位安全性。对某浮式风机基础开展了非对称式系泊系统设计,得到的系泊系统在各个方向上的定位能力基本一致,且其安全系数大于规定的目标值,证明了提出的浮式风机非对称式系泊系统设计方法的有效性。

