电磁直驱变速器热网络建模与热特性研究

王磊，陶文明，司书哲，边文斌，陈杰炜，陆佳瑜，张宇

（1.255400 山东省 淄博市 舜泰汽车有限公司；2.255049 山东省 淄博市 山东理工大学 交通与车辆工程学院）

0 引言

在当前新能源汽车技术条件背景下，汽车的续航里程和动力性均受制于电池模组的技术瓶颈[1]，寻找其他解决方案以提升新能源汽车的动力性和经济性成为必然。作为汽车传动系统重要组成部件的变速器，可以通过改变挡位选取适合的传动比，让电机始终工作在高效区的同时，使车辆具有最佳的动力性和经济性。但在换挡过程中，变速器内部由于摩擦等原因产生大量的热，热量无法及时散出时导致其内部产生温升现象，进而影响换挡性能。因此，研究变速器的发热机制、传热过程及温度分布，对于改善其换挡性能有着重要的意义。

国内外的学者针对变速器工作时的温度变化进行了一系列的研究。Chen[2]等采用热网络法研究了双速变速器在不同转速下的外壳和齿轮等零件的温度，但在模型简化时忽略了对流换热效应；李卓富[3]利用ADAMS 对变速器进行动力学仿真，在Pro/E 中建立模型并导入ANSYS 中进行齿轮温度分析；Wurm[4]等提出了一个可预测无级变速器温度变化的模型，采用了流体力学计算方法和多重坐标系建立了齿轮组的运动模型，并对齿轮温升进行了仿真；Changenet[5]等基于一种6 挡手动变速器提出了一种功率损失的预测模型，综合考虑了齿轮、轴承、同步器以及润滑油等部分的热量损失，并通过实验验证模型预测效果与实际比较吻合。

目前国内外对变速器稳态热特性分析的研究越来越多，但这些研究大多是针对变速器内部零件的研究，缺乏对整个系统的全面分析，同时很少涉及同步器与摩擦锥面的研究，导致仿真模型与实际有一定偏差。本文采用了热网络法对合作高校课题组提出的一种电磁直驱变速器工作时其内部的温度变化进行研究。通过对变速器内部各摩擦副产热机理进行分析，建立了热网络模型，并仿真计算得出了变速器内部温度变化。

1 电磁直驱变速器结构及热功率损失建模

1.1 电磁直驱变速器结构及工作原理

本文的研究对象是基于合作高校课题组自主研发的2 挡直驱式自动变速器，电机结构如图1 所示，主要包括输入轴总成、输出轴总成、换挡执行器及壳体4 部分，换挡执行器布置在两挡输入齿轮中间，输入、输出轴通过高速轴承固定在壳体上，壳体两侧有固定轴承的端盖。

图1 电磁直驱变速器示意图Fig.1 Diagram of electromagnetic direct drive transmission

当换挡执行器处于中间位置时，固定在动子线圈骨架上的同步器结合套与两挡齿轮齿圈处于分离状态，此时变速箱处于空挡。当驾驶员进行换挡时，变速器控制单元（TCU）收到所需挡位的换挡指令，使动子线圈两端电路导通，执行器接入该挡位方向的通电电流，在电磁力的作用下实现轴向方向的双向移动完成换挡。

1.2 热功率损失建模

电磁直驱变速器工作时，内部因摩擦造成的功率损失主要包括3 方面：同步器与摩擦锥面间摩擦生热、输入与输出轴齿轮啮合面间摩擦生热以及轴承滚子与内外滚道间摩擦生热。

1.2.1 同步器热功率损失建模

同步器作为变速器的主要零部件之一，其工作时的受力分析如图2 所示。由图2 的受力分析可知同步器摩擦副摩擦力矩的等效作用力Fl为：

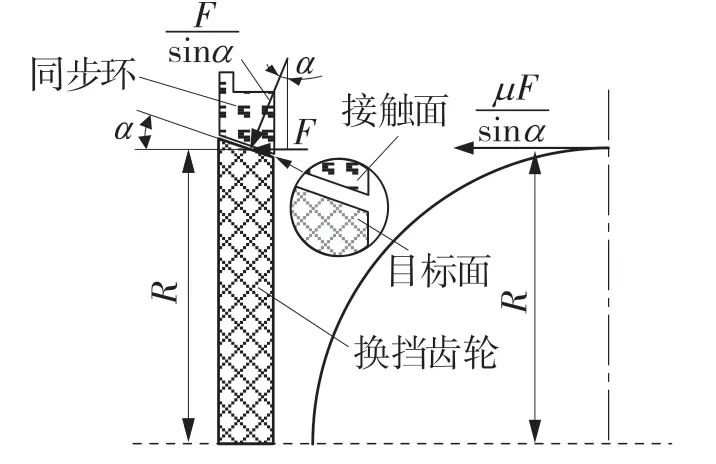
图2 同步环与摩擦锥面受力分析图Fig.2 Analysis of forces on synchronizer ring and friction cone

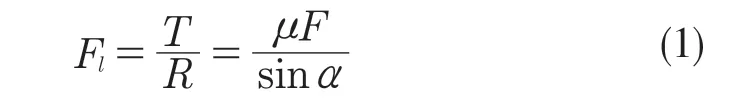
式中：T——摩擦副摩擦力矩；R——接触面的平均半径；μ——摩擦系数；F——作用在同步环上的轴向换挡力；α——摩擦锥面半锥角。

目前，针对摩擦功率损失的研究方法主要有3种[6]，本文采用解析计算法快速模拟出不同工况下摩擦对偶面间的摩擦功率损失，对各摩擦副的摩擦热功率损失进行计算。

同步器摩擦副接触面由于摩擦生热产生的总热功率损失为[7]：

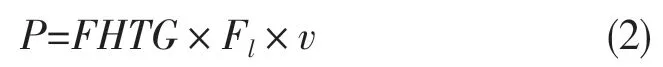
式中：FHTG——摩擦生热的能量换算因子；v——摩擦副部件相对滑动速度。

1.2.2 齿轮热功率损失建模

在两挡齿轮啮合过程中，输入、输出齿轮间的相对运动形式为滑动摩擦和滚动摩擦[8]。

滑动摩擦是齿轮在啮合处由于相接触的齿面速度不同引起齿面相对滑动造成的摩擦[9]，其功率损失计算公式为：

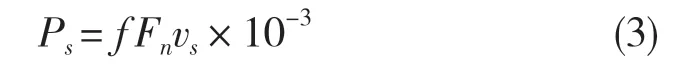
式中：Fn——啮合面法向载荷；vs——齿轮相对滑动速度；f ——滑动摩擦系数。

在齿轮啮合的过程中，不均匀的润滑油膜压力导致齿轮啮合过程中产生滚动摩擦功率损失Pr，其计算公式为[10]：

式中：vr——齿轮相对滚动速度；bb——齿轮有效齿宽；hR——油膜厚度；——主动齿轮分度圆螺旋角。

1.2.3 轴承热功率损失建模

轴承在工作过程中，滚子和滚道间相互摩擦产生热量，其热功率主要受摩擦力矩和旋转速度影响，轴承受到的摩擦力矩包括载荷引起的摩擦力矩和润滑油粘滞引起的摩擦力矩。

变速器采用深沟球轴承，其工作时由载荷引起的摩擦力矩计算公式为[11]：

式中：f1——与轴承结构和载荷有关的系数；Pb——当量动载荷；dm——轴承节圆半径。

轴承在旋转过程中，由于润滑油的粘滞特性使轴承产生旋转摩擦力矩M2，计算公式为：

式中：f2——与轴承结构和润滑方式相关的系数，变速器采用油浴润滑，取f2=2；nb——轴承旋转速度；υ——润滑油运动粘度。

综上得到轴承的摩擦热功率为：

2 电磁直驱变速器传热学热阻分析

由于低温物体向外界辐射的热量较少，本文忽略变速器向外界的热辐射。根据电磁直驱变速器的结构，对内部各部分的导热热阻和对流换热热阻进行分析[12]。

2.1 导热热阻分析

2.1.1 变速器壳体热阻

变速器壳体可视为6 个薄壁平板组成的矩形箱体，每一面薄壁平板的宽度和长度都远大于厚度，可视为一维温度场，即认为薄壁平板温度仅沿厚度方向上变化，忽略平板4 个侧面的边缘散热，其导热热阻为：

式中：δ——壳体厚度；ks——变速器壳体材料热导率（见表1）；A——壳体外表面面积。

2.1.2 轴承与轴及壳体间热阻

在变速器工作时，轴承内滚子与内外滚道相互摩擦产生热量，热量一部分经内滚道传递至齿轮轴，另一部分经外滚道传递至壳体。轴承结构可视为圆筒壁形式，认为其热量仅沿径向传递，属于一维稳态导热，则轴承与轴间的热阻模型为：

轴承与壳体间的热阻模型为：

式中：rbo——轴承滚珠中心半径；rs——轮轴半径；Bb——轴承宽度；rb1——轴承外圈半径；kb——轴承材料热导率，见表1。

2.1.3 齿轮与轴间热阻

为简化计算，将输入齿轮视为齿轮主体和摩擦锥面的2 个圆筒壁结构，由于二者的厚度较小，认为其接触面产生的热量仅沿径向向齿轮轴传递，为一维稳态导热模型，两者的导热热阻为：

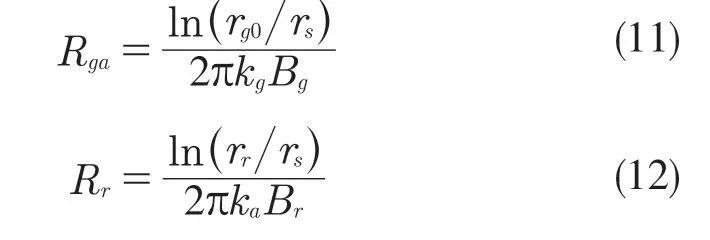
式中：Rga——齿轮与轴导热热阻；Rr——齿轮同步锥面与轴导热热阻；rg0——齿轮节圆半径；rr——同步锥面平均半径；Bg——齿轮宽度；Br——同步锥面宽度；kg——齿轮材料热导率；ka——轴材料热导率，见表1。

表1 各部件尺寸参数及材料热导率Tab.1 Dimensional parameters of components and thermal conductivity of materials

2.2 对流换热热阻分析

2.2.1 齿轮与润滑油间对流换热热阻

变速器在工作时齿轮与润滑油接触形成对流换热，以减少齿轮副的摩擦损失，其对流换热热阻由参数ψ决定：

当ψ<0.68 时，齿轮与润滑油的对流换热热阻为：

当0.68<ψ<1.5 时，齿轮与润滑油的对流换热热阻为：

式中：Dp——齿轮分度圆直径；λ——润滑油导热系数；Dh——齿轮中心到变速器底的高度；Do——润滑油高度；h——齿轮全齿高；τ——齿轮浸入润滑油的时间；m——齿轮模数；Z——齿轮齿数；ωg——齿轮旋转角速度。

2.2.2 轴承与润滑油间对流换热热阻

变速器在工作时，轴承与壳体内润滑油通过对流换热进行散热，其对流换热热阻模型为：

式中：Rbho1——轴承内圈热阻；Rbho2——轴承外圈热阻；Hbho——对流换热系数；ωb——轴承旋转角速度；Pr——普朗特数。

2.2.3 变速器壳体与润滑油间对流换热热阻

变速器内润滑油通过传动系统旋转时产生的回旋力飞溅到变速器壳体内壁，形成两者的对流换热，其对流换热热阻计算模型为：

式中：Ain——变速器壳体内部对流换热面积；Hxho——对应对流换热系数。

2.2.4 变速器壳体与外界空气对流换热热阻

变速器内热量在传递到壳体后，壳体表面温度升高，外表面与空气发生对流换热，形成变速器外壁与空气间的对流换热热阻，计算公式为：

式中：Hxha——变速器壳体与空气间的对流换热系数。

3 电磁直驱变速器热网络模型

热网络法将温度差类比电势差、热阻类比电阻、热流类比电流，基本原理为：将研究对象划分为若干单元节点，将所有网络节点看成具有集总参数的单元，因网络节点之间存在温度梯度，其各节点间必然存在热量传递，节点间的热量传递阻力用热阻表示，形成热网络[13]。

根据电磁直驱变速器的结构，选取关键部件的不同位置进行温度节点划分，具体布置如图3 所示，基于变速器内部热量传递路径，将变速器内主要部件进行节点划分并编号，共划分出39 个温度节点，各温度节点的含义见表2。

表2 变速器各温度节点标注及含义Tab.2 Description and meaning of each temperature node of the gearbox

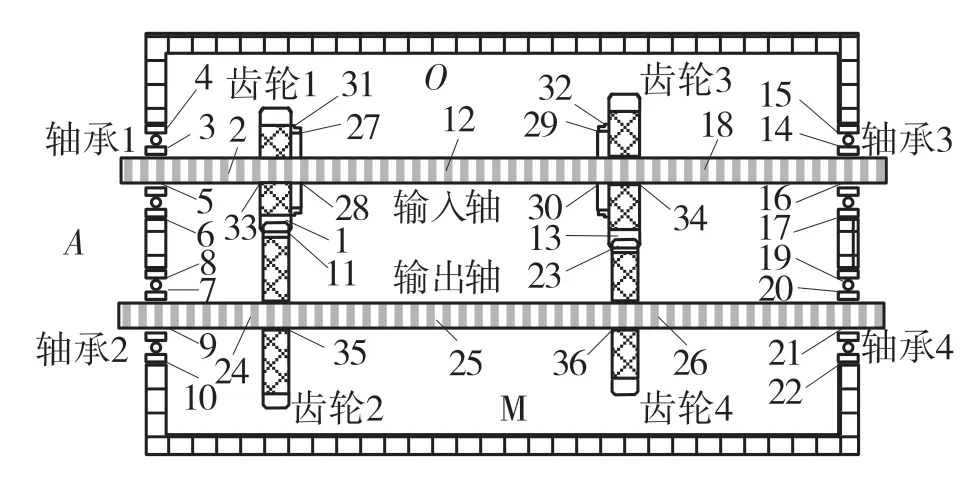
图3 变速器热网络节点划分示意图Fig.3 Schematic diagram of node division of transmission thermal network

根据图3 所示的温度节点标注图，通过热流传递路线将各节点转换成热阻串联起来，建立变速器所对应的热网络图，如图4 所示，图4 中，表示摩擦副摩擦生热热源产生的热量，下标R 表示节点间的热阻，下标C 表示热传导，下标V 表示热对流，●表示节点。

图4 变速器热网络模型Fig.4 Transmission thermal network model

4 热平衡方程求解及结果分析

4.1 热平衡方程及迭代求解

由图4 可知，变速器内部共划分为39 个节点，参照基尔霍夫定律和能量守恒定律，各节点的吸收热量等于放出热量，建立热平衡方程。为简化计算模型，需要进行如下假设：（1）系统所有部件之间的热传递为稳态传热过程；（2）忽略不同部件之间的辐射换热；（3）传热系统各部件材料的热阻大小与热流方向无关。

根据能量守恒定律可知：

式中：Qin——节点吸收热量；ΔQ——节点内能增量；Qout——节点放出热量。

参照能量守恒定律，变速器热网络系统各部件的温度达到稳态前，将吸收或放出热量，其温度随时间变化，温度变化量取决于各部件材料的比热容，节点瞬态温度求解公式为：

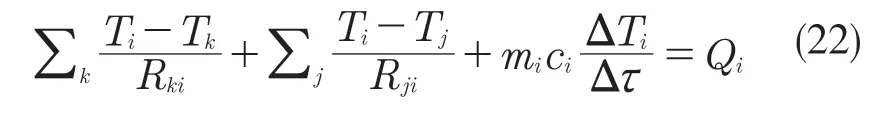
式中：Ti，Tj，Tk——相邻节点的温度；Rij，Rik——节点间的热阻；mi——节点i 的质量；ci——节点i 的比热容；Δτ——时间变化量；Qi——节点i 吸收的热量。

当系统各部件温度达到稳态后，各节点的温度不再随时间变化[14]，即ΔTi/Δτ=0。节点稳态温度求解公式为：

根据图4 的热网络模型图节点温度传递路线，采用矩阵方程进行求解：

式中：[A]n×n——节点温度系数矩阵，即热阻矩阵；[T]n×1——节点温度向量，[T]n×1=(T1，T2，…，Tn)T；[Q]n×1——节点热源向量，[Q]n×1=(Q，Q2，…，Qn)T。

根据上文分析所得变速器各热源的功率损失、各部件对应热阻及边界温度条件，求解式（24）方程组，可得变速器内温度场达到平衡状态时各节点的温度分布情况。因节点较多，采用一阶定常迭代法降低计算难度进行求解，将矩阵A 分解为A=M-N，将式（24）转化为求解方程[M][T]=[N][T]+[Q]，即：

根据上述递推公式可得一组向量序列T(1),T(2)，…，T(n)，设置较小的误差以保证结果的精确，根据式（26）迭代求解可得稳态下各节点的温度值。

4.2 计算结果分析

基于上文模型，在MATLAB 中利用式（26）进行1 阶定常迭代计算，润滑油初始温度为25℃，外界空气初始温度为20℃，得驱动电机最高转速及功率工况下变速器连续换入1 挡5 次后，各节点稳态温度值如表3 所示。计算功率、转速、扭矩不同组合形式的典型工况下电磁直驱变速器各节点温度值，以图形形式表示其温度分布场如图5所示。

表3 节点稳态温度值/℃Tab.3 Node steady state temperature values/℃

从表3 及图5 可以看出，变速器中热源处节点温度明显高于其他节点，其中同步环与换挡齿轮锥面热源节点温度最高，为96 ℃；节点38（空气节点）为最小温度节点，为45 ℃左右；节点3（轴承内圈）温度要高于节点4（轴承外圈）温度，原因在于轴承外圈滚道与轴承滚子生成的热量大部分传递给了变速器壳体，由变速器壳体与变速器外的空气发生对流换热散发到空气当中。在其他条件相同的条件下，随着驱动电机功率和转速的提高，各节点温度也相应提高。值得一提的是，齿轮副和同步环摩擦锥面节点温度会随扭矩的增加明显提高。

图5 不同工况下各节点稳态温度值Fig.5 Steady state temperature values at each node under different operating conditions

5 结论

（1）本文对合作高校课题组提出的电磁直驱变速器内部各热源的发热情况进行了分析，建立了各节点的热阻模型，特别是考虑了同步器与摩擦锥面的发热，在已有研究的基础上更贴近实际；

（2）根据热阻模型建立了变速器热网络模型与内部温升的热平衡方程，并在MATLAB 中采用1阶定常迭代计算出变速器内部各节点稳态温度值，最终得到各节点稳态温度变化情况，分析结果表明：随着驱动电机功率和转速的提高，各节点温度相应提高，各节点中同步器与摩擦锥面间的温度是变速器内部温度最高的区域。如何降低同步器与摩擦锥面温升对换挡品质的影响可进一步研究。