基于深度强化学习的多无人机自主决策算法

丁玮，翟艺伟

（1.中国人民解放军32801 部队，北京 100000；2.中国电子科技集团公司第二十研究所，陕西 西安 710000）

近年来，多无人机协同作战涌现的编队智能表现出巨大的军事潜力。目前，多无人机编队的自主决策算法成为国内外学者的研究热点[1-2]。传统的自主决策算法有人工势场法[3]、Voronoi 算法[4]、模型预测控制算法[5]、A*算法[6]、智能优化算法[7-8]等，这些算法多关注全局信息下的自主决策，但真实的战场环境具有未知性和不确定性。近些年来，深度强化学习的快速发展为无人机自主决策提供了新的解决思路[9-12]，结合深度学习的感知能力和强化学习的决策能力，有望实现在线、动态的无人机自主决策。

通过建立多无人机自主决策问题模型，运用多智能体强化学习的相关知识，对无人机编队的动作进行规划，使之实现在复杂环境下的避障路径规划。

1 多无人机自主决策问题描述

多无人机自主决策问题可以描述为在一定的战场环境内存在静态或者动态的障碍物，无人机的目标是根据自身的传感器信息，从初始任务区域出发，最终到达目标区域。

无人机的二维运动学模型如图1 所示，无人机的位置为(px,py)，速度为(vx,vy)，雷达探测距离为R，雷达探测角度为θr，无人机的航向角为φu。无人机在飞行过程中需要躲避的区域建模为图1 所示的半径为Robs的圆形。

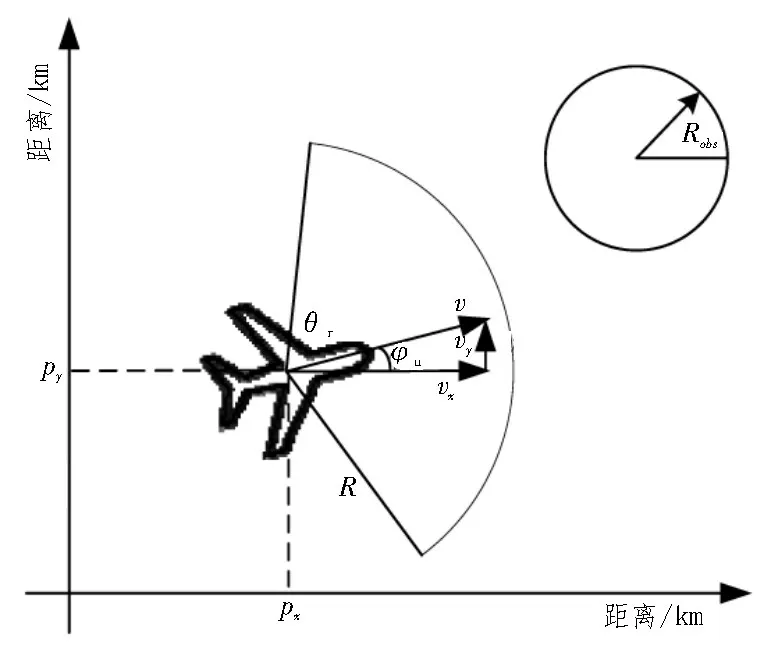
图1 无人机二维运动模型

2 深度强化学习算法

2.1 马尔可夫过程与求解

强化学习的基本过程如图2 所示，环境的状态因为智能体决策的动作发生改变，同时，智能体接受环境对于动作优劣的判断[13-15]。

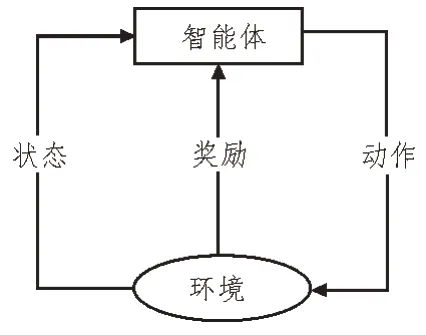
图2 强化学习基本过程

马尔可夫决策过程的目标就是寻找一个最优策略π，使得智能体的累计回报值最大。在马尔可夫决策过程中，状态价值函数vπ(s)和动作价值函数qπ(s,a)定义如下：

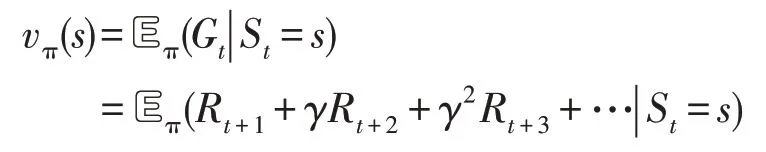
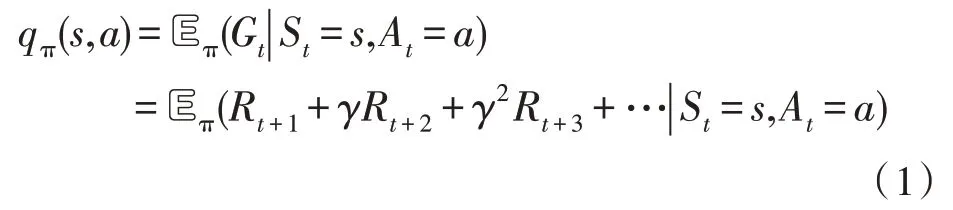
其中，Gt代表累计回报。

时间差分方法[16]是应用最广的强化学习算法，SARSA 算法和Q-learning 算法是其中的两种代表性算法。SARSA 算法也是一种在线策略（on-policy）算法，其动作价值函数的更新公式为：

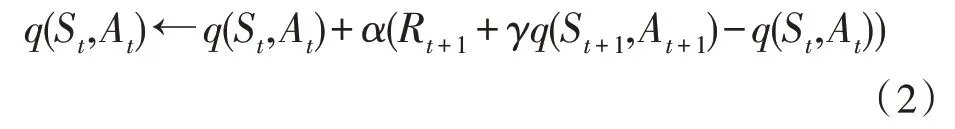
其中，α代表学习速率。

Q-learning 则是一种离线策略（off-policy）算法，它的动作价值函数更新公式为：

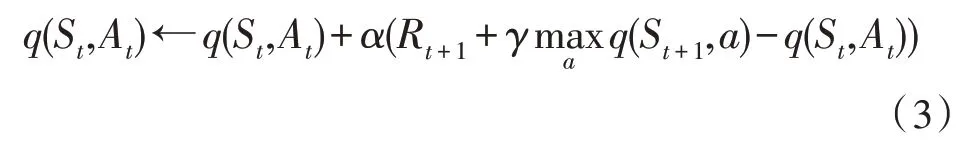
2.2 深度确定性策略梯度算法

深度确定性策略梯度（DDPG）算法[17]借鉴了DQN算法[18]的经验回放机制和双网络结构，同时利用确定性梯度的特点，通过Actor 网络直接输出具体的动作，使其能够应用在高维的动作空间。DDPG 算法采用Actor-Critic 算法框架，其算法框架如图3 所示。

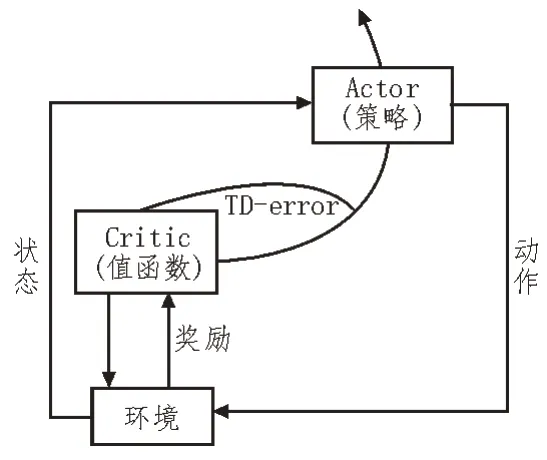
图3 Actor-Critic算法框架

具体地，DDPG 算法设计了四种网络，即Actor 当前网络、Actor 目标网络、Critic 当前网络和Critic 目标网络。其中，Actor 当前网络和Critic 当前网络的参数更新公式如下：

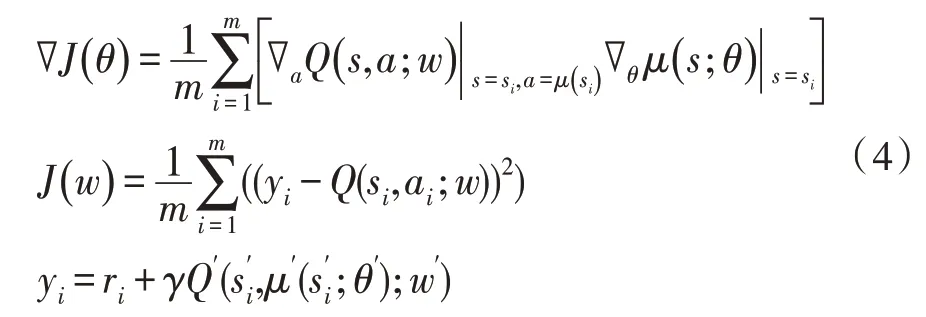
其中，θ是Actor 当前网络的参数，θ′是Actor 目标网络的参数，w是Critic 当前网络的参数，w′是Critic 目标网络的参数，Actor 当前网络输出的确定性动作为a=μ(s;θ)，m是经验池中随机采样的数据总数，yi是目标Q值。

Actor 目标网络和Critic 目标网络的参数通过软更新的方式进行更新，使得算法更加稳定。

2.3 MADDPG算法

由于DDPG 算法应用于多智能体时无法利用全局智能体的状态信息，因此，Critic 网络给出的状态值函数并不十分准确，同时算法的稳定性会受到智能体之间的影响。为了解决这些问题，文献[19]提出了多智能体深度确定性策略梯度（MADDPG）算法。

MADDPG 算法的Actor 网络结构只考虑单个智能体的局部状态信息，但是Critic 网络结构考虑了其他智能体的状态和动作信息。

对于MADDPG 算法，第i个智能体的策略梯度公式可以表示为式（5）：

其中，θi是第i个智能体Actor当前网络的参数。

第i个智能体的Critic 网络参数更新可以表示为式（6）-（7）：

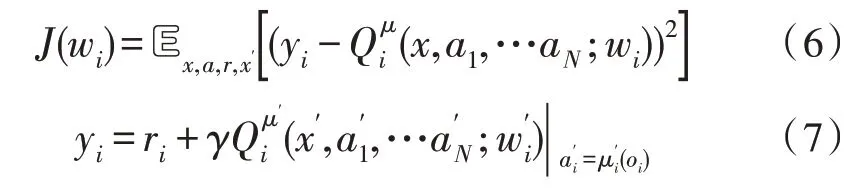
其中，ai代表第i个智能体的动作，wi是第i个智能体Critic 当前网络的参数，是第i个智能体Critic 目标网络的参数，yi代表目标Q值。

3 多无人机自主决策问题建模

多无人机自主决策问题可以描述为在有限任务区域中，无人机躲避环境中的障碍物，最终到达各自的任务区域。如图4 所示，多无人机自主决策环境中包含无人机、目标和障碍物。其中，是无人机的位置坐标，是目标中心点的位置坐标，是障碍物中心点的位置坐标。

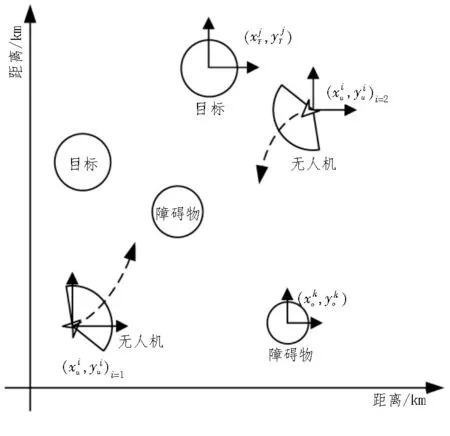
图4 多无人机自主决策环境

多无人机自主决策问题中的状态空间、动作空间和回报函数可表示如下。

第i架无人机的状态信息由无人机速度、位置、无人机相对目标的距离、无人机相对其他无人机的距离、无人机相对障碍物的距离组成。具体可表示为。

无人机的动作空间由各个方向的外力表示，第i架无人机的动作空间可以表征为。

为了避免稀疏回报问题，将多无人机自主决策的回报函数表示为式（8）：

其中，dis(·)表示二维空间中的欧式距离，Rt是目标半径，Ro是障碍物半径，Ru是无人机碰撞距离。r1是无人机到达目标区域获得的奖励值，r2是任务失败的奖励值，包括无人机发生碰撞、无人机进入障碍物区域，rdis是无人机与目标的距离带来的奖励项，robs是无人机与障碍物的距离带来的奖励项。

4 仿真实验与分析

4.1 实验参数设置

在实验中，DDPG 算法和MADDPG 算法的Critic网络结构有所区分，DDPG 算法的Critic 网络输入局部状态观测值和动作值，MADDPG 算法的Critic 网络则输入所有智能体的状态观测值和动作值。

算法中的其他参数设置如下：每一回合的最大长度为400，学习率为0.001，折扣因子为0.95，经验池的大小为1×106，批量训练集大小为1 024，目标网络的更新率τ=0.01。

4.2 实验对比与分析

回合平均回报值（Episode Average Return，EAR）是智能体在有限回合所获得的奖励值，收敛时奖励值越高，说明算法越具有优势，具体如式（9）：

式中，N表示有限回合的个数，|En|代表第n个回合的长度，无人机的数量为Nu，r(ui,j)表示无人机在第j步的奖励值。

在有15个障碍物的自主决策环境中，利用DDPG算法和MADDPG 算法对无人机编队进行训练，学习过程中的回合平均回报值的变化如图5 所示。

图5 多无人机自主决策训练过程

图5 横坐标代表训练的回合数，纵坐标代表回合平均回报值。分析图5，由于训练过程中存在随机噪声，算法呈现一定的震荡，但两种算法在训练一段时间后均呈收敛趋势，不过两种算法收敛的速度和时间存在一些差异。相比之下，MADDPG 算法比DDPG 算法更早的收敛，且收敛后的回报值高于DDPG算法。

为了测试算法收敛后的性能，分别利用训练完成的两种算法模型在障碍物数量为0 个、8 个、15 个的环境中，对多无人机自主决策能力进行测试。测试任务成功率如图6 所示，在不同密度的障碍物测试环境中，MADDPG 算法能取得比DDPG 算法更高的成功率。

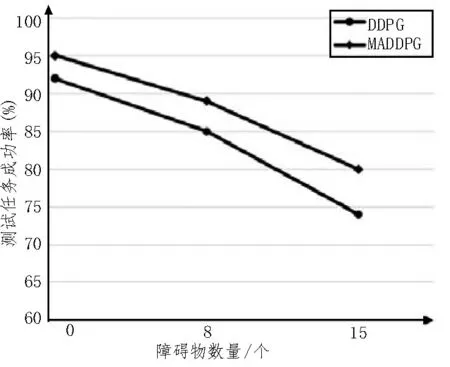
图6 测试任务成功率

5 结束语

以多无人机自主决策为研究背景，构建了多无人机自主决策环境，通过描述马尔科夫决策过程，分析了深度确定性策略梯队算法和MADDPG 算法。仿真实验结果验证了应用在多智能体领域的MADDPG 算法能有效地对多无人机进行路径规划，在有障碍环境中实现自主决策。随着多智能体数量的增多，MADDPG 算法将难以收敛，如何改进算法网络，提高采样效率，值得进一步地开展研究。