基于遗传算法的分数阶锂电池模型参数辨识

吴俊，杨维明，姚静，黄秋安

(1.湖北大学计算机与信息工程学院， 湖北 武汉 430062; 2.上海大学可持续能源研究院， 上海 200444)

0 引言

锂离子电池由于其能量密度高，使用寿命长，记忆效应低等特点，通常被用于便携式电子设备(如手机、蓝牙耳机)和电动汽车等领域[1-2]，并且在军事和航空航天应用中日益流行.锂离子电池在其充放电过程中，锂离子在正负电极上完成脱嵌和嵌入，在电解质中完成转移.由于传统锂电池使用液体电解质，而液体电解质具有易燃、易爆、易挥发的特性，在受到外部撞击或者其他极端情况时，会发生电池短路，继而起火燃烧，无法提供足够的安全保障.最近的特斯拉汽车起火事件表明，必须对电池的运行状态进行监控和管理.

单纯使用SOCSOH等外特性参数描述电池，不足以揭示电池运行状态.尤其不足以探究电池电气特性的变化，当电池内阻变得很大时，根据焦耳定律，容易造成电池局部过热，进而导致电池爆炸起火等重大安全事故.因此，要完成对电池运行状态的监控管理，必须对电池的阻抗特性进行描述.

本文中主要工作是选用分数阶模型作为锂电池的等效电路，主要完成三个工作：1)利用分数阶定义，给出该分数阶模型的任意序列输入条件下的数值解；2)完成在该模型框架下的阶跃响应；3)利用遗传算法完成对该模型电路参数的辨识仿真，并分析其误差.

1 分数阶理论及改进Randle模型的参数提取

分数阶理论有三种定义，这里仅介绍一种常用的数值逼近方法，即Grüwald-Letnikov，简称GL定义.假设函数满足处处连续且可导条件，根据整数阶的Hospital法则，可扩展得到其分数阶的导数定义为[3-5]：

(1)

说明如下：

1)「⎤表示向上取整，h表示步长，类似整数阶导数分母，越小越好，α表示分数阶阶数；

2)t0表示时间起点，即在该定义下，当前函数值涉及从t0开始到t之间所有时间点的函数值；

GL定义下，其分数阶积分的拉氏变换见公式(2)：

(2)

在经典等效电路模型中，一阶RC模型试图模拟欧姆电阻和电荷转移反应，对应于高频尾线和低频直线，但没有描述中频范围内的扩散行为.对于二阶RC模型，可以模拟欧姆电阻和扩散行为，但不能考虑电荷转移过程.Yu Zhihao等[6]使用第三阶或更高阶的RC串联模型，所有三个过程都可以产生.然而，这些模型有大量的参数，不仅使与计算负担相关的模型数学结构复杂化，还增加系统校准的工作量和过拟合的风险.此外，正如Westerhoff等[7]所证明的，即使使用5个RC串联网络，该模型也不能非常准确地捕捉零相位.

为了解决上述问题，分数阶微积分(FOC)最近被用于锂离子电池的建模，Wang J L等[8]用CPE单元替换一阶RC模型并联块中的理想电容器，得到分数阶模型.这些分数阶等效电路模型可能包含一个或多个CPE元件.通过简单地将一阶RC模型中的理想电容替换为分数阶单元，得到的分数阶模型FOM，如图1所示.利用分数阶导数，发现该模型对实验数据的拟合有较好的精度，该分数阶模型的阻抗表达式为：

Z(s)=R0+Zct(s)+Zd(s)

(3)

说明如下：

1)R0表示电解质的欧姆电阻和连接电阻；

2)Zct(s)表示电荷转移电阻，通常由一个电阻Rp与CPE并联组成，其中CPE表示电解质和电极表面形成的非理想电容，也称为常相位单元[9-11]；

3)Zd(s)表示锂离子在低频条件下的扩散电阻，被称为Warburg阻抗.

常相位单元CPE的频域表达式为：CPE(s)=1/Q1sα.其中，Q1是一个常数，量纲是F·s1-α；α∈(0,1]表示非理想电容的分数阶阶数，当α=1时，CPE就退化成标准电容，这里τ=(RpQ1)-α，公式(3)中的电荷转移电阻可表示为：

(4)

对于阻抗谱的实际测量，频率范围通常受到测试设备和物体特性的限制.因此有效的频率范围一般设置为:(100 mHz,100 kHz).本文中着重讨论实际应用情况下，半无限扩散条件下的Warburg阻抗，即：

(5)

待辨识参数为：θ={R0,Rp,Q1,α,Q2}.

2 改进Randle模型下的分数阶响应

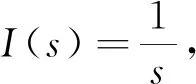
(6)

此时，除了上面提到的利用定义法求解分数阶响应外，还可以借助文献[12-13]，利用反拉普拉斯变换，给出该阶跃响应的解析解，见公式(7)～(8)，这里的α∈(0,1].文献[12-13]中已经证明，该解析解与定义法等价.

(7)

(8)

如图2为改进Randle模型下的阶跃响应.阶跃电流为1 A，横轴表示时间，纵轴表示响应电压，参数θ={7.37,6.243 ,3.073 ,0.782 ,608.1}，即参照下文中表1中的预设参数θ值取值.

3 参数辨识及其结果分析

辨识的基本步骤包括实验设计、数据采集、数据预处理、结构辨识、参数估计、模型验证等.实验设计主要包括激励信号的选择，采样周期的确定，激励信号数据长度，离线辨识还是在线辨识等，主要目的是使采集的输入输出数据尽可能多地包涵系统的内在特性.因此，本仿真实验采用阶跃电流和正弦电流作激励，希望尽可能与实际获得的实验数据相仿或相近.

参数辨识方法有很多，从信号的实时性看，可以分为两大类，一是在线辨识，二是离线辨识.本文中采用离线辨识方法，利用遗传算法，作参数优化，得到最终的参数辨识结果.实际上除了一次完成算法外，其他无论哪种方法，其辨识流程大体均如图3所示.

如果用θ表示分数阶系统的参数，用F(θ)表示待辨识模型的数学映射，当输入电流为i(t)时，可以得到辨识模型计算值um和锂电池模型的响应电压值u，计算目标函数Jθ的值：

Jθ=(u-um)2

(9)

更新并调整参数θ的值，使得目标函数Jθ朝变小的方向靠近，当输出误差函数小到某一指定精度ε，如当Jθ<ε时即认为辨识成功.可认为在指定精度ε下，可以用辨识模型代替锂电池系统.

3.1 遗传算法原理遗传算法[14-16]是美国教授John Hollond于上世纪60年代提出的一种受自然选择过程启发的元启发式算法，属于进化智能算法的一种，通常依赖于生物启发的算子，如选择、交叉、变异等生成高质量的优化和搜索问题的解决方案.遗传算法本质上是一种基于达尔文的“物竞天择、适者生存”原则的仿生算法.目标生物种群在捕食者和环境危害威胁等外在条件下，不能适应的弱小生物个体被消灭，更能适应生存环境的优秀个体被保留.通过优胜劣汰筛选后的生物成员往往比其他成员有更好的生存机会.它们更有可能适应进化条件，它们产生的后代可能会遗传并继承他们的特征，学习和模仿它们的技能，从而产生更健康的后代.此外，基因突变在物种成员中随机发生，其中一些突变可能会提高健康个体及其进化后代长期存活的机会.最后存活下来得到的个体就是优化问题的最优解.

标准遗传算法从随机生成的可能解群体(个体)开始.首先计算个体的适应度，根据个体的适应度值选择部分个体作为父母，产生父群体.通过将交叉算子应用于父群体，然后将变异算子应用于它们的后代，产生了可能解的新群体(子群体).重复用新子代替换双亲(旧个体)进行迭代，直到满足停止标准.

本文中采用遗传算法的流程图如图4所示.首先定义电池参数θ，随机生成满足要求的初始种群，计算初始种群的目标函数值，通过遗传算子(选择、交叉、变异)得到新的候选解种群，重复计算新种群中目标函数的值.当某个体目标函数值小于指定精度时，停止迭代，该个体即为最优个体输出，否则继续迭代.需要注意目标函数值与适应度一一对应，目标函数需要作适应度转换，才能输出该个体的适应度.

3.2 辨识结果分析本文中采用遗传算法作为辨识算法，为了验证辨识算法的有效性，假定电池的既定参数如表头所示，在激励电流为阶跃信号输入的条件下，使用遗传算法，取较好的4次结果展示在表1中.由于遗传算法的收敛结果有一定波动性，每次运行结果都不尽相同，因此表中仅列出4组辨识结果.如表1中误差均值MAE所示，每个点对应的误差均值精度达10-5，比原数据高出2个数量级，结果正确有效.

图5是改进Randle分数阶模型辨识结果(表1)的阶跃响应图，横轴是时间，纵轴是响应电压.其中图5(a)是激励时长为0 ～ 100 s的阶跃电流在4次参数辨识结果下的阶跃响应.从图5(a)的拟合效果看，4次辨识结果的拟合值基本与预设值响应结果重合，拟合程度也“较好”.图5(b)是对图5(a)中从35 ～ 80 s时间片段(蓝色虚线框部分)的局部放大.从图5(b)可看出，除了“2#”外，其他3次辨识结果拟合曲线与预设值“完全重合”，拟合程度较高.

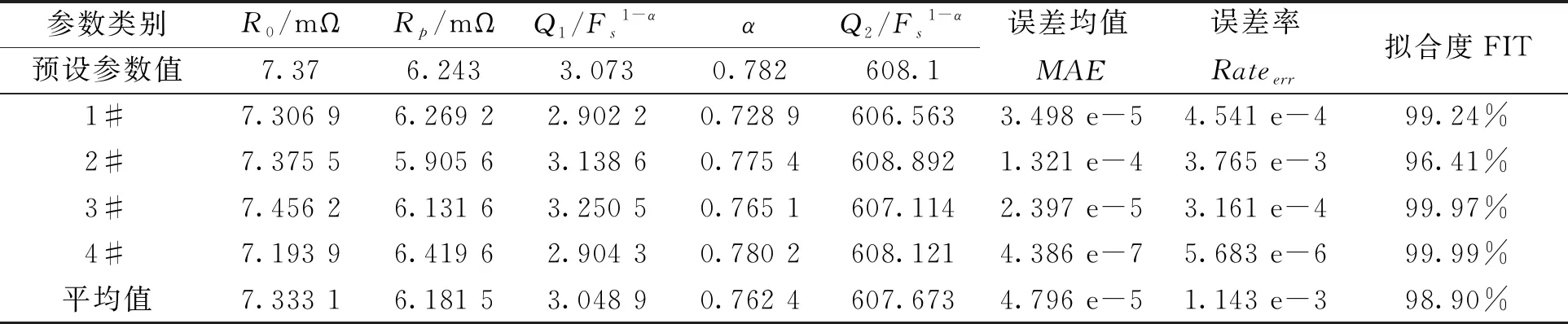
表1 阶跃响应辨识结果

图6是“2#”个体遗传进化过程图，即给出了“2#”遗传算法优化过程的实验结果，横轴是遗传算法执行代数，纵轴是适应度值.由于响应电压的幅度值相对较小，在每个点上仅存在10-5的误差，因此，需要进行适应度变换，这里使用公式ObiV=log(∑(u-um)2)作为适应度函数.由于本身电阻较小，扩散系数很大，导致电压在10-3量级，因此在图5(b)的微观尺度上显示出很大的差距.从实际的误差均值上可看出，拟合后的响应电压与电压真值之间差距很小.遗传进化过程图(图6)显示，遗传到180代时，ObiV已经小到-11个量级，说明均方误差函数也已达到10-11，可以认为对模型而言，已经达到较好的精度，也进一步验证图5(b)中，看起来的差距很大的图，实际并不大.

4 结论

本文中主要研究动力锂离子电池的改进Randle模型，讨论该模型在输入信号为阶跃电流情况下的解析解，并给出其阶跃电压响应曲线，实现对该模型在阶跃激励下模型参数的提取.在此基础上，利用遗传算法对该系统模型的参数完成辨识，参数辨识误差均值接近10-5，拟合程度在98%以上.