奇长度的4q-QAM互补序列集
丁小茂,周亚晶,罗荣
(西南交通大学数学学院, 四川 成都 611756)
0 引言
格雷互补序列(Golay complementary sequences,GCS)可用于OFDM信号产生低PMEPR波形. 1999年,Davis-Jedwab[1]基于广义布尔函数构造了多相GCS[2],产生的OFDM波形PMEPR最大为2[2-3]. Paterson[4]基于RM码推广了Davis-Jedwab的成果. Schmidt[5]将Paterson的构造扩展到广义RM码的高阶陪集,获得了更高的码率. 上述文献中基于广义布尔函数构造的GCS的长度都是2的方幂. Chen[6-7]基于广义布尔函数构造了长度为非二方幂的q元(q为偶数)互补序列集,其PMEPR为集合大小的上界.
上述互补序列为多相互补序列,QAM互补序列由于其较大的码率而广泛应用于OFDM系统. 基于两个四元GCS的组合,Röβing-Tarokh[8]首次从加权和中构造了最大PMEPR为3.6的16-QAM GCS序列. 结果表明,该序列的码率是PMEPR略高的多相GCS的两倍. 后来,Chong-Venkataramani-Tarokh[9]利用广义布尔函数推广了他们的结果. 在文献[9]中,作者发现,在相同的PMEPR约束下,具有16-QAM GCS的OFDM系统比仅具有二元或四元GCS的OFDM系统更能得到较高码率. 后来学者们又给出64-QAM GCS的一般性构造[10-11]. Li[12]修正了文献[9]中的序列对描述、文献[11]中给出的构造. Li[13]给出3类4q-QAM (q≥1) GCS构造. Liu-Li -Guan[14]利用高斯整数对,构造了2类新的4q-QAM (q≥3) GCS. 在文献[15]中,Zhou- Zhou -Yang利用广义布尔函数构造出长度为2m-1+2v(1≤v≤m-2)的4q-QAM (q≥1) CSS. 事实上,利用广义布尔函数构造的4q-QAM CSS多为偶长度,但关于奇长度的4q-QAM (q≥1) CSS研究相对较少,本文中的研究动机就是设计奇长度的4q-QAM CSS. 受文献[13]和[6]中工作的启发,本研究构造了奇长度的4q-QAM CSS,确定了新序列数目,并给出了新序列PMEPR的上界.
1 预备知识
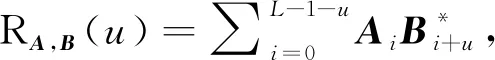

(1)
令n为正整数,n={0,1,…,n-1}表示整数模n后形成的集合.对于广义布尔函数为从{0,1}m到n的一个映射. 给定定义f=(f0,f1,…,f2m-1),其中fi=f(i1,i2,…,im),(i1,i2,…,im)表示i的二进制表达相应系数,即其中im表示最高位系数.
本研究考虑上述f的截断. 令f(L)为f去掉最后2m-L个元素,形成L长的序列.取ξ为n次单位复根. 定义长度为L的复值序列ψ(f)(L)由f(L)生成:ψ(f)(L)=(ξf0,ξf1,…,ξfL-1).为了简洁,将忽略f(L)的上标.
Li[13]中提出了一种4q-QAM GCP的构造方法.
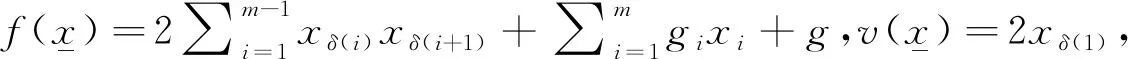
2 奇长度4q-QAM CSS的构造
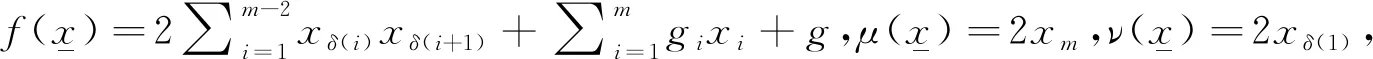
E=(E0,E1,…,EL-1),F=(F0,F1,…,FL-1),G=(G0,G1,…,GL-1),H=(H0,H1,…,HL-1),
为证明定理2,需要用到文献[6]和文献[1]中的两个定理. 下面将给出这两个定理.
定理3[6]各符号含义与定理2一致,则集合{ψ(A(L)),ψ(B(L)),ψ(C(L)),ψ(D(L))}为长为L的互补序列集.
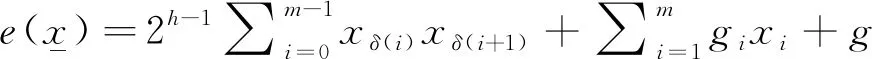
下面对定理2进行证明.
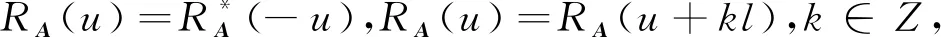
由定理3可知,{ψ(a(p)),ψ(b(p)),ψ(c(p)),ψ(d(p))}(0≤p≤q-1)是一个长度为L的CSS. 因此可以得到Rψ(a(p))(u)+Rψ(b(p))(u)+Rψ(c(p))(u)+Rψ(d(p))(u)=0.从而有
RE(u)+RF(u)+RG(u)+RH(u)=∑p′≠p″rp′rp″[Rψ(a(p′)),ψ(a(p″))(u)+Rψ(a(p″)),ψ(a(p′))(u)
+Rψ(b(p′)),ψ(b(p″))(u)+Rψ(b(p″)),ψ(b(p′))(u)+Rψ(c(p′)),ψ(c(p″))(u)+Rψ(c(p″)),ψ(c(p′))(u)
+Rψ(d(p′)),ψ(d(p″))(u)+Rψ(d(p″)),ψ(d(p′))(u)]
(2)
Rψ(a(p′)),ψ(a(p″))(u)+Rψ(b(p′)),ψ(b(p″))(u)+Rψ(c(p′)),ψ(c(p″))(u)+Rψ(d(p′)),ψ(d(p″))(u)+
Rψ(a(p″)),ψ(a(p′))(u)+Rψ(b(p″)),ψ(b(p′))(u)+Rψ(c(p″)),ψ(c(p′))(u)+Rψ(d(p″)),ψ(d(p′))(u)=0.
因此,我们仅证明下述等式即可
(3)
其中,
并且
要证明等式(3),可对2m-1≤u 情形1u=2m-1.由2(im-jm)≡2 (mod 4)可得 故等式(3)成立. 情形2 0 (4) 再证明上述方程右边等于0即可. 先证 (5) 由jm=im=0,由定理1可知:{E,G}和{F,H}皆是长为2m-1的4q-QAM格雷互补对. 再由定理4可知:对所有0≤p≤q-1,{ψ(a(p)),ψ(c(p))},{ψ(b(p)),ψ(d(p))}都是长为2m-1的格雷互补对. 综上,对所有0≤p′≠p″≤q-1,可得 从而等式(5)成立. 再证 (6) 由于2(jm-im)≡2 (mod 4),因此有 从而得到等式(6). 根据上述分析可知,对所有1≤u 一般来说,要得到定理2所生成序列的精确PMEPR是很难的. 然而,基于Liu-Guan[16]的研究结果,这些序列的PMEPR上界为N.根据等式(1),可以得到下述结果. 推论1定理2中集合{E,F,G,H}的PMEPR上界为4. 推论1的证明对任意0 于是容易得到 结论得证. 表1给出了大小为4,长度在5和12之间的4q-QAM GCP和4q-QAM CSS. “√”表示对应的序列是存在的. 下述结果表明,定理2所提出的序列参数具有更强的灵活性. 从表2中可以看出,与其他构造相比,只有定理2能得到集合大小为4长度为奇数的4q-QAM CSS. 表2比较了文献[13-15]和本文中构造QAM互补序列的参数. 可以看出,本文中构造的序列弥补了现有参数的不足. 表1 不同长度的4q-QAM GCP和4q-QAM CSS对比 表2 QAM GSS的已知参数对比 本研究在广义布尔函数的基础上,构造了一个大小为4的奇长度CSS. 构造的4q-QAM CSS的PMEPR是有界的. 并与文献[13-15]中的4q-QAM 格雷序列的相关参数进行了比较. 结果表明,所提出的序列参数是新的,为通信系统提供了更多的选择.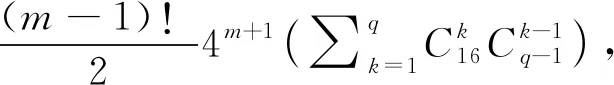


3 结论

