面向骨折手术的三支链六自由度并联机构设计

王 蕊，霍欣明，连宾宾，宋轶民，孙 涛

面向骨折手术的三支链六自由度并联机构设计

王 蕊，霍欣明，连宾宾，宋轶民，孙 涛

(天津大学机构理论与装备设计教育部重点实验室，天津 300350)

随着微创技术和生物学固定技术的发展，创伤骨折手术中愈加需要术中精准定位，以确保内固定物能够精确和微创地固定骨折断端．其中，利用六自由度并联机构进行骨折断端的复位和固定是实现微创精准骨折手术的重要手段，也是未来骨折手术的发展趋势．现有的由6条支链构成的六自由度并联机构存在质量大、医学影像设备扫描后伪影严重等系列问题，提出和设计少支链六自由度并联机构成为研究热点．本文借助有限旋量理论构型综合出一类三支链六自由度并联机构，并进行了其拓扑结构和运动学性能设计．首先，利用有限旋量描述六自由度并联机构及其支链末端的运动，通过有限旋量理论的结合定律和交换定律获得可行支链的标准型和衍生型，通过定义支链装配条件和配置驱动关节，综合出一类三支链六自由度并联机构；然后，定义了优选准则，借助瞬时旋量理论对优选出的5种三支链六自由度并联机构进行了位置逆解、工作空间和速度分析；最后，以运动/力传递率在给定工作空间内的均值与方差为目标函数，考虑并联机构的拓扑结构对运动学性能的影响因素，开展了三支链六自由度并联机构的拓扑结构与运动学性能的一体化设计．上述工作为后续三支链六自由度并联机构的物理样机建造与实验研究提供了理论基础．

三支链六自由度并联机构；有限限量；瞬时旋量；构型综合；运动学设计

随着经济社会发展、人口老龄化加剧、交通运输规模膨胀等多种因素的交叉影响[1]，创伤性骨折疾病频繁发生，日趋成为影响人类生命和健康的突出问题．骨折断端的复位和固定是骨折手术的核心内容，传统的闭合复位和石膏固定方式，复位精度差，仅适用于简单骨折；而切开复位和髓内钉固定方式，复位精度高，可适用于复杂骨折，但创伤大，会导致畸形或延迟愈合等系列问题[2]．

在机器人学与骨科医学的交叉融合中，微创外科手术技术在创伤性骨折治疗中被广泛应用．其中，外固定支架技术无需手术切开创面，仅利用克氏针[3]将两个骨折断端分别与外固定支架的两个平台固结，通过调节平台间支链的长度可使两个平台进行相对运动，从而实现骨折断端的复位．外固定支架技术始于20世纪90年代，前苏联学者G. A. Ilizarov在自行车车轮结构的启发下，发明了由2个钢环与3根螺纹杆组成的Ilizarov外固定支架[4]，但其仅能调整骨折断端沿着骨轴线移动和绕着垂直骨轴线转动的相对调整．1994年，美国骨科医生J. Charles Taylor和工程师S. Harold Taylor将Stewart六自由度并联机构引入骨科，设计出Taylor外固定支架[5]．该支架通过调整6条支链的长度可实现2个平台的六自由度运动，进而实现骨折的精准复位．2006年，通过对Taylor支架的支链与钢环间连接铰链的创新，意大利Ortho-fix公司推出了可实现支链与钢环间快速拆装的Ortho-fix外固定支架[6]．2008年，俄罗斯Ortho-SUV公司推出了新型Ortho-SUV外固定支架[7]，与Taylor支架相比，其刚度和精度更高．综上所述，现有的Taylor、Ortho-fix、Ortho-SUV等支架均由6条支链和2个钢环构成，过多的支链导致外固定支架整体质量较大，且在CT扫描时遮挡/干扰骨折断端造成伪影，增加了骨折断端位姿测量的难度．

因此，为降低支架质量和减少CT扫描时遮挡/干扰骨折断端造成伪影，发明和设计少支链六自由度外固定并联支架是一种较为可行的解决方案．

现有的并联机构构型综合方法可大致分为基于瞬时运动和基于连续运动的方法．基于瞬时运动的方法主要包括约束旋量综合法[8-9]和微分几何综合法[10]，该方法综合出的机构需要进行运动全周期性判断[11]．基于连续运动的方法主要包括位移子群/子流群综合法[12-13]，该方法的相关运算规则过多，数学方法较复杂．Sun等[14-16]提出了有限瞬时旋量方法，可进行机构拓扑的解析表征和代数运算，实现了机构拓扑的代数化综合．对少支链多自由度(如三支链六自由度)并联机构构型综合的相对研究较少．

运动学设计的关键是选择合适的性能评价指标．其中雅克比矩阵的代数特征值(如行列式、条件数和奇异值等)[17-19]常作为机构运动学性能的重要指标．但对于平转耦合机构，雅克比矩阵代数特征值应用于优化设计会产生量纲不统一的问题．另一种方法是通过建立关节速度与输出刚体上若干点的速度映射关系得到具有齐次量纲的雅克比矩阵[20]．该方法得到的性能指标在不同坐标系下描述会有不同结果．另一种利用力旋量与运动旋量的互易积具有与坐标系无关的特点，构造了多种量纲为1且与坐标系无关的运动学性能评价指标．如刘辛军等[21]提出输入、输出及约束传递率指标用于评价机构力和运动的传递特性．现有运动学设计主要针对给定构型，较少考虑不同拓扑构型与运动学性能的综合设计．

针对上述问题，本文综合出一类三支链六自由度并联机构，并进行了其拓扑结构和运动学性能设计.第1节，利用有限旋量描述六自由度并联机构及其支链末端的运动，通过有限旋量的结合定律和交换定律获得可行支链的标准型和衍生型，通过定义支链装配条件和配置驱动关节，优选出5种三支链六自由度并联机构．第2节，对优选出的5种并联机构进行了位置逆解、工作空间和速度分析．第3节，以运动/力传递率在给定工作空间内的均值与方差为目标函数，考虑拓扑结构对运动学性能的影响因素，开展了三支链六自由度并联机构的拓扑与运动性能一体化设计．

1 三支链六自由度并联机构构型综合

1.1 并联机构构型综合流程与期望运动表征

本文以有限旋量[16]作为数学工具，提出了一种三支链六自由度并联机构构型综合方法，其基本流程如图1所示．

图1 基于有限旋量理论的并联机构构型综合

本文六自由度并联机构的末端期望运动为三转动自由度(3R)和三平动自由度(3T)，利用有限旋量的旋量三角积运算可表示为

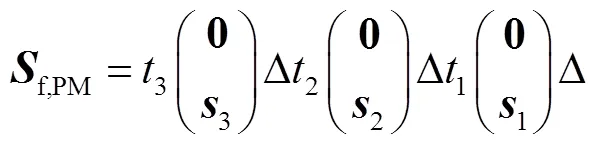
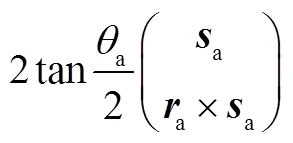
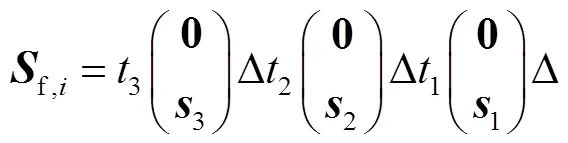
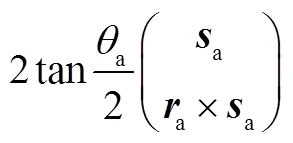
1.2 衍生支链构型综合

在六自由度并联机构标准支链的基础上，可通过运动副类型替换和运动副位置变换两种方式综合更多可行的衍生支链．

运动副类型替换：替换六自由度并联机构标准支链中若干移动副，使所得衍生支链与标准支链的有限运动等价．其中，单自由度平动(1T)由1个移动副或由2个轴线平行的转动副生成，可表示为

运动副位置变换：改变支链中运动副的次序，可衍生出更多可行的支链．利用有限旋量三角积的结合和交换律[20]，变换支链中移动副次序表示为

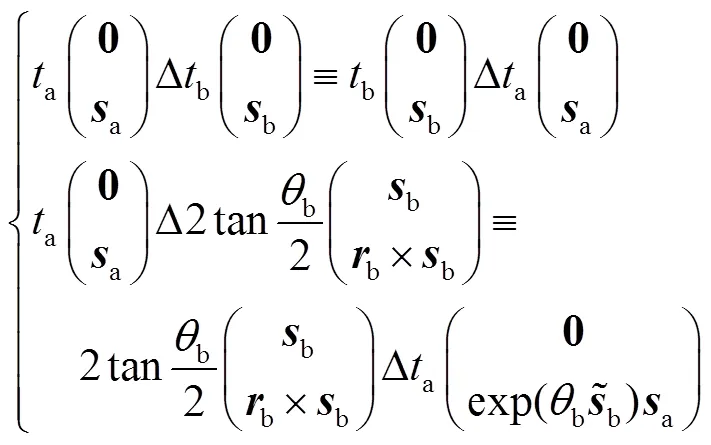
本文根据衍生支链中移动副数目的不同，将衍生支链分为具有0个、1个、2个和3个移动副的4种形式．

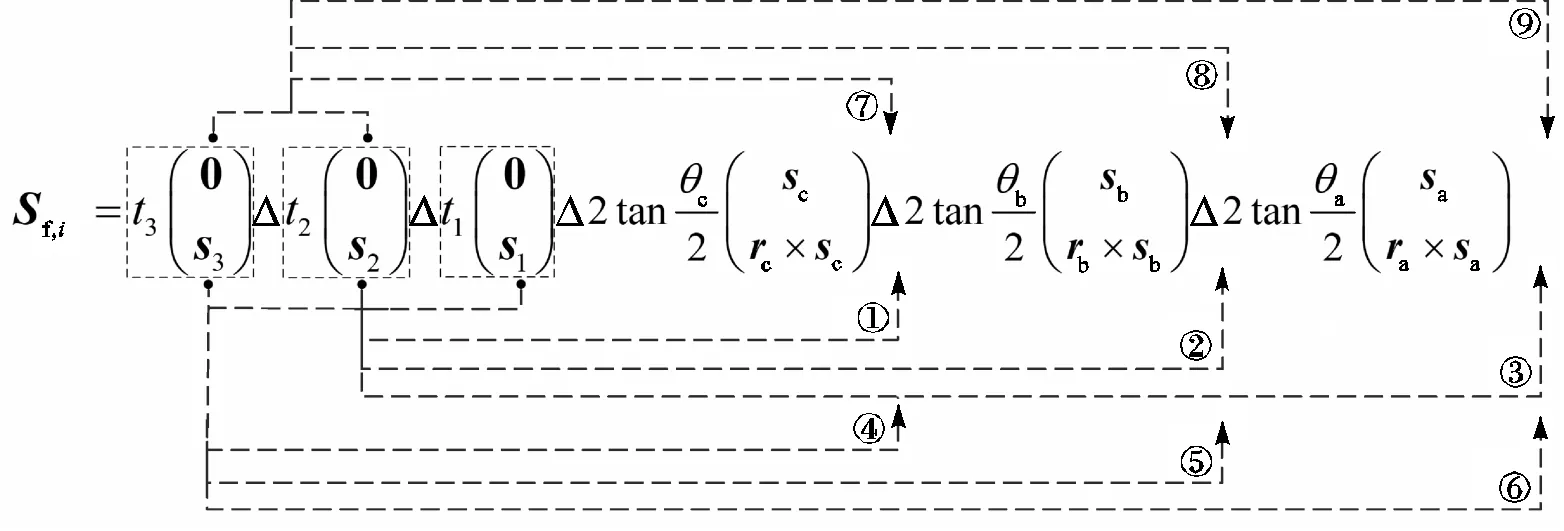
类型Ⅰ：支链中具有3个移动副．

根据式(5)变换标准支链中移动副位置，通过有限旋量的结合和交换律，如式(6)共获得9种衍生支链P2P1RcP3RbRa、P2P1RcRbP3Ra、P2P1RcRbRaP3、P1RcP3P2RbRa、P1RcRbP3P2Ra、P1RcRbRaP3P2、RcP3P2P1RbRa、RcRbP3P2P1Ra、RcRbRaP3P2P1．

类型Ⅱ：支链中具有2个移动副．

基于运动副类型替换，将上述六自由度并联机构的标准支链中1个移动副替换为转动副，由式(4)做等价变换得

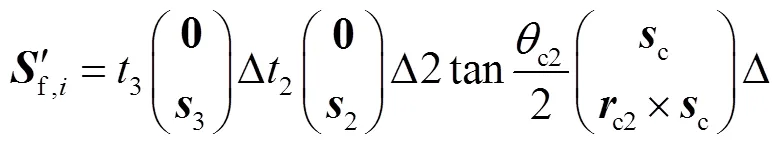
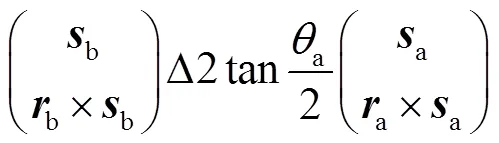
获得衍生支链P3P2RcRcRbRa、P3P2RcRbRaRa和P3P2RcRbRbRa．然后，变换上述衍生支链中移动副位置共获得21种可行支链．

类型Ⅲ：支链中具有1个移动副．

同理，将并联机构的标准支链P1P2P3RcRbRa中两个移动副P1P2替换为2个轴线互不平行的转动副RbRc，即根据式(4)做等价变换得

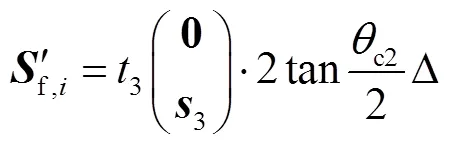
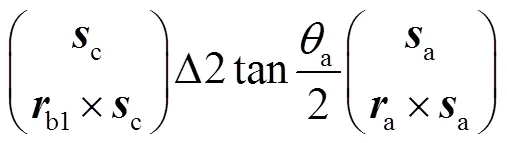
获得衍生支链P3RcRcRbRbRa、P3RcRbRbRaRa和P3RcRcRbRaRa．同理，共获得15种衍生支链．

类型Ⅳ：支链中具有0个移动副．

将标准支链中3个移动副P3P2P1替换为3个轴线互不平行的转动副RRbRa，同理可得

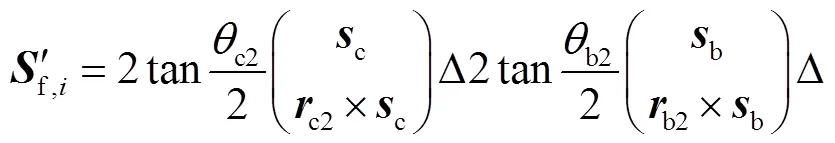
获得衍生支链RcRbRaRcRbRa．因此，在标准支链和运动副类型替换获得的衍生支链的基础上，通过改变支链中运动副的位置，共衍生出52种可行的支链构型．

1.3 装配条件与驱动关节配置

利用上述综合出的支链装配三支链六自由度并联机构，需满足

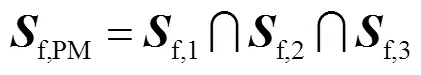
为了保证并联机构的稳定性和可控性，并联机构驱动关节的选取需满足

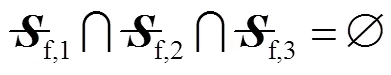
(1)每条支链应有2个驱动关节；

(2)支链中驱动关节尽量靠近机架，且最好选择移动副作为驱动关节．

同时，三支链六自由度并联机构支链中运动副的轴线之间还需满足如下约束条件：

(1) 对含有3个移动副P3P2P1RcRbRa类支链，其中(P3P2P1)3个移动副的轴线不共面也不平行和重合；

(2) 对含有2个移动副P3P2RcRcRbRa类支链，其中2个移动副P3P2的轴线不平行和重合且转动副Rc的轴线不垂直于2个移动副轴线所在平面；

(3) 对含有1个移动副P3RcRcRbRbRa类支链，其中移动副P3的轴线不垂直于转动副RcRb的轴线且两个转动副的轴线不重合；

(4) 对不含有移动副RcRbRaRcRbRa类支链，支链中各转动副RcRbRa的轴线不同时平行．

在上述分析中，从结构紧凑以及支链布置便捷程度选取5种三支链六自由度并联机构构型进行运动学分析，其分别是3-SR、3-RS、3-SR、3-RS与3-UU，如图2所示．其中，符号P、R、U、S分别代表移动副、转动副、虎克铰、球铰链，和代表主动驱动关节．

图2 三支链六自由度并联机构拓扑模型

2 运动学分析建模

上述优选出的3-SR、3-RS、3-SR、3-RS和3-UU 5种并联机构运动学分析方法相似，本节以3-SR并联机构为例对此类机构进行分析建模．

2.1 位置逆解

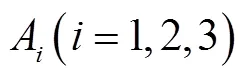
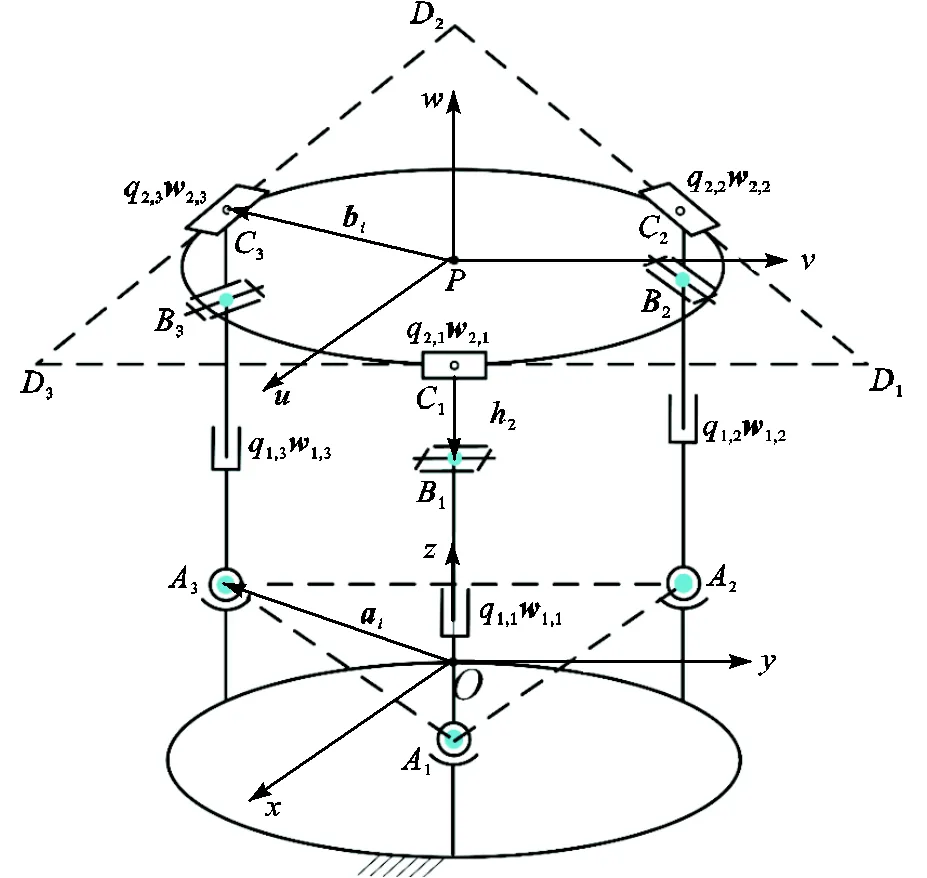
图3 3-SPRP并联机构简图

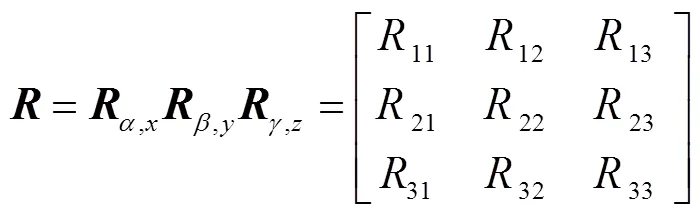
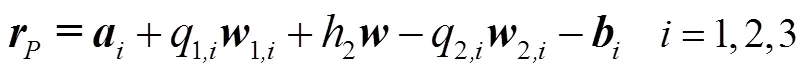
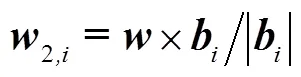
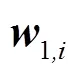
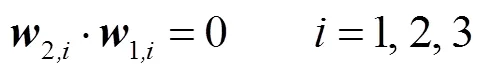
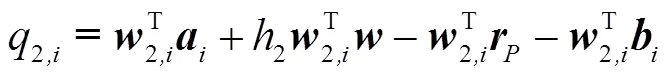
2.2 工作空间

影响并联机构工作空间的主要因素有各支链驱动杆长的最大(最小)伸长量的限制、动平台导轨上行程的限制和各球铰链转角的限制，构造如下约束条件：

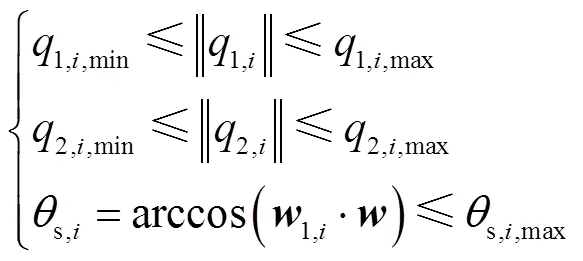
本文采用网格搜索法[22]，定义动平台末端参考点可能达到的目标搜索空间为

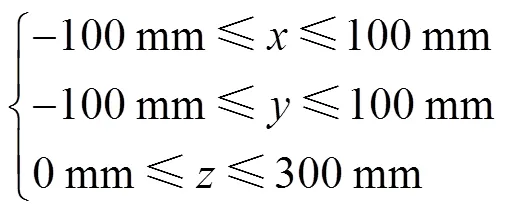
将目标搜索空间沿着静坐标系的x轴、y轴和z轴方向进行离散化，得到有限个网格节点．计算所有网格点对应位置下的逆解，满足约束条件式(19)即为位置工作空间内的有效点，并记录该点的x、y、z值．图4为动平台末端姿态()时，搜索出5种三支链六自由度并联机构位置工作空间．

2.3 速度模型

不失一般性，将SR支链中球铰链等效为3个相互垂直的转动副，所得机构有限运动模型为

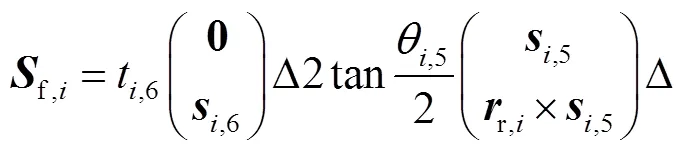
利用有限旋量与瞬时旋量之间的微分映射[23]，得到3-SR并联机构的瞬时速度模型为

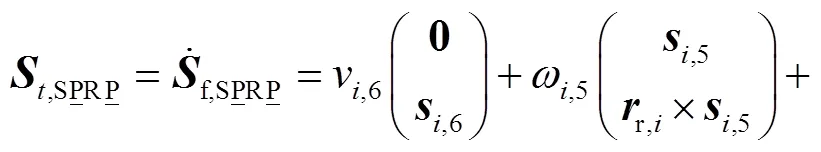
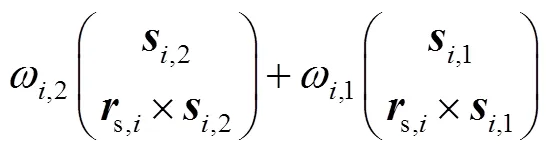
式(22)可整理为

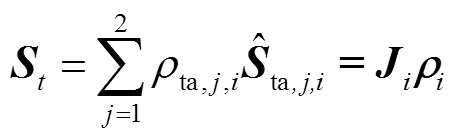
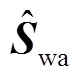
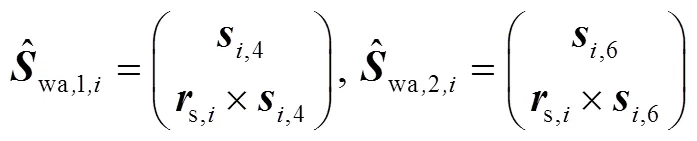
构造3-SR并联机构的力雅克比矩阵为

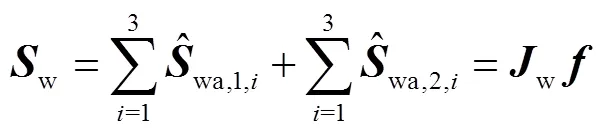
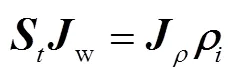
整理得

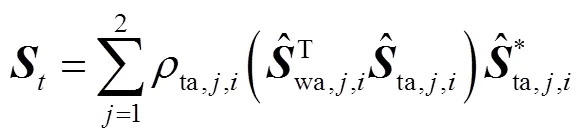
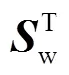
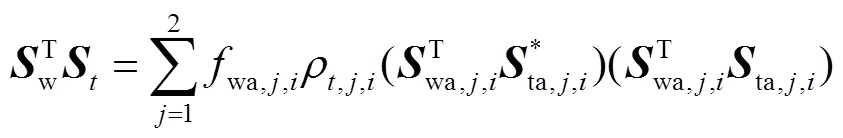
3 拓扑与性能一体化设计

3.1 运动学性能评价指标

通过运动学性能评价指标对3-SR、3-RS、3-SR、3-RS与3-UU 5个并联机构构型进行运动/力传递性能优选．因此，定义局部运动学性能评价指标

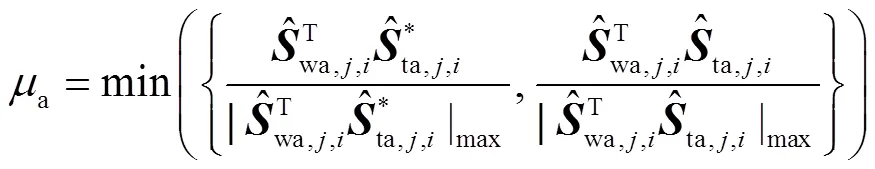
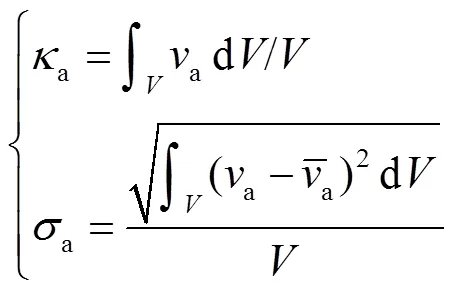
3.2 拓扑结构与运动学性能设计

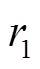
基于Isight软件的粒子群算法，通过大量的粒子(由设计变量组成)反复迭代，快速找到全局最优粒子，即优化模型为

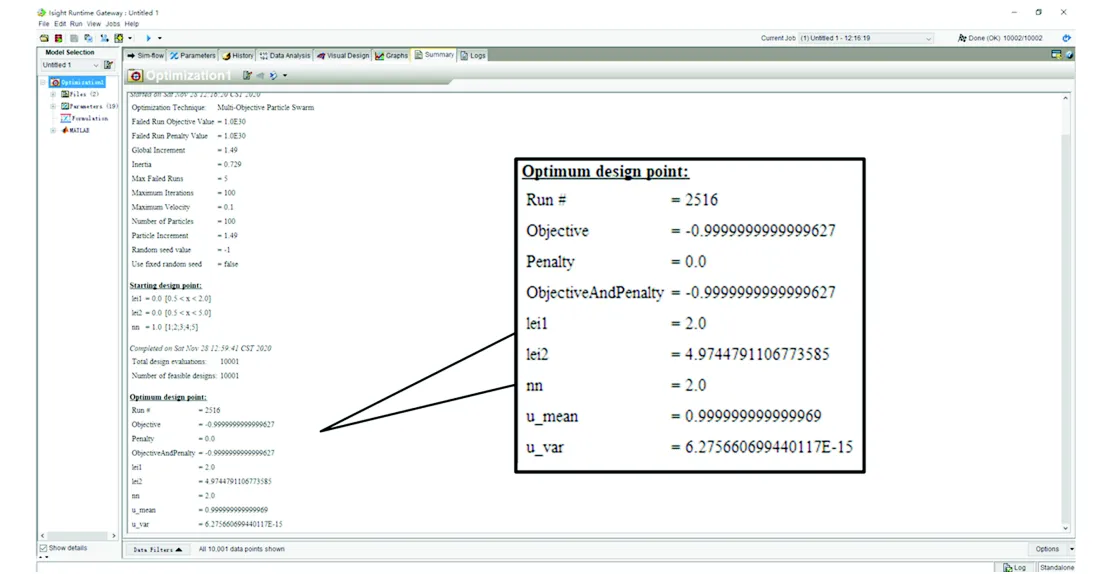
图6 利用Isight多目标粒子群的优化结果

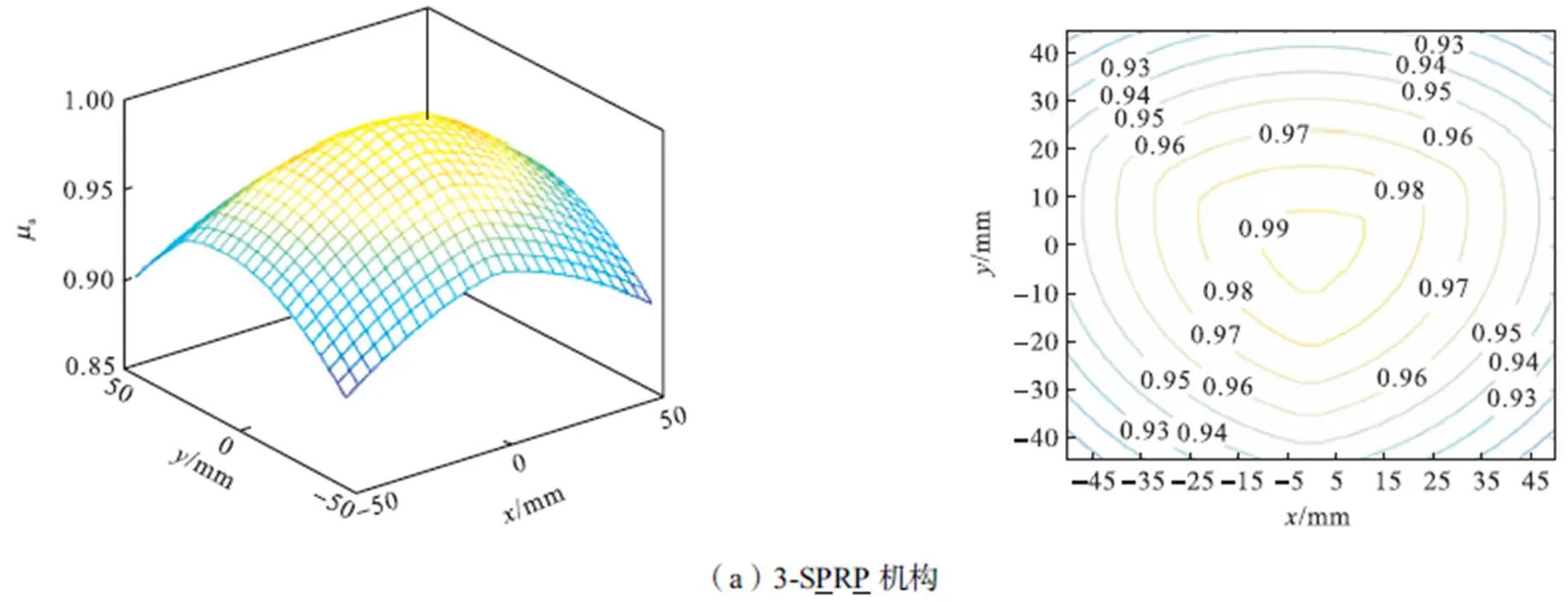
在第3.1节中，通过对比分析5种三支链六自由度并联机构的运动/力传递性能，3-SR并联机构的运动/力传递性能较优．同时，上述优化结果进一步表明3-SR并联机构具有最佳的运动/力传递性能. 综上所述，从两方面分别证明了3-SR并联机构为最佳的拓扑构型．

4 结 论

本文综合出一类三支链六自由度并联机构，进行其拓扑结构和运动学性能设计，得到如下结论.

(1) 针对现有外固定支架中支链多、造成支架质量大且在CT扫描时遮挡/干扰骨折断端造成伪影等不足，本文提出三支链六自由度并联机构外固定支架的解决方案．

(2) 以有限旋量作为数学工具，综合得到一类三支链六自由度并联机构．通过支链的装配条件和驱动关配置节条件，优选出5种三支链六自由度并联机构．并进行了5种并联机构的位置逆解、工作空间和速度建模分析，完成机构优化的准备工作．

(3) 考虑拓扑结构对运动学性能的影响因素，以工作空间内运动/力传递率的均值和方差作为性能评价指标，优选出3-SR并联机构．为后续并联外固定支架样机的制造奠定了理论基础．

［1］ Van S T，Dennison E M，Leufkens H G，et al. Epidemiology of fractures in england and wales[J]. Bone，2001，29(6)：517-522.

［2］ 赵 磊. 三种内固定方法治疗胫骨骨折的临床疗效评估[D]. 山西：山西医科大学，2013.

Zhao Lei. Three Methods of Internal Fixation Treatment of Tibia Fracture Analysis of the Clinical Curative Effect. [D]. Shanxi：Shanxi Medical University，2013(in Chi-nese).

［3］ Banerjee S，Cherian J J，Elmallah R K，et al. Robotic-assisted knee arthroplasty[J]. Expert Review of Medical Devices，2015，12(6)：727-735.

［4］ Hani E M，Ahmed E H，Yasser K. The management of tibial pilon fractures with the Ilizarov fixator：The role of ankle arthroscopy[J]. The Foot，2015，25(4)：238-243.

［5］ Vishnu C P，Mark C R，Robin M G. Staged treatment of a chronic patellar sleeve fracture using the Taylor spatial frame[J]. The Knee，2015，22(6)：672-676.

［6］ Franco L，Lodovico R B，Andrea P，et al. Treatment of non-union of the humerus using the ortho-fix external fixator[J]. Injured，2006，32(4)：35-40.

［7］ Munetomo T，Victor A V，Hiroyuki T. Foot deformity correction with hexapod external fixator：The Ortho-SUV frame[J]. The Journal of Foot & Ankle Surgery，2013，52(3)：324-330.

［8］ 黄 真，赵永生，赵铁石，等. 高等空间机构学[M]. 北京：高等教育出版社，2006.

Huang Zhen，Zhao Yongsheng，Zhao Tieshi，et al. Advanced Spatial Mechanism[M]. Beijing：Higher Education Press，2006(in Chinese).

［9］ Xie F G，Liu X J，You Z，et al. Type synthesis of 2T1R-type parallel kinematic mechanisms and the application in manufacturing[J]. Robotics and Computer-Integrated Manufacturing，2014，30(1)：1-10.

［10］ Li Z B，Lou Y J，Li Z X. Type synthesis and kinematic analysis of a new class Schönflies motion parallel manipulator[C]// 2011 IEEE International Conference on Information and Automation. Shenzhen，China，2011：267-272.

［11］Meng J，Liu G F，Li Z X. A geometric theory for analysis and synthesis of sub-6 DOF parallel manipulators[J]. IEEE Transactions on Robotics，2007，23(4)：625-649.

［12］ Li Q C，Hervé J M. 1T2R parallel mechanisms without parasitic motion[J]. IEEE Transactions on Robotics，2011，26(3)：401-410.

［13］ Li Q C，Hervé J M. Type synthesis of 3-DOF RPR-equivalent parallel mechanisms[J]. IEEE Transactions on Robotics，2014，30(6)：1333-1343.

［14］ Sun Tao，Yang Shuofei，Huang Tian，et al. A way of relating instantaneous and finite screws based on the screw triangle product[J]. Mechanism and Machine Theory，2017，108：75-82.

［15］ Sun Tao，Yang Shuofei，Huang Tian，et al. A finite and instantaneous screw based approach for topology design and kinematic analysis of 5-axis parallel kinematic machines[J]. Chinese Journal of Mechanical Engineer-ing，2018，31(1)：44.

［16］ Sun Tao，Yang Shuofei，Lian Binbin. Finite and Instantaneous Screw Theory in Robotic Mechanism[M]. Springer Nature，2020.

［17］ Sun Tao，Song Yiming，Dong Gang，et al. Optimal design of a parallel mechanism with three rotational degrees of freedom[J]. Robotics and Computer-Integrated Manufacturing，2012，28(4)：500-508.

［18］宋轶民，周 培，齐 杨，等. 一类大转角两转动并联机构的构型分析与运动学优化设计[J]. 天津大学学报(自然科学与工程技术版)，2019，52(9)：908-916.

Song Yimin，Zhou Pei，Qi Yang，et al. Topology analysis and kinematic optimization of a 2-DoF rotational parallel mechanism with large workspace[J]. Journal of Tianjin University(Science and Technology)，2019，52(9)：908-916(in Chinese).

［19］汤腾飞，方汉良，张 俊. 类Exechon并联机构模块可重构概念设计与运动学分析[J]. 天津大学学报(自然科学与工程技术版)，2019，52(7)：733-744.

Tang Tengfei，Fang Hanliang，Zhang Jun. Conceptual reconfigurable design and kinematic analysis of the Exechon-like parallel kinematic machine[J]. Journal of Tianjin University(Science and Technology)，2019，52(7)：733-744(in Chinese).

［20］ Wang Jinsong，Liu Xinjun，Wu Chao. Optimal design of a new spatial 3-DOF Parallel robot with respect to a frame-free index[J]. Science China Technological Sciences，2009，52(4)：986-999.

［21］刘辛军，谢福贵，汪劲松. 并联机器人机构学基础[M]. 北京：北京高等教育出版社，2018.

Liu Xinjun，Xie Fugui，Wang Jinsong. Fundamental of Parallel Robotic Mechanisms[M]. Beijing：Higher Education Press，2018(in Chinese).

［22］刘琳珊. 3-PRS并联机构设计方法研究[D]. 天津：天津大学，2007.

Liu Linshan. Research on Design Method of 3-PRS Parallel Mechanism[D]. Tianjin：Tianjin University，2007(in Chinese).

［23］杨朔飞. 基于有限旋量的并联机构构型综合方法研究[D]. 天津：天津大学，2017.

Yang Shuofei. Type Synthesis of Parallel Mechanisms Based upon Finite Screw Theory[D]. Tianjin：Tianjin University，2017(in Chinese).

Developing Three-Legged Six-Degree-of-Freedom Parallel Mechanism for Bone Reduction Surgery

Wang Rui，Huo Xinming，Lian Binbin，Song Yimin，Sun Tao

(Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300350，China)

With the development of minimally invasive and biological fixation technologies，precise intraoperative positioning is increasingly required in trauma and fracture surgery to ensure that the internal fixation object can accurately and minimally perform invasive fracture fixation.The use of a six-degree-of-freedom parallel external fixation robot for fracture reduction and fixation is an effective method to achieve a minimally invasive and precise reduction surgery，and it is also the future development trend of fracture surgery. The existing six-degree-of-freedom parallel mechanism comprising six branches has problems such as heavy weight and creating serious artifacts in medical imaging scans. Proposing and developing a six-degree-of-freedom parallel mechanism with fewer branches has become a research hotspot. This paper develops a three-legged six-degree-of-freedom parallel mechanism using configuration synthesis，the finite screw theory，and designs based on its topology and kinematics performance. First，the finite screw theory is used to describe the motion of the six-degree-of-freedom parallel mechanism and the end of its branch. The standard and derivative versions of the feasible branch are obtained through the synthesis and exchange law of the finite screw theory. The assembly conditions of the branch are defined，and the drive joints are configured to obtain five types of three-legged six-degree-of-freedom parallel mechanisms. Then，the instantaneous screw theory was used to analyze the inverse kinematics，workspace，and speed analysis of these five types of parallel mechanisms. Finally，the integrated design of topology and kinematic performance of the three-legged six-degree-of-freedom parallel mechanism were determined，by taking the mean and variance of the motion/force transmission rate in a given workspace as the objective function and considering the influence factors of the topology on the kinematic performance. This work provides a theoretical basis for the physical prototype construction and experimental research of the three-legged six-degree-of-freedom parallel mechanism.

three-legged six-DOF parallel mechanism；finite screw；instantaneous screw；configuration synthesis；kinematic design

TK448.21

A

0493-2137(2022)03-0273-10

10.11784/tdxbz202012062

2020-12-28；

2021-01-31.

王 蕊（1995—  ），女，博士研究生，wangrui1995@tju.edu.cn.

孙 涛，stao@tju.edu.cn.

国家重点研发计划资助项目(2018YFB1307800)；国家自然科学基金资助项目(51775367)；天津市临床医学研究中心资助项目(18PTLCSY00080)；天津市重点研发计划京津冀三地协同创新研发项目(18YFSDZC00010)；天津市科技计划资助项目(18YFZCSF00590).

Supported by the National Key Research and Development Program of China(No. 2018YFB1307800)，the National Natural Science Founda-tion of China(No. 51775367)，Tianjin Clinical Medical Research Center Project(No. 18PTLCSY00080)，Tianjin Key Research and Development Program of Coordinated Innovation Project in the Beijing-Tianjin-Hebei Region(No. 18YFSDZC 00010)，Tianjin Science and Technology Program(No. 18YFZCSF00590).

(责任编辑：金顺爱)