基于近邻子空间划分的高光谱影像波段选择方法
唐 厂,王 俊
基于近邻子空间划分的高光谱影像波段选择方法
唐 厂,王 俊
(中国地质大学(武汉)计算机学院,武汉 430074)
在降低高光谱遥感影像数据的冗余度方面,波段选择一直是一种有效的方法.近年来,提出了许多用于高光谱波段选择的聚类算法,但大多数算法只有在选择足够多的聚类中心时才能够表现出良好的性能.在选择少量波段时,往往效果很不理想,不能满足实际使用的目的.而且,随着聚类中心数量的增加,大多数波段选择算法的精度存在不同程度的下降趋势.针对当前基于聚类的波段选择方法存在对聚类中心数的强敏感性和选择的特征波段子集高相关性的问题,提出了一种基于近邻子空间划分的波段选择方法(SEASP).该方法主要包括近邻子空间划分和特征波段选取两个步骤.考虑到高光谱波段之间的有序性,SEASP首先计算出相邻波段之间的相关系数,得到相关系数向量.若两个波段之间的相关性在某个区间内最小,即相关系数的变化率在该区间内最大,说明这两个波段在很大概率上不属于同一组,为两个相邻分组之间的分割点.因此,在相关系数向量的基础上,计算出其对应的若干个极小值,通过极小值的选取来确定最终划分的子空间.最后以信息熵为度量标准从划分的子空间中选出特征波段子集.在3个公开数据集的实验结果表明,提出的SEASP算法与其他算法相比,不仅原理简单,而且在精度和计算效率方面,均表现出了更好的效果.
高光谱波段选择;相关系数;近邻子空间划分;聚类
相比于传统的RGB图像,高光谱影像具有信息量丰富、波段数目多、分辨率高等特点,因此它被广泛应用于目标检测[1]、环境监测[2]、矿物勘探[3]、农业资源调查[4]和海洋研究[5]等方面.由于其包含大量的波段信息,且相邻波段之间的特征相似度较高,这在一定程度上增加了高光谱影像分类的计算复杂度,并且还会影响分类器最终的分类精度.所以需要对高光谱影像进行降维处理,从而解决维度灾难问题.
特征提取[6]和特征选择[7]一直是数据降维领域的研究热点,这两种方法也通常作为高光谱影像降维的有效方式.在高光谱影像中,特征选择也可以称为波段选择.在无监督的波段选择方法中,基于聚类的方法都取得了较好的结果,然而文献[8]在聚类的过程中,只在单个波段或者成对波段的基础上进行判断选取,忽略了所选波段子集内部之间的关系.进一步来说,就是只考虑到划分时波段之间的相关性,忽略了最后选取的波段之间的关联.一般地,应将最后选取的波段视为一个整体而非每个单独存在的个体.在选取的波段子集中,既要保证特征波段之间差异性最大,也要保证信息量最多.文献[9]主要是采用K-MEANS算法不断计算所有样本点与当前候选中心的距离来确定最终的聚类中心,然后通过遍历所有的簇来选取特征波段.然而由于K-MEANS聚类对初始聚类中心的选取非常敏感,通常需要采用不同的初始化方法来最终确定一个较好的解决办法.另外只有当数据集样本数量较少时,该方法才能够表现出良好的性能.对于样本数量较多的数据集,其多次迭代往往需要花费大量的时间,效率较低.为了解决K-MEANS聚类算法对初始条件敏感性的问题,文献[10]提出了一种基于样本的AP聚类算法.它考量各个波段之间的相关性,然后通过最大化目标函数来获得特征波段子集.尽管它的聚类结果表现得比较稳定,然而对于包含波段数目较多的数据集,其往往具有较高的时间复杂度.
目前来看,大多数基于聚类的波段选择算法都存在对聚类中心数的强敏感性问题.具体表现在,当选取的聚类中心数较少时,精度较低;当选取的聚类中心数超过一定数量时,精度反而会随着聚类中心数的增加呈现出一种下降的趋势.这两种情况显然不满足实际需要.基于波段之间是有序排列,并且距离较远的波段之间相关性较低的思想,笔者认为按照有序波段进行划分不仅可以降低波段子空间之间的相关性,同时也能避免最后选取的特征波段之间相关性较高的问题.因此,提出了基于近邻子空间划分的波段选择算法(SEASP).SEASP采用了聚类和排序相结合的方式来解决当聚类中心数较少时精度较低的问题.本文主要工作如下:①首先计算相邻波段之间的相关系数,根据相关系数的曲率变化情况找到分组临界点,然后以临界点数目作为最终确定的聚类簇个数;②以信息熵作为波段选取的评价指标,在对每个聚类簇进行波段选取时,将信息熵作为权重对每个波段排序,然后选择信息熵最大的波段作为特征波段,这样可以确保最终选取的波段包含相对完整的信息.
1 本文算法
1.1 近邻子空间划分
基于相邻波段之间的相关性比非相邻波段之间的相关性高这一特点,笔者认为在一定范围之内的连续波段有着极大的概率被划分为同一簇.因此与传统的基于聚类的波段选择算法不同的是,在SEASP中,只计算相邻波段之间的相关性,这在一定程度上减小了计算量,从而更加快速地实现高光谱影像子空间的划分.
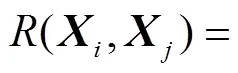
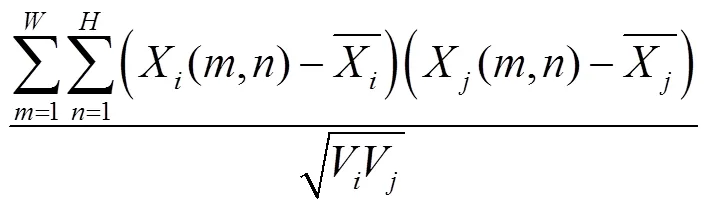
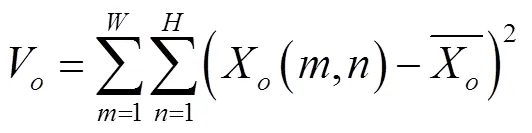

在聚类算法的思想中,衡量划分的标准通常是使得类内相关度最高,类间相关度最低.基于此,在SEASP中,主要是根据相关系数的变化率来确定分组之间的相关性大小.具体来说,若两个波段之间的相关性在某个区间内最小,即相关系数的变化率在该区间内最大,说明这两个波段在很大概率上不属于同一组,为两个相邻分组之间的分割点.考虑到波段之间的有序性和非近邻空间的弱相关性,笔者只计算相邻波段的相关系数,因此聚类划分问题便转化为在有序数据集中寻找分组之间的间断点问题.根据相关系数寻找极值点的计算公式为
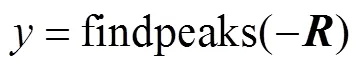
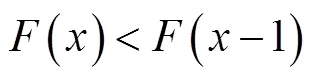
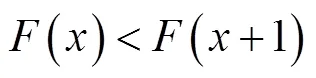
通过极小值点的选取来确定有序波段之间的间断点,从而得到划分的波段子空间.具体流程示例如图1所示.
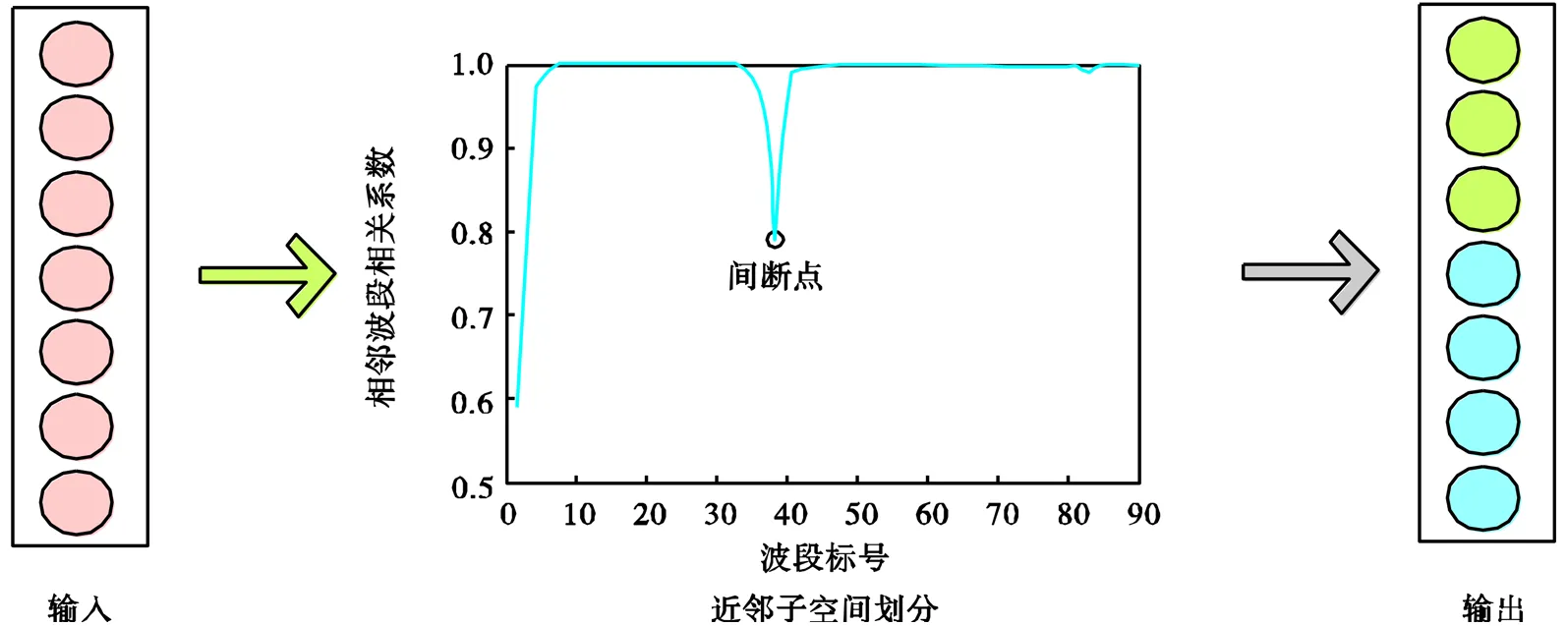
图1 近邻子空间划分示例
1.2 特征波段选取
信息熵用来衡量图像中包含的平均信息量的大小,一个图像的信息熵越大,那么该图像所包含的信息也就越丰富.基于此观点,笔者将信息熵作为衡量波段重要性程度的一个度量指标.在一个波段子空间中,将其包含的所有波段按照信息熵的大小进行排序,然后从中选取信息熵最大的波段作为特征波段.信息熵的计算公式为

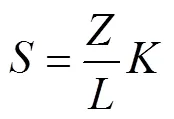

图2 Indian Pines信息熵
关于SEASP算法的更多细节,笔者在SEASP算法流程和图3中进行了总结.
算法1:SEASP.
输出:特征波段子集.
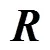
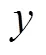

步骤4 根据式(7)计算每个波段的信息熵.

图3 SEASP算法示例
2 波段选择实验与结果分析
在本节中,笔者进行了大量的实验来验证所提出的SEASP算法在高光谱波段选择上的有效性.首先,介绍常用的3种高光谱影像数据集,然后简要概括所比较算法的原理和流程.接着便是对此次实验的设置条件进行了描述,其中包括分类器及其参数的选取、波段数目范围的选取以及精度度量标准的选取.最后对这几种方法在实验数据集和分类器上表现出的性能进行详细的分析,从而验证SEASP方法的有效性和可行性.SEASP的实现代码已上传至https://github.com/WangJun2023/SEASP.
2.1 数据集介绍



2.2 比较算法介绍
为了验证所提出算法的有效性,笔者选取了几种比较先进的算法作为竞争对手.下面将对这几种算法做一个简要的介绍.
ASPS_MN、ASPS_IE[11]:该算法首先将高光谱影像立方体根据设置的选择波段数目进行等宽划分,然后采用最大化类间距离和类内距离之比进一步确定分组之间的分割点,最后分别从每个分组中按照最小噪音值和最大信息熵的量度标准选取目标波段子集.针对ASPS_MN算法,在实验中笔者采用原论文的参数设置,随机选取块的比例为10%,并设置每块的大小为10×10像素.
TOF[12]:该算法主要是采用动态规划的思想将高光谱影像立方体划分为若干个子立方体,然后利用E-FDPC[13]方法计算出来的分数从该若干个子立方体中选择特征波段子集.
UBS[14]:该算法根据设置的选择波段数目将高光谱影像立方体分割为等宽的子立方体,然后将分割点作为最后选择的特征波段.
FNGBS[15]:该算法主要是采用基于邻域波段分组思想对高光谱影像立方体划分,然后从中选取局部密度与信息熵乘积最大的波段作为特征波段.
2.3 实验条件设置

波段数目范围选取:对于3个公共的高光谱影像数据集,由于目前其最佳选择的波段数目未知,所以在本次实验中,选取波段数目的范围为5~50.为了充分展示波段数目设置的随机性,实验选取的波段数目一共有12个,分别为5、7、10、15、26、30、36、39、42、44、47、49.
精度标准选取:本次实验采用了3种度量标准来对分类的结果进行分析,分别为总体精度(OA),平均总体精度(AOA)以及Kappa系数(Kappa).
2.4 结果展示
为了验证所提出的算法的有效性,笔者将分别对这几种算法在3个数据集上表现出的性能进行一个详细分析,最后再从运行时间的角度上验证其可行性.此外在算法的性能比较方面,还考虑了所有波段作为特征波段.在本次实验中,所有比较方法均在Matlab 2016a上运行,CPU为i7-5500U,2.40GHz,内存8Gb.
表1展示了竞争算法在3个公共数据集上所表现出的AOA和Kappa.其中,在进行测试比较时,3个数据集选取的波段数目分别为36、5和5,AOA为10次运行结果的范围.下面则是对这几种算法在3个数据集上的性能表现进行一个详细的分析.
表1 AOA和Kappa结果展示

Tab.1 Results of AOA and Kappa %
Botswana数据集:从图4可以看出,笔者所提出的算法在一些特定的波段数目上所表现出来的性能优于其他算法.特别是当选择的波段数目大于25时,SEASP与其他算法相比具有明显的优势,并且始终保持一个稳定性,而其他算法则处于上下波动状态.此外,从所有分类器的结果可以看出,当选择的波段数目较少时,ASPS_MN的结果不如其他算法,这也反映出其对选择波段数目的强敏感性.
只有当选择的波段数目达到一定数量时,其才能够表现出一个更好的性能.从整体来看,随着选择波段数目的不断增加,SEASP所表现出的结果变化幅度并没有其他算法那么大,这也侧面验证了其对选择波段数目的敏感性是较小的,同时说明了其在少量选择的波段数目上也能够表现出不错的性能.

图4 Botswana数据集精度
Salinas数据集:从表1和图5可以看出所提出的算法与其他算法相比也能够表现出不错的结果,其中在某些点上,是完全优于其他所有算法.从3个分类器的表现结果看,虽然提出的算法优势不是很明显,但是随着选择波段数目的增加,SEASP基本上是处于稳定上升的状态,没有出现明显的反弹现象.而其他算法则不太稳定,当选择的波段数目变多时,相反结果还会出现下降的趋势.在图5(c)中,当选择波段数目小于35时,SEASP明显优于其他所有算法.值得注意的是,在图5(a)和图5(b)中,当选择波段数目从5增加到49时,所提出的算法结果变化幅度仅为2%和3%左右,而其他算法的变动均超过了3%,有的算法甚至超过了5%.这再次验证了SEASP对选择波段数目的弱敏感性,即对于选择波段数目较少的情况,也能够表现出优越的性能.
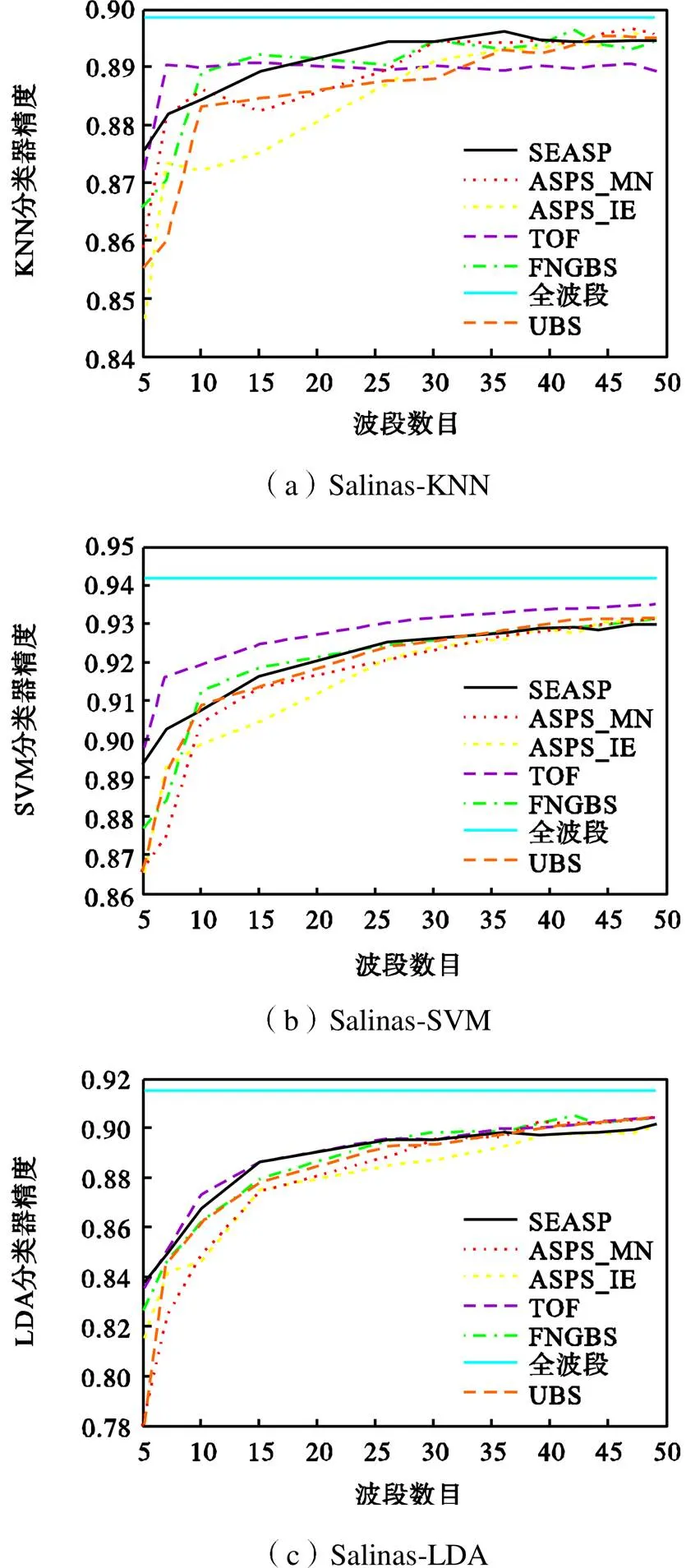
图5 Salinas数据集精度
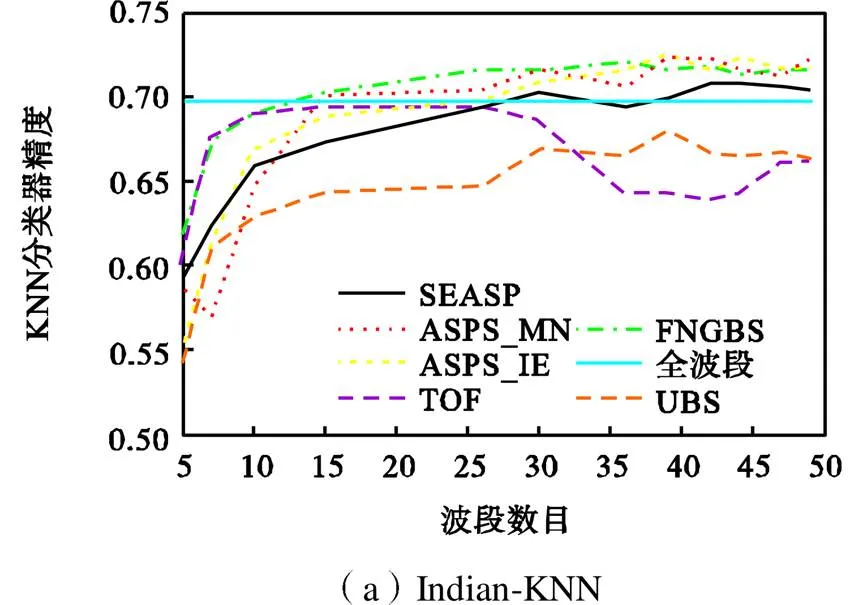
Indian Pines数据集:从表1和图6中可以看出,所提出的算法与其他算法相比也具有可比性.特别是当选取的波段数目为5时,在KNN分类器的表现上,SEASP与FNGBS算法具有一定的可比性,但明显地高于其他所有算法.从算法的鲁棒性来看,在3个分类器上,SEASP均表现出了稳定上升的趋势,而其他算法都存在下降的现象,并且有的算法波动幅度较大,比如图6(a)中的UBS和TOF.这反映了随着选取波段数目的增加,这些算法都不可避免地选取了一些冗余波段,这就导致了分类精度的下降.而笔者所提出的算法则不会出现这个明显的现象,也说明了在选取波段时,SEASP充分考虑到最后选择的目标波段之间强相关性的问题,从而改正了大多数基于聚类的波段选择算法的不足.
为了进一步验证所提出方法的可行性,笔者在3个数据集的波段选择上还计算了所有竞争算法的时间.其中,在3个数据集的波段选取数目上面,笔者分别设置为10、15、20,呈现出一种递增的趋势.表2给出了不同算法在不同数据集上选择同样数目波段所耗费的时间.从表2结果中可以看出,UBS算法的计算成本与其他算法相比少得多,这主要是因为其仅仅是一个简单的划分操作.它将整个数据集划分为等宽的子立方体,然后选取划分点作为特征波段.除UBS算法外,与其他算法相比,笔者提出的算法所花费的计算时间处于一个适中的范围.除在Botswana数据集上表现的计算时间不是很理想之外,其他数据集上的计算时间均表现良好.其中,Botswana数据集所花费时间较长的原因是其包含的波段之间相关性变化趋势过于频繁,这导致了SEASP在确定波段子空间之间的分割点时所需要的计算成本较大,间接性地提高了运行时间.但是通过这个计算过程,其显著地提高了在这个数据集上的分类精度,具体结果如表1和图4所示.同时与其他算法所耗费的时间来 看,差距不是很大,故笔者认为这个耗费成本是可以接受的.
综上可知,所提出的算法不仅原理简单,而且在3个公共数据集的分类性能上与其他算法具有一定的可比性,甚至优于其他算法,另外其执行速度也是较快的,从而验证了该算法的有效性和可行性.
表2 不同波段选择算法的计算时间对比

Tab.2 Contrast in the computational time of the different methods on three hyperspectral datasets s
3 结 语
考虑到目前大多数基于聚类的波段选择算法存在对聚类中心数的强敏感性和选择的特征波段子集高相关性问题,笔者提出了SEASP.基于高光谱波段之间的有序性和非相邻波段之间的弱相关性,SEASP首先计算相邻波段之间的相关性,根据相关系数的曲率变化情况找到显著性的分组临界点,然后以临界点数目作为最终确定的聚类簇个数.最后在对每个聚类簇进行波段选取时,将信息熵作为权重,这样可以确保最终选取的波段包含相对完整的信息.在3个公开的数据集上的实验证明,所提出的算法不仅原理简单,而且与其他算法相比具有更好的鲁棒性和有效性.在未来的研究工作中,笔者将进一步研究如何更加快速准确地确定聚类簇之间的分界点,而不仅仅是依据波段之间的相关系数.
[1] Liang Jie,Zhou Jun,Tong Lei,et al. Material based salient object detection from hyperspectral images[J]. Pattern Recognition,2018,76:476-490.
[2] Gao B,Lu A,Pan Y,et al. Additional sampling layout otimization method for environmental quality grade classi-fications of farmland soil[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2017,10(12):5350-5358.
[3] Zadeh M H,Tangestani M H,Roldan F V,et al. Mineral exploration and alteration zone mapping using mixture tuned matched filtering approach on ASTER data at the central part of Dehaj-Sarduiyeh copper belt,SE Iran[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2014,7(1):284-289.
[4] Lu B,Dao P D,Liu J,et al. Recent advances of hyperspectral imaging technology and applications in agriculture[J]. Remote Sensing,2020,12(16):2659-1-2659-40.
[5] Kobryn H T,Wouters K,Beckley L E,et al. Ningaloo reef:Shallow marine habitats mapped using a hyperspec-tral sensor[J]. PloS One,2013,8(7):e70105-1-e70105-22.
[6] Jiang J,Ma J,Chen C,et al. SuperPCA:A superpix-elwise PCA approach for unsupervised feature extraction of hyperspectral imagery[J]. IEEE Transactions on Geo-science and Remote Sensing,2018,56(8):4581-4593.
[7] 顾翔元,郭继昌,田煜衡,等. 基于条件互信息的空域隐写检测特征选择算法[J]. 天津大学学报(自然科学与工程技术版),2017,50(9):961-966.
Gu Xiangyuan,Guo Jichang,Tian Yuheng,et al. Spa-tial steganographic detection feature selection algorithm based on conditional mutual information[J]. Journal of Tianjin University(Science and Technology),2017,50(9):961-966(in Chinese).
[8] Ahmad M,Haq D I U,Mushtaq Q,et al. A new statisti cal approach for band clustering and band selection using K-means clustering[J]. Int J Eng Technol,2011,3(6):606-614.
[9] Xie F,Li F,Lei C,et al. Representative band selection for hyperspectral image classification[J]. ISPRS International Journal of Geo-Information,2018,7(9):338.
[10] Qian Y,Yao F,Jia S. Band selection for hyperspectral imagery using affinity propagation[J]. IET Computer Vi-sion,2009,3(4):213-222.
[11] Wang Q,Li Q,Li X. Hyperspectral band selection via adaptive subspace partition strategy[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Re-mote Sensing,2019,12(12):4940-4950.
[12] Wang Q,Zhang F,Li X. Optimal clustering framework for hyperspectral band selection[J]. IEEE Transactions on Geoscience and Remote Sensing,2018,56(10):5910-5922.
[13] Jia S,Tang G,Zhu J,et al. A novel ranking-based clus tering approach for hyperspectral band selection[J]. IEEE Transactions on Geoscience and Remote Sensing,2016,54(1):88-102.
[14] Chang C I,Wang S. Constrained band selection for hy perspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing,2006,44(6):1575-1585.
[15] Wang Q,Li Q,Li X. A fast neighborhood grouping method for hyperspectral band selection[J]. IEEE Transactions on Geoscience and Remote Sensing,2021,59(6):5028-5039.
A Hyperspectral Band Selection Method via Adjacent Subspace Partition
Tang Chang,Wang Jun
(School of Computer Science,China University of Geosciences,Wuhan 430074,China)
Band selection is regarded as an effective method for reducing the redundancy of hyperspectral remote sensing images. In recent years,many clustering algorithms have been proposed for the selection of hyperspectral bands,but most of them perform well only when enough clustering centers are selected. When selecting a small number of bands,the results of these algorithms are often not ideal and are unsuitable for practical usage. Furthermore,the accuracy of most band selection methods tends to decrease when the number of selected bands increases. To address the high correlation of selected feature band subsets and the sensitivity to the number of cluster centers in the current clustering-based band selection methods,this study proposes a simple yet effective hyperspectral band selection method via adjacent subspace partition(SEASP). The proposed algorithm comprises two parts:the partition of subspace and selection of feature bands. By considering the order between adjacent hyperspectral bands,the SEASP calculates the correlation of the adjacent bands to first obtain the correlation coefficient matrix. If the degree of the correlation between two bands is the smallest within an interval,i.e.,the rate of change of the correlation coefficient is the largest within that interval,these two bands should not belong to the same group in a large probability,indicating a segmentation point of two adjacent groups. Thus,the corresponding minimum values via the correlation coefficient matrix are obtained,and the final subspace is then determined through the selection of the minimum values. Finally,the subset of feature bands is selected from the subspace based on the information entropy. Extensive experiments on three public datasets show that the proposed SEASP not only has a simple form in principle but also shows better results in terms of accuracy and computational efficiency than other state-of-the-art algorithms.
hyperspectral band selection;correlation coefficient;adjacent subspace partition;clustering
TP751
A
0493-2137(2022)03-0255-08
10.11784/tdxbz202012004
2020-12-02;
2021-01-04.
唐 厂(1987— ),男,博士,教授,tangchang@cug.edu.cn.
王 俊,wang_jun@cug.edu.cn.
国家自然科学基金资助项目(61701451,62076228);南京理工大学社会安全信息感知与系统工业和信息化部重点实验室创新基金资助项目(202007).
Supported by the National Natural Science Foundation of China(No. 61701451,No. 62076228),the Key Laboratory of Information Perception and Systems for Public Security of MIIT(Nanjing University of Science and Technology)(No. 202007).
(责任编辑:王晓燕)

