基于改进烟花算法的中俄商品多式联运路径优化
万 杰,龙云飞,陈星瀚
基于改进烟花算法的中俄商品多式联运路径优化
万 杰,龙云飞,陈星瀚
(河北工业大学经济管理学院,天津 300401)
中俄双边贸易随着“一带一路”倡议的深入落实呈现出稳定增长的态势,商品需求量的增多以及需求时间的多样化使得商品运输方式发生了重大转变,运输方式由原来的单一运输转变为现在的多式联运.通过多式联运构建综合交通运输方案,既能够满足商品需求量的激增以及商品需求时间的多样化,同时又能够发挥不同运输方式之间的优势,形成优势互补.为了求解多式联运物流路径优化问题,本文以中俄贸易区间的运输路线与运输方式为研究对象,综合考虑中俄贸易区间的商品种类、需求特点以及运输方式,建立了以运输成本、运输时间、碳排放量为优化目标的多目标优化模型.针对中俄贸易实际运输情况,本文仅考虑公、铁、海3种运输方式之间的多式联运,同时针对所构建模型的随机性和隐并行性,设计了求解该模型的改进烟花算法(improved FWA).通过以中俄两国之间的多品类商品运输为例进行算例分析,获得了多式联运运输路线的Pareto非劣解以及相应的运输成本、运输时间和碳排放量,并且与基本烟花算法进行对比,验证了模型和改进算法的有效性.同时,本文以运输时间作为灵敏度分析变量,分析不同时间需求下,运输方案在运输成本、运输时间和碳排放量3个属性之间的变动趋势,为中俄多式联运物流发展提供决策参考.
综合交通运输;需求变动;多式联运;改进烟花算法
俄罗斯作为“一带一路”倡议的重要支点和合作伙伴国家,据中国海关总署统计结果显示,2018年中俄双边贸易额达1070.6亿美元,同比增长27.1%,创历史新高.其中我国对俄罗斯出口689.4亿美元,增长9.1%,自俄进口381.2亿美元,增长39.4%.在中俄运输过程中需要涉及多种运输方式,因为单一的运输方式很难再满足中俄之间庞大的物流需求,多式联运能有效对固有的运输方式实现优势互补,并缩短运输时间、降低运输成本等.当今,中俄携手达成新时代全面战略协作伙伴关系,本文研究中俄间的多式联运物流路径选择问题具有重要的现实意义.
近年来,学者们对于跨境多式联运物流路径优化问题,主要针对物流过程中不同的影响因素建立模型并应用启发式算法求解.Cho等[1]以成本和时间为目标提出了加权约束最短路径(WCSPP)模型,求解从釜山到鹿特丹的实际运输路线优化;付新平等[2]、Seo等[3]同样考虑运行时间和费用等因素建立动态分析模型计算中国城市到欧洲城市的国际集装箱多式联运线路;李玉民等[4]考虑运输时间、费用和碳排放量等因素,构建多式联运路径优化模型求得运输方案Pareto解.在应用算法求解时,Hao等[5]运用动态规划算法获得多式联运的最优组合策略;Qu等[6]考虑混合整数规划方法,应用CPLEX在AMPL编程语言中求出精确解;Adil等[7]考虑多式联运过程中的复杂决策问题,使用LINGO对混合整数规划模型求解.同时,精确算法的求解效率较低,当前学者们利用智能启发式算法求得可行解.Chang等[8]根据中国海铁联运网络的特点,构建了虚拟网络将路径选择问题转化为双目标最短路径问题,利用启发式算法进行求解;汤银英等[9]考虑不同运输方式的能力以及时间窗,使用NSGA-II以及二阶段编码的方式求得Pareto非劣解;万杰等[10]考虑成本和时间等目标建立多式联运路径优化模型,利用混合算法对实际问题进行 求解.
综上,虽然相关的研究内容较为丰富,但考虑到中俄间的商品贸易往来密切,物流的需求量会因各类影响因素的出现产生商品的需求变动,在特殊条件下的物流配送使得原本稳定的物流系统失衡,当物流时间延长时,某些应急商品或特殊商品容易产生变质或紧急供给量不足等情况.
因此,本文考虑需求变动的情况提出一种新的物流方案,两国根据商品的需求特性选择运输方案.从中俄物流运输现状出发,将多式联运与中俄贸易实际情况相结合[11-13],综合分析了国内城市至俄罗斯的运输成本,建立以运输成本、运输时间、碳排放量为优化目标的多目标模型,设计求解该模型的改进烟花算法,为中俄区间的多式联运物流路径优化问题提供参考.
1 中国至俄罗斯运输方式概述
中俄间商品的运输方式有铁路运输、海运运输、公路运输以及航空运输,每种运输业务都呈现多元化发展.但航空运输的单程货物量较少,费用高,并不适合开展长期大量的货物贸易运输,所以该运输方式不在本文的研究范围内.
1.1 中俄水路运输现状
水路运输是中俄间重要的货运方式,其基本特点是利用天然水道进行货物运输,虽然运输速度慢但容量大,且成本较低.东方港是西伯利亚大陆桥的东部起点,我国很多港口都有直达俄罗斯东方港的航线.同时,在远东海岸线上共分布着32个海港,包括22个商港、10个渔港和约300个小港口及港湾.其中符拉迪沃斯托克港至大连港的距离约为2000km.这个港口对中俄的经贸关系起着十分重要的作用.
中俄海运运输路线主要有4条:①从中国港口出发,经由海运运输到俄罗斯符拉迪沃斯托克、东方港等口岸,在口岸进行清关等操作之后通过铁路运输至目的地,目的地为俄罗斯东部城市的多选用此条路线;②经俄罗斯圣彼得堡港口,在圣彼得堡进行清关,通过货物拖车或铁路运输到各大城市,此路线适合运输到俄罗斯西部的货物;③途径黑海地区,先到达俄罗斯的新罗西斯克港口,再中转到索契等地区;④先到达德国汉堡,再中转到俄罗斯的内陆城市.中国至俄罗斯的货运港口主要有大连港、天津港、青岛港、上海港以及福州港.
1.2 中俄铁路运输现状
铁路运输具有运输能力强、安全性高及受气候影响小的特点.中俄铁路运输主要以中欧班列为载体,其中途径俄罗斯的班列有渝新欧、郑新欧等线路,分别从重庆、郑州等城市出发经由阿拉山口、满洲里和二连浩特出境,可到达俄罗斯的主要城市包括莫斯科、圣彼得堡、叶卡捷琳堡、秋明、乌法等.
1.3 中俄公路运输现状
公路运输是中俄运输中的另一条重要通道,中国与俄罗斯接壤的主要城市有满洲里、黑河、绥芬河等.常用的海关口岸是黑龙江省口岸、新疆的阿拉山口口岸和霍尔果斯口岸,主线分别是从黑龙江省口岸报关出境,到达俄罗斯口岸进行清关,再转运到乌苏里斯克转换成铁路运输至俄罗斯全境;另一条是从新疆阿拉山口或霍尔果斯等口岸,途径哈萨克斯坦最终到达俄罗斯目的地城市,中俄商品运输情况如图1 所示.
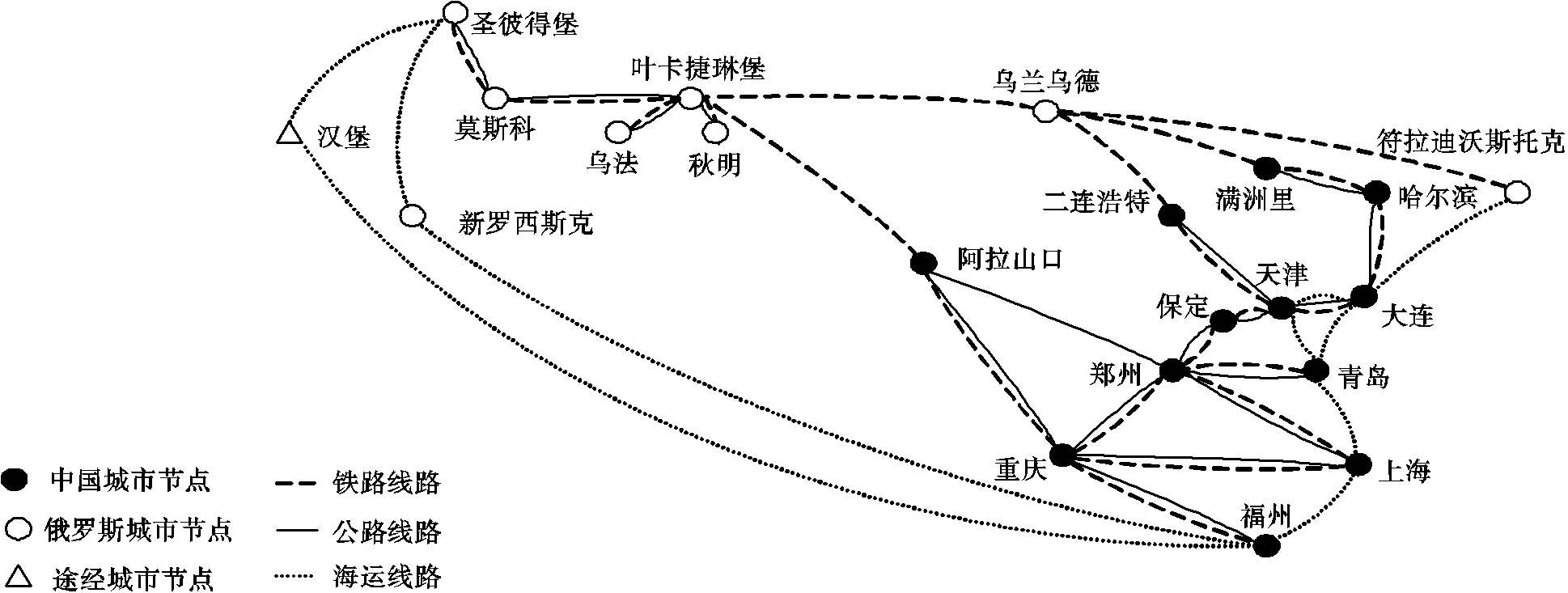
图1 中俄商品运输路线
2 问题描述与模型建立
2.1 问题描述
假设一批中国生产的商品分布在A、B两个城市,需要运输到俄罗斯某城市(E);货物可从不同的城市节点直接到达目的地,也可汇集到某一城市节点(C或D)后一同运往E,节点之间均有多种运输方式可供选择,如图2所示,虚线箭头表示商品在节点内完成不同运输方式的换装.建立模型时考虑了货物的包装成本,因运输的货物可能含有金属成分,海运时可能产生盐雾锈蚀现象,则选择海运时的包装成本与其他运输方式不同,且商品价值不同的货物的保险成本不同.模型求解商品从起点运输至终点过程中的路径及运输方式.
假设条件:
(1) 在两个城市节点之间只使用一种运输方式来运送货物;
(2) 城市节点处无容量限制;
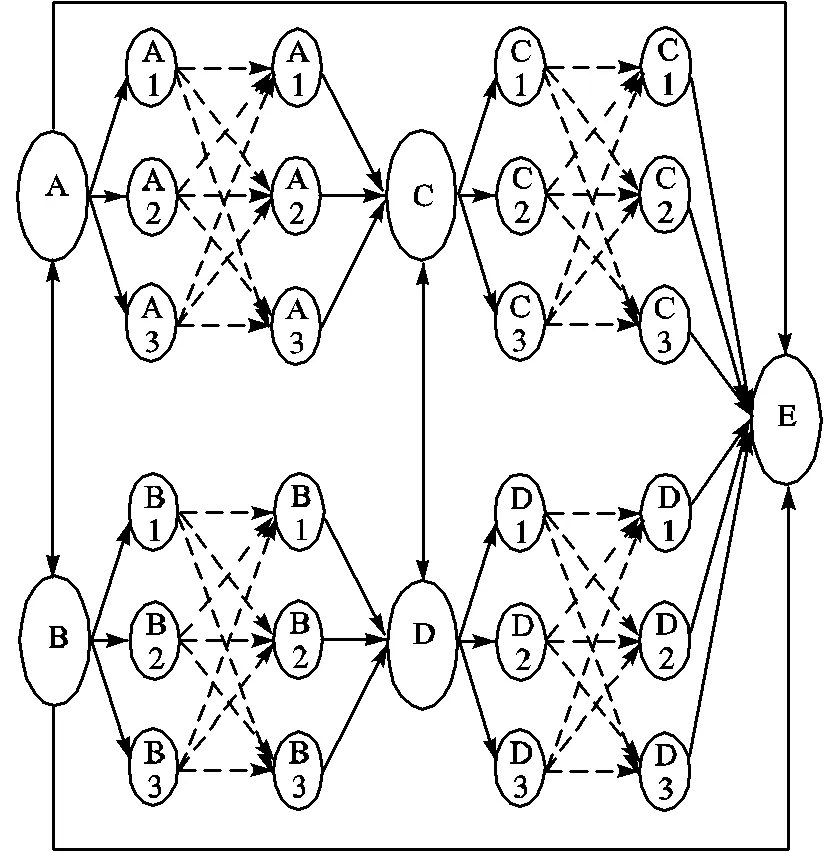
图2 多式联运物流网络
(3) 货物的转运只能在城市节点处发生;
(4) 城市节点处的设施设备均满足运输方式之间的转换要求;
(5) 到达俄罗斯城市节点的时间等于到达目的地的商品运输总时间.
2.2 模型建立
模型的参数及定义如表1所示.
表1 模型的参数及定义

Tab.1 Model parameters and definitions
多目标函数:
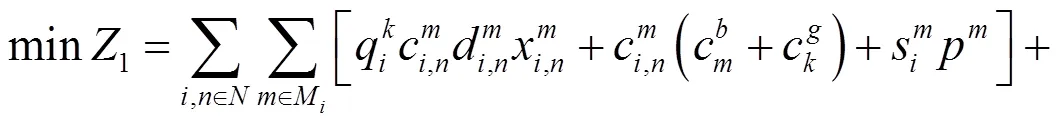
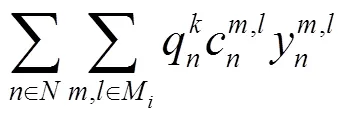
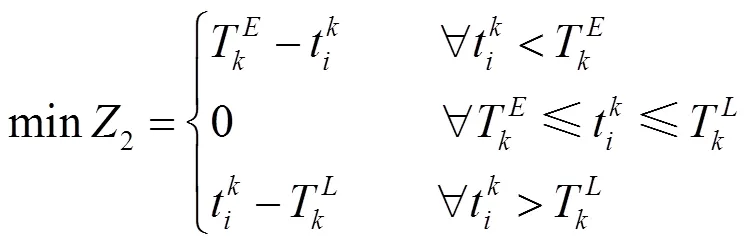

约束条件:
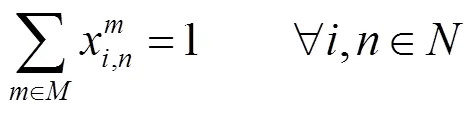
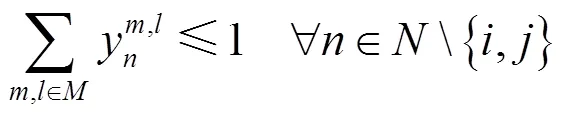
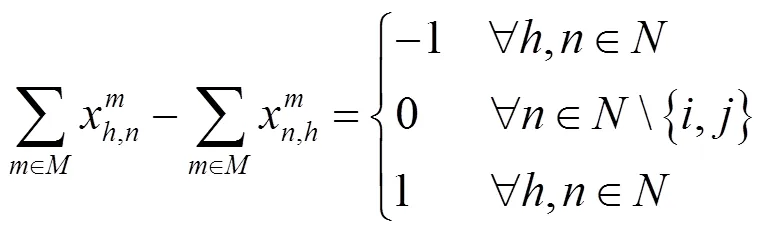

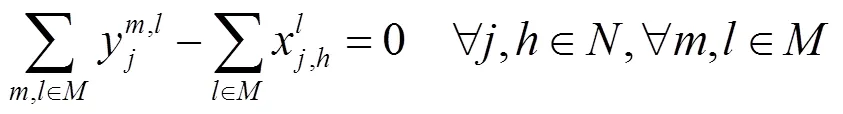
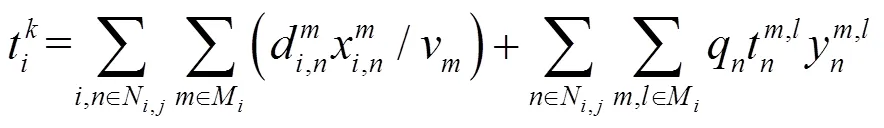
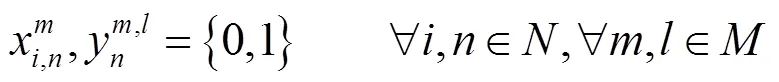
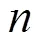
3 基于改进烟花算法的模型求解
3.1 改进烟花算法
动态搜索烟花算法(dynamic search fireworks algorithm)是由谭营等[14]首先提出,其性能优于传统的烟花算法,是对于烟花算法的一种改进.烟花算法的参数较少,执行过程简单,尤其在解决高维复杂优化问题上具有一定优势.针对随机性问题[15]和多目标问题[16],适合采用此算法进行改进.在动态搜索烟花算法中,烟花被放到潜在的搜索空间,并为每个烟花启动爆炸过程,爆炸之后,火花充满了烟花周围的空间.烟花以及新产生的火花代表了搜索邻域范围内的潜在解决方案.
改进烟花算法的工作原理如下:首先,随机选取若干个烟花,计算其适应度函数,初始化核心烟花的爆炸半径,计算非核心烟花的爆炸半径和火花数量. 其次,烟花爆炸产生不同类型的火花,进行映射操作.最后,更新核心烟花的爆炸半径,从烟花和火花中挑选出候选烟花进入下一次迭代.
3.2 算法过程

(1) 初始化.随机选取种由起点到终点的运输路径方案,计算其初始方案的适应度函数,在本文中将总成本最小作为适应度函数.将当前最优运输路径方案设置为核心烟花(CF),则除了核心烟花外,其余所有的烟花组成的集合称为非核心烟花(Non-CFs).
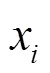
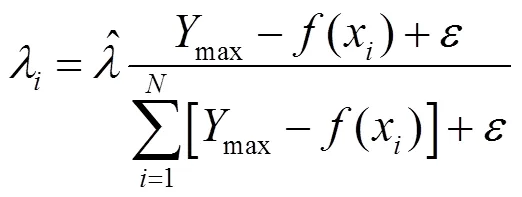
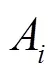
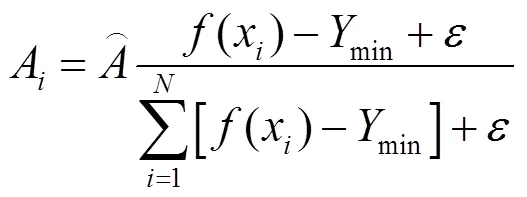
对于核心烟花来说,其爆炸幅度是根据上一代的搜索结果进行调整的,在第1代,核心烟花是所有随机初始化烟花中最好的,其振幅预设为常数,通常是搜索直径,核心烟花的爆炸半径计算式为
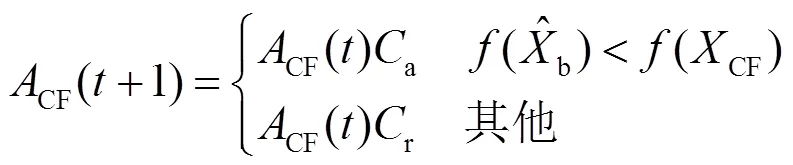
与核心烟花相比,非核心烟花会在可行域范围内更远的距离产生少量的爆炸火花,核心烟花出现局部最小值时,这一组烟花通常可以避免算法过早陷入局部最优,得不到满意解,上述步骤如图3所示.
(3) 映射操作.当某一个烟花靠近可行域的边界时,在爆炸操作中产生的火花可能会超出所给出的可行域.若出现此现象,则需要使用映射操作:
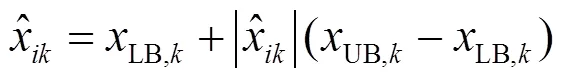
(4) 选择操作.运用爆炸操作之后,从当前的烟花和爆炸火花中选择一部分作为新一代的烟花,在动态搜索烟花算法中,适应值最优的个体首先被选为下一个迭代的烟花,而其余的烟花是从其余个体中随机选择的.改进烟花算法流程如图4所示.
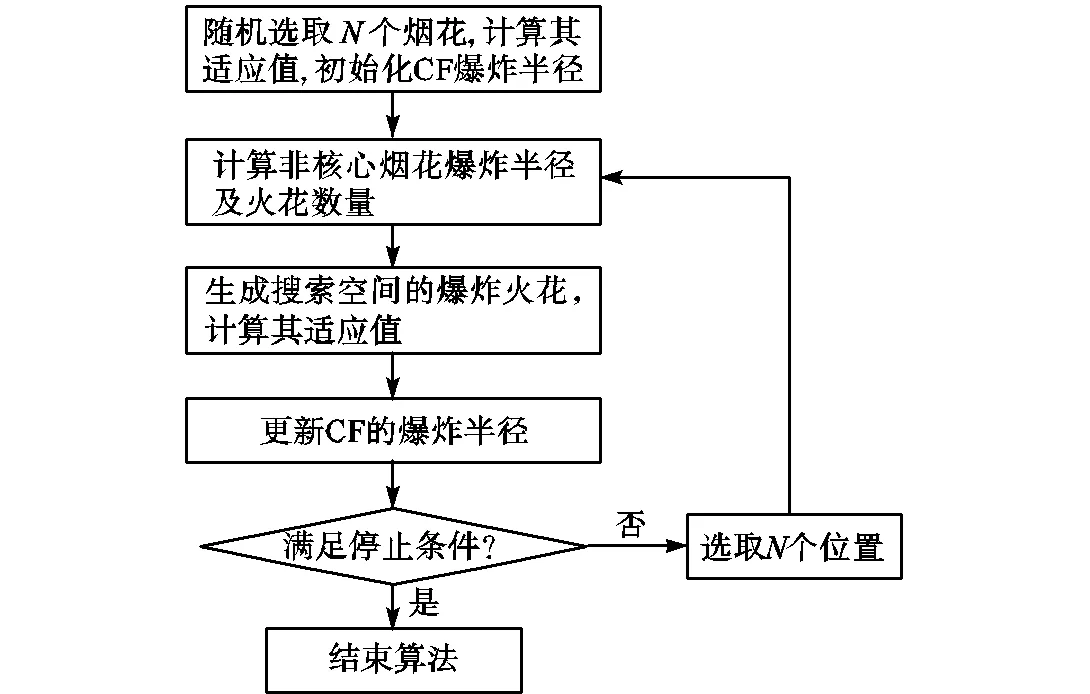
图4 改进烟花算法流程
4 实验分析
4.1 实例描述

表2 运输商品信息
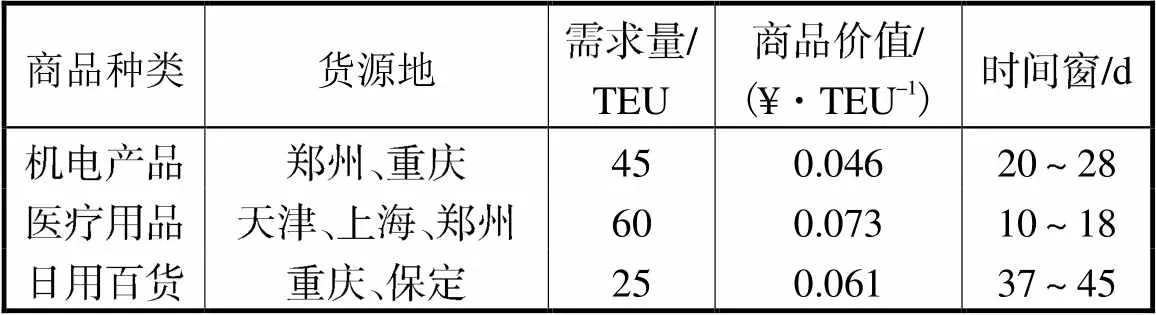
Tab.2 Shipping commodity information
城市节点之间有公路、铁路和水运3种运输方式可供选择.由于大多数机电产品内部含有金属元器件,海运时容易产生盐雾腐蚀现象,所以海运时的包装费用设置为300¥/TEU.3种运输方式的单位运价、平均运行速度、单位中转费用和中单位转时间如表3所示.城市节点之间的各运输方式交通营运里程使用Google Map与Excel2016开发工具进行统计,限于篇幅列出部分数据,如表4所示.
表3 运输单位计价
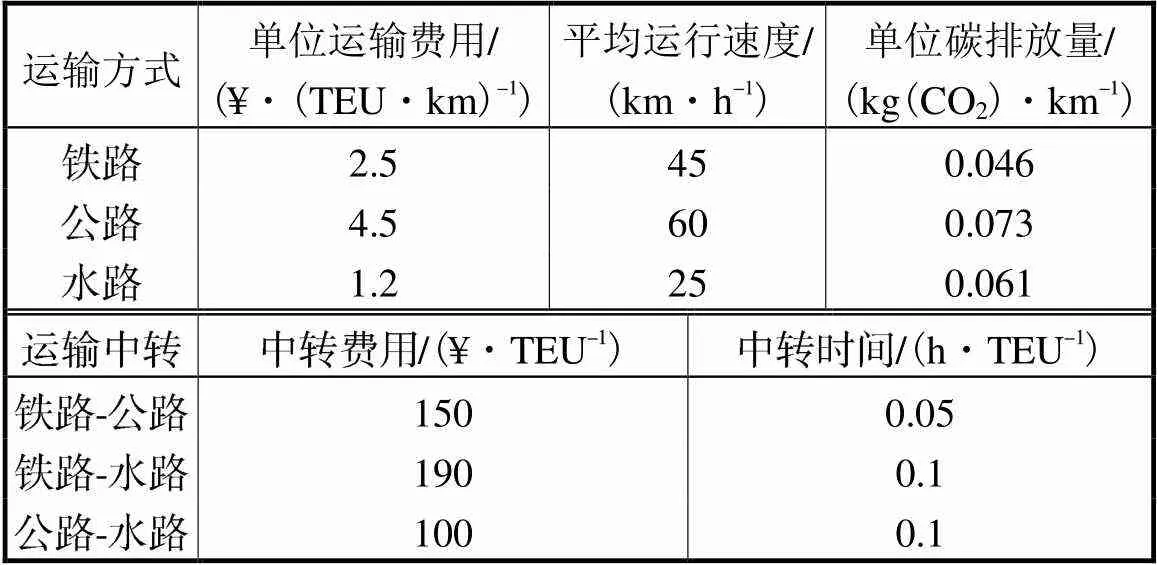
Tab.3 Freight unit valuation
表4 部分城市的交通营运里程

Tab.4 Urban node traffic operating mileage km
4.2 实验过程与结论分析
本文以机电产品的时间窗(20~28d)作为整批商品的时间窗,使用该算法对模型进行求解,得到运输方案为:郑州—保定(铁路)—天津(铁路)—圣彼得堡(铁路);重庆—圣彼得堡(铁路);上海—圣彼得堡(海运);该批次货物总运输成本为29184.90¥,时间为486.26h,碳排放量为829kg(CO2),改进烟花算法迭代47次时取得最满意,较普通烟花算法收敛速度更快,证明算法的求解效率更高,如图5所示.
4.3 敏感度分析
在上述计算过程中,本文以3种产品的时间窗中值作为整批商品的时间窗约束条件寻找最优的运输方案,在实际情况中,因不同商品的需求紧急程度不同以及公铁海3种运输方式之间的差异,客户要求的商品到达时间窗会有所不同.因此分别以上述3种商品各自的需求时间窗作为整批商品的需求时间窗,所得出的最优运输方案如表5所示.
根据表5所示,多式联运运输方案具有较强的适应性和变化性,能够满足客户对于运输方案的经济性、便捷性、绿色低碳运输等目标的追求,动态调整运输路径和运输方式.
运输方案的经济性与绿色低碳运输呈现出协同一致的变化趋势,而运输方案的经济性和绿色低碳运输均与时效性呈现出相反的变化趋势.如图6所示,由方案1到方案3,运输费用降低62.53%,碳排放量降低59.78%,而运输时间增加了346.08%.因此在实际商品运输制定运输方案时,需要综合考虑经济性与绿色低碳之间的协同变化特性以及经济性、绿色低碳与时效性之间的冲突等特性,寻求多目标之间冲突与协同之间的平衡.
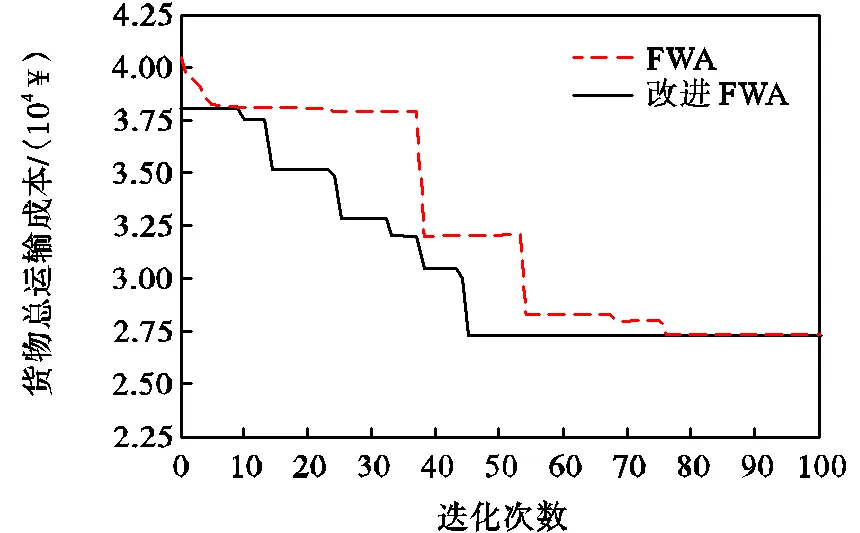
图5 寻优迭代过程
表5 不同指定到达时间情况的最优方案

Tab.5 Optimal solution with different expected arrival
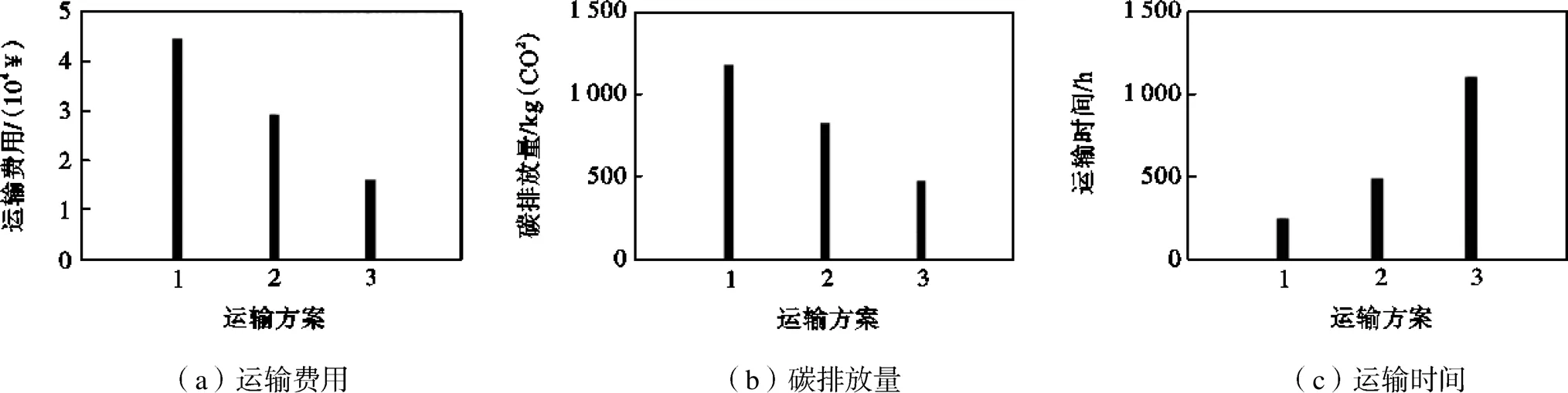
图6 最优运输方案属性对比
5 结 语
本文从中俄贸易运输现状出发,将多式联运路径优化问题与中俄实际贸易情况相结合,综合考虑不同时间窗条件下整批商品的最优运输方案,符合实际并具有数学合理性;采用改进烟花算法进行求解,通过将运输成本最小作为核心烟花的适应度函数,并控制非核心烟花的爆炸半径确保算法的全局搜索性,从而对采用烟花算法求解多目标规划问题进行了改善,提高了运行速度,改进烟花算法的收敛速度更快;通过设置3种不同的时间窗,得出不同的运输路线及运输方式,通过对比运输成本、运输时间和碳排放量,可以显著看出多式联运对于具有不同需求的商品运输而言具有良好的适应性,求解结果具有参考性.但为了便于计算,本文以3类商品中的其中一类商品的时间窗作为整批商品的时间窗,设置较为单一,在实际运输中可能存在整批商品中不同商品之间具有不同的时间窗,且要求必须在相应时间窗内送达相应的商品,因此研究同时存在不同时间窗要求的整批商品多式联运路径优化可以作为未来的研究方向.
[1] Cho J H,Kim H S,Cho H R. An intermodal transport network planning algorithm using dynamic programming—A case study:From Busan to Rotterdam in intermodal freight routing[J]. Applied Intelligence,2012,36(3):529-541.
[2] 付新平,何瑜莎,邹 敏,等. 国际集装箱多式联运线路选择研究[J]. 铁道运输与经济,2017,39(12):12-17.
Fu Xinping,He Yusha,Zou Min,et al. A study on the route selection of international container transport in the multimodal scenario[J]. Railway Transportation and Economy,2017,39(12):12-17(in Chinese).
[3] Seo Y J,Chen F L,Roh S Y. Multimodal transportation:The case of laptop from Chongqing in China to Rotterdam in Europe[J]. Asian Journal of Shipping and Logistics,2017,33(3):155-165.
[4] 李玉民,郭晓燕,杨 露. 考虑多目标的中欧集装箱多式联运路径选择[J]. 铁道科学与工程学报,2017,14(10):2239-2248.
Li Yumin,Guo Xiaoyan,Yang Lu. Route optimization of China-EU container multimodal transport considering various factors[J]. Journal of Railway Science and Engineering,2017,14(10):2239-2248(in Chinese).
[5] Hao Congli,Yue Yixiang. Optimization on combination of transport routes and modes on dynamic programming for a container multimodal transport system[J]. Procedia Engineering,2016,137(7):382-390.
[6] Qu Yi,Bektaş Tolga,Bennell Julia. Sustainability SI:Multimode multicommodity network design model for intermodal freight transportation with transfer and emission costs[J]. Networks & Spatial Economics,2016,16(1):303-329.
[7] Baykasolu A,Subulan K. A multi-objective sustainable load planning model for intermodal transportation networks with a real-life application[J]. Transportation Research Part E:Logistics and Transportation Review,2016,95(6):207-247.
[8] Chang T S. Best routes selection in international intermodal networks[J]. Computers & Operations Research,2008,35(9):2877-2891.
[9] 汤银英,戴炜东,陈 思. 考虑多节点时间窗差异的集装箱多式联运路径选择研究[J]. 交通运输工程与信息学报,2020,18(1):34-42.
Tang Yinying,Dai Weidong,Chen Si. Container multimodal transport route planning considering the difference in a multi-node time window[J]. Journal of Transportation Engineering and Information,2020,18(1):34-42(in Chinese).
[10] 万 杰,魏 爽. 基于混合算法的多目标多式联运路径选择问题研究[J]. 天津大学学报(自然科学与工程技术版),2019,52(3):285-292.
Wan Jie,Wei Shuang. Multi-objective multimodal transportation path selection based on hybrid algorithm [J]. Journal of Tianjin University(Science and Technology),2019,52(3):285-292(in Chinese).
[11] 魏 众,申金升,黄爱玲,等. 多式联运的最短时间路径-运输费用模型研究[J]. 中国工程科学,2006,8(8):61-64.
Wei Zhong,Shen Jinsheng,Huang Ailing,et al. Research on model of the shortest time path and transport cost in multimodal transportation[J]. Engineering Science,2006,8(8):61-64(in Chinese).
[12] Demir E,Burgholzer W,Hrušovský M,et al. A green intermodal service network design problem with travel time uncertainty[J]. Transportation Research Part B:Methodological,2015,93(7):789-807.
[13] Wang Xinchang,Meng Qiang. Discrete intermodal freight transportation network design with route choice behavior of intermodal operators[J]. Transportation Research Part B:Methodological,2017,95(8):76-104.
[14] 谭 营,郑少秋. 烟花算法研究进展[J]. 智能系统学报,2014,9(5):515-528.
Tan Ying,Zheng Shaoqiu. Research progress of fireworks algorithm[J]. Journal of Intelligent Systems,2014,9(5):515-528(in Chinese).
[15] 刘俨后,麻 娟,左敦稳. 基于改进烟花算法的随机装配线混流调度[J]. 控制与决策,2019,34(4):751-758.
Liu Yanhou,Ma Juan,Zuo Dunwen. Mixed-model sequencing of stochastic assembly line based on improved fireworks algorithm[J]. Control and Decision,2019,34(4):751-758(in Chinese).
[16] 安炳合,寇佳禹,王永骥. 基于改进烟花算法的多导弹目标分配方法[J]. 弹箭与制导学报,2020,40(3):113-118.
An Binghe,Kou Jiayu,Wang Yongji. A multi-targrts allocation method based on improved fireworks algorithm[J]. Journal of Projectiles,Rockets,Missiles and Guidance2020,40(3):113-118(in Chinese).
[17] 方柳平,汪继文,邱剑锋,等. 具有学习因子的动态搜索烟花算法[J]. 计算机科学与探索,2017,11(3):491-501.
Fang Liuping,Wang Jiwen,Qiu Jianfeng,et al. Dynamic search fireworks algorithm with learning factor[J]. Journal of Frontiers of Computer Science & Technology,2017,11(3):491-501(in Chinese).
Optimization of Multimodal Transport Route of Chinese and Russian Commodities Based on Improved Fireworks Algorithm
Wan Jie,Long Yunfei,Chen Xinghan
(School of Economics and Management,Hebei University of Technology,Tianjin 300401,China)
With the in-depth implementation of the“one belt and one road” initiative,the bilateral trade between China and Russia shows a trend of steady growth. The increasing demand for commodities and the diversification of the demand time have led to a significant change in the mode of transportation of commodities,from the original single mode of transportation to the present multimodal transport. The construction of a comprehensive transportation scheme through the multimodal transport means can meet the surge of commodity demand and the diversification of the commodity demand time;it can also complement the advantages of different modes of transport. To solve the optimization problem of multimodal logistics route,this paper takes the transportation route and mode of transportation between China and Russia as the research object. This paper comprehensively considers the commodity types,demand characteristics and transportation modes in the trade region between China and Russia,and establishes a multi-objective optimization model with transportation cost,transportation time and carbon emissions as the optimization objectives. Aiming at the actual situation of transportation between China and Russia,this paper considers only the multimodal transport between public transport,railway transport and sea transport,and an improved fireworks algorithm (FWA) for solving the model is design,considering the randomness and implicit parallelism of the model. By taking the multi-category commodity transportation between China and Russia as an example,the Pareto non-inferior solution of the multimodal transport route and the corresponding transportation cost,transportation time and carbon emissions are obtained,and compared with the basic FWA. The effectiveness of the model and the improved algorithm is verified. Moreover,this paper takes transport time as the sensitivity analysis variable to analyze the variation trend of transport scheme considering the attributes of transport cost,transport time and carbon emission under different time demands. This study can provide decision-making reference for the development of multimodal transport logistics between China and Russia.
comprehensive transportation;changes in demand;multimodal transport;improved fireworks algorithm
U116.2
A
0493-2137(2022)03-0291-08
10.11784/tdxbz202008086
2020-08-29;
2020-09-21.
万 杰(1972— ),女,博士,教授,jeanwan1218@163.com.
龙云飞,18406509701@163.com.
河北省军民融合发展研究课题重点资助项目(HB19JMRH020);河北省社会科学发展研究课题(2019031201028).
Supported by the Key Research Program of Hebei Province Military and Civilian Integration Development Research Project(No.HB19JMRH020),the Social Science Development Research Project of Hebei Province(No.2019031201028).
(责任编辑:田 军)

