基于ANSYS Workbench的双圆弧齿轮的动力学与疲劳寿命分析

唐 伟 袁新梅 占 凯 杨志超

（长江大学机械结构强度与振动研究所，荆州 434023）

随着工业的不断发展，在石油、煤矿等行业需要满足重载、高速、大功率的传动需求[1-2]。齿轮传动作为应用最广泛的传动形式，很难达到高性能的传动要求，传统的渐开线齿轮传动方式很难满足。双圆弧齿轮齿廓啮合方式为凸凹点啮合，相比其他齿轮传动有较高的曲率半径，因此具有较高的齿轮接触强度。双圆弧齿轮的主要参数设计灵活，可以根据不同的应用条件合理调节参数，具有齿面磨损小、传动效率高等特点[3-4]。但是，在高速、重载等恶劣条件下，齿轮构件在不同的周期循环载荷作用下极易发生齿面接触疲劳失效。因此，准确分析和预测在不同载荷作用下齿轮的接触疲劳寿命显得至关重要[5-7]。

本文以《双圆弧圆柱齿轮基本齿廓》（GB/T 12759—1991）要求的双圆弧齿轮为研究对象，结合某油田的实际工况，分析不同工况下双圆弧齿轮的接触疲劳寿命，利用ANSYS软件对齿轮进行静力学与瞬态动力学仿真分析，再利用Ncode软件并结合ANSYS的结果分析预测齿轮的疲劳寿命。

1 双圆弧齿轮模型建立

双圆弧基本齿廓由凸齿圆弧、过渡圆弧、凹齿圆弧以及齿根圆弧4段圆弧组成。双圆弧基本齿廓再通过镜像和阵列可得到完整的齿廓。在SolidWorks中绘出双圆弧圆柱齿轮，如图1所示[8-10]。本文齿轮参数如表1所示。

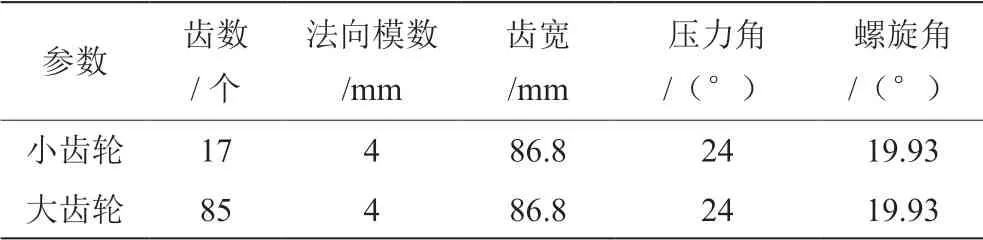
表1 齿轮参数

图1 双圆弧齿轮三维模型

2 双圆弧齿轮有限元分析

本文采用Workbench软件对齿轮模型进行有限元分析，分析齿轮在静态动力学和瞬态动力学不同条件下的接触变化情况。根据实际情况，双圆弧齿轮模型材料选为42CrMo，参数如表2所示。

表2 材料属性

2.1 静态动力学模型有限元分析

静态动力学分析时，采用Workbench中的Static Structural模块对齿轮装配体模型实现。为了加快计算机的求解效率，对双圆弧齿轮模型进行简化处理。网格划分后的模型，如图2所示。

图2 网格模型

以不同的扭矩与静摩擦系数大小作为影响齿轮疲劳寿命的主要影响因素，通过改变齿轮副不同的接触设置与边界条件，得到在静态分析下不同条件对齿轮接触应力的影响，结果如表3所示。

表3 有限元静态分析结果

结果可知，齿轮最大接触应力出现在凸齿面与凹齿面接触的地方。通过设置不同的边界条件可以发现，当不改变齿轮副的摩擦接触系数时，齿面最大接触应力大小会随着负载扭矩改变而变化。当负载扭矩变大时，最大接触应力也会变大，但没有超过所给材料的强度极限。当不改变齿轮的负载扭矩时，改变静摩擦系数大小对齿轮最大接触应力产生影响较小。该结果可探究不同的影响因素对齿轮疲劳寿命的影响规律，并可以给出影响齿轮疲劳寿命的主要影响因素。

2.2 瞬态动力学模型有限元分析

瞬态动力学分析采用Workbench中的Transient Structural模块对齿轮装配体模型进行动力学分析。根据齿轮副运动状况，对小齿轮和大齿轮设置与大地连接的转动副。先使齿轮副进入匀加速阶段，并在大齿轮上施加与大齿轮旋转方向相反的负载扭矩，这一步时长设置为0.001 6 s。再使齿轮副进入匀速运动阶段，使小齿轮转速稳定。大齿轮负载扭矩保持1 750 N·m。选择有摩擦接触，静摩擦系数为0.10。设置初始时间步长为25步，一步时长设置为0.038 4 s。需要注意，求解过程需打开大变形开关。齿轮接触面接触应力曲线，如图3所示。

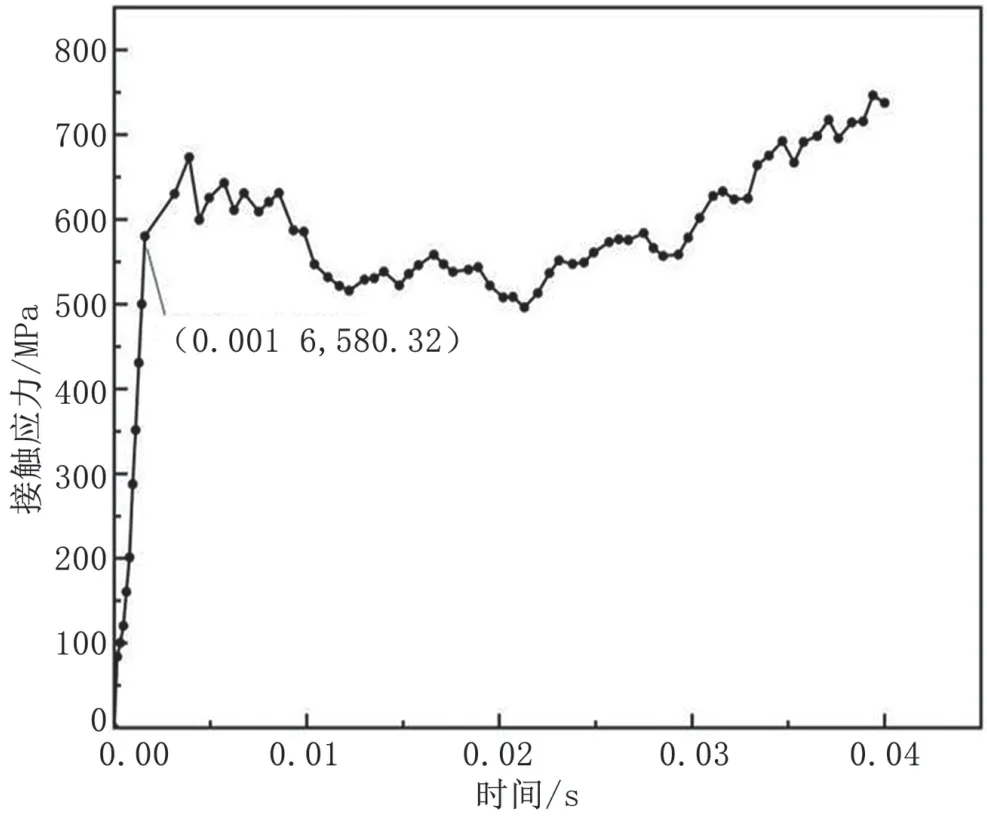
图3 瞬态动力学接触应力曲线

分析图3可知：在齿轮啮合的过程中，0 s到0.001 6 s整个系统处于匀加速状态，接触应力从0 MPa增加到580.32 MPa；0.001 6 s到0.04 s整个系统处于匀速阶段，齿轮处于相对平稳的啮合状态，接触应力在500～750 MPa变化。

3 双圆弧齿轮疲劳寿命预测

3.1 载荷谱建立

静载动力学分析不需要设置时间步。在用Ncode软件进行疲劳寿命分析时，需要定义载荷谱。静载动力学的分析结果可以映射为疲劳预测条件，为

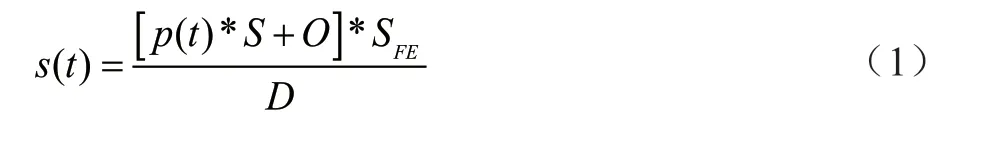
式中：s(t)为疲劳计算中使用的时间历程应力，即应力幅，对应材料S-N曲线的纵坐标值；p(t)为与时间相关的输入载荷谱，本文给用的载荷谱幅值为1，周期为0.4 s；S为比例系数，默认值为1；O为偏置，默认值为0；D为总载荷的比例控制量，默认值为1；SFE为静态动力学分析得到的有限元结果。时间序列载荷映射与有限元结果结合，得到齿轮材料的应力幅。因为瞬态动力学所得应力结果与时间有关，所以再用Ncode进行疲劳寿命预测时无须设置载荷谱。

3.2 静载动力学下疲劳寿命预测结果

在使用Ncode软件进行静载条件下预测疲劳寿命时，通过导入有限元数据、添加载荷谱、材料属性添加、求解引擎设置以及结果输出等，得到双圆弧齿轮副在静载条件下的疲劳寿命分布云图，如图4所示。

图4 静态动力学下疲劳寿命预测图

由寿命预测图可知，疲劳寿命最小区域发生在凸齿与凹齿接触面，即接触应力最大的地方。在对称循环载荷的作用下，该区域容易发生疲劳损伤，与静载动力学分析结果相吻合。

为对比不同工况下的疲劳寿命，以影响齿轮疲劳寿命主要影响因素为变量，改变仿真分析的设置，得出圆弧齿轮最小疲劳寿命的变化规律，在对称循环载荷的作用下得到双圆弧齿轮在不同边界设置下的疲劳寿命，如表4所示。

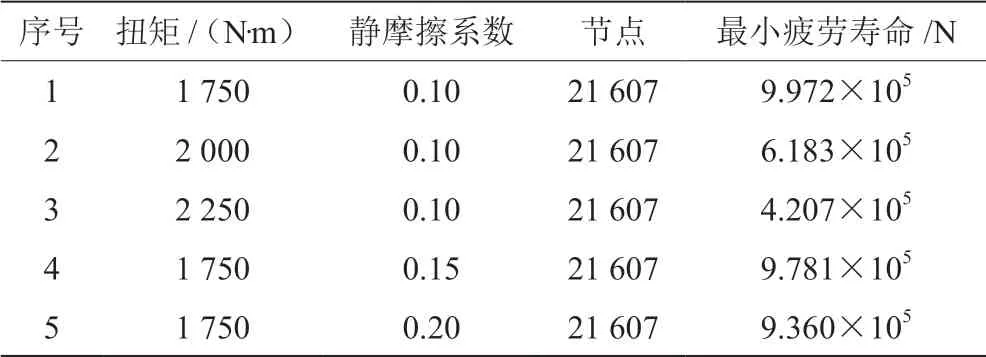
表4 静态动力学下疲劳寿命分析结果

结果可知：当静摩擦系数为0.10时，齿轮副的最小疲劳寿命随着扭矩增大会减小，且影响程度较大；当扭矩为1 750 N·m时，增大静摩擦系数，齿轮副的最小疲劳寿命减小，但影响程度较小。该规律与静态动力学在不同接触条件与边界条件下有限元分析规律相吻合。

3.3 瞬态动力学下疲劳寿命预测结果

在分析动载条件下的疲劳寿命时，与静载相比不用输入载荷谱，直接将有限元结果与Ncode连接，设置材料属性和求解设置，得到双圆弧齿轮副在动载条件下的疲劳寿命分布云图，如图5所示。

由寿命预测图可知，在当前的接触关系和边界条件约束下，齿轮副最小疲劳寿命出现在齿轮啮合处，最小疲劳寿命为41 770次。由此可知，动载情况下双圆弧齿轮的最小疲劳寿命与最大接触应力位置整体保持一致。

为对比不同工况下的疲劳寿命，以齿轮耐久性主要因素为表征参量，设置不同的接触条件与边界条件，得出圆弧齿轮寿命的变化规律，得到双圆弧齿轮在不同情况下同一节点的疲劳寿命，如表5所示。

表5 瞬态动力学下疲劳寿命分析结果

由表5的1、2、3可知：在静摩擦系数恒定时，与初始扭矩1 750 N·m相比，扭矩每增加250 N·m，即增加14.2%，疲劳寿命下降62%、85%；由1、4、5可知，在扭矩恒定时，与初始静摩擦系数0.10相比，静摩擦系数每增加50%，疲劳寿命下降16%、56%。由此分析可知，在动载条件下，扭矩对疲劳寿命的影响比静摩擦系数对疲劳寿命的影响大。

4 结论

（1）双圆弧齿轮在进行齿轮接触啮合时，无论是静态动力学分析还是瞬态动力学分析，最大接触应力都出现在齿轮啮合处，主要原因在于双圆弧齿轮啮合方式为点啮合，使得接触区域呈现椭圆形，造成齿轮的啮入位置和啮出位置接触面积较小，应力较大。

（2）对于双圆弧齿轮的静载疲劳寿命和动载疲劳寿命，根据两种载荷谱的设置，确定了在静载和动载条件下齿轮副的最小疲劳寿命出现的区域，并且根据疲劳耐久主要影响因素，得出了静载和动载下的疲劳寿命规律。