基于时域特征的风机轴承PSO-RBF故障诊断

张延琛

（山东中烟有限责任公司济南卷烟厂，济南 250000）

风能作为一种可持续能源，在世界范围内得到了广泛利用和开发。风机将风能转化为机械能，并最终转化为电能，但是在长时间运行后很容易发生故障，尤其是在恶劣环境中工作时。轴承故障是风力发电机组的常见故障之一。轻微故障可能会降低风力涡轮机的工作效率，而严重故障可能会导致灾难性后果。因此，有必要对风机轴承进行状态监测与故障诊断，确保其能够安全运行[1-2]。

风机轴承故障诊断过程主要包括特征提取和模式识别。关于特征提取，文献[3]采用小波包对振动信号进行分解重构，提取风机轴承状态特征；文献[4]在处理振动信号后，对频域特征进行提取；文献[5]以原始风机轴承振动信号为基础，计算多尺度模糊熵，获取故障特征向量；文献[6]采用改进的经验模态分解获取振动信号的不同分量，应用自回归模型提取风机轴承运行状态特征；文献[7]应用聚合模态分解与能量算子，获取风机轴承振动信号的瞬时频率和包络信号。上述风机轴承状态特征提取研究处理过程较复杂，时间复杂度高，可直接从风机轴承原始振动信号中提取时域特征分析风机轴承的故障状态。关于模式识别，风机轴承故障诊断方法包括XGBoost算法、极限学习机（Extreme Learning Machine，ELM）等[8]。风机轴承故障种类和故障程度少，因此分类器对风机轴承运行状态识别效果提出了更高要求。

为提高风机轴承故障诊断精度，提出了基于振动信号时域特征提取的风机轴承故障诊断方法。首先，直接提取风机轴承振动信号的时域特征，构建风机轴承运行状态识别所需的特征向量；其次，对获取的时域特征进行可分离性验证；最后，经对比实验验证所提方法的有效性。

1 PSO-RBF原理

径向基（Radial Basis Function，RBF）神经网络可以无限逼近非线性复杂函数，具有网络结构简单和易于训练的优点。RBF神经网络由输入层、隐含层和输出层3层组成，如图1所示。输入层是一组源节点，将网络连接到环境。隐含层神经元的激活是通过计算其中心向量和激活输入层产生的向量之间的距离来确定的。输出层是一组求和单元，提供网络的响应。

图1 RBF神经网络结构图

具有高斯函数线性组合的径向基函数网络形式为

式中：||·||为欧几里得范数；μp、σp、wi,p和yi分别为隐含层中第p个神经元的中心、宽度、输出层中的权重和第i个网络输出；P为隐含层中的神经元数。如果隐含层的中心和宽度设置适当，则RBF神经网络是泛函数近似器。径向基函数的个数影响RBF神经网络的性能，因此如何有效确定网络结构是训练中的重要问题之一。

为了获得最优的网络拓扑，提出了将粒子群优化（Particle Swarm Optimization，PSO）算法和RBF神经网络相结合的混合训练方案。PSO优化是一种基于种群的随机优化技术。PSO优化算法模拟生物的社会行为，描述一个自动进化的系统。在PSO优化算法中，每个候选解被视为n维空间中的无穷小粒子，粒子i的位置和速度矢量分别表示为Xi(t)=[Xi1(t),Xi2(t),…,Xin(t)]和Vi(t)=[Vi1(t),Vi2(t),…,Vin(t)]。所有粒子均通过拟优化的适应度函数进行评估。移动过程中，每个粒子根据自身经验和相邻粒子的经验获取最佳位置。

粒子移动遵循的规则为

式中：c1、c2和w分别为加速度系数和惯性权重；向量Pi=[Pi1,Pi2,…,Pin]为粒子i的最佳先前位置（给出最佳适应值的位置），称为最佳位置pbest；矢量Pg=[Pg1,Pg2,…,Pgn]为所有粒子中最佳位置粒子，被称为全局最佳位置gbest；参数r1和r2分别为均匀分布在[0，1]上的两个随机数；通常Vid的值限制在区间[-Vmax，Vmax]内。

PSO算法已被应用于优化RBF神经网络的各个方面，如网络连接、网络结构等。网络训练的目的是确定隐含层单元的数量、中心、宽度以及连接隐含层和输出层的权重。由于RBF神经网络的性能主要取决于隐含单元的中心，只需将这些中心编码为一个个体进行随机搜索，进一步分别通过启发式和解析方法确定宽度和权重。为了充分利用PSO优化算法的潜力，采用实值标志用于指示网络中是否涉及相应的隐含单元。因此，粒子的结构由标志和隐含中心的串联表示，如图2所示，其中hmax为隐含单元的最大数量。

图2 粒子位置结构

如果标志i＞0，则第i个隐含单元包括在网络中；否则，将第i个隐藏单元从网络中删除。通过这种方式，粒子可以被解释为具有可变隐含单元数的网络。第i个隐藏单元的宽度由启发式公式确定，即

式中：h为网络中涉及的隐含单元数。通过使用最小均方算法最小化网络的平方误差确定权重。RBF参数的粒子值用k均值算法获得初始化值。每个粒子的适应度值是网络和期望输出之间的均方误差值。

2 时域特征提取与故障诊断流程

2.1 风机轴承数据集简介

风机轴承故障诊断研究所需的数据集选自某实际风电场，包含近3年的主轴承振动信号。采集数据集时，采样频率是1 200 Hz。在轴承内圈、外圈和滚动体上设置不同故障程度单点故障，损伤直径分别为0.177 8 mm、0.355 6 mm、0.533 4 mm。滚动轴承内环、滚动轴承外环、滚动体各有3类故障状态，另加正常状态共分为如表1所示4类主轴承故障状态。各损伤直径采集900 000个采样点，并且每个样本由1 000个连续采样点组成。当诊断风机轴承故障时，样本按照4∶1的比例分成训练集和测试集。

表1 主轴承故障状态分类

2.2 时域特征提取

在诊断风机轴承故障时，获取有效的轴承运行状态特征至关重要。在提取特征时，为提升特征提取效率和降低信号处理的复杂度，直接获取风机轴承运行状态的时域特征。风机轴承故障诊断研究所需的时域特征计算公式如表2所示。

表2 特征计算公式

2.3 风机轴承振动信号特征分析

对风机轴承的原始振动信号进行时域特征提取后，对每种风机轴承运行状态各取一组进行特征分布分析，分析结果如图3所示。从图3展示的分析结果可以看出，风机轴承的不同运行状态所包含的特征存在差异。获取的时域特征具有良好的类可分性，可输入到风机轴承运行状态分类器中分类。

图3 特征向量分布

由于不同时域特征对分类结果的影响程度不同，选择的特征个数过多或过少都将影响最终的风机轴承故障准确率。为了避免特征维数对风机轴承故障诊断结果的影响，需要对17维时域特征进行特征选择。先获取各时域特征的特征重要度，将17维时域特征按照特征重要度按照由小到大的顺序进行排列（图4展示了重要度较大的前10维时域特征）。将各特征按照特征重要度进行排序后，按照特征重要度由大到小依次增加风机轴承故障诊断模型输入特征的维度。同时，以分类准确率为判断依据，当分类精度出现拐点时对应的特征维度即为最优特征子集维度，包含的特征即为最优特征子集。

图4 特征重要度值

表3中展示了3种不同分类器的特征选择结果，其中XGBoost、ELM和PSO-RBF最优特征子集维度分别为7、13和12。在特征选择过程中，3种分类器各模型的最高准确率分别为96.59%、97.23%和98.79%，初步说明了PSO-RBF分类器的优越性。同时，图5对XGBoost、极 限 学习 机（Extreme Learning Machine，ELM）和PSO-RBF这3种分类器的特征选择过程进行了展示。

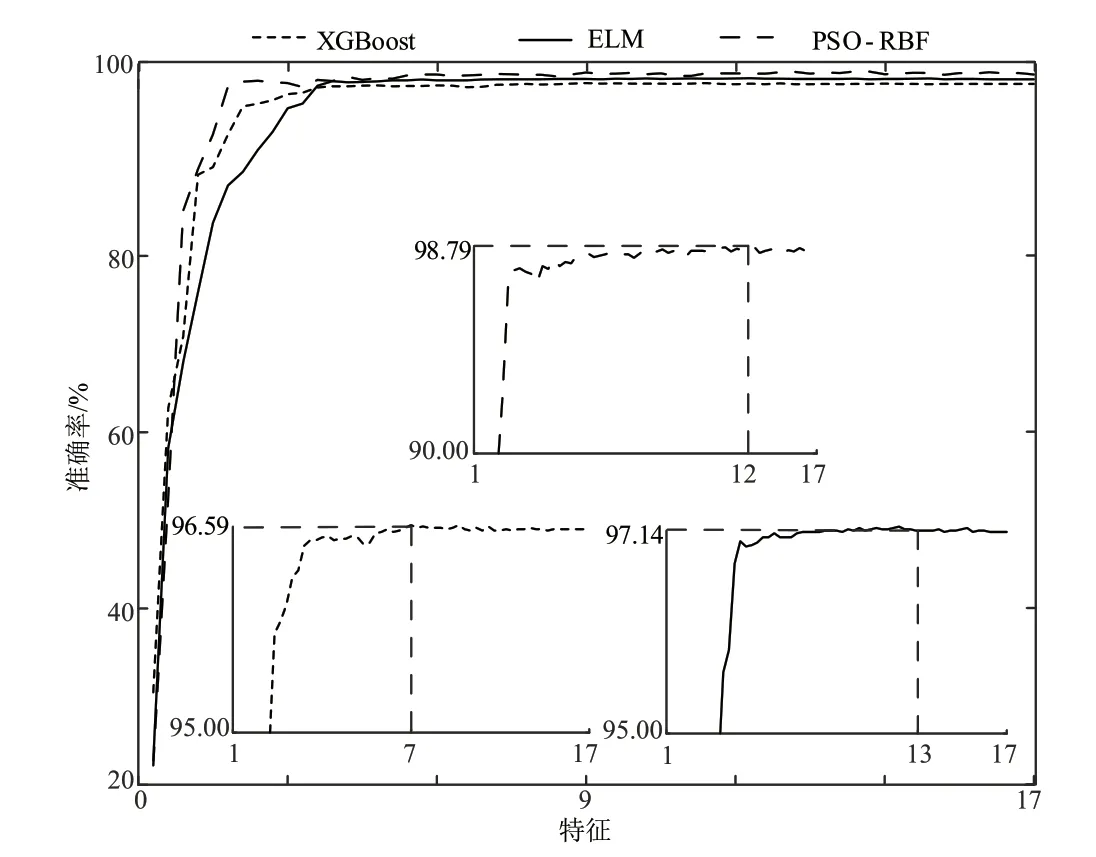
图5 不同分类器特征选择过程对比

表3 特征选择结果

3 算例分析

为了验证提出的基于PSO-RBF神经的风机轴承故障诊断模型的有效性，与XGBoost和ELM模型开展对比实验。XGBoost和ELM模型的训练集与测试集与提出方法设置相同。将测试集中风机轴承故障诊断的最优特征子集输入到训练完成的3种分类器后，获取到各模型的故障诊断分类结果。3种分类器的风机轴承故障诊断结果的混淆矩阵，如图6所示。为了进一步将故障诊断结果可视化，不同分类器的状态识别结果统计在表4中。

从图6和表4中展示的分析结果可以看出：XGBoost模型的每种类型故障识别准确率高于95.3%；ELM模型的每种类型故障识别准确率高于96.3%。相较于对比模型，提出的PSO-RBF模型的每种类型故障识别准确率高于98.2%。可见，所提方法具有有效性。

图6 3种分类器故障诊断结果

表4 不同分类器状态识别结果

4 结论

为了提升风机轴承故障诊断的特征提取效率和故障识别的准确性，提出了基于时域特征的风机轴承PSO-RBF故障诊断方法。提出的故障诊断方法主要具有如下优点：

（1）直接获取风机轴承原始振动信号的时域特征，高效刻画风机轴承的不同运行状态特征，有效提高了风机轴承故障诊断效率；

（2）将PSO-RBF模型引入风机轴承故障诊断，并优化相关参数，证明相较于传统的XGBoost和ELM分类器，PSO-RBF模型具有更优的性能。