基于Cohen-Sutherland编码理论的光栅信号数字细分算法研究

王朝峰 张 玉 林江海

（山东省机械设计研究院，济南 250031）

光栅是一种高精度测量仪器，被应用于高精度加工、检查以及坐标方向测量。莫尔波纹是一种以光栅的相对移动为基础的技术。因为该光栅的相对运动，传输光的光强会周期性改变。该光强信号被硅光单元转换成具有周期变化的电子信号（正弦波），并在一组信号中进行一组处理，从而得到该光栅的相对位移。然而，单靠对其周期的估算远远无法达到准确的检测要求。在计算机技术快速发展的今天，对莫尔条纹进行高阶、高精度数字分割已经势在必行。

数字化分割技术是一种新的、行之有效的方法，是目前国内外学者关注的一个热点问题。当前，常用的数值划分技术多采用软件实现，如将“插值”与“四边形”相结合，利用数学模型建立新的曲线方程式程[1-3]，即纯粹的硬件划分[4-5]。然而，这些技术中的细分技术数目较小（通常是500以下）且线路较多，容易造成信号干扰，影响有效信号。由于资料的准确性下降，资料加工困难，很难达到较高的解析度。

文中使用计算机软件中的“大号”和“细分小号”相结合的方法进行划分[6]。在细分方面，利用分段运算和正余切功能，既能提高分辨能力，又能保持线性特性。该方法利用快速计时器芯片进行运算，而小数运算通过软件的分解来实现。莫尔条带循环可逆算，而小数计数法则是莫尔条带细分的一个周期。本文以光栅微机上的软件为对象，在此基础上利用Cohen-Sutherland编码原理对相位划分进行详细的分析[7-8]。

1 数字细分理论

光栅测试装置是利用光栅法实现对输入量（位移、角度等）进行变换和输出的一体化测试装置。光栅测光的基本原理是利用光栅对来自光源的光进行调制，把机械位移量转化为光学信号，并将其转化为可根据光线的调制而改变的交流电信号。通过不同的加工、转换，可以对不同的力学、形位进行对应的检测。在测定长度时，光栅是以间隔W为单位的编码标尺。如图1所示，编码标尺的同时，利用光栅作为基准进行对比和测定，可以从被测物体上读出X，表达式为

图1 光栅精密测量定位原理

式中：N为AB间的光格计数；δ、δ1、δ2分别为在AB两端对应的光格上读取划分的小数值。

可见，栅格的测量本质上是相应的格线N个数和少于节距的点数的总和。

如果测量精度允许对十进制值进行四舍五入，则可将方程式简化为

因此，光栅长度可以通过简单地读取光栅栅线的数量N获得。

如果测量精度不允许四舍五入到十进制值，则必须细分光栅间距。假设可以将间距细分为n个相等的部分，则栅格细分的分辨率为

此时，测得的小数部分为

式中：m=0,1,2,…,n。

将式（3）和式（4）代入到式（1），并令M=N·n+m，则

从而得到测量单位最小的系统方程。

实践中，若以栅格角度或栅格角度为单位，仅可求出整列间隔，其数值精确性远低于以上所提需求。为了达到要求的精确度，选取合适的栅格间隔进行划分，然后通过对间隔的划分获取最低的读出值来提高设备的解析度。需要说明的是，细分是指一条莫尔带上的多条测量脉冲。

在传统技术中，常采用细分法进行测量。该方法具有简便、信号要求低的特点，适用于静、动两种不同的测量方式，但划分数目较少。移位电阻链法是一种比较精细的测量方法，但是电路比较烦琐，信号的正交性很强，且测量的准确率受到零漂的限制。振幅分裂电阻链方法具有精确性好的优势，不会受到信号的幅值和振幅的影响，可以实现动静两方面检测，但是线路比较烦琐。锁相细分法具有细分数量大、电路简单以及信号不严谨等优点，只适用于动态检测，但均匀性好，光栅运动高。载波法具有较大的细分能力和较高的准确率，但是线路比较烦琐，同时其波形学和正交度比较高。

从上述结果可以看到，在需要进行大规模划分时，若采用硬体划分，将会造成较大的困难，并不适合于单纯的硬件实施。莫尔条形码的划分是利用计算机程序对其进行划分，再利用程序划分，即利用采集与储存的资料将莫尔条纹的两个相位为90°的脉冲输出信号进行数字化处理，并进行多次波形和数码展示。利用计算机软件细分，可以使装置的硬件结构更加简单，降低线路对有效信号的干扰，加强装置的性能，改善装置的准确度。

2 数字细分算法

如图2所示，莫尔条带在理论上并非正弦脉动，而在槽宽为W/2（也就是代表光栅的光透过部）和空隙为0时得到三角波形。然而，在现实的构造中，光栅的信号会改变。光束的不均匀性和光的衍射效应，光罩面间光的反射，光栅光罩的凹凸不平等，均会改变光栅信号，变化曲线接近图3。

从图3可以看出，在出相与暗相的光发射端，一个正弦波的信号被光器件生成。从图2可以看出，按照光电变换的原则，光学信号被变换成电信号，此时仍然是正弦信号，可以用一个正弦波来代表

图2 光栅理想信号

式中：U为光电元件输出信号；W为光栅栅距；X为位移；Up-p为信号峰值；Ucp为直流电平。

与图3相似，在光器件收到明暗色的正弦信号后，按照光电变换的原则，把该光学信号变换成电信号仍然是正弦波，也可以由式（6）来表达这个正弦波。

图3 光栅实际信号

通过计算、区分、细分和小数计数等全周期，采用相角偏差90°的正弦型和余弦型进行测量。在幅度调节时，真实的信号U的幅度会随着电源波动、光强度和光栅间距而变化。但是，由于气温等环境因素的作用，系统无法获得精确的变形信息。

分析表明，当两路莫尔条纹的振幅改变相同时，振幅U的波动效应可以用莫尔条带的正弦和余弦比例来抵消，即这里U为振幅，θ为相位角度，由此确定位移。

在两个莫尔条带的幅度改变相同的条件下，可以用莫尔条带的正弦与余弦之比排除幅度U起伏的效应，并隐藏一定的位移量。这样可以根据得到的数值获得相位角，进而得到相应的位移量。

以sin光栅信号与cos栅极信号的过零及其绝对等效处为界，将一栅格循环划分为8个具有相位角度的区，并将8个区的基础设为0、100、200、300、400、500、600以及700（此处是800个划分实例，实践中如果有必要，可以在该方案中增加划分倍数），见图4[9]。

图4 细分原理图

利用以上划分原则，将一个周期（0°～360°）的正弦波信号划分为8个区间，各分区使用三位二值码，右侧为首位[7]。假设每一次获得的两个测量信号的数值是Usin、Ucos，编码规则为：若Usin＞0，则第1位置1，否则为0；若Ucos＞0，则第2位置1，否则为0；若|Usin|-|Ucos|＞0，则第3位置1，否则为0。

根据该编码规律，可以方便地求出各基元的编码数值，方法如表1所示。

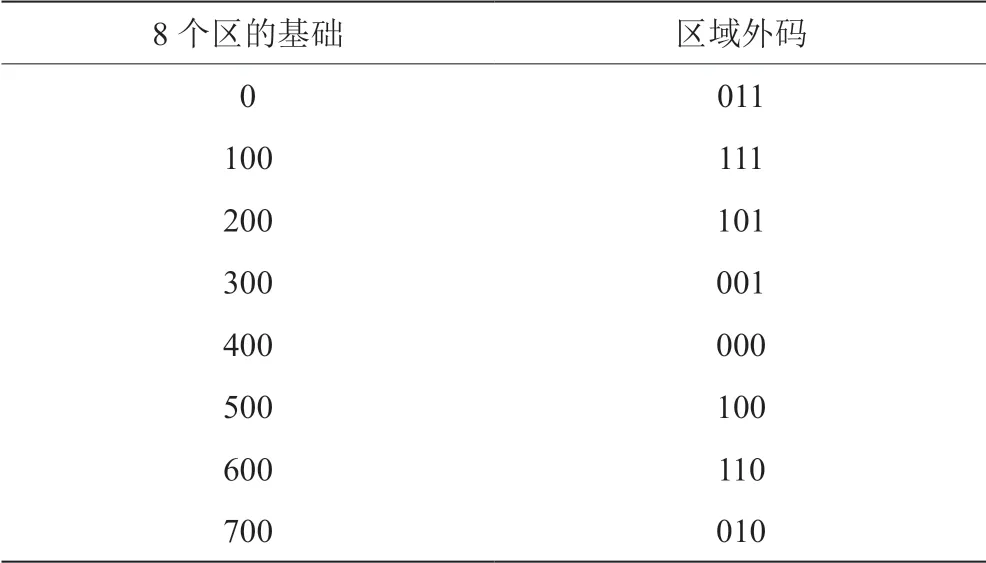
表1 区域外码

相位角分成8个区域后，由三角函数图像和性质可以得到区域外码判别的方法，如表2所示。外码中的每一位被置成1（真）或0（假），就能得到对应区域三位二进制代码。

表2 区域基数与外码对应表

由编码规则很容易得到每个基数对应的编码值。基于Cohen-Sutherland编码理论的相位角区域编码算法具体步骤如下。

步骤1：定义一个含有4个成员变量的类CCode，成员变量为all、sin、cos、sc。

步骤2：完成编码。

步骤2-1：初始化CCode对象的成员变量all、sin、cos、sc分别为0；

步骤2-2：获取测量信号值Usin、Ucos；

步骤2-3：如果Usin＞0，sin=1，否则sin=0；

步骤2-4：all+=sin；

步骤2-5：如果Ucos＞0，cos=1，否则cos=0；

步骤2-6：all+=cos；

步骤2-7：如果|Usin|-|Ucos|＞0，sc=1，否则sc=0；

步骤2-8：all+=sc。

步骤3：输出编码结果。

以表1中的区外代码为基础，识别获取的数据，即寻找一个地区基础数值，然后把该地区的基础值和各分区的分区进行综合，将一个循环的800次分割开来。对于在任意i上的一个信号数值，相应于这个位置的一个小的数值Xi为

按下列方式运行算法，计算每次获取测量信号的外码，由循环语句判断该外码值对应的区域基数。同时，根据外码值的奇偶性，决定调用式（8）或式（9）计算对应区域的细分值。信号处理流程如图5所示。

图5 光栅信号处理流程

3 结语

从理论上研究了测量栅格的技术原理，提出了莫尔条纹细分算法。通过对通用齿形测试仪的实际使用，证明了所提方法可以对800个光栅格进行分割，50根/毫米的光栅解析仪的分辨率超过0.025 μm，具有较好的转化效率。与传统的硬件细分方法比较，它的精度可以达到1～2个百分点。试验结果表明，该控制方案性能良好，工作性能稳定，并有较好的抗噪声性能和很强的灵活性，能够根据实际需求和计算机软件实现精确划分。