基于结构信息的粗粒土抗剪强度模型研究

梁彭，魏玉峰，黄鑫，王洋，贺琮栖

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

粗粒土是自然界中广泛分布的岩土体材料，多为无胶结状态，其结构特性主要受颗粒形状、尺寸大小、排列分布以及接触咬合等因素影响。与常规细粒土相比，粗粒土具有压实性能好、透水性强、承载力高、不易变形等特点，因此常作为机场、大坝、公路等工程的路基填方材料。早期有关土体结构性的研究主要集中于细粒土，如王国欣等[1]总结归纳了黄土和软土的结构性研究现状。谢定义等[2]通过对土体结构性研究方法进行探讨和考察，提出了能够反映土体联结和排列特征的定量化指标。近年来，许多学者在粗粒土结构特性方面也开展了较多研究，如姜景山等[3]采用数值分析方法获取了剪切破坏过程中颗粒排列、位移、咬合、接触、剪切变形和颗粒破碎等组构变化信息，以组构变化信息定性或定量地分析了颗粒的运动规律；刘汉龙等[4]在综述中总结了土体结构性对颗粒破碎的影响。目前对土体结构性研究的手段主要集中为数值模拟、试验研究和理论分析3个方面。数值模拟作为辅助研究手段，通常用来获取试验过程中的组构变化现象，分析结构变化的规律性。如LIU等[5]通过离散元数值模拟方法推导了岩体键合单元参数与力学性质之间的换算公式，并在此基础上提出了能量转换规则。聂志红等[6]采用PFC2D软件模拟并分析了粗粒土孔隙特征演化规律，并对其影响因素进行了探讨。朱遥等[7]利用二次开发的高性能离散元软件MatDEM对不同形状砂土进行直剪试验过程模拟，分析了颗粒形状对砂土抗剪强度的影响；LI等[8]通过CT扫描和数字图像处理技术，结合数值模拟方法建立了土壤基质与砂砾界面线框模型。试验研究方面，由于现场原位试验开展较为困难且费用较高，现阶段的研究主要采用玻璃、金属、石膏、光弹性介质等规则、理想的代替材料开展室内模拟试验，来分析结构性对抗剪强度的影响[9]。如HAERI等[10]采用改良的室内三轴试验分析了结构和扰动对湿陷性土力学特性的影响；SHAO等[11]通过室内真三轴试验对具有裂隙的黄土强度特性进行研究，对不同方向荷载作用下黄土的破坏准则进行了探讨；张振东等[12]通过开展大型动三轴试验研究循环荷载下不同类型筑坝堆石料颗粒的破碎特性。理论分析方面，主要是建立结构与力学性质之间的本构关系。沈珠江等[13-15]考虑土体结构性本构关系，建立了弹塑性损伤模型、堆砌体模型和二元介质模型；DESAI等[16]建立了结构性土的扰动状态模型；李吴刚等[17]通过结构性因子表征土的结构性，并利用修正剑桥模型建立了考虑土结构性的本构模型。以往的研究重点一般针对黄土、膨胀土等细粒土。如谢定义等[2]建立了一个反映土结构性的指标；LI等[18]通过分析黄土的微观结构演变过程解释了微观结构特征与力学响应之间的联系。现阶段对粗粒土组构和其宏观抗剪强度的研究还缺乏深入的探讨，因此本文以粒径范围10～30 mm的无胶结卵石颗粒为对象，通过室内试验和数值模拟方法，建立表征粗粒土结构信息的综合量化指标，提出了包含结构信息的粗粒土抗剪强度模型。

1 粗粒土直剪试验结果及分析

1.1 试验设计

郭庆国[19]通过综合分析粗粒土试验数据，提出用P5表示大于5 mm颗粒含量占总质量的比值，并认为P5=30%和P5=70%是控制粗粒土强度特性的2个重要分界点。张振平等[20]将采集到的试样分为≤2 mm土样和5～10 mm碎石进行物理指标分析，并将土石阈值设定为2 mm，根据含石量阈值将含石量小于30%的土石混合体划分为悬浮密实结构，含石量在30%～70%之间划分为密实骨架结构，含石量大于70%时，为骨架孔隙结构。

因此，本文在总结前人成果基础上，为了便于开展宏观、细观的试验和数据采集，以粒径范围10～30 mm的无胶结卵石颗粒为试验对象，将其划分为悬浮密实结构、密实骨架结构、松散接触结构和骨架孔隙结构4种类型。本文选取颗粒粒径较大，以P5来描述显然不合适，因此采用P20来表征粒径大于20 mm的土颗粒含量占总质量的比值。各类型粗粒土性质分别为：悬浮密实结构P20≤30%，密实骨架结构P20为30%～50%，松散接触结构P20为50%～70%，骨架孔隙结构P20≥70%。

由于常规直剪仪不能实时观测剪切盒内部试样的变形演化特征，故将传统的中型直剪仪进行改进设计，优化后的剪切盒为有机玻璃与钢板制作而成(剪切盒尺寸为300 mm×300 mm)，具有透明可视化特点(如图1所示)。

对4种不同结构类型粗粒土试样在50，100，150和200 kPa法向应力条件下进行可视化剪切试验，试样配比信息见表1。试验过程中记录不同时刻试样的剪应力及剪切位移变化数据，分析试样的应力应变特征，并结合图像采集系统对透明剪切盒内部颗粒试样的结构状态进行观测。

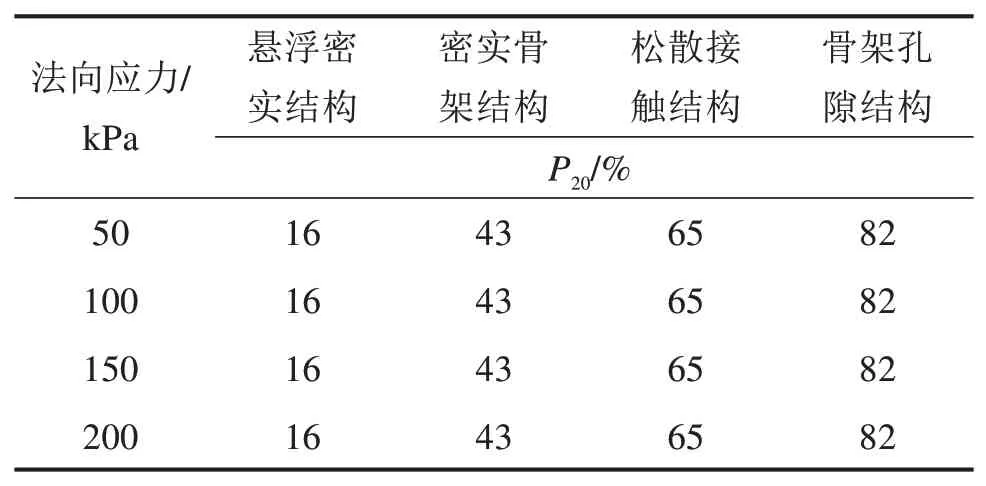
表1 试样配比Table 1 Sample proportions

1.2 试验结果分析

通过可视化直剪仪对不同结构类型粗粒土开展剪切试验，得到对应的应力-位移曲线如图2所示。由图2可知，不同结构类型粗粒土试样的应力-位移曲线存在一定差异，但整体上均表现出峰值应力与法向应力呈正相关的关系，符合土体的摩尔-库伦强度公式。在低法向荷载作用下，试样的应力-位移曲线变化趋势相对平缓，具有明显的土体硬化特征。其中，密实骨架结构(P20=43%)和松散接触结构(P20=65%)峰值剪应力明显高于其余2种结构类型粗粒土，反映出粗粒土峰值应力随着颗粒级配的变化具有一定的区间效应，即当粗颗粒土中P20含量在43%和65%时其峰值应力反而比P20含量少于43%或大于65%时高。由此可以看出粗粒土的强度效应不仅与法向应力有关，也与其自身的结构特性有一定的相关性。

2 结构信息综合参数量化指标

2.1 粗粒土结构信息指标

自然界中岩土体材料具有复杂的离散性特点，为了尽可能对土体的结构特征进行精确描述，文中重点对粗粒土颗粒的几何形状、排列分布以及接触特征等结构信息进行了提取，将扁平度、圆度、主定向角、配位数以及孔隙率作为表征粗粒土结构信息的量化指标。各指标定义如下：

1) 扁平度：指等效椭圆颗粒的长轴与短轴之比，其计算式为：式中：L为颗粒等效椭圆的长轴值；B表示等效椭圆的短轴值。

2) 圆度：用于评价不规则颗粒表面轮廓局部尖角特征(Roundness)的常见物理量，根据Image-Pro Plus软件中的IPP圆度模块，其计算公式为：

式中：S为颗粒圆度；P为不规则颗粒的最大横截面周长；A为不规则颗粒的最大横截面面积。

3) 定向角：表示颗粒排列特征的物理量。当颗粒受外力作用时其长轴会逐渐向垂直受力方向排列，此时长轴与水平轴正向夹角即为主定向角。

4) 配位数：表示试样中某个颗粒的平均接触数目[21]。它是衡量颗粒材料密实程度的一个指标，配位数越大，颗粒体系越密实；配位数越小，颗粒体系越疏松。其计算公式为：

式中：Na为颗粒总数目；n为颗粒a的接触数目。

5) 孔隙率：指颗粒间孔隙体积占总体积的比值，图3中黑色区域所占比例即为孔隙率。

2.2 粗粒土结构信息提取

由于粗粒土的结构信息会随着剪切过程不断发生变化，在后期数值模拟试验过程中也只能控制初始时刻结构信息保持一致，而难以使整个过程各指标的动态演化是一致的，因此统一选取初始时刻的结构信息指标来分析其对抗剪强度的影响。

利用数码相机记录初始时刻粗粒土形状特征、颗粒接触、排列分布等结构信息，并结合Matlab软件对图像进行预处理，随后基于Image-Pro Plus(IPP)图像处理软件的count测试手段，提取颗粒的周长、面积、扁平度、圆度、定向角等结构信息。在此基础上，应用PCAS图像识别与分析系统统计出颗粒与孔隙含量(孔隙率)，具体过程如图4所示。不同结构类型粗粒土结构信息指标汇总见表2。

表2 颗粒结构信息量化指标汇总Table 2 Summarization of quantitative indexes of structural information of coarse grained soil

2.3 结构信息综合参数指标计算

直剪试验结果表明，相同材料、级配、颗粒形状以及恒定荷载作用下的颗粒体系，受力后表现的应变特征及抗剪强度差异也较大，即粗颗粒土的抗剪强度不仅与法向应力、颗粒级配密切相关，还与颗粒体自身的接触、排列等结构特性有关。因此，本文采用多因子综合评价法，建立结构信息综合量化参数，对初始结构信息与抗剪强度之间的关系进行描述。

2.3.1 各结构指标量化权重的确定

将各个结构信息指标的加权平均和定义为结构信息综合参数。采用主成分分析法对各个指标的相关性进行分析，确定相关系数矩阵及其特征值和特征向量，根据各个指标的累计方差率确定主成分数，最后计算主成分的载荷系数(特征值的方根与对应的特征向量的乘积)，进而归一化后得到量化权重指标。

表2中获取的结构信息共包含5个初始结构指标，每个指标对应16组试验数据，将其视为A=(a1a2a3a4a5)′的容量为m=16的试验数据A1,A2, …,A16的样本观测值，然后对A的主成分元素求解。将数据标准化后在matlab中通过“zscore (A)”求得相关矩阵为：

相关矩阵的特征根分别为：λ1=0.316 9，λ2=0.507 4，λ3=0.676 5，λ4=1.328 3，λ5=2.170 9，根据式(4)和式(5)确定累计方差贡献率的主成分。

式中：G(r)为累计方差贡献率；r为主成分数。

由式(5)可知，仅需确定后面4个主成分即可，λ2，λ3，λ4，λ5所对应的特征向量和方差贡献率见表3。从表3可知，λ5方差贡献率最大，说明其综合能力最强，选用a1，a2，a3，a4，a5对应的特征值和特征向量来计算5个单因素分别所占权重，计算结果见表4。

表3 主成分所对应的特征向量、特征值及方差贡献率Table 3 Eigenvector, eigenvalue and variance contribution of corresponding principal components

2.3.2 结构信息综合参数指标计算

通过主成分分析法计算出的孔隙率、扁平度、定向角、圆度和配位数5个结构指标所占权重如表4所示，则综合参数K表示为：

表4 结构信息指标权重计算结果Table 4 Calculation results of weight of structural information indexes

式中：K为结构信息综合参数；a1为孔隙率；a2为扁平度；a3为定向角；a4为圆度；a5为配位数。

由式(6)可知，a1的系数为负值，说明孔隙率在结构信息综合参数关系式中起减值作用，孔隙率越大则K值越小，扁平度、定向角、圆度和配位数则与结构信息综合参数呈正相关，圆度对综合参数的影响最大，孔隙率和扁平度对综合参数的影响则相对较小。不同结构类型粗粒土的综合参数计算结果见表5。

表5 结构信息综合参数指标计算结果Table 5 Calculation results of comprehensive parameter index of structural information

3 嵌入结构信息综合参数的粗粒土抗剪强度模型

3.1 不同结构类型粗粒土强度特征数值模拟

在进行物理试验时，不同法向应力下剪切试样的形状、排列和接触特征都会发生变化，因此，为了保持试样结构的一致性，采用数值模拟方法来模拟整个剪切试验过程，以此来获取不同初始结构类型粗粒土的抗剪强度参数。

采用离散元分析软件PFC2D对剪切试验进行数值模拟，模拟时导入物理试验记录的结构信息图像，使数值模拟的试样扁平度、圆度、主定向角、配位数以及孔隙度等结构信息与物理试验保持一致。并选用柔性颗粒簇cluster模拟复杂颗粒的生成，颗粒间接触采用平行黏结、线性接触，通过多次试算后将物理试验中的力学参数转换为数值模拟试验中的细观参数如表6所示。

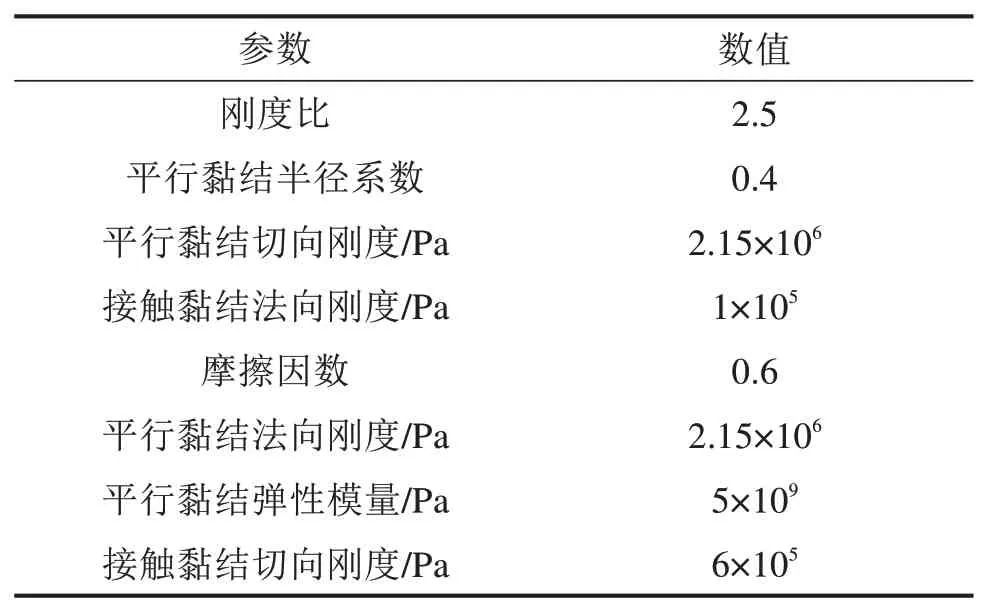
表6 模型细观参数取值Table 6 Values of mesoscopic parameters of the model

模拟的剪切盒尺寸大小为300 mm×300 mm，在剪切盒内导入由物理试验获取的真实轮廓颗粒后生成试样，使试样分别在50，100，150和200 kPa法向荷载下伺服稳定，固定剪切盒下半部分墙体，给上部墙体施加一个向右的剪切速度，从而完成试样的剪切(如图5)。

数值模拟与室内试验获取的法向应力条件下各类型粗粒土试样应力-位移曲线对比如图6所示。从图中可以看出数值模拟的结果与试验结果曲线峰值基本保持一致，因此通过数值模拟获取的强度参数具有可靠性。

陈希哲[22]通过选取砂砾石进行了粗粒土的强度与咬合力试验研究，建议采用粗粒土咬合力产生的摩阻角和结构力来代替摩尔库伦模型中的摩擦角和黏聚力，考虑咬合力作用的粗粒土抗剪强度公式如下：

式中：ψ为粗粒土咬合力产生的摩阻角；c为粗粒土咬合力产生的结构力。

根据数值模拟获取的粗粒土应力-位移曲线，利用最小二乘法拟合不同结构类型粗粒土强度特征曲线，绘制出4种结构类型粗粒土抗剪强度包线如图7所示。从图7可以看出，不同结构类型的粗粒土强度参数指标具有一定的差距。密实骨架结构具有较大的摩擦角和黏聚力，其强度参数明显高于其他3种类型粗粒土，低应力条件下4种结构类型粗粒土结构强度较为接近，随着法向应力的不断增加，峰值剪应力出现不均匀变化。4种结构类型粗粒土虽然都属于无黏性土，但都存在较大的c值，并且直剪试验条件下得到的摩擦角普遍较大。这是由于粗粒土颗粒之间会产生镶嵌咬合力，从而使土体本身的强度指标发生变化。

3.2 嵌入结构信息综合参数的粗粒土抗剪强度模型

通过试验测得的不同结构类型粗粒土对应的结构信息综合参数指标、摩阻角和结构力结果如表7所示。结构信息综合参数K与粗粒土考虑咬合力作用下的抗剪强度指标摩阻角ψ，结构力c的关系如图8所示。

表7 不同结构类型粗粒土强度参数指标Table 7 Strength parameters of coarse-grained soils with different structural types

由图8得到粗粒土结构信息综合参数K与摩阻力c，结构力ψ的关系可表示为式(8)和式(9)所示：

通过试验数据分析可发现，粗粒土的抗剪强度与其自身的结构信息有着直接关系。本文拟将结构信息综合参数K引入粗粒土考虑咬合力作用的抗剪强度模型中，以此来反映粗粒土强度特性。将式(8)和式(9)中的摩阻力ψ和结构力c用结构信息综合参数K来表示，则考虑结构信息影响的抗剪强度公式可表示为：

由于K随法向应力σ的变化而变化，因此式(10)中K为平均值，该式可以充分考虑粗粒土结构中颗粒的形状、排列和接触特性对抗剪强度的影响，从而更全面地反映不同结构类型粗粒土的强度特性。

4 强度模型可靠性分析

将Mohr-Coulomb准则计算值和本文提出的模型计算值分别与直剪试验获取的峰值应力进行对比，4种类型粗粒土基于Mohr-Coulomb准则的计算值与直剪试验值对比如图9所示。图9中深色部分为95%置信带，浅色部分为95%预测带。从图9可以看出，M-C准则计算值与试验实测值数据点基本处于95%误差带范围内，且较为紧密地分布于1:1梯度线处，拟合曲线的斜率为0.999，线性拟合系数为0.996，相关性较好。从数据点的分布情况来看，低应力段数据点大多分布于梯度线下方，高应力情况下则基本分布于梯度线上方，表明低应力条件下M-C准则计算值比实测值偏大，而在高应力状态下计算结果比实测值偏小。

图9为4种结构类型粗粒土基于本文提出的嵌入结构信息综合参数的抗剪强度模型计算值与直剪试验值对比图。图中数据点均分布于95%预测带以内，拟合曲线斜率为1.074，拟合系数为0.986，相关性较好。由图10可知，在低应力段数据点较为紧密地分布于梯度线两侧，随着应力的不断增大，数据点的分布位置逐渐分散；通过相关系数计算公式可得，低应力段(200 kPa以下)M-C准则计算值与实测值的相关系数为0.89，而本文模型公式计算值与实测值相关系数为0.95，即与Mohr-Coulomb准则相比，本文提出的模型计算值在低应力段与试验实测值有更高的相关性，数据点基本位于1:1梯度线上，表明本文提出的考虑结构信息的抗剪强度公式更适用于低应力条件下粗粒土强度特性的表征。

5 结论

1) 依托可视化直剪试验，分析了4种不同结构类型粗粒土宏观抗剪强度特性，获取了各结构类型粗粒土的扁平度、圆度、主定向角、配位数和孔隙率等结构信息指标，采用主成分分析法量化这5种影响因素所占权重，建立了粗粒土结构信息综合参数指标K。

2) 通过数值模拟试验获取了不同结构类型粗粒土抗剪强度参数，建立粗粒土结构信息综合参数与抗剪强度指标间的函数关系式，将其代入粗粒土考虑咬合力作用力的抗剪强度公式，建立了嵌入结构信息综合参数的粗粒土强度模型。

3) 通过与试验数据和Mohr-Coulomb准则计算值对比，验证本文提出的嵌入初始结构信息的抗剪强度模型能够较好地适用于低应力下的粗粒土强度特性的表征。