山地履带车辆软坡路面稳态转向模型建立及验证

贾鑫，谢铌，丁小兵，刘良豪，刘妤*

（1.重庆理工大学机械工程学院，重庆 400054；2.重庆鑫源农机股份有限公司，重庆 400039）

山地履带车辆具有接地比压小、转向灵活、越野能力强等优点，广泛应用于丘陵山区农业生产。作为机动性的重要组成部分，履带车辆转向性能引起广泛关注[1-2]。

国内外学者围绕履带车辆转向性能开展了大量研究。程军伟等[3]基于滑转滑移条件讨论了履带车辆平稳转向的过程，建立了虑及履带打滑的转向模型，并通过试验验证了所建模型更符合履带车辆转向实际；史青录等[4]研究了履带车辆斜坡转向时的运动学、动力学和稳定性问题，并分析了瞬时转向中心偏移量的变化规律及影响因素;Solis等[5]基于偏微分方程建立了用于估计土壤动态剪切位移的运动学模型，并通过模拟结果与实车测试结果的对比验证了模型的有效性；Wong等[6]结合剪应力模型分析了履带车辆的转向运动规律；王红岩等[7]建立了高速履带车辆的转向模型，分析了转向过程中运动学和动力学参数的变化规律，并通过对比实车测试结果与模型计算结果验证了转向模型的准确性；Edwin等[8]改进了履带-土壤接触处剪切位移分布的计算方法，建立了履带车辆松软路面环境下的运动模型，并模拟了转向过程。综上，这些研究多数未考虑特殊作业环境对履带车辆转向模型的影响，而且甚少基于理论模型分析履带车辆完整转向过程。

履带车辆转向过程始终伴随着两侧履带的滑移和滑转，考虑履带滑动和离心力的影响，本研究建立了软坡路面环境下履带车辆稳态转向的理论模型，并探讨了坡角、转向半径、转向角度和土壤环境等因素对山地履带车辆软坡地面转向性能的影响，旨在为履带车辆转向系统设计及其软坡路面转向特性分析提供参考模型。

1 材料与方法

1.1 转向模型构建

1.1.1 基本假设为研究山地履带车辆软坡路面转向性能，作如下基本假设：①丘陵地形中，坡度>25°的陡坡地不适宜农业生产，为此，假设山地履带车辆的行驶环境为倾角在(0°,25°]范围内的坡地，并忽略地面不平度的影响[9]；②转向过程中履带底盘的行驶阻力系数保持不变；③不考虑侧向土壤对履带产生的推土阻力；④履带接地段的压力分布呈连续线性分布，不计履带张力变化对接地段压力的影响。

1.1.2 坐标系建立为分析履带车辆坡地行进时的转向特性，分别以转向中心和履带车辆建立定坐标系（xm，ym，zm）和动坐标系（xi，yi，zi）（i=1，2，分别代表内、外侧履带），如图1所示[9-10]。在定坐标系中，O为履带车辆的重心，M为履带车辆的转向中心，α为坡地倾角，履带车辆绕转动中心M进行转向运动。在动坐标系中，坐标原点分别为两侧履带的几何中心Oi（i=1，2），动坐标系的x轴沿车体横向中心线指向车体外侧，y轴沿车体纵向中心线，z轴垂直于底盘平面。同时，由于本文针对的是坡地路面环境，因此，将在定坐标系和动坐标系下描述的坡地转向运动利用3-1-2型欧拉旋转序列的旋转矩阵投影[11]至惯性参考系（xo，yo，zo）。

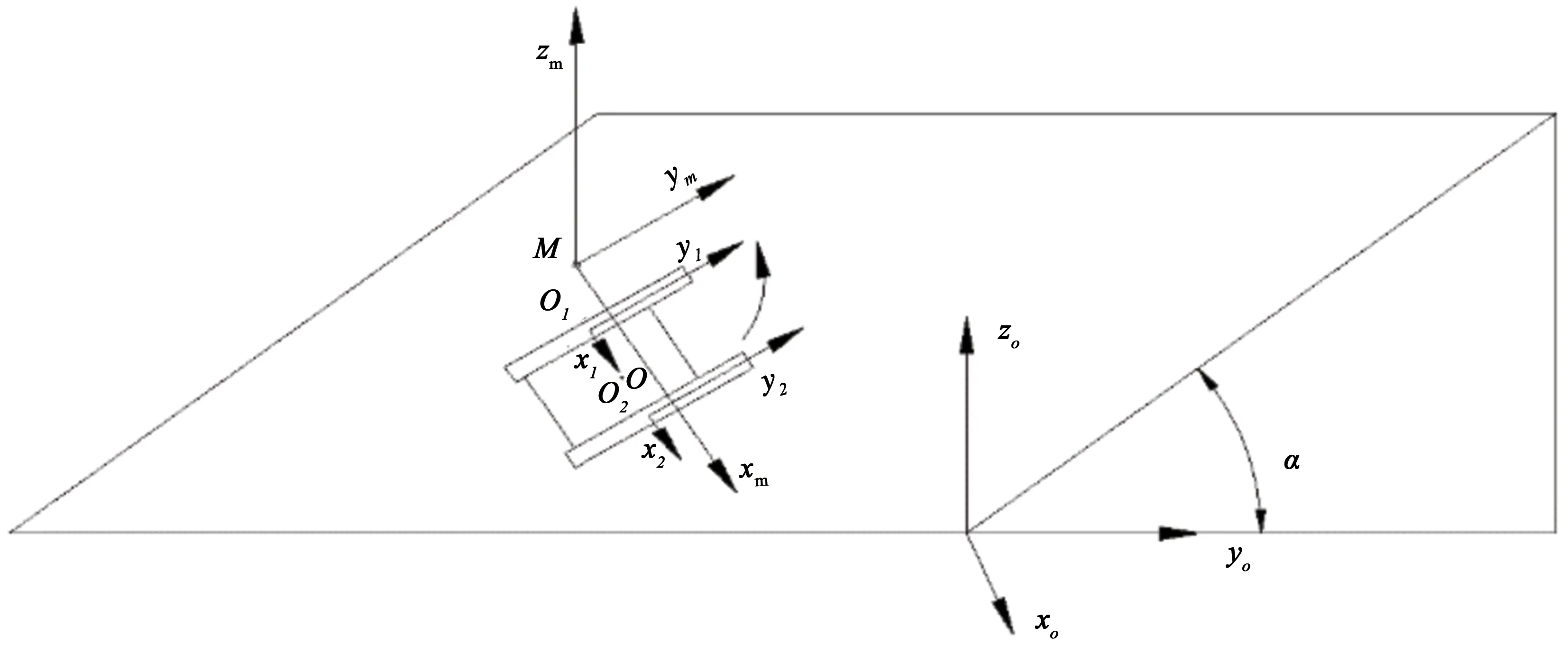
图1 履带底盘坡地转向坐标系Fig.1 Coordinate system for crawler chassis slope steering

1.1.3 坡地转向运动模型履带车辆坡地转向运动模型如图2所示[9,12]。鉴于转向过程中两侧履带的滑移和滑转会导致履带的速度瞬心与各自的几何中心不重合[13]，因此，记A1、A2分别为内、外侧履带速度瞬心O"i（i=1，2）相对于各自几何中心Oi（i=1，2）的横向偏移量，D0为履带车辆重心O相对于转向中心M的纵向偏移量。同时，记cx、cy分别为履带车辆的重心O相对于其几何中心Oz的横向、纵向偏移量。

图2 履带车辆坡地转向运动模型Fig.2 Steering motion model of tracked vehicle on slope road

由于两侧履带在转向过程中存在滑动，只有履带的瞬时转向中心在纵向方向上的速度（v）与履带的理论速度相等[14]，转向速度计算公式如下。

式中，为转向角速度；R为转向半径；β为侧滑角；B为履带车辆的轨距；i=1,2分别对应内、外侧履带，且i=1时取“-”，i=2时取“+”。

由此可分别计算得履带车辆的实际转向半径R和转向角速度。同时，采用滑移率δi作为评价履带车辆的滑移/滑转程度的指标[13]。

1.1.4 坡地转向动力学分析履带车辆转向过程中 的 受 力 如图3所 示[12]。图 中，Gmx、Gmy、Gmz，Fcx、Fcy、Fcz分别为重力G、离心力Fc在动坐标系下的分力；N1、N2，Fx1、Fx2，Fy1、Fy2，MR1、MR2，R1、R2分别为左（1）、右（2）侧履带受到的法向约束力（即支撑力）、横向阻力、牵引力、转向阻力矩和行驶阻力。

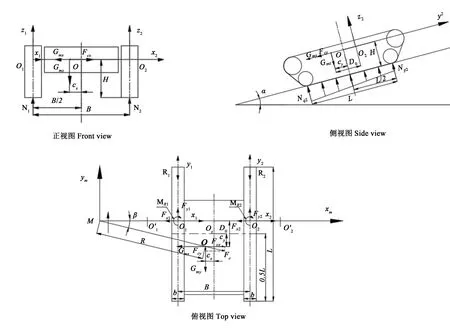
图3 履带车辆坡地转向受力分析Fig.3 Force analysis of tracked vehicles turning on slope road

①支撑力及接地压力。结合图3正视图，通过平衡方程（5）可求得两侧履带所受的支撑力。

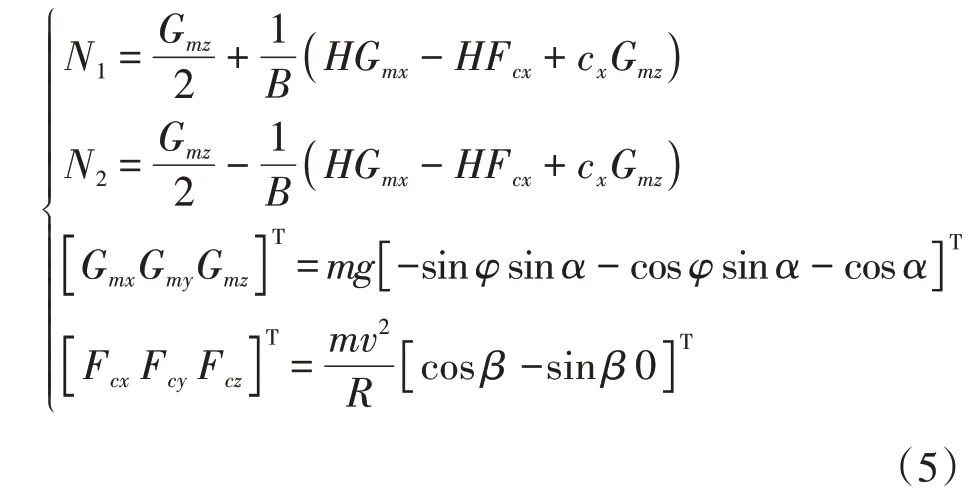
式中，H为履带几何中心到地面的高度，φ为转角。

履带车辆在坡地路面行驶时，接地压力因压力中心偏移而呈梯形分布[15]。记两侧履带的前端（最小）接地压力为Npi（i=1，2），后端（最大）接地压力为Nqi（i=1，2），结合图3侧视图，通过平衡方程可求得内、外侧履带的接地压力及其最大、最小值。

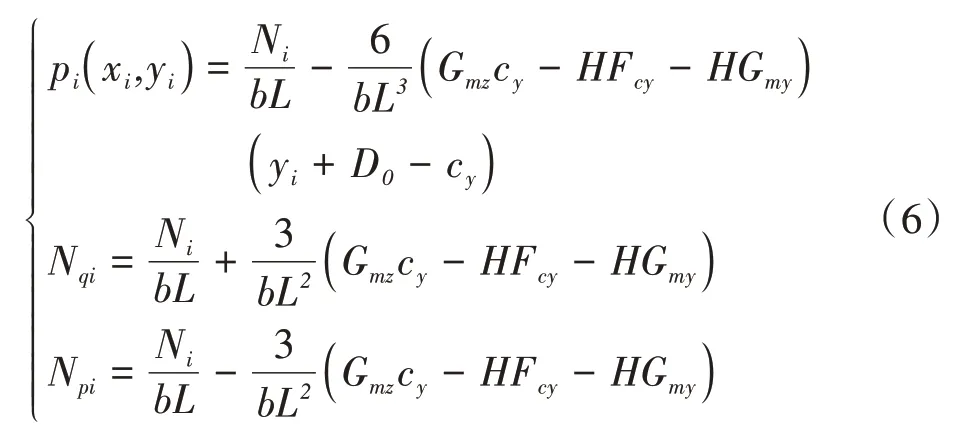
式中，L为履带的长度；b为履带宽度。

②牵引力及横向阻力。履带车辆运动过程中，土壤与履带相互之间会产生剪切力τ。结合Janosi剪切模型[16]，剪切力可表示如下。

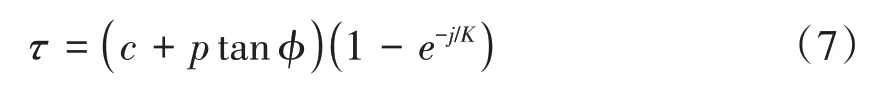
式中，c为土壤的内聚阻力；p为履带上任意一点受到的法向压力；ϕ为包络土壤内摩擦角；K为剪切应力作用下土壤的变形模量；j为剪切变形。

履带接地段上任意一点的速度分析如图4所示，其中，两侧履带接地段中点Oti（i=1，2）的速度与履带中心Oi（i=1，2）一致。通过计算履带接地段任意点的滑动速度，可得到内、外侧履带接地段任意点处的剪切变形ji(xai，yai)如下。

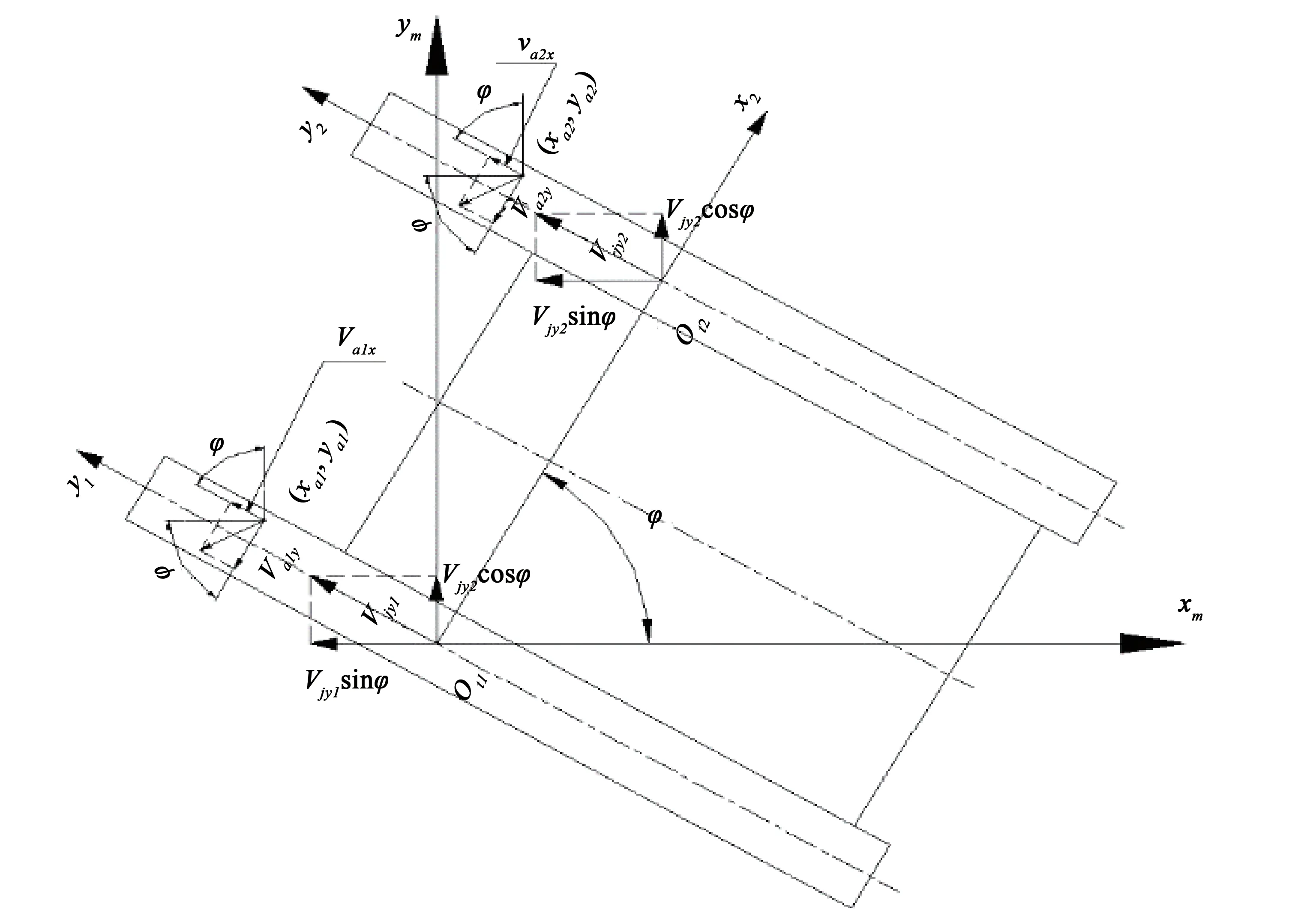
图4 履带车辆速度分析Fig.4 Speed analysis of tracked vehicle

式中，rs为驱动轮半径；wi为内、外侧驱动轮的角速度。

采用网格划分，将内、外侧履带接地段分别划分为m×n个小单元，如图5所示，则履带车辆转向过程中，内、外侧履带与地面剪切力Fi如式（9）所示。同时，结合图4可知，履带车辆行进过程中，履带与地面接触点处的剪切力与履带的滑动速度方向相反。所以，内、外侧履带横向剪切力（即横向阻力）Fxi与纵向剪切力（即牵引力）Fyi计算如式（10）（11）所示。

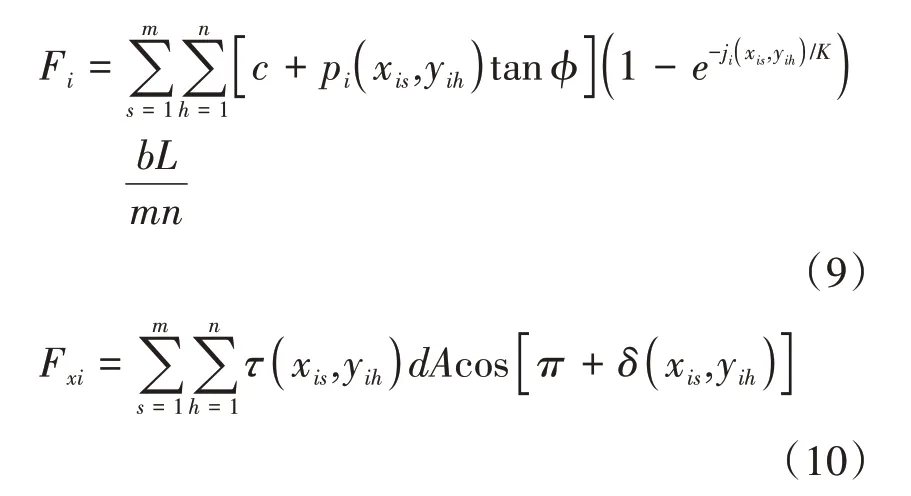
式中，δ(xis,yih)为内、外侧履带任意单元的中心点（xis，yih）的滑动速度与xi轴方向的夹角，且满足以下条件（式12）。

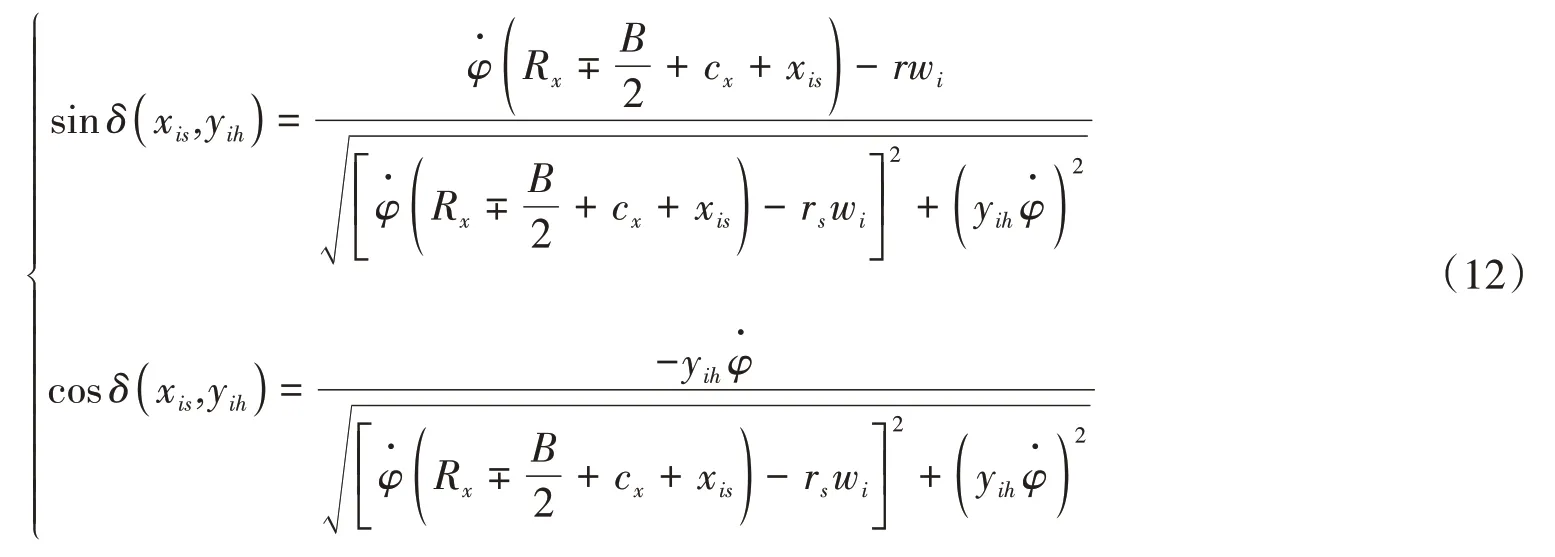
需要说明的是，履带车辆差速转向时，两侧履带牵引力方向可能不一致，当牵引力沿履带自身坐标轴yi（i=1，2）正向时称为牵引力，反之称为制动力。

③转向驱动力矩及阻力矩。转向驱动力矩MTi是每个单元的纵向剪切力对Oz点矩的矢量和，转向阻力矩MRi是每个单元的横向剪切力对履带Oi点矩的矢量和[7]。

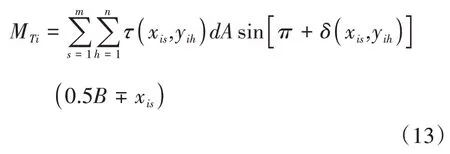
④行驶阻力。行驶阻力可分为外部行驶阻力Roi与内部行驶阻力Rni（i=1，2）。内部阻力（即运行阻力）Rni可根据该侧履带所受到的载荷进行估算[17]。

式中，Ni为对应侧履带所受的支撑力；fg为运行阻力系数，取值范围为0.05～0.08。

当履带底盘行驶速度较慢，可不计风阻，因此，外部行驶阻力主要是沉陷阻力。结合贝克提出的压力-下陷关系公式推导沉陷阻力Rci的计算式[18]如下。

式中，Kc为土壤变形的内聚模量；Kϕ为土壤变形的内摩擦模量；z为土壤的沉陷量；n为土壤变形指数。

因此，行驶阻力Ri计算如下。

1.1.5 动力学模型结合前述分析，建立履带底盘稳态转向的动力学模型。

在车速、履带车辆的结构参数、内外侧履带速度和土壤参数已知的情况下，按照数值迭代计算流程（图6）可以确定方程(18)中的横向偏移量A1、A2和纵向偏移量D03个未知数，进而得到转向过程中偏移量、滑移率等运动学参数，以及牵引力、制动力、转向驱动力矩及阻力矩等动力学参数。同理，可模拟履带车辆坡地转向运动。

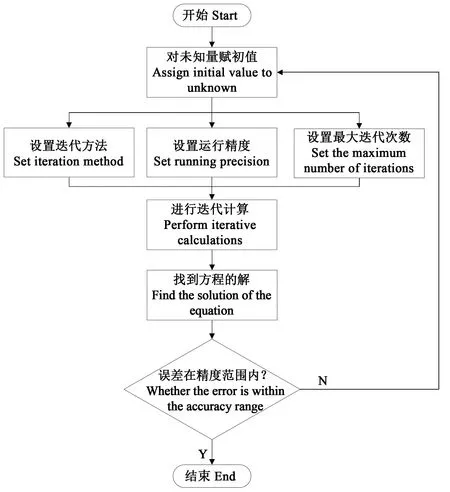
图6 数值迭代法的计算流程Fig.6 Calculation process of numerical iteration method

1.2 模型校验

以自主研制的某小型山地履带底盘为对象，通过对比基于动力学模型的数值分析与基于RecurDyn模型的仿真分析结果[12]，验证前述所建立的履带车辆软坡地面转向模型的有效性。

1.2.1 仿真模型及参数试验用小型山地履带底盘结构如图7所示[9,19]。该履带底盘整体尺寸为1 520 mm×1 000 mm×480 mm，基本结构参数如表1所示。

表1 履带底盘基本参数Table 1 Basic parameter of crawler chassis

图7 小型山地履带底盘结构Fig.7 Structure and simulation model of the small crawler chassis

1.2.2 主要分析条件设置履带机械的转向方式一般选用差速转向[20]。鉴于试验用履带底盘的驱动轮转速在6~12 rad·s-1范围内，因此，左、右侧履带的驱动轮转速设置如图8所示。考虑到山地履带车辆在丘陵山区常见的工作环境为砂壤土，坡度≤10°，设定行驶路面为黏性土，坡地倾角为10°，且假定履带底盘的转向方向为逆时针。

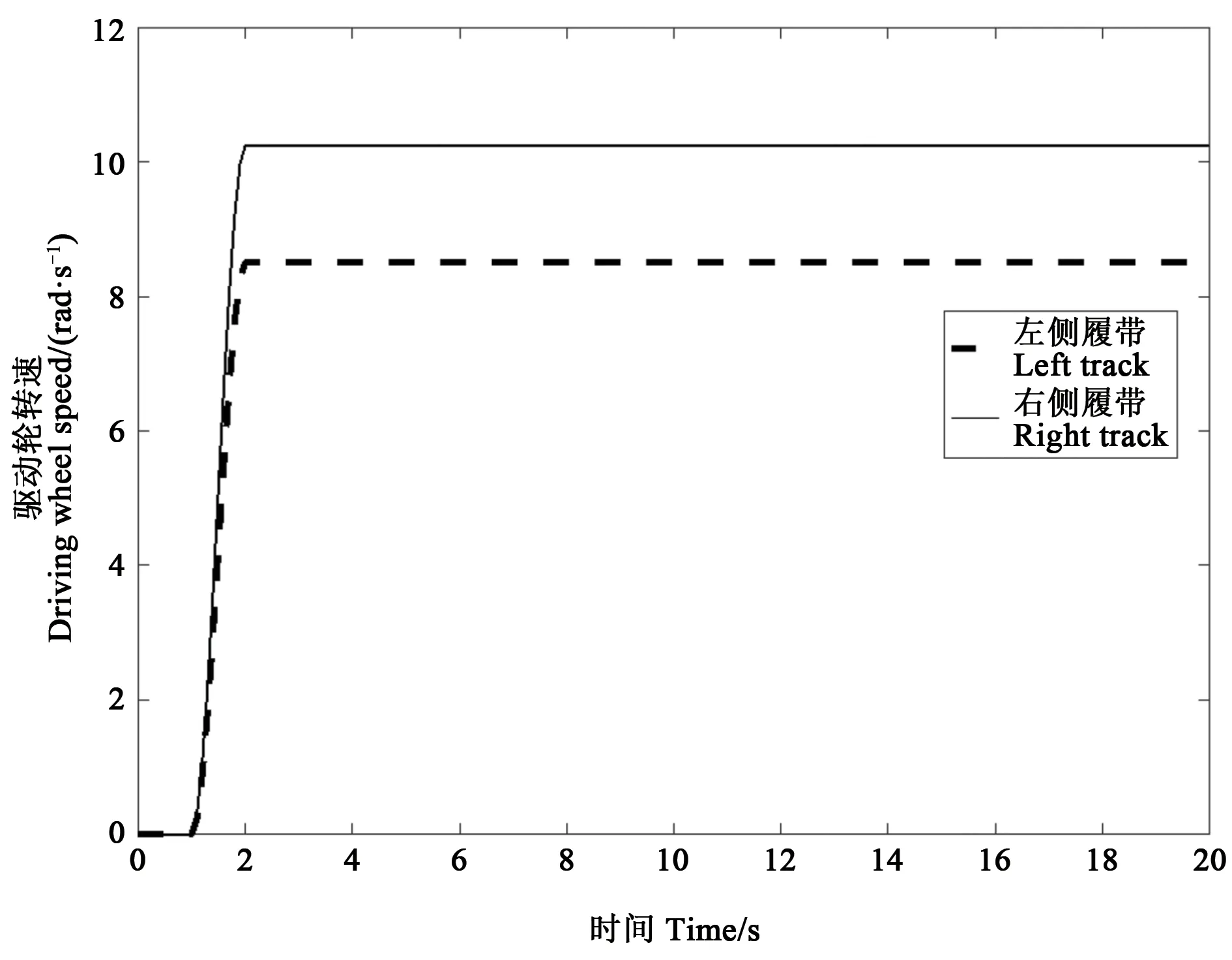
图8 驱动轮转速设定Fig.8 Speed setting of the driving wheel

1.3 坡地转向性能影响因素

影响履带车辆坡地转向性能的主要因素有坡角、转向半径、转向角度和土壤环境等。在分析相关影响时，主要针对10°、15°、20°斜坡角度和黏性土、砂质腐殖土、沙土3种土壤环境[21]，土壤参数设置如表2所示。同时，假设转向半径在1～5 m范围内，转向速度为0.8 m·s-1，并在忽略转向角度变化的情况下分析坡角、转向半径和土壤环境对履带底盘转向性能的影响[22]。

表2 不同土壤基本参数［21］Table 2 Basic parameters of different soils［21］

在转向半径一定的情况下，随着转向角度的变化，牵引力、制动力、转向驱动力矩和阻力矩等参数都会发生规律性变化[23]。因此，假设履带底盘的转向半径为3 m，进一步分析了坡角、转向角度对履带底盘转向性能的影响。

1.4 仿真结果评价

利用决定系数（R2）评估数值分析与仿真分析结果的符合程度[22]。

式中，hi为数值分析结果，si为仿真分析结果，sp为仿真分析结果的平均值。

2 结果与分析

2.1 模型有效性分析

履带底盘的质心位移可以通过其质心位移反映。基于动力学模型的数值分析和基于RecurDyn的仿真分析所得到的履带底盘质心位移结果对比如图9所示。可以看出，两种方法所得到的质心位移具有相同的变化规律；履带底盘的转向运动趋于稳态后，质心位移随时间呈近似正弦的变化规律。进一步分析可得，两种方法所得到的质心在X、Y、Z方向的最大相对误差分别为13.29%、14.69%、9.49%，平均相对误差分别为3.57%、1.23%、2.79%。

图9 质心位移数值分析与仿真分析结果对比Fig.9 Comparison of results of numerical analysis and simulation analysis of centroid displacement

从图10可以看出：10 s左右，履带底盘旋转角度约90°，达到最高点；20 s左右，履带底盘运动到最左侧；同时，由于偏移量的影响，每时刻的转向半径均在发生变化，这导致履带底盘的转向运动轨迹呈现类圆型。质心在X、Y、Z方向位移的决定系数分别为0.999、0.999、0.994。

图10 质心在X和Y方向的位移Fig.10 Displacement of the center of mass at the X&Y direction

上述对比分析结果表明，基于动力学模型的数值分析和基于RecurDyn的仿真分析所得到的履带底盘质心位移具有较好的一致性，误差小于15%，这验证了所建立的履带车辆坡地转向模型的有效性。

2.2 不同因素对转向性能的影响

2.2.1 对滑移率的影响从图11可以看出，同种土壤环境下，δ1和δ2均随α的增加而略有增加，这说明坡角越大，履带车辆转向运动中的滑移率越大，越易发生失稳；δ1和δ2均随R的增大而减少，这说明转向半径越大，履带车辆在转向运动中越不容易产生滑移/滑转；不同土壤环境下，δ1和δ2不同，比较而言，δ1和δ2在砂质腐殖土环境下最高，这说明履带车辆在砂质腐殖土环境下进行坡地转向运动时更易产生滑移。

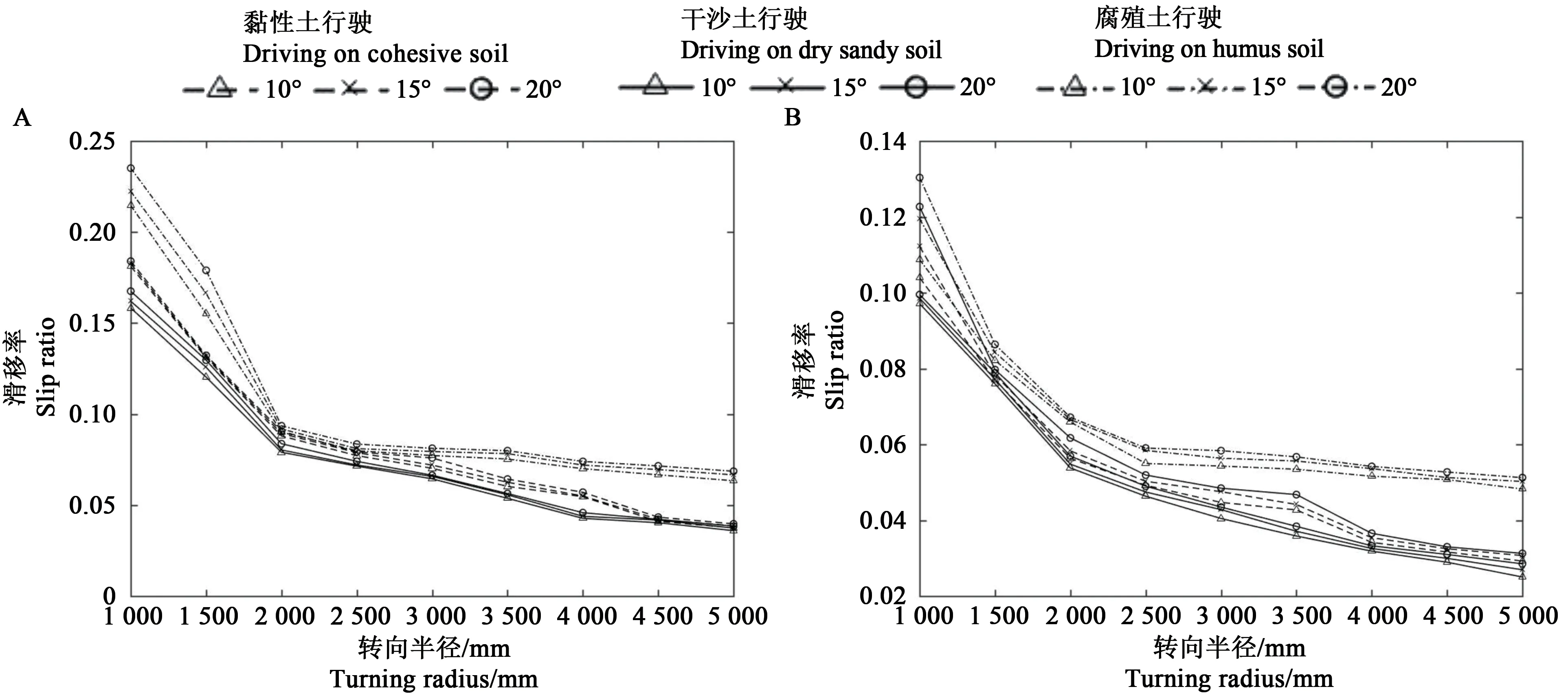
图11 滑移率随坡角、转向半径和土壤环境的变化Fig.11 Change of the slip rate with slope angle，turning radius and soil environment

2.2.2 对制动力和牵引力的影响从图12可以看出，不同土壤环境下，Fy1、Fy2随α和R的变化趋势一致，二者均随α或R的增加而减小。坡角越大，履带车辆越易产生滑动，越难实现转向；在α和R一定的情况下，牵引力大于制动力，这说明牵引力大于制动力才能实现履带车辆的转向运动；不同土壤条件下，牵引力、制动力的数值相差较大，比较而言，在砂质腐殖土环境下的牵引力和制动力是最大的，这说明在砂质腐殖土环境下履带车辆需要更大的动力才能完成坡地转向运动。

图12 牵引力和制动力随坡角、转向半径和土壤环境的变化Fig.12 Change of the traction and braking force with slope angle，turning radius and soil environment

2.2.3 对转向驱动力矩和阻力矩的影响转向驱动力矩MT、阻力矩MR随坡角α、转向半径R和土壤环境的变化情况如图13所示，其中，正值代表力矩方向为逆时针，反之为顺时针。可以看出：不同土壤环境下，MT、MR随α和R的变化趋势一致，二者均随α或R的增大而减小；比较而言，履带车辆在砂质腐殖土环境下的MT、MR最大；在同种土壤环境下，履带车辆的转向驱动力矩和阻力矩受坡角的影响较小，这说明土壤环境对转向驱动力矩和阻力矩的影响比坡角的影响更为显著。

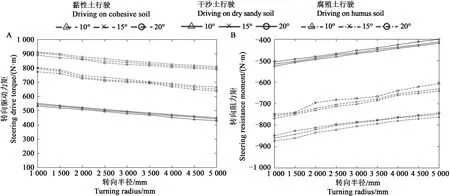
图13 转向驱动力矩和阻力矩随坡角、转向半径和土壤环境的变化Fig.13 Change of the steering drive torque and resistance torque with the slope angle，steering radius and soil environment

2.2.4 对偏移量的影响横向偏移量A1、A2和纵向偏移量D0随坡角α、转向半径R和土壤环境的变化情况如图14所示。可以看出：A1、A2和D0随R的增加而减少，随α的增加而增加；不同土壤环境下，A1、A2不同，比较而言，A1、A2在砂质腐殖土环境下最大；相比A1、A2的变化而言，D0受土壤环境和坡角的影响较小。

图14 偏移量随坡角、转向半径和土壤环境的变化Fig.14 Change of the offset with slope angle，turning radius and soil environment

2.3 坡角和转向角度对转向性能的影响

2.3.1 对滑移率的影响从图15可以看出，δ1和δ2随φ的变化呈现相反的变化趋势。当φ为0°、180°、360°时，内、外侧履带的滑移率差值最大，这些时刻点履带车辆转向时最容易发生滑移；在φ一定的情况下，随着α的增加，δ1和δ2均增加，这说明坡角增大会增加履带车辆坡地转向发生滑移的可能性。

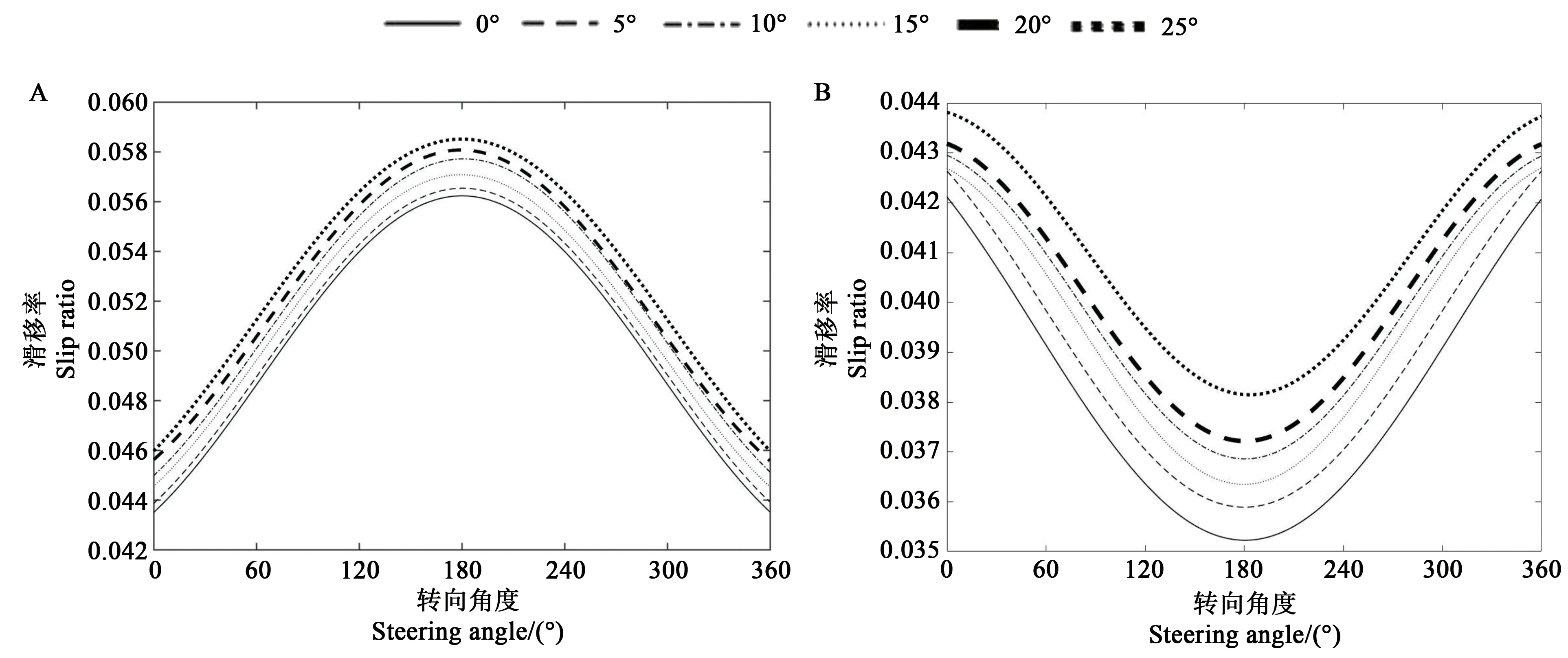
图15 滑移率随坡角和转向角度的变化Fig.15 Change of the slip rate with slope angle and steering angle

2.3.2 对制动力和牵引力的影响从图16可以看出，α越大，Fy1、Fy2的变化幅度越大；Fy1、Fy2随φ的变化呈现周期性变化。当φ=90°时，Fy1、Fy2都达到最大值；当φ=270°时，Fy1、Fy2都达到最小值；当φ∈[0,90°)∪[270°,360°)时，履带车辆处于上坡转向阶段，Fy2增加，Fy1也会增加，这说明在上坡阶段需要更多的动力，而当φ∈[90,270°)时，履带底盘处于下坡转向阶段，Fy1、Fy2均会减小，此时重力在履带坐标系的分力对转向起到了推动作用。

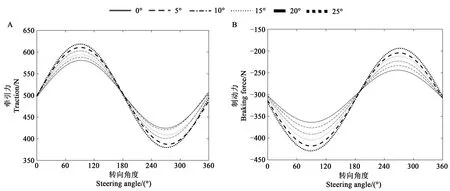
图16 牵引力、制动力随坡角和转向角度的变化Fig.16 Change of the traction and braking force with slope angle and steering angle

2.3.3 对转向驱动力矩和阻力的影响从图17可以看出，MT、MR均随α增大而所增加，这说明履带车辆坡地转向时，α越大，完成转向运动所需要提供的动力越多；MT、MR均随φ的变化呈现周期性变化。当φ=90°时，MT、MR都达到最大值，此时履带车辆转向运动所需要的动力最大。

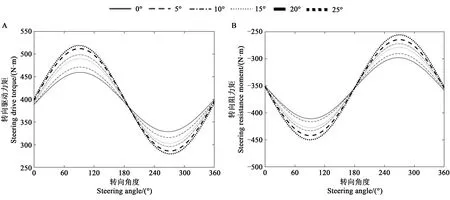
图17 转向驱动力矩、阻力矩随坡角和转向角度的变化Fig.17 Change of steering drive torque and resistance torque with slope angle and steering angle

2.3.4 对偏移量的影响横向偏移量A1、A2和纵向偏移量D0随坡角α和转向角度φ的变化情况如图18所示。可以看出，A1、A2随φ的变化呈现相反的变化趋势。同时，D0随φ呈正弦变化，当φ为90°或270°时，D0的绝对值达到最大，说明此时履带车辆离转向中心最远，需注意运动范围，避免意外发生；在φ一定情况下，随着α的增加，A1、A2都略有增加，但D0发生明显变化，在α=25°时，履带底盘相对转向中心的最大纵向偏移量可达0.3 m以上，这种情况下履带底盘更容易发生侧滑甚至倾翻现象，同时，过大的纵向偏移量也会严重影响履带车辆的稳定性和可控性。

图18 偏移量随坡角和转向角度的变化Fig.18 Change of the offset with the slope angle and steering anglev

3 讨论

考虑丘陵山区特殊作业环境对履带车辆转向模型的影响，通过理论分析及推导，得到了牵引力、制动力、转向驱动力矩和阻力矩等关键参数的解析式。可用于不同履带底盘在不同作业环境下的转向运动分析，也可用于履带底盘的优化设计。

考虑履带滑动和离心力的影响，建立了软坡路面环境25°坡角范围内履带车辆稳态转向理论模型，并结合自主研制的小型山地履带底盘，通过对比基于理论模型的数值分析与基于RecurDyn模型的仿真分析结果，验证了转向模型的有效性。依托该模型，可以更方便地评估履带底盘在不同软坡路面环境下的转向性能，大大降低实车试验工作量，提高试验效率。

结合试验用小型山地履带底盘，分析了坡角、转向半径、转向角度和土壤环境等主要因素对履带底盘坡地转向性能的影响。结果表明：偏移量和滑移率随坡角及转向半径的变化趋势相反；牵引力、制动力、转向驱动力矩和阻力矩等参数随坡角及转向半径的变化趋势一致，随转向角度在[0,360°)内变化而呈现周期性变化；履带车辆在转向半径越大、坡角越平缓的情况下越易于实现转向运动，土壤环境是影响履带车辆转向特性的显著因素。

本研究可为履带车辆转向系统设计及其软坡路面转向特性分析提供参考模型。