基于离散元法的水田刀片抛浆运动分析与试验

陈重成, 任金波, 万家明, 郑书河

(福建农林大学机电工程学院，福建 福州 350108)

制浆机为南方地区水稻育秧使用的水田边界制浆机械[1-3]，其操作方式简单、工作效率高，能大量减轻水稻育秧制浆过程中的人工劳动强度.制浆机在作业过程中通过水田刀片的旋转运动以及整机的前进运动将水田泥浆抛至一侧的育秧盘内.水田刀片作为水田制浆机的关键部件，其结构和形状对抛浆运动起着至关重要的作用.因此研究水田刀片的结构对抛浆运动的影响是进一步优化设计刀片和分析泥浆运动状态的基础.目前，国内外学者针对刀片和土壤的相互作用关系以及抛土抛浆行为展开大量研究.熊平原等[4-5]通过研究传统的旋耕刀在作业过程中的运动曲线与受力，分析了旋耕刀结构参数与旋耕三向受力关系.秦宽[6]在传统的旋耕刀刀背处增加了一把抛土片并与旋耕刀组合使用，验证了增加抛土片后的抛土刀有更好的抛土效果.丁为民等[7]研究了传统旋耕刀正反转与功耗的关系，发现反转能够获得更高效率.谢宇等[8-11]改进并优化了水田制浆机的刀片的结构，使水田刀片能够获得更高的作业效率.臧家俊等[12]研究了果园覆土机的覆土原理，通过覆土轮抛土分析抛土厚度与抛土的均匀性.吴明亮等[13]分析了旋耕设备在作业过程中土壤颗粒抛出过程中的理论状态.杨薇等[14]使用离散元法分析开沟器排土过程.而对水田刀片的抛浆研究报道较缺乏.本研究通过数值模拟和试验设计研究新型水田刀片工作参数对抛浆性能的影响，对刀片相关参数进行了优化[15-16]，为后续水田刀片的研究和育秧制浆机的研发提供依据.

1 刀片溅泥过程

1.1 水田刀片结构

本研究的刀片是一种以旋耕刀为基础改进的新型水田刀片，刀片结构如图1所示.刀片侧切刃为破土能力较好的阿基米德曲线[17].溅泥板形状为混合部分直线的半椭圆形，并通过焊接的方式固定于正切面刀背处.工作时，水田刀片通过侧切刃旋耕破土并利用溅泥板将泥浆抛出，从而达到将泥浆抛至育秧盘中的目的.

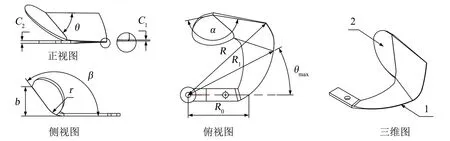
1.刀片侧切刃；2.溅泥板；θ为正切刃与溅泥板夹角(°)；α为正切面与溅泥板的夹角(°)；R0为侧切刃起始半径(mm)；R1为侧切刃终点半径(mm)；R为刀辊回转半径(mm)；θmax为侧切刃包角(°)；C1为刃口厚度(mm)；C2为刀柄厚度(mm)；b为工作幅宽(mm)；r为弯折半径(mm)；β为正切面弯折角(°).图1 水田刀片结构Fig.1 Structure of pulping blade

1.2 抛浆过程

为分析刀片作业过程中泥浆受力情况与抛出后泥浆的运动情况.以刀片弯折点为原点，以刀片旋转轴方向为x轴，以刀片侧切刃方向为y轴建立xoy坐标系，分析泥浆随同刀片转动即将抛出过程中的受力情况(图2a).将刀片正切面与侧切面简化为垂直于xoy平面的两平面，并假设泥浆颗粒由混合了部分水分的固体土壤颗粒构成，同时不考虑颗粒间的相互碰撞作用.该过程中泥浆受力有正切面支撑力Fn、泥浆转动过程离心力Fl、泥浆与正切面之间的摩檫力和粘性力Ff，泥浆颗粒重力在xoy平面投影极小，因此这些力忽略不计.泥浆受离心力与支撑力合力Fa克服摩擦力与粘性力后固体颗粒所受合力沿正切面向下，在合力作用下颗粒在正切面上滑动，最终滑出正切面时抛出.泥浆抛出时刻的速度为：

(1)

式中:νx为泥浆颗粒抛出时刻沿x方向的速度(m·s-1)；νy为泥浆颗粒抛出时刻沿y方向的速度(m·s-1)；ν0为泥浆运动初始速度(m·s-1)；μ为动摩擦因数；ma为固体颗粒的质量(kg)；b为刀片工作幅宽(m)；β为刀片弯折角(°).

泥浆离开刀片后只受重力作用，颗粒运动轨迹可简化为一条抛物线. 运动过程与旋耕刀抛土过程相似[6]，如图2b所示.侧向抛浆距离为：

(2)

(3)

νz=Rωsinδ2

(4)

式中:B为侧向抛土距离，m；δ为抛出时刻速度与地面夹角，°；δ1为速度在地面的投影与y方向的夹角，°；δ2为刀片瞬时速度与地面的夹角，°；νw为刀片旋转运动瞬时速度，m·s-1；R为刀片回转半径，m；ω为刀片角速度，r·min-1.

2 虚拟仿真试验与台架试验

2.1 试验设计

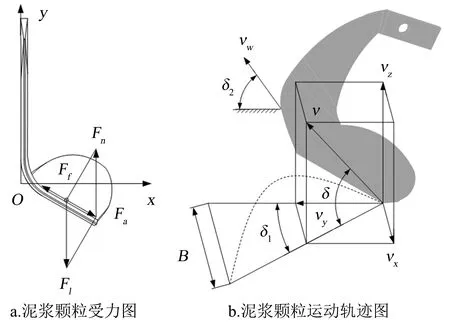
图2 泥浆运动分析图Fig.2 Motion diagram of mud movement

由建立的水田刀片抛浆过程的理论模型可知，影响泥浆抛出距离与抛出质量的工作参数主要有旋转速度ω、刀具工作幅宽b、刀具回转半径R、刀具作业高度h.通过单因素试验发现刀具工作幅宽、作业高度与旋转速度对抛浆距离与抛浆质量的影响显著，且经过单因素试验进一步发现刀具工作幅宽、作业高度与旋转速度分别为35～55 mm、0～50 mm、191.0～286.5 r·min-1时刀片作业具有较好的抛出性能与抛出质量.因此，选择刀具工作幅宽b、刀具作业高度h与刀具旋转速度ω为因素，并分别设为X1、X2、X3布置三水平，进行Box-Behnken(BBD) 中心组合方法正交实验.同时选择刀片作业的抛浆距离与抛浆质量作为衡量刀片作业性能指标.因素设置水平表如表1所示.

表1 因素水平表Table 1 Levels of different factors

仿真试验：模拟刀片实际作业过程，在1 500 mm×1 500 mm×1 500 mm的封闭泥浆池中完成.如图3所示，l1为390 mm，l2为200 mm.将刀片缓慢插入泥浆中，然后刀片以设定转速旋转的同时以500 mm·s-1的速度前进，刀片工作时间设定为2 s.工作结束后，刀片抛出的泥浆落入右侧接收盘，将右侧接收盘根据距离不同等距划分3个单元格；通过测量不同单元格泥浆质量并根据单元格之间的距离，使用加权平均法得到抛浆距离L，抛浆质量M则为3个接收盘中泥浆质量的总和.

(5)

M=M1+M2+M3

(6)

式中，M1、M2、M3分别为单元格中泥浆质量.

2.2 模型建立

采用EDEM2020软件对水田刀片溅泥的离散元模型进行仿真试验.水稻育秧所需泥浆随水稻品种与地区的不同有所差异.本研究选用福建省福州市闽侯县福建农林大学水稻试验田泥浆作为泥浆参数参考展开仿真试验.在仿真软件中生成土壤颗粒和水颗粒两种颗粒，并充分混合，模拟泥浆.为使仿真试验尽可能顺利，本研究结合EDEM的特点对颗粒模型进行了适当放大，这对仿真结果影响不大[4].土壤颗粒直径选取10 mm，水颗粒直径选取8 mm.为使颗粒混合均匀以模拟泥浆，选择随机生成颗粒的方式，泥浆池为1 500 mm×500 mm×300 mm.

泥浆颗粒泊松比选用0.25，剪切模量为1.24×106MPa ，密度为2 650 kg·m-3.水颗粒泊松比0.5，剪切模量为108，密度103 kg·m-3.试验对象之间的接触参数见表2.考虑到泥浆运动的粘滞作用，本研究选取EDEM的Hertz-Mindlin with JKR模型为颗粒间的接触模型.该模型通过颗粒之间的内聚力计算模拟颗粒间的粘滞作用.

刀片通过Solidworks建模，并使用一种旋耕刀刀座，以4个为一组均匀分布装配后插入EDEM软件中.材料选择65Mn，正切刃与溅泥板夹角θ为45°，刀刃厚度C1为2 mm，刀背厚度C2为5 mm，正切面与溅泥板倾斜角α为110°，正切面弯折角β为120°，正切面弯折半径r为30 mm，侧切刃起始半径R0为125 mm，侧切刃终点半径R1为218 mm，刀辊回转半径R为225 mm，侧切刃包角θmax为27°.

仿真试验时间步设定为1.66×10-6s，每0.05 s

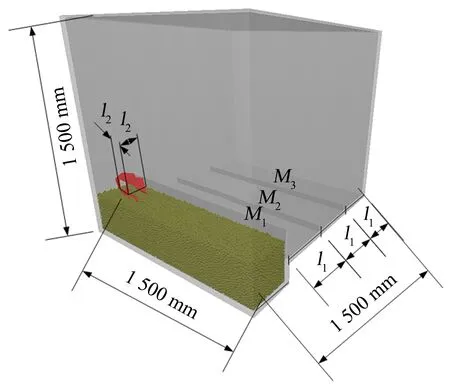
图3 EDEM仿真试验过程Fig.3 EDEM simulation test

表2 接触参数Table 2 Parameters for different contact types

记录一次数据，每次共记录40组数据点，试验结束后分别统计三单元格内泥浆质量计算抛浆距离与抛浆质量.

2.3 台架试验设计

1.变频调速器；2.减速电机；3.转速传感器；4.水田刀片；5.齿轮齿条滑台导轨；6.分格收集盘；7.电子称重系统.图4 台架试验Fig.4 Bench test

台架试验地点选择在福建农林大学机电工程学院，选择试验序号为4、8、14、16以及最优组合5组参数进行试验.试验装置主要有异步电机YL90S-2(上海韩奥电机有限公司提供)、CBX1204-1000减速电机、齿轮齿条滑台导轨、水田刀片，变频调速器、分格收集盘、电子称重系统(深圳使索沃数码有限公司提供)、转速传感器.试验水田土壤选用福建农林大学旗山校区水稻试验田，土壤含水率约为49%.为了剔除试验过程中某些参数的影响以及水田土壤不均匀导致的误差，将试验土壤均匀搅拌；同时将泥浆池固定，调节电机的高度以控制刀片高度.每组试验分2次进行，首次试验不测量数据，通过变频调速器与转速传感器控制刀片转速稳定于目标值，第2次试验得到稳定转速下的试验结果. 台架试验如图4所示.

3 结果与分析

3.1 仿真试验

水田刀片在不同工作幅宽X1、刀片高度X2、旋转速度X3下的抛浆质量Mz与抛浆距离L如表3所示.利用Design-Expert13数据分析软件对正交试验结果进行分析，分别对抛浆距离与抛浆质量建立二次回归模型.

3.2 回归分析

3.2.1 抛浆质量 建立工作幅宽X1、刀片高度X2、旋转速度X3与抛浆质量Mz之间的多元二次回归方程，如式(7)所示.

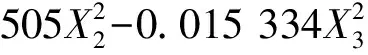
(7)

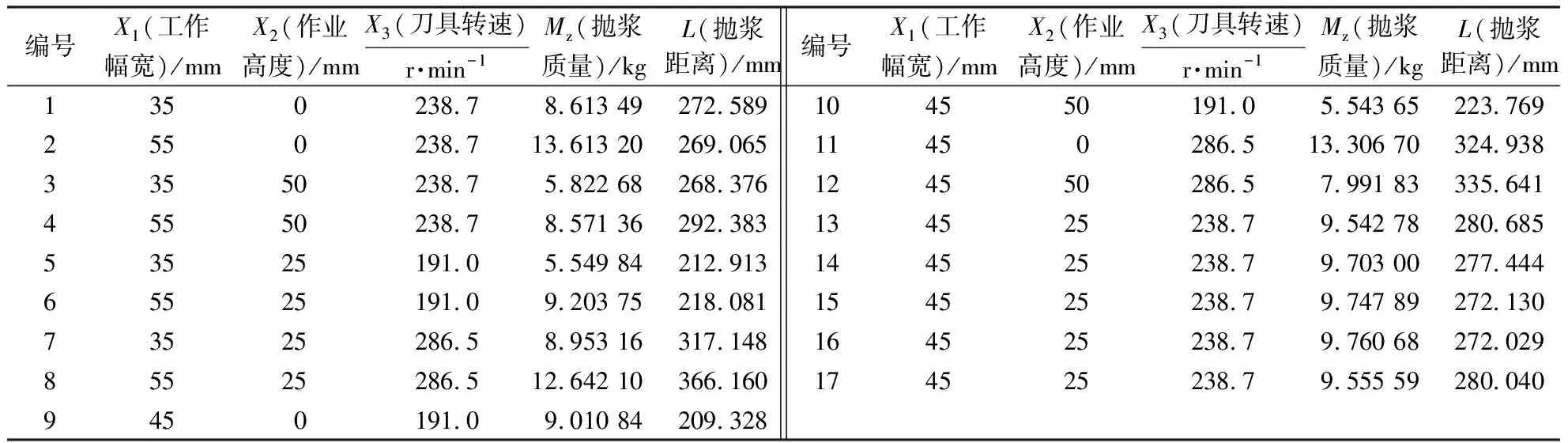
表3 正交试验结果Table 3 Results of orthogonal test

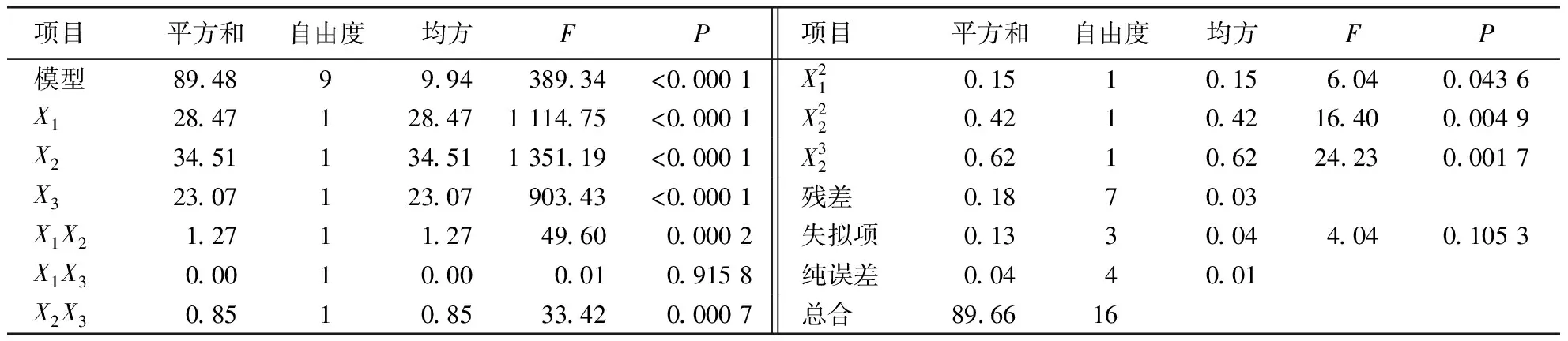
表4 抛浆质量方差分析Table 4 Variance analysis on mass of thrown pulp

3.2.2 抛浆距离 使用逐步回归分析法建立工作幅宽X1、作业高度X2、旋转速度X3与抛浆距离L之间的多元二次回归方程，如式(8)所示.

L=201.568 5-5.235 6X1-0.830 801X2+2.316 72X3+0.027 531X1·X2+0.219 224X1·X3-0.007 474X2·X3

(8)

由表5可知，抛浆距离L的回归模型显著，失拟项不显著，模型P值小于0.001，说明二次拟合情况良好，模型有意义.刀片幅宽X1、旋转速度X3、以及两者的交叉项X1X3的P值均小于0.001表明其对抛浆距离为显著影响.作业高度X2、工作幅宽与作业高度的交叉项X1X2的P值小于0.05，因此其对抛浆距离影响较显著；作业高度与旋转速度的交叉项的X2X3的P值小于0.05，其与抛浆距离关系不显著.

表5 抛浆距离方差分析Table 5 Variance analysis on distance of thrown pulp

3.3 交互因素对抛浆质量与抛浆距离的影响

从图5可知交互因素作用对抛浆质量与抛浆距离的影响.在1个因素为0水平的情况下，其余两因素对试验目标的三维响应曲面图如图5所示.图5a、5d分别为工作幅宽与作业高度对试验结果的影响.从图5可以看出，增加工作幅宽与降低作业高度都会导致抛浆质量显著提高，而对抛浆距离的影响并不明显.图5b、5e分别为工作幅宽与旋转速度对试验结果的影响，从图5可见增加工作幅宽与旋转速度都会导致抛浆质量显著提高，增加旋转速度导致抛浆距离明显增大，而调整工作幅宽对抛浆质量的影响仍不明显.图5c、5f为作业高度与旋转速度对试验结果的影响，从图5可见减小作业高度、增加旋转速度会导致抛浆质量显著提高，增加旋转速度会导致抛浆距离显著增大，而调整作业高度对抛浆距离的影响不明显.

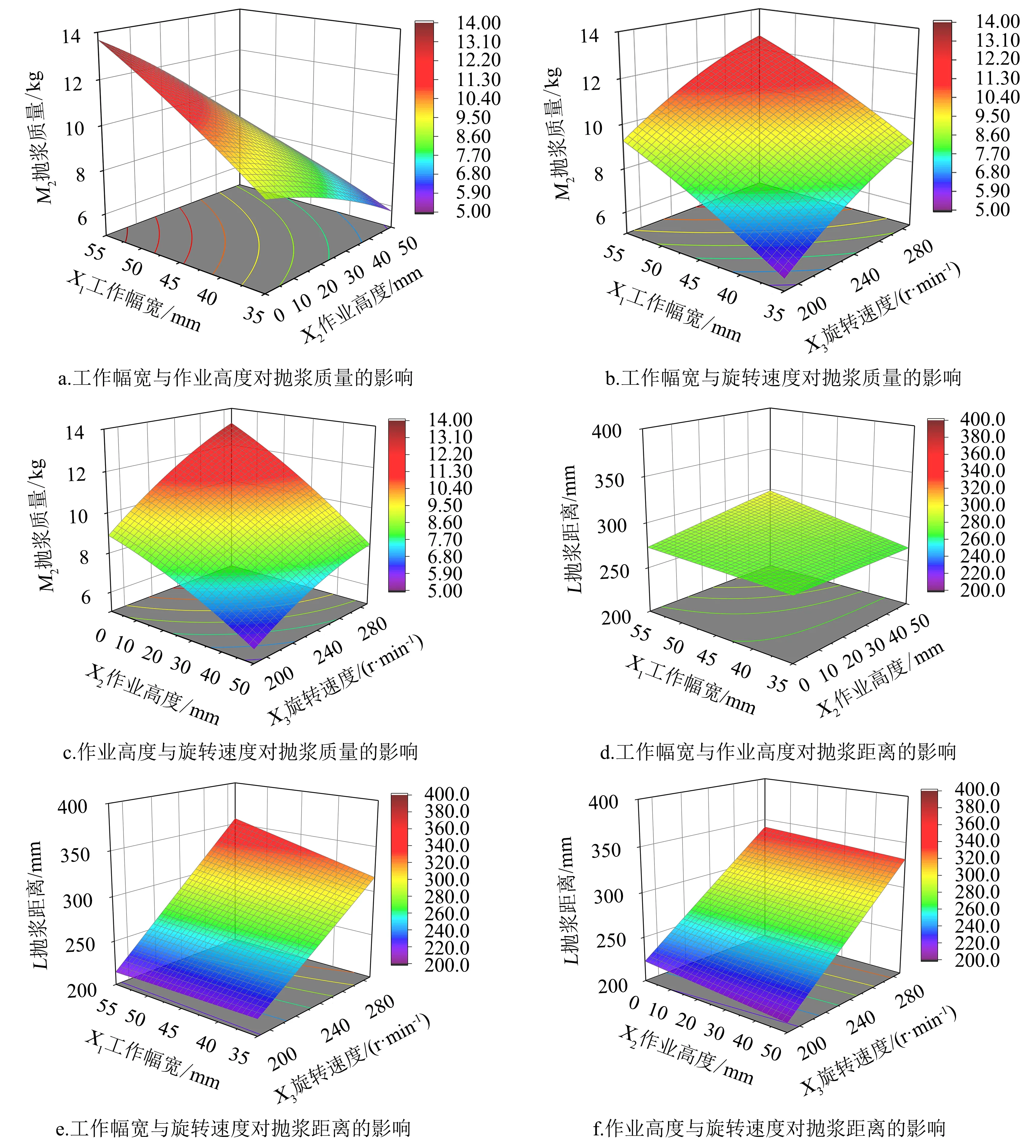
图5 各因素对试验结果响应曲面图Fig.5 Response surface analysis on effect of various factors on pulping distance and pulping quality

3.4 参数优化

通过双目标二次回归方程计算最优工作参数，抛浆距离根据水稻种植田间距离设定为200～300mm时最优，利用Design-Expert分析软件进行双目标参数优化，得到最优参数组合：工作幅宽54.03mm，刀片高度0.212mm，旋转速度242.199r·min-1.最优参数下的抛浆质量为13.618kg，抛浆距离为277.97mm.对于精度要求较高的相似工况可以以此作为参考.考虑到水田刀片工程实际应用过程中对刀片的物理参数无法实现精确控制，将工作参数圆整为工作幅宽55mm，刀具高度0mm，旋转速度238.7r·min-1.在此参数下的试验结果为抛浆质量13.613 2kg，抛浆距离269.065mm.两者差别较小，因此在实际工况下对工作参数进行一定程度的圆整不会影响作业结果，实际工程中可将圆整后的工作参数作为最优组合.

3.5 台架试验

从表6可以看出，抛浆的最大质量出现在最优试验中，其值为12.399kg； 最小质量出现在第4号试验中，其值为8.215kg.5次试验的平均抛浆质量为10.104 2kg，抛浆质量与仿真试验的相对误差为8.95%.抛浆的最大距离出现在8号试验中，其值为354.22mm；最小距离出现在最优试验中，其值为241.56mm.5次试验的平均抛浆距离的相对误差为5.28%，抛浆距离与仿真试验的相对误差为13.10%.

结果表明在误差允许范围内仿真试验能够真实模拟泥浆在水田刀片作用下的抛掷运动.

表6 台架试验结果Table 6 Results of bench test

4 结论

本研究通过分析水田刀片作业过程中受力与运动情况建立相关模型；利用EDEM离散元仿真分析相关参数与抛浆性能之间的关系，并对试验结果进行回归分析，得到结论如下：Box-Benhnken中心组合试验结果表明刀片工作幅宽、刀具作业高度、旋转速度对抛浆质量均有极显著影响，其中刀具作业高度与抛浆质量呈负相关，其余均呈正相关.刀片工作幅宽与旋转速度对抛浆距离有极显著影响，而刀具高度对抛浆距离影响显著，并且三因素与抛浆距离均呈正相关；最优工作参数：水田刀片工作幅宽54.03mm，刀片高度0.212mm，旋转速度242.199r·min-1.最优参数下的抛浆质量为13.618kg，抛浆距离为277.97mm，此时台架试验抛浆质量为12.399kg，误差为8.95%；抛浆距离为241.56mm，误差为13.10%.

台架试验与仿真试验的抛浆质量平均误差为9.48%，抛浆距离为8.46%，说明可以使用离散元仿真法模拟水田刀片抛浆过程，同时使用对质量加权平均的方式计算抛浆距离具有可行性.