时间尺度上相空间中变质量非完整系统的Noether对称性

方 蕊，朱建青

（苏州科技大学 数学科学学院，江苏 苏州 215009）

时间尺度理论是研究离散和连续系统的一种新方法，将离散与连续系统统一起来进行研究。时间尺度理论已经在许多领域中取得了诸多研究成果[1-7]。在力学系统中主要有三种对称性：Noether对称性、Lie对称性以及Mei对称性。对称性理论有许多的用途，其中一种就是用来寻求守恒量，目前已经取得了一系列的研究成果[8-13]。2018年，田雪等人研究了Herglotz型Hamilton系统在时间尺度上的的Noether理论[14]；2020年，张毅研究了完整非保守系统在时间尺度上的Noether定理，并给出了当非保守力不存在时，所对应的Noether等式与守恒量[15]；宋传静、祖启航等人也对时间尺度上的对称性理论进行了研究[16-17]。

在自然界以及工程技术中存在着许多的变质量物体，如：喷气式飞机、火箭、在大气中下落的陨石等。变质量系统主要研究了质量变化的运动物体与其所受力之间的关系。随着科技的不断发展，许多学者对变质量系统的对称性理论进行了研究，并通过对称性来寻求守恒量。1999年，梅凤翔对变质量系统的对称性与守恒量进行了研究[18]；2012年，雷惠方在相空间中对变质量非完整系统的对称性进行了研究，并得到了对称性分别对应的守恒量[19]。关于时间尺度上变质量系统的对称性的研究也取得了一些成果：2019年，吴艳研究了变质量系统在时间尺度上的对称性理论[20]；2020年，阙朝月等人研究了变质量非完整系统在时间尺度上的Lie对称性及其相应的守恒量[21]。在时间尺度上研究变质量系统的对称性是对于经典离散和连续变质量系统的对称性理论的统一与推广。笔者在时间尺度上对于相空间中变质量非完整系统和相应变质量完整系统的Noether对称性进行了研究，得到系统的Noether广义准对称性的判据和Noether守恒量，并给出算例说明结果的应用。

1 时间尺度上相空间中变质量非完整系统的运动方程

设力学系统位形由n个广义坐标qs（s=1，2，…，n）确定，第i个质点在t时刻的质量表示为mi（i=1，2，…，N），△mi表示t+△t时刻质点分离时的微粒质量，设质点的质量为

系统运动受非Chetaev型非完整约束

非完整约束（2）加在虚位移上的限制条件为

这里及文中采用Einstein求和约定。

时间尺度上Lagrange函数为

则时间尺度上变质量非完整系统的微分方程可表示为

其中Ps为广义反推力

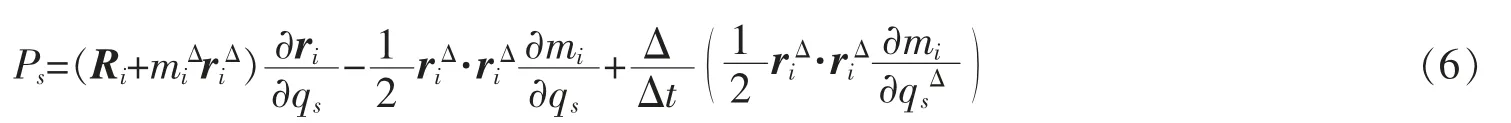
其中ri是第i个质点的矢径，ri△是第i个质点的速度，且

ui是微粒与质点的相对速度。Qs″=Qs″（t，qσ，q△）为非势广义力，λβ是约束乘子。设系统非奇异，即

则方程（5）可表示为

其中

引进广义动量以及Hamilton函数

在正则变量p、qσ下，式（2）、（3）和（10）分别变为

时间尺度上的Hamilton作用量为

时间尺度上相空间中变质量系统的Hamilton原理为

由式（14）、（15）及（17），可得

在式（12）两边对ps求偏导数，可得

根据式（20）、（21）和Dubois-Reymond引理，可得

对式（22）求△导数，可得

方程（21）和（23）称为时间尺度上相空间中变质量非完整系统的运动方程。

由式（15），方程（21）和（23）可进一步表示为

2 时间尺度上相空间中变质量非完整系统的Noether对称性与守恒量

引入无限小变换群

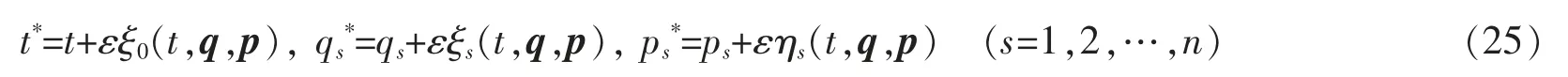
其中ε是无限小参数，ξ0、ξs和ηs是生成元。

定义1如果作用量（16）在无限小变换（25）下，对任意区间[ta，tb]⊆[t1，t2]下式

始终成立，则变换（25）称为Noether广义准对称变换。这里的G（t，qsσ，ps）为规范函数，为全变分。

判据1若存在规范函数G（t，qsσ，ps）使得生成元ξ0、ξs和ηs满足广义Noether等式

其中

则相应对称性为时间尺度上相空间中相应变质量完整系统的Noether广义准对称性。

判据2若存在规范函数G（t，qsσ，ps）使得生成元ξ0、ξs和ηs满足式（27）和限制方程

则相应对称性为时间尺度上相空间中变质量非完整系统的Noether广义准对称性。

定理1对于时间尺度上相空间中相应变质量完整系统，若生成元ξ0、ξs和ηs满足式（27），则该系统的Noether守恒量为

对于时间尺度上相空间中变质量非完整系统，若无限小变换（25）的生成元ξ0、ξs和ηs满足广义Noether等式（27）和限制方程（29），则式（30）同样是该系统的Noether守恒量。

证明

则定理1得证。

推论1若T=R，非完整约束为Chetaev型，由式（27）得到经典相空间中变质量非完整系统的广义Noether等式为

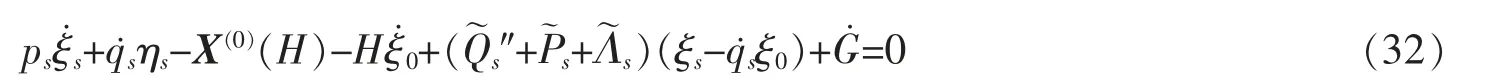
相应经典的Noether守恒量为[21]

3 算例

设时间尺度

一变质量质点，质量为

其中m0和α为常数，且α＞0。

系统的Lagrange函数为

非势广义力不存在，并且微粒的绝对速度为零，即

所受的非完整约束为

假设方程（38）为非Chetaev型，虚位移限制方程为

由时间尺度（34），设t=2m+1∈T，则此时前跳算子为

由此可得步差函数为

根据题意可知

根据式（11）和（12），可得

将Hamilton函数代入式（23），则有

由式（38）、（43和（44），可得

于是有

根据式（27）和（39），可得

对式（47）进行求解

则式（49）为时间尺度上相空间中相应变质量完整系统的广义准对称变换，显然在式（49）下式（48）同样成立，因此，式（49）也为时间尺度上相空间中变质量非完整系统的广义准对称变换。

根据定理1可以得到系统的守恒量为

4 结语

研究了时间尺度上相空间中变质量非完整系统及其相应变质量完整系统的Noether对称性，给出了系统的广义Noether等式，并通过广义Noether等式和限制方程给出了系统的Noether广义准对称性的定义，进一步得到系统的守恒量。该方法可推广到时间尺度上变质量系统Appell方程等的对称性研究中。