风力发电机主轴轴承的温度特性分析*
李 聪
(西南科技大学 制造科学与工程学院,四川 绵阳 621010)
0 引 言
风力发电机主轴轴承是支承旋转主轴的关键零部件,其承载能力和寿命对风力发电机的正常、高效运转起着至关重要的作用。 该主轴轴承承受较大的变载荷,轴承运转时滚动体和内外圈之间摩擦剧烈,接触面间产生的热量如果不能及时传递出去,将导致轴承温度过高并加快材料失效。 因此,对脂润滑轴承温度场的研究具有重要的工程意义。
近年来,国内外学者对各种应用背景下各类轴承的温度分布进行了广泛研究。 欧阳牧英等[1]对主轴和支承主轴的4 个轴承进行了有限元热计算,用接触式热电偶探头对待测点温度进行实时测量,发现温度的计算误差约为6%。 李小萍等[2]进行了环下润滑轴承的有限元传热仿真,发现供油温度是轴承温升的主要影响因素。 李梦阳等[3]应用CFX 软件对静压轴承系统进行耦合传热计算与分析,研究发现轴承的温升随轴承转速的增大而线性增加;轴承端面通过向外界排油而散发了轴承产生的大部分热量。
目前的轴承传热研究集中于喷油润滑和油气润滑工况,而轴承腔中润滑脂传热对轴承温度场影响的研究很少;较多地采用四面体网格或混合网格,很少采用相邻几何体的界面上网格节点位置相同的六面体网格(即共形网格),使得网格质量欠佳。
因此,采用ICEM CFD 软件中的分块法来生成全六面体的共形网格,建立了轴承及其流体域、主轴和轴承座的共轭传热计算模型,开展各运转工况下的数值计算,分析了轴承系统的温度分布规律,以及轴承转速、润滑脂填充量和轴向载荷对各区域最高温度的影响。 该研究可为风力发电机主轴轴承的与温度相关的设计和分析(如轴承寿命分析)提供参考依据。
1 热边界条件
1.1 轴承产热条件
在轴承运转时,各零件在接触区域受到接触应力作用,且各零件间存在相对运动,使得在零件的接触区域发生着摩擦产热现象。 使用轴承整体生热法,对所研究的圆锥滚子轴承生热率进行计算[4]。
按照该方法,轴承的总摩擦力矩M为:

式中:M0为受润滑脂粘度和内圈转速影响的摩擦力矩;M1为受载荷影响的摩擦力矩。
在该轴承的运转工况下,υn>2 000 mm2·r/(s·min),此时摩擦力矩M0为:

式中:υ为基础油在工作温度时的粘度;n为内圈转速;f0为受润滑剂和轴承类型影响的系数;dm为轴承节圆直径。
受载荷影响的摩擦力矩M1为:

式中:f1为受到轴承所受载荷和轴承类型影响的系数;P1为计算负荷。
由轴承中的摩擦损耗转化而来的轴承生热率N为:

式中:n为内圈转速;M为轴承总摩擦力矩。
在摩擦最剧烈的滚动体与滚道的接触面的附近薄层施加体生热率。 在热量的分配上,将轴承总生热量平均分配到滚动体与内圈、滚动体与外圈的接触区域,再把接触区域的生热量平均分配到滚动体和套圈表面,即与滚动体柱面接触的内圈滚道面、滚动体柱面和外圈滚道面的生热量比例为1 ∶2 ∶1[4]。
1.2 对流换热条件
当流体流经零件表面时,会发生对流换热现象,在流体与零件的接触表面上热流量Φ为[5]:

式中:h为对流换热系数;A为流体与固体间的换热表面积;Δtm为流体与换热表面之间的平均温差。
对流换热系数hx表示为[5]:

式中:Nux为努塞尔数;λ为流体的热导率;x为特征长度。
处于静止状态的轴承外圈和轴承座表面与外界空气进行着自然对流,其中的对流换热关联式为[5]:

式中:C和n为由实验确定的常数;Gr和Pr为格拉晓夫数和普朗特数,其定义为[5]:

式中:η为外界空气的动力粘度;cp为外界空气的定压比热容;α为外界空气的体积膨胀系数;Δt为换热表面与不受表面温度影响的空气之间的温度差;l为特征长度;υ为外界空气的运动粘度。
在传热计算中,零件表面的温度是实时变化的。上述公式表明,自然对流的换热系数是零件表面温度的函数。 为了提高计算精度,在Fluent 软件中采用了上述函数关系以表达式的形式使用。
轴承运转时,内圈、保持架和主轴的表面与外界空气进行着强制对流,其中转动圆柱面的对流换热关联式为[6]:

式中:ReD为雷诺数;ω为零件的角速度;d为圆柱直径。
同时对应的旋转端面与外界空气之间的对流换热系数为[6]:

式中:m为表征圆盘径向温度分布的常数,取m=2。
轴承运转时,轴承内表面与流体域中两相流进行着对流传热,由于轴承结构不规则,以及表面和流体的温度均不确定,其中的对流换热系数难以确定。 文中采用目前学术界对这类问题的处理方法,在流体域与固体域的接触表面建立了热耦合的界面,以共轭传热的方式计算其中的传热量。
2 数值计算模型
2.1 几何模型
所研究的圆锥滚子轴承FD-306/1270 是4.5MW风力发电机的主轴后轴承,其主要技术参数如表1 所列。 依据轴承的结构尺寸,在NX 软件上建立了轴承、流体域、主轴和轴承座的三维模型,固体域的剖视图如图1(a)所示。 为了提高网格质量和计算精度,并减少计算量,忽略滚动体与保持架支柱之间的径向间隙区域,将滚动体和保持架合并为一个几何体;将内圈和主轴、外圈与轴承座分别合并为一个几何体,简化后固体域的三维剖视图如图1(b)所示,于是轴承流体域的三维剖视图如图1(c)所示。

图1 计算域的几何模型
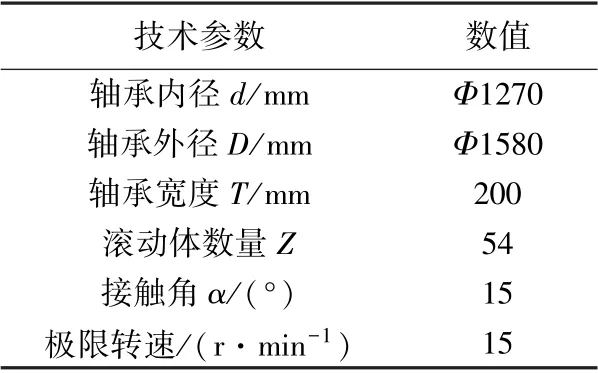
表1 轴承FD-306/1270 技术参数
2.2 网格模型
为了获得较高的网格质量和可接受的网格量,采用ICEM CFD 软件中的分块技术对三维模型进行六面体网格划分。 建立了相邻几何体的界面上网格节点位置相同的共形网格,以减少求解数据通过界面传递时的误差。 建立的网格模型如图2 所示,其包含1 169 964个六面体单元,最低正交质量达到0.34,最低偏斜度达到0.45。

图2 流体域、轴承及其连接件的网格模型
2.3 数值计算设置
基于轴承系统共轭传热的特征,在Fluent 软件中进行如下的计算设置。
(1) 选择VOF 模型来解决轴承腔中润滑脂与空气间的相界面捕捉问题。 在该主轴轴承中,润滑脂的填充量一般为轴承内腔容积的60%~80%[7],其它空间被空气填充。 设置空气为可压缩的主相,润滑脂为不可压缩的次相。 对润滑脂的粘度使用文献[8]中的Herschel-Bulkley 模型参数。 采用克服了其它k-ε模型不足的Realizable k-ε 湍流模型。
(2) 按照前文所述,在相应的面区施加产热和散热边界条件。 在计算零件表面与外界空气间的对流传热时,考虑了各零件转速的影响。
(3) 由于文献[9]使用热流网络法计算高速轴承的温度场时,未考虑轴承零件的运动对润滑脂分布和传热的影响,通过试验验证,发现该处理方法的可靠性较好,所以设置各零件均处于静止状态。
(4) 采用SIMPLEC 算法进行数值求解,采用有界二阶隐式的瞬态格式,以获得较高的计算精度和计算稳定性。 对密度、动量、体积分数、k、ε 和能量的离散,均采用精度较高的二阶迎风格式。
(5) 设置流体域内初始压力为标准大气压,计算域中初始温度为45 ℃,初始状态时流体保持静止,润滑脂和空气以一定的体积分数均匀地填充到流体域中。 设置连续性方程、动量方程、能量方程、湍流输运方程和体积分数方程的残差分别为10-4、10-5、10-7、10-3和10-5。
3 计算结果分析
3.1 温度场特性分析
对轴承转速为12 r/min、轴向载荷为2 101.93 kN以及润滑脂填充比例为70%工况下的轴承系统进行了共轭传热计算。 图3、4 是不同轴截面上的温度云图。 图中的信息显示,从滚动体表面、到内外圈滚道表面、再到内外圈、主轴和轴承座与外界空气接触的表面,温度呈现出逐渐降低的趋势。 这是因为热源被施加在滚动体柱面和内外圈滚道上,散热条件被施加在零件与外界空气接触的表面,热量从产热区域向散热区域传递的过程,也是从高温区域向低温区域传递的过程。 图3、4 的信息也显示,滚动体的平均温度最高,流体域的平均温度次之,外圈的平均温度更低,内圈的平均温度最低,现对其原因作如下分析。

图3 未经过滚动体的轴截面上的温度云图
由于润滑脂的热扩散率(8.32×10-8m2/s)小于空气(2.3×10-5m2/s)和轴承钢(1.02×10-5m2/s)的热扩散率,流体域中润滑脂的含量(70%)大于空气的含量(30%),在润滑脂和空气均匀分布的条件下,需要润滑脂来形成有效的传热路径,这使得流体域的热扩散率比滚动体的更小,滚动体热源区域的温升向流体域传递的速率比向滚动体传递的速率慢[5],使得流体域的平均温升小于滚动体的平均温升,又由于它们的初始温度相同,所以流体域的平均温度小于滚动体的平均温度。
由于流体域中润滑脂和空气的热导率(0.147 和0.026 W·m-1·K-1)远小于固体材料轴承钢的热导率(39.05 W·m-1·K-1),流体的传热效果较差,使得流体域吸收较多的滚动体产热量;又由于外圈能将热量向体积更大且与外界空气的散热面积更大的轴承座传递,从而流体域的平均温度高于外圈的平均温度。 由于与外圈相连的轴承座的体积以及轴承座与外界空气间的散热面积均比与内圈相连的主轴的体积和散热面积更小,使得外圈的传热条件相对较差,从而外圈的平均温度比内圈的平均温度更高。

图4 经过滚动体的轴截面上的温度云图
图5 是轴截面上外圈和轴承座的温度云图。 图中的信息显示,在热量传递的路径上,外圈的温度梯度普遍大于轴承座的温度梯度。 因为外圈垂直于传热方向的面积比轴承座的更小,外圈的导热热阻(δA-1λ-1)更大[5],这可能使得外圈任意位置的吸热量与沿着传热方向的传热量的比值比轴承座的普遍更大,从而在传热方向的单位距离上外圈温度降低得较多,使得外圈的温度梯度普遍更大。

图5 轴截面上外圈和轴承座的温度云图
图6 是轴截面上内圈和主轴的温度云图。 图中的信息显示,在热量传递的路径上,内圈的温度梯度普遍大于主轴的温度梯度。 如前文所述,因为内圈垂直于传热方向的面积比主轴的更小,内圈的导热热阻(δA-1λ-1)更大,从而在传热方向上内圈的温度梯度普遍更大。

图6 轴截面上内圈和主轴的温度云图
图7 是轴截面上滚动体和保持架的温度云图。图中的信息显示,滚动体的轴向中心区域的温度最高,从中心区域沿着滚动体轴线方向,依次通过滚动体端面、保持架支柱和保持架,温度呈现出逐渐降低的趋势。 这是因为滚动体柱面是产热面,与外界空气接触的保持架部分表面是散热面,而且与滚动体和保持架接触的流体域的传热条件较差。 图中的信息也显示,在热量传递的路径上,温度梯度呈现出先增大后减小的趋势。 如前文所述,在传热的路径上,温度梯度先增大后减小的趋势与垂直于传热方向上的面积先减小后增大的趋势有一定的关联。

图7 截面上滚动体和保持架的温度云图
3.2 轴向载荷对区域最高温度的影响
图8 是在轴承转速为12 r/min、润滑脂填充比例为70%和不同轴向载荷的工况下各区域最高温度的结果。 图中的信息显示,从最高温度来看,滚动体的最高,流体域的稍低,外圈的更低,内圈的最低,这体现了各区域最高温度与平均温度之间的正相关关系。当轴承受到线性增加的轴向载荷时,通过整体法计算出的总产热量也线性增加,使得各区域的最高温度均近似线性升高。 然而流体域和滚动体的最高温度相对于轴向载荷的斜率均比内圈和外圈的更大。 因为随着轴承所受轴向载荷的增大,轴承的总产热量增加,内外圈滚道面的产热量基本都向低温的、传热和散热条件均较好内外圈、主轴和轴承座传递,但是润滑脂和空气的热导率远小于轴承钢的热导率,使得流体域的传热受到阻碍,流体域、滚动体和保持架吸收的滚动体产热量占滚动体总产热量的比例变大,内外圈、主轴和轴承座吸收的滚动体产热量占滚动体总产热量的比例变小,从而形成如图所示的斜率差异。
3.3 轴承转速对区域最高温度的影响
图9 是在轴向载荷为2 101.93 kN、润滑脂填充比例为70%和不同轴承转速的工况下各区域最高温度的结果。 对比图8、9 发现,在转速为9 r/min、轴向载荷为2 101.93 kN 的工况下和转速为12 r/min、轴向载荷为1 516.22 kN 的工况下,各区域的最高温度对应地几乎相等,而且在转速为15 r/min、轴向载荷为2 101.93 kN 的工况下和转速为12 r/min、轴向载荷为2 687.64 kN 的工况下,各区域的最高温度也对应地几乎相等;转速为12 r/min、轴向载荷为2 101.93 kN 的工况是两图中的共有工况,其对应温度自然相等。 因为经过使用轴承整体生热法计算各工况下的总产热量,发现在上述的对应工况下轴承总产热量相差很小,如表2 所列;同时在对应工况下轴承转速的差异较小,使零件向外界空气的散热差异较小,使得在对应工况下计算域中相同位置的传热量相差很小。

图8 轴向载荷对区域最高温度的影响

图9 轴承转速对区域最高温度的影响
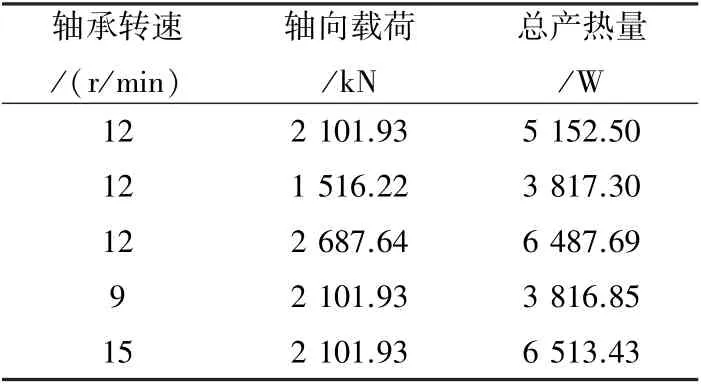
表2 轴承的总产热量
3.4 润滑脂填充量对区域最高温度的影响
图10 是在轴向载荷为2 101.93 kN、轴承转速为12 r/min 和不同润滑脂填充量的工况下各区域最高温度的结果。 由于润滑脂的热导率(0.147 W·m-1·K-1)大于空气的热导率(0.026 W·m-1·K-1),当润滑脂的填充量增大时,流体域的导热性变好,较高温度的流体域、滚动体和保持架中更多的热量能通过流体域传递到内外圈、主轴和轴承座,使得流体域和滚动体的最高温度均降低,内圈和外圈的最高温度均升高,如图10 所示。 由于流体域的体积比固体域的小,而且润滑脂的推荐填充量的范围较小[7],使得润滑脂填充量对流体域的吸热和传热特性的影响较小,所以各区域最高温度的变化量均较小。
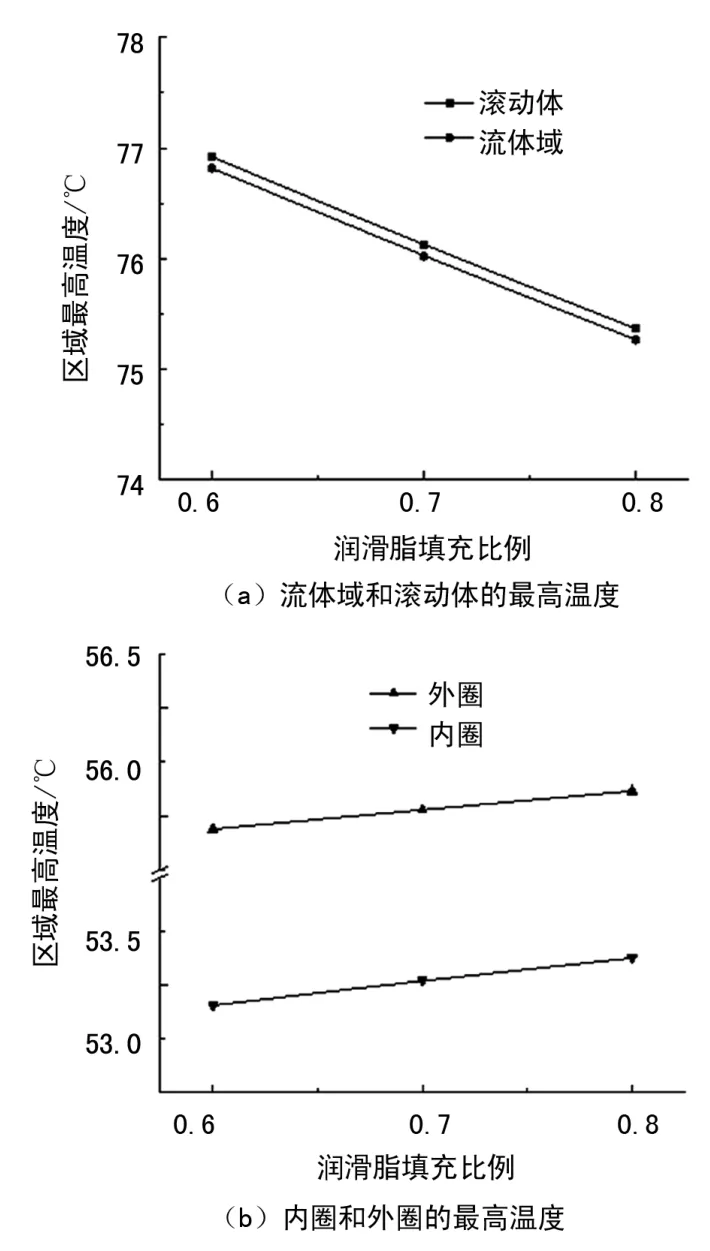
图10 润滑脂填充量对区域最高温度的影响
4 结 论
应用ANSYSFluent 软件进行了风力发电机主轴轴承系统的共轭传热数值计算和结果分析,得出了如下主要结论。
(1) 从滚动体表面、到内外圈滚道表面、再到内外圈、主轴和轴承座与外界空气接触的表面,温度呈现出逐渐降低的趋势。 从最高温度来看,滚动体的最高,流体域的稍低,外圈的更低,内圈的最低。
(2) 在热量传递的路径上,外圈的温度梯度普遍大于轴承座的温度梯度,内圈的温度梯度普遍大于主轴的温度梯度,滚动体和保持架的温度梯度呈现出先增大后减小的趋势。
(3)随着轴向载荷(或轴承转速)的增大,流体域和滚动体的最高温度均比内圈和外圈的升高得更快。 当润滑脂的填充量增大时,流体域和滚动体的最高温度均降低,内圈和外圈的最高温度均升高。 该研究为风力发电机主轴轴承的与温度相关的设计和分析(如轴承寿命分析)提供了参考依据。

