自我重复取样技术与多项式定理在年龄-龄期两性生命表研究中的应用

李建宇,陈燕婷,傅建炜,史梦竹,齐 心,尤民生

(1.福建省农业科学院植物保护研究所，福建省作物有害生物监测与治理重点实验室,福州 350013;2.福建省农业科学院农业质量标准与检测技术研究所,福州 350003;3.福建农林大学应用生态研究所,闽台作物有害生物生态防控国家重点实验室,福州 350002;4.山东农业大学植物保护学院,山东泰安 271018)

生命表是一个由种群所有个体的生存、发育和繁殖等数据组成的综合数据集，是害虫治理与生态学研究中最重要的工具之一(齐心等,2019;Chietal.,2020;Taghizadeh and Chi,2022)。早期普遍使用的传统雌性特定年龄生命表(Euler,1760;Lotka,1907;Birch,1948;Carey,1993)由于未能描述龄期分化(即变态)，且忽略了雄性个体对种群增长与其对捕食、寄生和取食等效能的贡献，因而无法准确预测种群的增长，同时也限制了生命表在生态学理论中的发展及其在害虫防治中的实际应用(Huang and Chi,2012)。相对而言，年龄-龄期两性生命表(简称“两性生命表”)(Chi and Liu,1985;Chi,1988)在理论、数据分析以及实际应用中不仅能较准确地描述昆虫种群的龄期分化与两性差异，同时也能更好地应用于种群预测和生物防治等研究。因为两性生命表的上述优点，研究者能正确分析昆虫不同龄期间与雌雄两性间的各种差异，例如捕食率(或寄生率与取食量)差异、对药剂敏感性的差异等对种群生命表的影响，这使得生命表理论得以进一步发展，并能用于种群相互关系的研究。蒲蛰龙(1989)主编的《农作物害虫管理数学模型与应用》已将Chi和Liu(1985)的两性生命表论文翻译并纳入书中。普林斯顿大学出版社(Princeton University Press)出版的专著《Population Harvesting》(Getz and Haight,1989)也详细介绍了Chi 和 Liu(1985)的两性生命表理论。在国内，吴坤君等(1994)首次将两性生命表用于粘虫Mythimnaseparata的生命表研究，并指出其优点。近年来国内外学者普遍采用两性生命表进行相关研究(胡昌雄等,2021;Naeemetal.,2021;谢艳兰等,2021;Amir-Maafietal.,2022;Iqbaletal.,2022)。自1990年后，为方便使用者运用两性生命表理论而创制并不断更新的数据处理软件TWOSEX-MSChart(Chi,2022)，因为操作简便，多数研究人员均能快速掌握其使用方法，并且从软件输出的结果中获取相关研究需要的数据，用于理论的研究和实践推广应用。然而，由于有许多研究人员对于两性生命表软件中所使用的生态学理论与数理统计理论的理解有限，造成在论文撰写和应用分析时出现不准确甚至错误的现象。本文详细阐述两性生命表所使用的自我重复取样(bootstrap)技术与多项式定理(multinomial theorem)的原理和运用，旨在帮助国内昆虫学和生态学的研究人员深入理解两性生命表中的基本原理，更好地将其运用于相关科研工作中，进而提升科学研究水平。为了方便解释bootstrap技术和多项式定理在两性生命表应用中的原理，更直观地展示相关公式模拟的结果，本文选用本课题组未发表试验数据进行相关模拟分析并作图。

1 常用统计方法与bootstrap统计方法比较

1.1 常用统计方法

在科学研究中，为了对数据进行数理统计分析，研究人员会在相同条件下进行多次重复试验，再计算各重复数据的均值与标准误用于分析。常用统计方法均以正态分布为前提，但是大多数试验数据为非正态分布，如用50头昆虫研究繁殖力或寿命时，其频率分布(frequency distribution)一般是非正态分布(图1)。

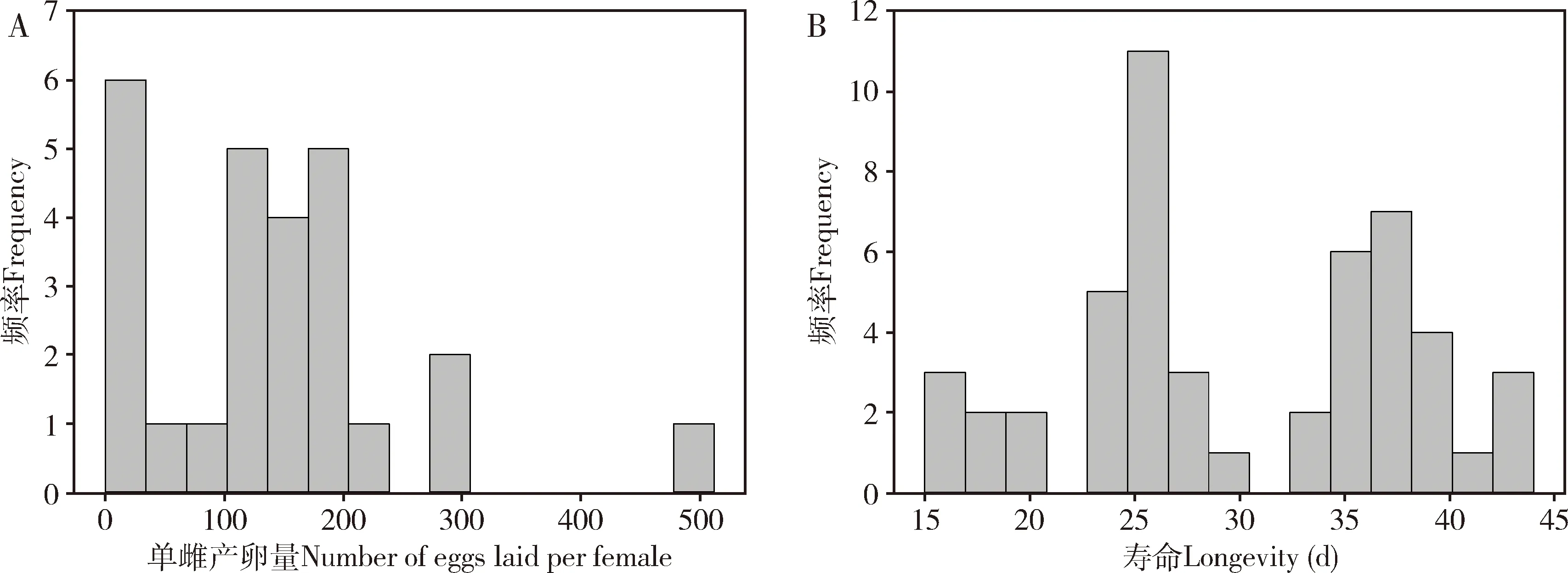
图1 LC30浓度虫螨腈处理后木瓜秀粉蚧的繁殖力(单雌产卵量)(A)和寿命(B)的频率分布Fig.1 Frequency distribution of the fecundity (number of eggs laid per female)(A) and longevity (B) of Paracoccus marginatus after treatment with LC30 of chlorfenapyr

常用统计中用公式(1)～(3)计算50头试虫的平均寿命与标准误，若其中有30头雌虫，则可用30头雌虫的繁殖率计算平均繁殖率与标准误。

(1)

式中Xi为第i头试虫的寿命或繁殖率。

(2)

(3)

1.2 Bootstrap统计方法

Bootstrap是一个很通用的工具，用来估计偏差、标准误和置信区间。它是由Efron(1979)提出的一种统计方法，根据原始试验样本重复抽取样本信息，不需要数据分布假设，即可对数据总体的分布特性进行统计和推断。Efron和Tibshirani(1993)较为系统地介绍了bootstrap技术的理论成果。“Bootstrap”一词来自短语“to pull oneself up by ones bootstraps”，这个短语源自西方童话故事“The Adventures of Baron Munchausen《吹牛大王历险记》”(Raspe,2017)。故事中的吹牛大王说他有一次掉到了很深的湖底，最后他通过拎着自己的鞋带将自己从湖底救出(Johnson,2001)。这个故事比喻不靠外界力量，只靠提升自己的性能，就能达到目标。同样地，统计学中的bootstrap技术完成了似乎不可能的事情，即利用自我重复取样来估计未知概率统计量的统计特性。

昆虫学、生物学与生态学等研究中有许多数据属于非正态分布，常常无法确定其正态性，因此难以获得正确的标准误。此时，研究人员只能采用增加大量样本，或者采用数学方法对数据进行正态化转换，但是这些方法往往有其缺点，或者得到的结果依然不是很理想。Bootstrap技术的出现，则较好地解决这个问题。目前bootstrap技术的方法和理论已在金融、经济、生物和医学等领域广泛应用(MacKinnon,2002;赵亮等,2010;Amir-Maafietal.,2022)。

2 生命表数据分析

若以50粒卵开始做生命表研究，可以用50个个体的存活率与繁殖率计算内禀增长率、周限增长率、净增殖率和平均世代时间等。

两性生命表中净增殖率(R0)公式为

(4)

其中，k为龄期数，sxj为新生个体存活到年龄x与龄期j的概率，fxj为个体在年龄x与龄期j时的平均繁殖率。若只考虑年龄时，lx为新生个体存活到年龄x的概率，mx为个体在年龄x时的平均繁殖率。内禀增长率(r)计算公式为

(5)

用矩阵研究种群增长时，Lewis(1942)的种群周限增长率(λ)计算公式为

λn+1-f0λn-s0f1λn-1-s0s1f2λn-2-…-s0s1…sn-2fn-1λ-s0s1…sn-1fn=0

(6)

其中，fx≥0,sx>0，sx为年龄x的个体存活到x+1的概率，fx为个体在年龄x时的平均繁殖率(Lewis原公式的起始年龄为1，公式6的起始年龄为0)。因为周限增长率的公式较长，一般论文中只列出内禀增长率的公式，再用r与λ的关系式表示λ=er。在计算机普及之前，使用这两个公式计算一个生命表的内禀增长率与周限增长率已十分困难，因为必须使用e与大数值的指数，因此有许多学者发展各种简化方法，例如Howe(1953)以及Wyatt和White(1977)等。由于这些简化方法已被证明会导致错误结果(Mirmohammadietal.,2009;Saskaetal.,2021)，本文不再对这些简化方法的错误进行赘述。

由于50个个体的数据用一般统计方法计算只能得到一个内禀增长率、周限增长率、净增殖率和平均世代时间，无法计算标准误。如果用一般方法里的重复概念，需要做多个重复，即必须做多个生命表。因为生命表研究需要大量的人力、时间和空间，若用一般方法里的重复概念，将耗费大量时间、人力和经费，因此很少有人用“重复”的概念计算生命表各个参数的标准误。为了解决此问题，Meyer等(1986)介绍将jackknife与bootstrap技术用于计算种群增长率的标准误。这两种方法的使用均须依赖计算机。早期由于个人计算机的性能较差，使用bootstrap技术计算种群增长率的标准误需要数日的时间，因此应用较多的是jackknife方法(Chi and Getz,1988)。随着计算机性能的提升，以及Huang和Chi(2013)证明jackknife方法并不适合用于生命表研究，bootstrap技术成为目前普遍采用的方法。

3 两性生命表中bootstrap的方法与优势

3.1 两性生命表中采用bootstrap技术的原理与估计种群参数标准误

在使用bootstrap技术计算两性生命表种群参数时，从种群中随机抽n个个体进行归还取样，其中n通常就是生命表种群的起始个体数。因为是归还取样，每一个个体的数据可能被反复选取，也有些个体可能没有被选到，其概念如图2所示。

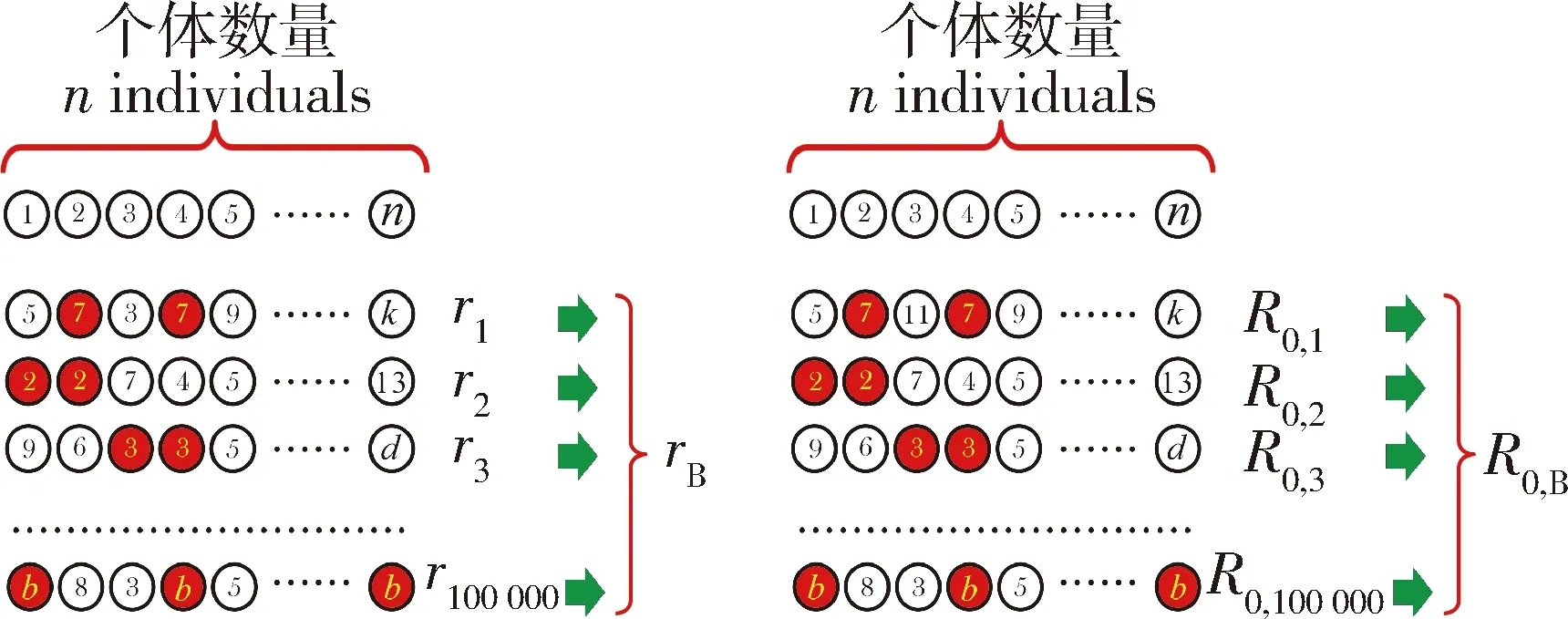
图2 Bootstrap技术原理Fig.2 Principles of the bootstrap technique R0:净增殖率Net reproductive rate;B:重复取样数Number of re-samplings.

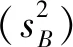
(7)

(8)

(9)

为了提高精确度与减少两次bootstrap间的差异，必须选用较大的重复取样数B值，理论上B值越大，模拟估算的方差和标准误越准确，而且每次bootstrap产生的方差较为稳定。但是，B值的设定受计算机中央处理器(central processing unit,CPU)速度与内存(random-access memory,RAM)容量的限制，设定的B值太大，计算机需要的运行时间则较长，甚至过大的B值会导致计算机无法运行。由于早年的计算机速度与内存容量有限，Meyer等(1986)推荐的B值为500～1 000。图3展示了使用1 000个和100 000个bootstrap重复获得的数据频率分布的差异。其中，图3(A)和(B)为两次1 000个bootstrap运行结果，图3(C)和(D)为两次100 000个bootstrap运行结果。显然，1 000个bootstrap重复取样的频率分布已近似正态，但在两次运行之间的频率分布仍有明显差异。在1980年代，bootstrap技术的应用受到了计算机CPU和RAM的限制，用bootstrap模拟完成需花费大约20 000 h(Hesterberg,2008)。但是，使用100 000次bootstrap技术已能产生一个可接受的正态分布(图3:C,D)，且两次之间的差异较小，估计值的方差与标准误较为稳定。由于bootstrap是一个重复归还取样(sampling with replacement)的过程，当n>10，B=100 000时，每个bootstrap样本都会产生不同的个体组合，种群参数的平均值、方差和标准误都可能不同。因此，一般使用bootstrap时，没有所谓的最优或最适当B值。所需的bootstrap数量取决于生命表数据(个体数、龄期数、寿命和个体间的差异等)，当个体之间的差异越大，bootstrap的数量就应该越高。通过反复的试验，目前TWOSEX软件预设的B值是100 000，这样的设定对绝大多数的昆虫生命表研究都能提供很好的结果。使用bootstrap技术，通过100 000次取样后，所得到的种群参数一般呈正态分布，且方差较小(Efron and Tibshirani,1993;Yuetal.,2013)。随着计算机运算速度的提升，100 000次bootstrap取样在几分钟内即可完成。自2013年以后，TWOSEX-MSChart软件不再提供jackknife方法，仅提供bootstrap技术供研究人员使用。

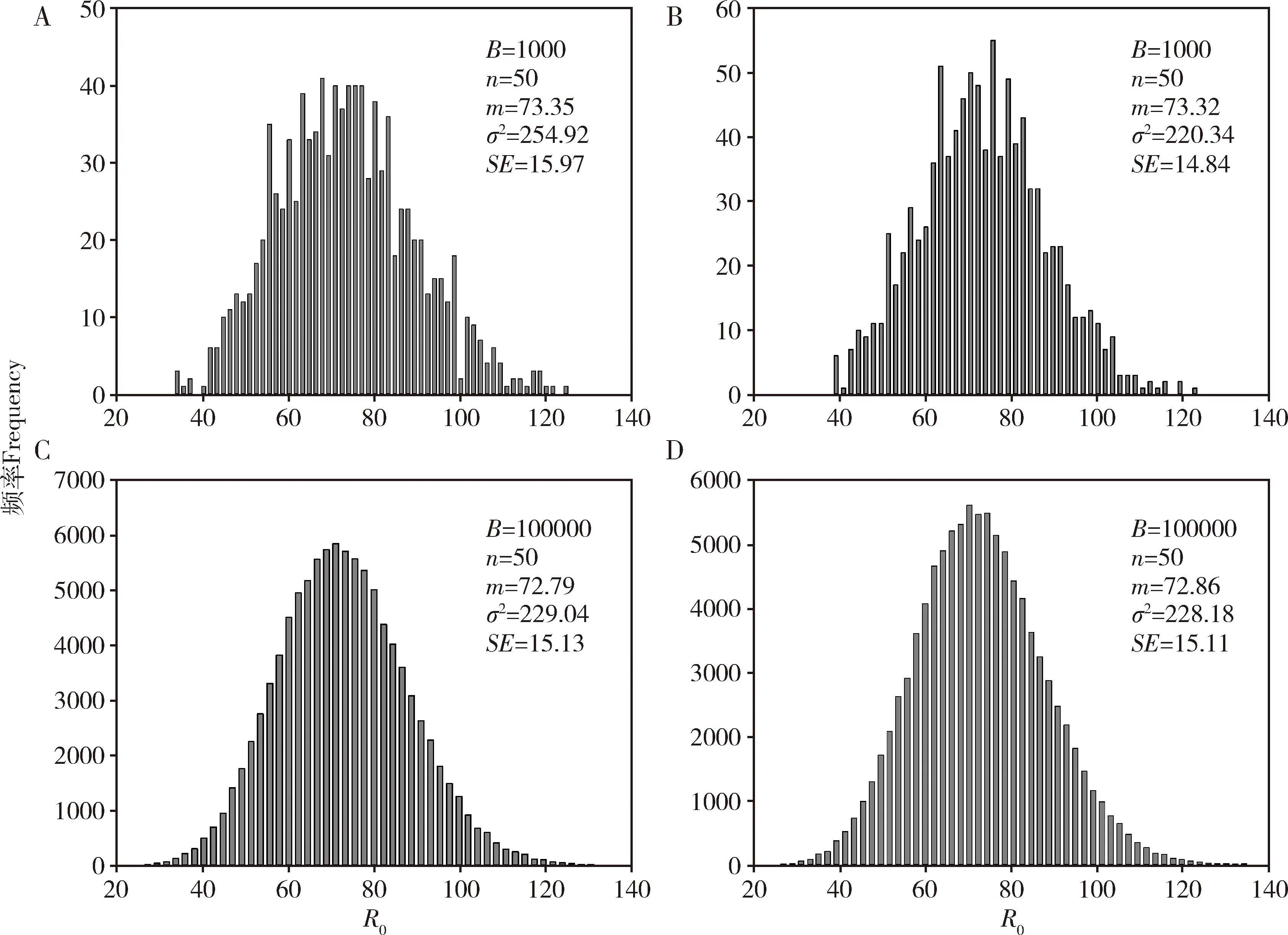
图3 Bootstrap 1 000次重复取样(A,B)和100 000次重复取样(C,D)获得的莲草直胸跳甲种群净增殖率(R0)估计值的频率分布Fig.3 Frequency distribution of bootstrap estimates of the net reproductive rate (R0) of Agasicles hygrophila by using 1 000 bootstrap re-samplings (A and B) and 100 000 bootstrap re-samplings (C and D)B:重复取样数Number of re-samplings;n:个体数Number of individuals;m:平均值Mean;δ2:方差Variance;SE:标准误Standard error.图4同。The same for Fig.4.

3.2 采用bootstrap估算一般统计参数标准误

Bootstrap技术不但可以用于估算种群参数的方差与标准误，也可以用于一般统计值(TWOSEX软件中的G.Gen.boot)。图4为应用bootstrap技术估算繁殖力和寿命的标准误。从图4可看出bootstrap技术估算的数据呈正态分布。因此，无论将bootstrap技术用于估算种群参数或一般统计值，其结果一般都符合中心极限定理(central limit theorem)，也能准确展示种群的变异性(齐心等,2019)。

图4 LC30浓度虫螨腈处理后木瓜秀粉蚧的平均繁殖力(A)和平均寿命(B)的频率分布Fig.4 Frequency distribution of the mean fecundity (A) and mean longevity (B) of Paracoccus marginatus after treatment with LC30 of chlorfenapyr

3.3 Bootstrap技术中用paired bootstrap test比较不同处理间的差异

在TWOSEX-MSChart软件中paired bootstrap test检验的结果有下列3种方式呈现：(1)t置信区间(假设结果是正态分布)；(2)Bootstrap percentile (百分位置信区间)(基于实际取样结果)；(3)P值基于bootstrap样本中差异显着的bootstrap样本数。因为t置信区间是基于正态分布的假设，而bootstrap百分位置信区间是基于随机取样的，所以它们可能是不同的。虽然大多数生物学和生态学数据为非正态分布，但是当B足够大时，bootstrap样本平均值的分布一般是正态的。因此，需要大量的重复取样(B=100 000)才能保证估算值的稳定。如果bootstrap结果是正态分布的，则t置信区间与bootstrap置信区间将非常相近。一般而言，3种方法的显着性检验结果是一致的。只有在极端情况下才会出现不一致的结果。当3种结果不一致时，研究人员必须依据数据妥善判断与解释(Weietal.,2020)。

3.4 将相同的自我重复取样样本(same bootstrap samples)用于相关的分析

3.4.1孵化率:由于每次bootstrapping都会产生不同的结果，TWOSEX软件将100 000个bootstrap样本保存于一个纯文字文件中。若要明确卵的孵化率是否会因雌虫的年龄而发生变化，使用者可以将每头雌虫每日的“总产卵量”与“孵化卵量”分别制作成两个生命表，然后选择用相同的bootstrap样本分析总产卵量和孵化卵量之间的关系，并估计整体孵化率(hatching rate)的标准误。如果不使用相同的bootstrap样本，总产卵量生命表的第x个bootstrap样本的平均繁殖率可能低于孵化卵量生命表的第x个平均繁殖率，导致卵孵化率大于1，这是错误的。此外，如果文件A包含每个个体每天的总产卵量，文件B包含每天的孵化卵量，如果文件B只有少数个孵化卵，那么研究者可能会面临一个问题，即文件B的样本得到的R0=0。这时，必须先用文件B运行bootstrap，然后使用相同的bootstrap样本运行文件A。为了获得准确的结果，这些细节都是在使用bootstrap技术时需要考虑的。

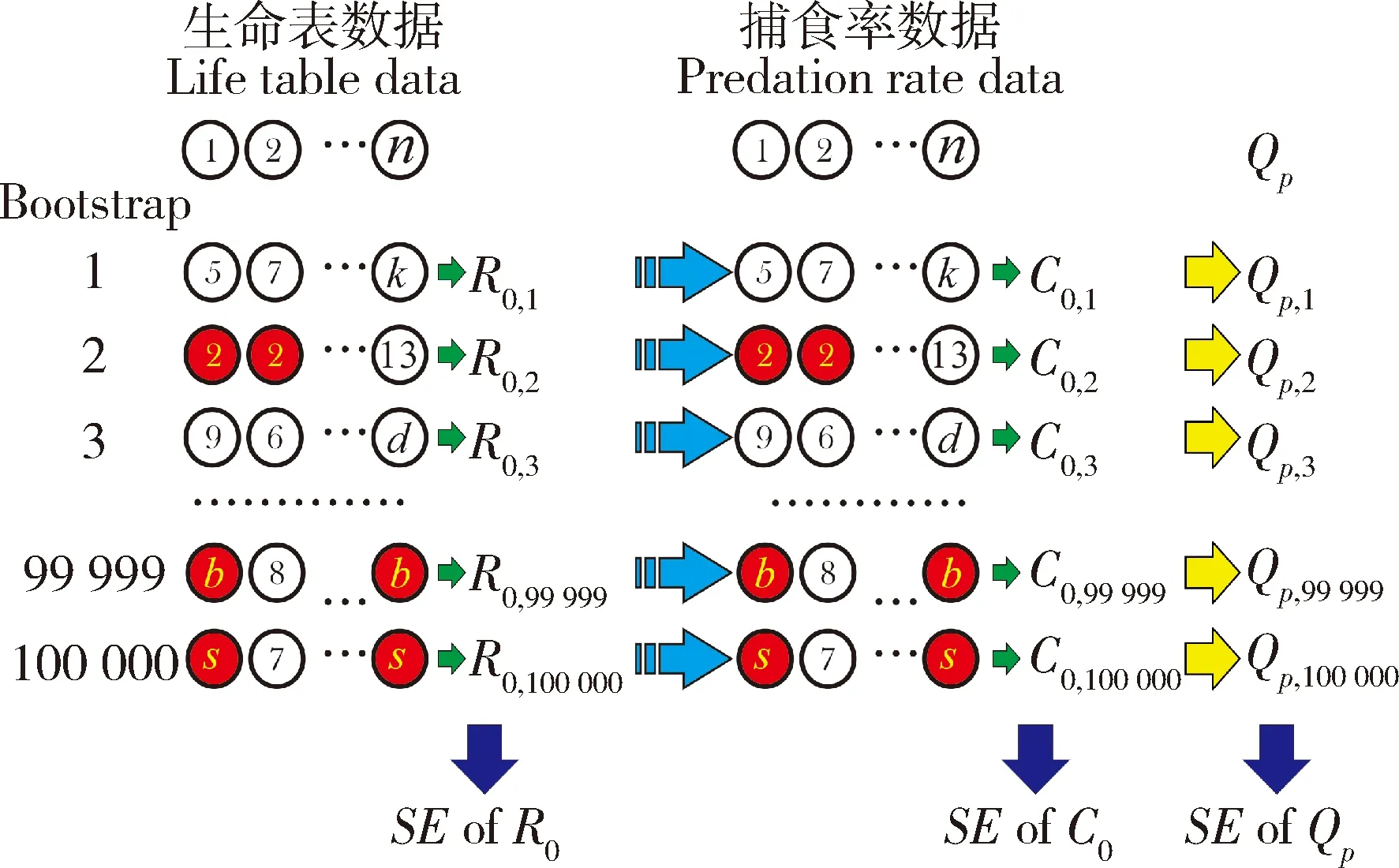
图5 采用相同bootstrap样本计算转换率(Qp)的标准误原理Fig.5 Principles of calculating the standard error of transformation rate (Qp) by using the same bootstrap samples首先用害虫的生命表数据计算净增殖率(R0)，然后用相同的bootstrap样本计算天敌的净捕食率(C0)，因为样本相同，就可以计算天敌每产一个卵需要捕食害虫的数量，从而计算转换率(Qp)及其标准误。Firstly,the net reproductive rate (R0) was calculated using the life table data of insect pest.The same bootstrap samples were used to calculate the net predation rate (C0) of natural enemy.Then the number of prey (insect pests) required for natural enemy to produce one egg could be calculated.Finally,the transformation rate (Qp) and its standard error could be calculated.

3.4.2生命表与捕食率:生命表是种群生态学最重要的基础。生命表除了可以进行精确的害虫种群预测以外，也可以将生命表应用于天敌大规模饲养、生物防治和害虫管理等。这时，就必须把生命表和捕食率结合起来以便正确用于生物防治。当利用TWOSEX和CONSUME软件结合进行天敌种群增长预测与捕食潜能分析时，必须采用相同的bootstrap样本正确估算转换率(Qp)的标准误。图5显示了采用相同bootstrap样本计算转换率(Qp)标准误的原理，由于bootstrap技术采用的是重复随机取样，因此需要保存生命表分析中用于计算净增殖率(R0)的100 000个bootstrap样本，然后将其用于计算净捕食率(C0)的分析。CONSUME软件可以将生命表分析与捕食率正确地连接起来，以估算转换率(Qp=C0/R0)和周限捕食率(ω)及其标准误。其中，Qp描述了繁殖和捕食率之间的关系(Chi and Yang,2003)，即捕食者每产生一个子代需要捕食的猎物数。但是，高Qp值并不一定代表高捕食效能。自2013年以来，TWOSEX-MSChart(Chi,2022)便提供了估算Qp标准误的功能。

3.4.3利用bootstrap技术估算有翅蚜与无翅蚜对种群参数的贡献：若蚜虫种群中同时存在有翅型与无翅型子代，可以参考Özgökçe等(2018a,2018b)和Luo等(2022)计算两种类型对内禀增长率与净增殖率的贡献。

(10)

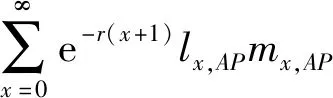
=R0,AP+R0,AL

(11)

(12)

上式中R0,AP/R0与R0,AL/R0分别为无翅子代与有翅子代对净增殖率的贡献。

在大多数蚜虫种类中，有翅蚜的比例会发生变化。例如，在春季，为了进行季节性的扩散，有翅蚜比例通常较高。同时，由于各种环境因素也会影响有翅蚜的比例(Mehrparvaretal.,2013)。因此，在计算生命表参数时，由于有翅蚜个体数量变化较大或者在种群中的比例较低，往往没有将有翅蚜包括在内(Özgökçe and Atlhan,2004;Kaydanetal.,2006;Mirmohammadietal.,2009;Mehrparvaretal.,2013;Akköprüetal.,2015)。然而，从生命表分析中排除有翅蚜意味着数据分析的不完整性和实验结果的不准确。Özgökçe等(2018a)和Luo等(2022)通过使用两性生命表方法来计算有翅蚜和无翅蚜个体对种群的贡献，利用bootstrap技术估算了发育时间、繁殖力、寿命和种群参数的方差和标准误，并进行了自我重复取样，以获得稳定的估算值。有翅蚜不仅使蚜虫能够快速扩散，同时加速了蚜虫在寄主之间传播植物病毒。因此，通过两性生命表的结果，准确预测有翅蚜的发生高峰期，有利于蚜虫的综合治理。

3.5 Bootstrap技术的优点与缺点

Bootstrap技术的优点除了上述的以外，bootstrap用于生命表研究时，是以个体为取样单位，每个bootstrap样本包含n个个体的全部特性(包括发育历期、寿命、雌性繁殖率和取食量等)。由于每个个体的上述各个特性之间不是相互独立的，而是互相关联的，使用bootstrap技术才能正确地分析数据。以性比为例，性比是生命表研究中一项常用的统计参数，在昆虫种群发展中起关键作用。使用两性生命表时，bootstrap能包含性比的变化对种群的影响。因为传统雌性生命表完全忽略雄性，使用传统雌性生命表时，即使采用bootstrap技术，也无法涵盖性比对种群参数的影响。尽管传统雌性生命表也考虑性比，但是一般性比并不能反映成虫前期存活率的差异及其对种群繁殖力的影响，因此具有相同性别比例的两个种群完全可能具有不同的适合度，所以使用传统雌性生命表将会造成诸多问题，具体可参考Huang和Chi(2011)。两性生命表包含了所有个体，在原始数据分析中采用bootstrap自我重复取样，所有bootstrap样本可能包含不同数量的雌性、雄性和在成虫前阶段死亡的个体。因此，通过使用bootstrap技术，两性生命表可以正确分析包括性比的标准误及其对种群参数的影响(Chenetal.,2018;Huangetal.,2018;Chietal.,2020)。Bootstrap技术虽有许多优点，但其仍有些缺点。例如：bootstrap技术完全依赖计算机仿真，由于其本质为随机取样，每次结果均不同，必须用较大的重复取样数以获得较精确地估计值，但重复取样数又受限于计算机CPU与内存容量的限制；此外，当bootstrap样本中仅含雄性个体时，bootstrap样本无法计算内禀增长率，这也是bootstrap的缺点之一。对bootstrap技术拟深入学习者，可参考Canty等(2006)的论文。

4 多项式定理

任何技术的背后都需要科学理论的支撑，有些技术背后的科学理论迄今尚未被发现，还有些技术的科学理论已经被证明，但是因为太难，理解的人不多。例如，原始人发明了“轮子”，但是人类有文字与数学后，才尝试了解圆周率，又经过了很久数学家才证明π为无理数。Bootstrap技术的理论基础即数学中的多项式定理(multinomial theorem)(华罗庚,1957)与概率论(probability)。

4.1 将多项式定理应用于生命表研究

为了计算bootstrapR0的理论概率或精确概率，Zhao等(2021)与Ding等(2021)首次将多项式定理应用于生命表研究。多项式定理公式为：

(a1+a2+…+an)n=

(13)

(14)

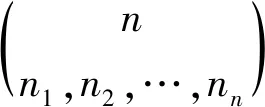
(15)

因此，利用多项式定理，可以计算出任何特定的bootstrap生命表样本的精确机率。

虽然利用多项式定理可以计算出所有可能的bootstrap生命表，对于使用100头试虫的生命表研究，有100100种取样顺序(即1.0×10200)，不同个体组成的生命表总数为4.5274×1058个，而对于使用50头试虫的生命表研究，有5050种取样顺序(即8.881784×1084)，不同个体组成的生命表总数为5.0446×1028个，对目前的个人计算机来说，仍然不可能完成所有不同组成的生命表及其机率的计算。由于bootstrap技术中的B值一般远小于Ln(亦即B≪Ln)，因此，任何一个bootstrap样本只是用计算机模拟得到的多项式定理的一小部分。在这个计算过程中，当B值较大(≥100 000)时，bootstrap样本的概率接近理论值(Dingetal.,2021;Taghizadehetal.,2022)。如果要利用多项式定理得到准确的结果，就必须在超级计算机上进行分析。

目前在两性生命表研究中受制于个人计算机的运算能力，一般只能用100 000个bootstrap样本，但仍能获得稳定可信赖的参数。图6为未进行排序的100 000个bootstrap样本的散点图，显示了采用bootstrap技术取样的随机性，当对100 000个bootstrap样本进行排序，可以得到一条平滑的曲线(图7)。由图7中可以找到0.025与0.975的置信区间(confidence interval)。若计算每个R0出现的次数，就可以做出频率分布图(图8:A)，100 000个bootstrap样本的R0频率分布接近正态分布。若把图8(A)分组合并做成50个柱状图，就会呈现类似图3或图4的形状。虽然图3与图4是一般统计教科书与一般研究人员期望的正态分布，而图8(A)是数据的真实原貌。图8(A)中，在第2.5百分位数(R0=44.94)、第50百分位数(R0=72.20)与第97.5百分位数(R0=104.16)的bootstrap生命表数量分别有13个(图8:B)、51个(图8:C)和6个(图8:D)；在100 000个bootstrap样本中，这些值的概率分别为0.00013,0.00051和0.00006。利用多项式定理计算这些bootstrap生命表的理论概率分别为1.8415×10-5,210.9188×10-5和0.7356×10-5，它们理论的次数分别约为1.8415,210.9188和0.7356，它们的差异是由于模拟 100 000 次还是非常小的比例，距离真实的多项式定理的理论值还有相当大的差距。种群的R0值为72.84，用t(1.96)计算得到的0.025和0.975置信区间分别为43.1574和102.5226。用t分布所计算的置信区间和实际取样获得的置信区间相当一致。因此，通过多项式定理显示bootstrap技术采用100 000次重复取样能得到较稳定和可靠的总体参数估计。由于昆虫、螨类等群体的高度变异性，精确估计种群增长潜力的不确定性对于害虫防治非常重要，而1 000次或者较少的bootstrap重复取样可能会错估置信区间(Akçaetal.,2015)，在种群生态学和害虫管理研究的实际应用中，这将导致害虫防治的失败。

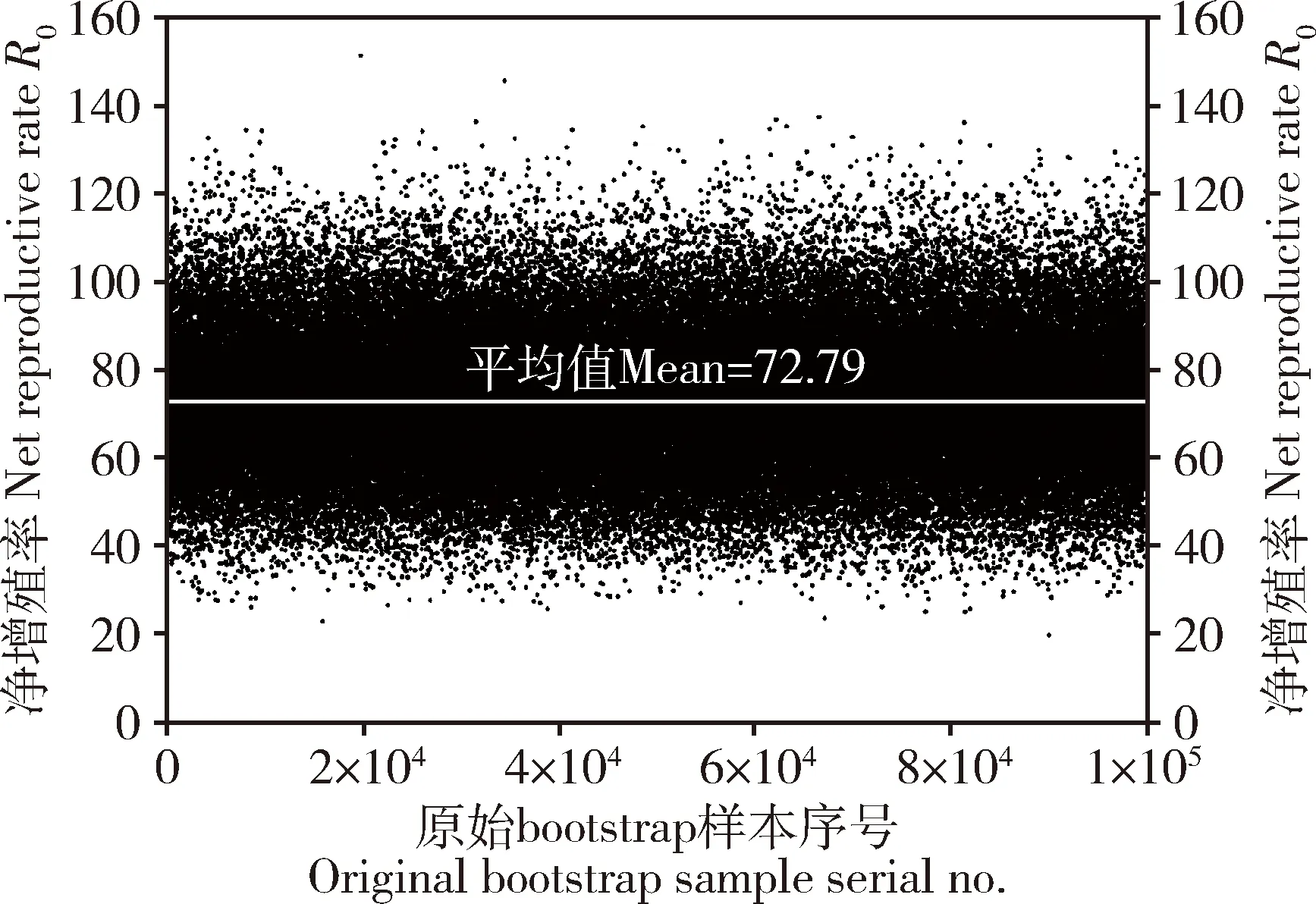
图6 Bootstrap 100 000次重复取样获得的未排序的净增殖率(R0)Fig.6 Original bootstrap results of the net reproductive rate (R0) obtained by using the bootstrap technique with 100 000 re-samplings

图7 Bootstrap 100 000次重复取样获得的净增殖率(R0)排序后的结果Fig.7 Sorted result of the net reproductive rate (R0) obtained by using the bootstrap technique with 100 000 re-samplings

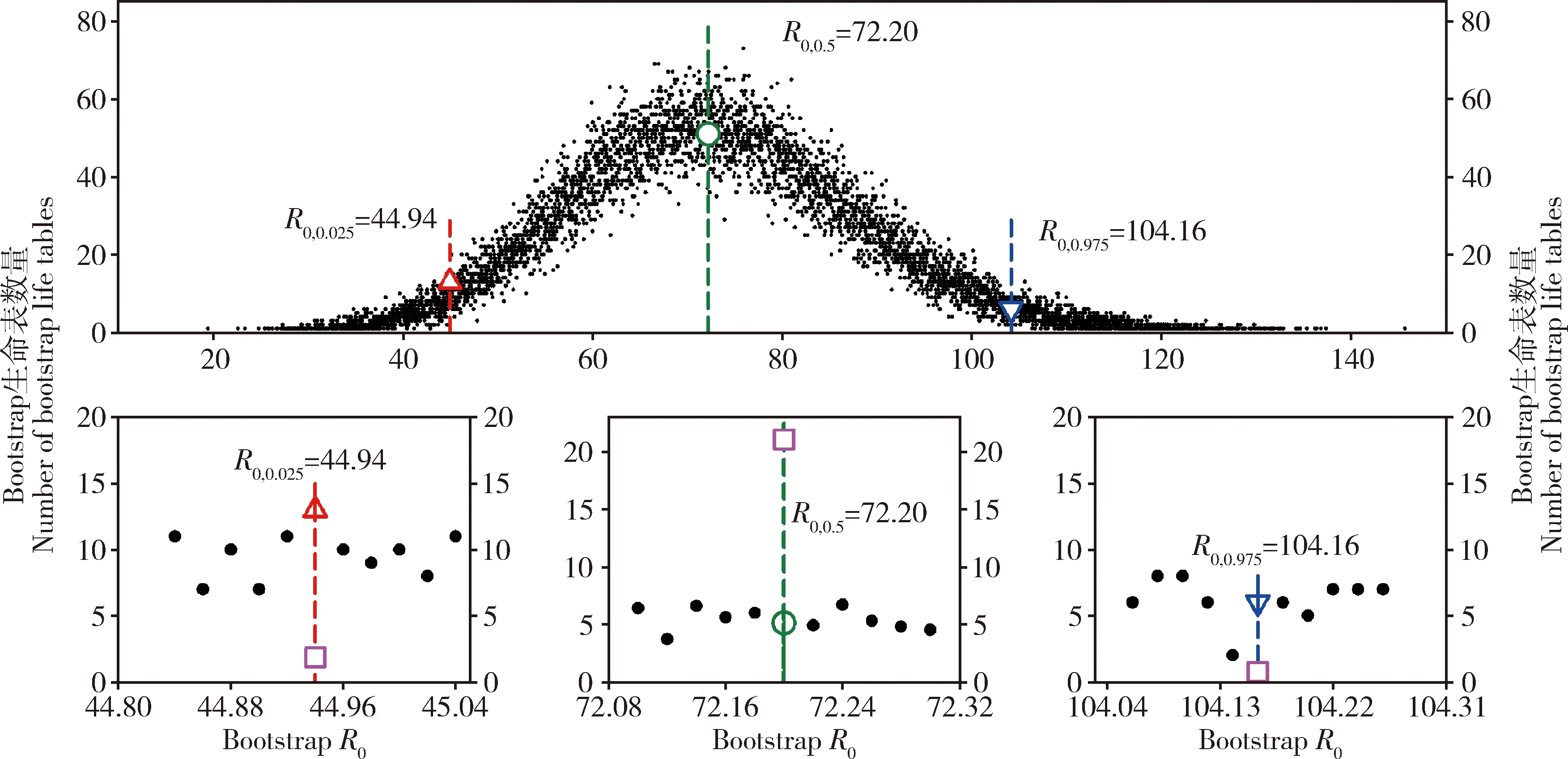
图8 Bootstrap 100 000次重复取样获得的净增殖率(R0)进行分组后的分布频率Fig.8 Frequency distribution of the net reproductive rate (R0) obtained by using the bootstrap technique with 100 000 re-samplings第2.5,50和97.5百分位的bootstrap R0对应的生命表数量分别有13,51和6个；B,C和D为这3个区域放大后的结果，粉色正方形框为多项式定理计算得到的生命表数量。The numbers of life tables corresponding to the bootstrap R0 at the 2.5th,50th and 97.5th percentiles were 13,51 and 6,respectively.B,C,and D are enlarged plots of these 3 regions.The pink squares in B,C,and D indicate the number of life tables calculated by using the multinomial theorem.

4.2 Bootstrap技术中无效bootstrap样本(ineffective bootstrap sample)的问题

对需要两性交配的昆虫而言，若一个样本中只包含雄性和在成虫前已死亡的个体(N-type)，就不能计算内禀增长率与周限增长率，则为无效bootstrap样本(ineffective bootstrap sample)。相同地，若一个样本中只包含雌性和在成虫前已死亡的个体，或一个样本只包含在成虫前已死亡的个体，都属于无效样本。当无效样本比例较高时，若在生命表分析过程中仅接受有效的bootstrap样本就会产生不现实的平均值、方差和标准误。当一个种群中因为成虫前期死亡率较高，只有少数具有繁殖能力的雌性与雄性个体，无效样本的影响就不能忽略。无效样本也反映出种群的存活概率，这是值得深入研究的问题。无效样本的计算已包含在TWOSEX-MSChart中，并已实际用于研究(Fengetal.,2020)，但因其理论较为复杂，将另文发表。

5 小结与展望

计算机模拟是理论推断和实验研究之外的重要补充工具(Pool,1992)。Chi(2000)讨论了计算机模拟的3个本质：理论、数据和程序。本文详细阐述了bootstrap技术的原理及其在两性生命表研究中的应用。在实际应用中，必须结合两性生命表理论，通过收集更多的生命表数据，妥善应用bootstrap技术以及TWOSEX-MSChart,TIMING-MSChart和CONSUME-MSChart等两性生命表分析软件。

生态学是一门年轻的学科，有许多悬而未决的科学问题亟待科学家解决。两性生命表理论与软件经过三十余年的研究，已逐渐成熟。然而，在实际应用上，仍有许多问题有待解决。生命表研究与多数科学试验一样，必须在可控制的条件下(温度、湿度、光周期、寄主植物)取得能反映生物种群在这些条件下的可靠、可重复的数据。由于昆虫种群在田间受环境和寄主的影响较大，使用这些在实验室控制条件下收集的生命表数据模拟野外变动条件下的种群动态时，需要考虑实验室生命表与田间生命表的差异。可以通过调节繁殖率或存活率以获得与田间种群动态最相符的模拟结果。然而，由于野外取样只能间隔数日调查一次，而且只能记录一个生命阶段和选取有限的样本数量，因此田间取样数据也不能100%反映真实的野外种群动态。虽然有许多困难，应用生命表理论来描述和预测田间种群动态是非常重要的(Chietal.,2020)。基于年龄-龄期两性生命表和多项式定理的bootstrap技术理论值得进一步关注(Dingetal.,2021;Zhaoetal.,2021)。掌握多项式定理的理论与应用知识不仅可以加深对bootstrap技术的理解，也有助于bootstrap技术在昆虫学和生态学研究中的应用。