基于可视图法的多载波生命体征监测算法

刘影，董升华

(辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105)

近年来，随着社会经济的发展和人们生活水平的提高，人们对自身身体健康的关注度也越来越高.大多数传统的生命体征监测方法需要使用接触式设备，如呼吸监测带记录器、指夹式血氧检测仪、贴片式心率仪等，这些方式需要贴身穿戴，给用户带来诸多不便.

随着无线通信技术的发展，非接触式生命体征监测技术逐渐成为研究热点.目前已有基于多普勒雷达[1]、调频连续波 (Frequency Modulated Continuous Wave,FMCW) 雷达[2-3]和超宽带雷达[4]的研究方案.但这些系统存在一系列缺点.多普勒雷达容易受到杂波噪声和多径反射的影响，而调频连续波雷达和超宽带雷达的成本相对较高，且增加了系统的硬件要求和复杂性.以上这些方式都需要持有专用的无线设备来进行检测，不方便广泛部署.

早期研究人员采用信号接收强度(Received Signal Strength,RSS)来进行呼吸监测，但是RSS 信号易受环境变化和多径效应的影响，导致RSS 信号可能会产生波动效应，引起算法监测性能的下降.与RSS 信号不同，信道状态信息(Channal State Information,CSI)是比RSS 更细粒度的信号，位于无线通信协议的物理层，可以反映小尺度衰落和微运动引起地多径效应，对环境噪声更具抗干扰性，因此CSI 在生命体征监测、动作识别[5]、跌倒检测[6]等领域得到了广泛应用.Liu等[7]第一次使用CSI振幅信息监测睡眠时的生命体征，证明了可以通过分析CSI 振幅的功率谱密度监测人的心率.Wang等[8]利用相位差消除相位偏移和噪声，从而获得更加稳定的相位信息监测生命体征.戴欢等[9]利用线性变换消除相位偏移和噪声，线性变换不仅可以消除相位偏移和噪声，还能进一步消除恒定相位误差，获得更加真实的相位波动情况以监测生命体征.张大庆等[10]将菲涅尔区理论引入基于Wi-Fi 的CSI信号的呼吸检测中，为无线感知技术研究提供了新的视角和理论依据.

文献[11-12]根据菲涅尔区衍射模型指出基于Wi-Fi 的小尺度识别活动中存在感知盲区.现有的解决方法主要有利用幅度与相位的互补性和利用多载波菲涅尔区的互补性.马程程等[13]提出利用幅度和相位的互补性解决感知盲区问题，但是相位信息由于存在相位偏移且易受噪声影响需要线性变换，这极大增加了系统的运行时间和计算量.因此探索一种单纯使用CSI 幅度信息方法对解决小尺度活动识别中的感知盲区具有重要意义.

复杂网络已经广泛应用于物理学、数学、生物学、社会学等一系列学科中，在信息传播预测[14]、大气污染物研究[15]和方位检测[16]等领域得到了广泛应用.上述的研究工作表明，将时间序列数据转换为复杂网络可以揭示数据之间的内在联系，更有效地分析数据，提高算法的性能.

综上分析，本文提出了一种基于可视图法的多载波生命体征监测算法.该算法将网络分析方法应用于基于CSI 的生命体征监测中，充分利用子载波之间的相关性，构建高感知性能的生命体征的特征模型.该算法首先采用Hampel 滤波器，滤除直流分量和异常点；然后对每个数据包所包含的子载波的CSI 数据构建一个复杂网络，利用可视图法提取出合适的网络特征参数，得到由网络特征参数构成的数据；最后对该数据进行离散小波变换提取正常呼吸和心跳频率范围内的生命体征信息，呼吸频率估计采用峰值检测算法，可以有效去除假峰并估计出的呼吸频率.而心跳频率估计采用快速傅里叶算法，在频域中通过定位峰值所对应的频率来估计心率.通过实验分析，本文所提算法与使用单个子载波或者其他算法相比具有更好的监测性能.

1 复杂网络与可视图

复杂网络是具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络.可视图(Visibility Graph,VG)作为一种构建复杂网络的新兴算法，可以有效地将时间序列数据转化为复杂网络，用来解决自然界中复杂系统的数据挖掘问题.

具体来说，首先根据时间顺序对数据进行排序，然后将每个时间点视为网络中的一个节点，根据可视性规则将各个节点进行连接组成一个复杂网络.图1（a）表示一个时间序列，将每个时间点视为网络中的一个节点，根据可视性规则将各个节点进行连接，各个节点连接完成之后组成如图1（b）的网络.可视图算法规则如下：

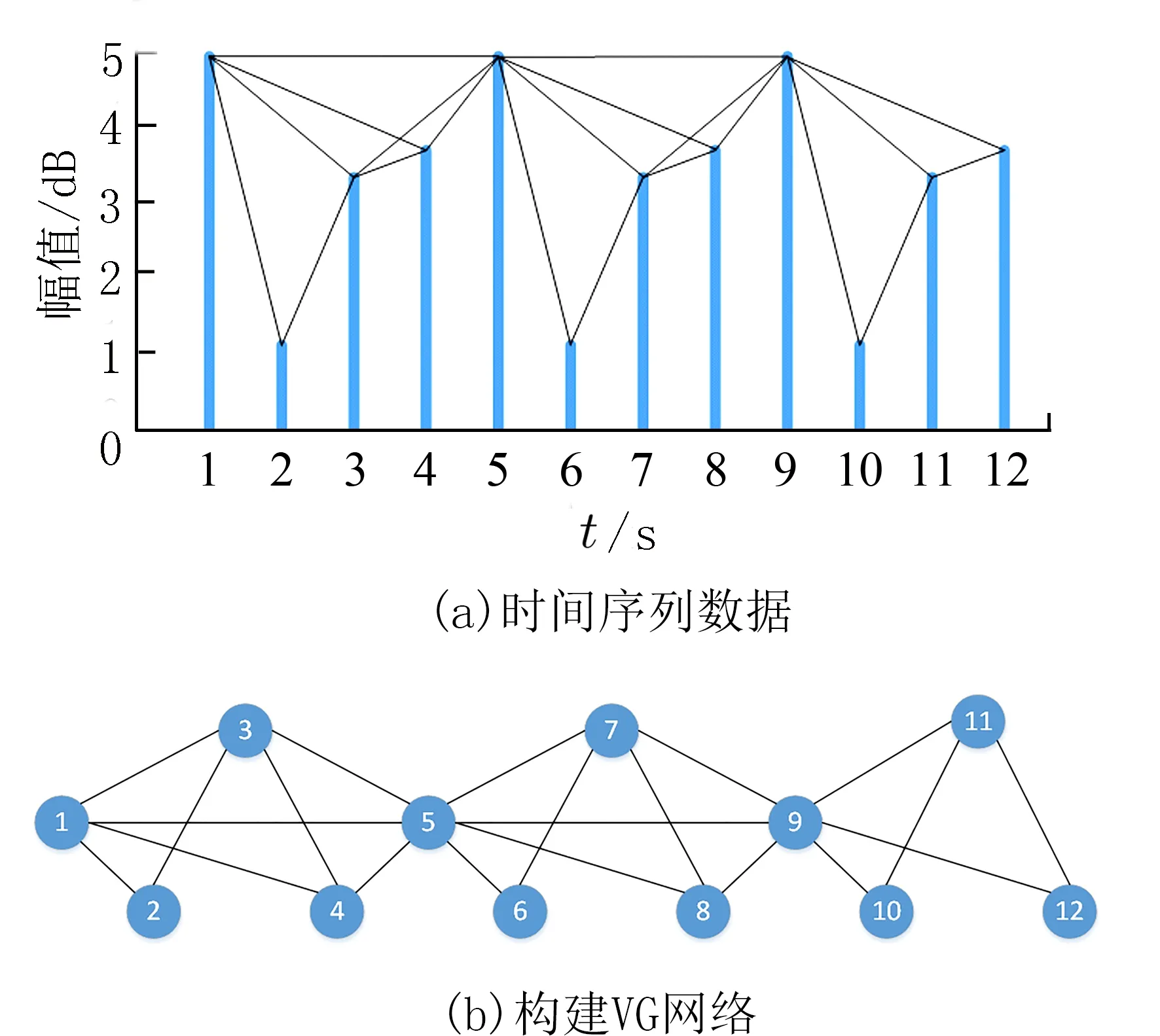
图1 VG 分析示例图Fig.1 Example of VG analysis

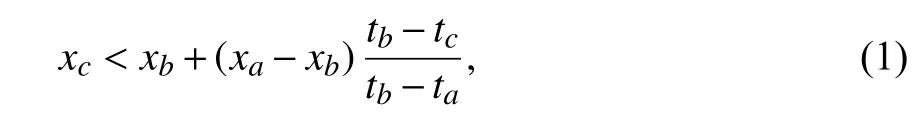
式中，a ＜ b ＜ c，如果两个节点满足上述关系，则两个节点被认为是相互可视的.换句话说，当两个节点彼此可视时，两个节点顶部的连线不与任何其他节点相交.如节点1 与节点4 顶部的连线不与其他节点相交，所以它们彼此之间是可视的，而节点2和节点4 顶部的连线与节点3 相交，这两个顶点彼此是不可视的.

2 基于VG 的生命体征监测算法

2.1 系统构架本文提出了基于VG 的多载波生命体征监测算法，利用传统的CSI 幅度数据与使用可视图法提取出的网络特征信号结合进行生命体征监测.系统架构如图2 所示，主要包括4 部分：数据采集、预处理、呼吸频率估计和心率估计.使用路由器和连着接收天线的台式机采集CSI 数据.预处理部分主要包括数据校准、可视图法提取网络特征参数和离散小波变换.呼吸频率估计部分主要有峰值检测、假峰去除.心率估计部分采用了基于快速傅里叶变换（(Fast Fourier Transform，FFT)）的方法.

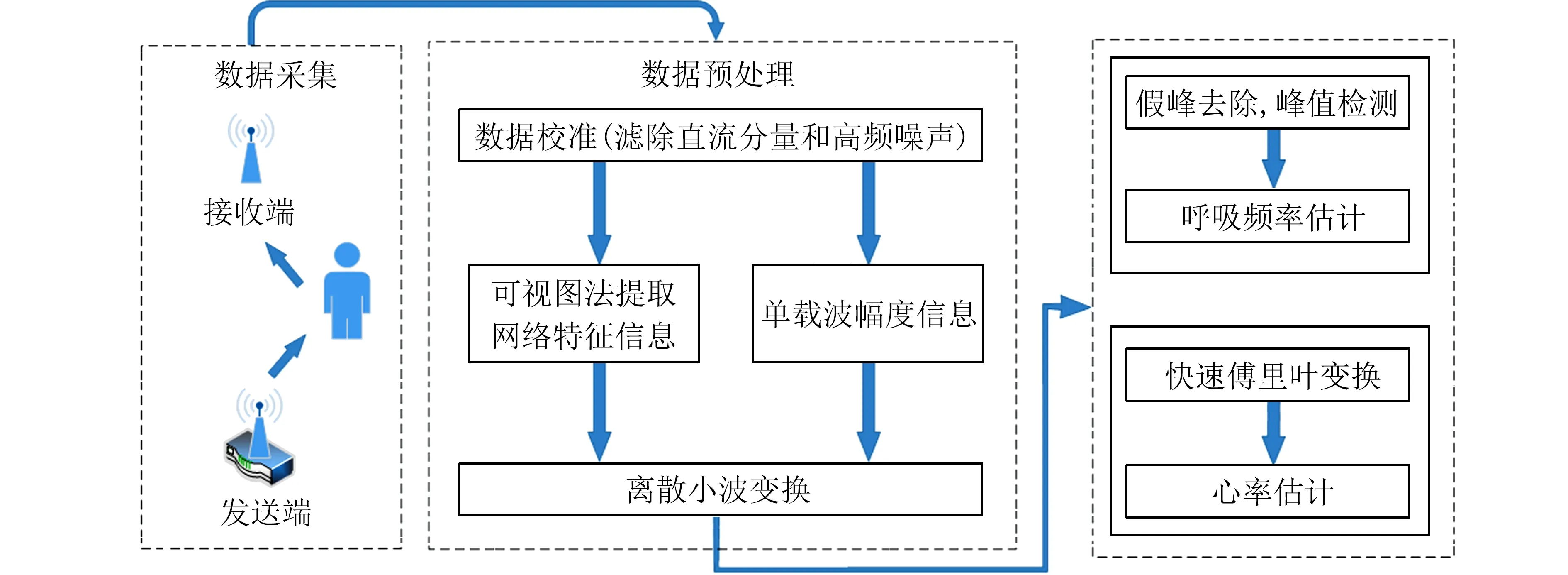
图2 生命体征监测系统流程图Fig.2 Flow chart of vital signs monitoring system

2.2 数据校准为了获得更鲁棒的CSI 数据，本文采用数据校准去除直流分量和异常点.使用Hampel 滤波去除直流分量，直流分量影响峰值检测和FFT 频率估计.与传统的仅去除高频噪声的数据校准方法不同，本文使用Hampel 滤波器对原始CSI 数据进行去趋势化.利用Hampel 滤波器获得原始数据的基本趋势，数据预处理过程如图3 所示，首先设置Hampel 滤波器的滑动窗口为1 000，阈值为0.01，得到原信号x1的基本趋势信号x2.然后从原信号中减去基本趋势信号，得到去趋势信号x3.最后，设置滑动窗口为500，阈值为3，去除异常值和高频噪声，得到去噪后的信号x4.

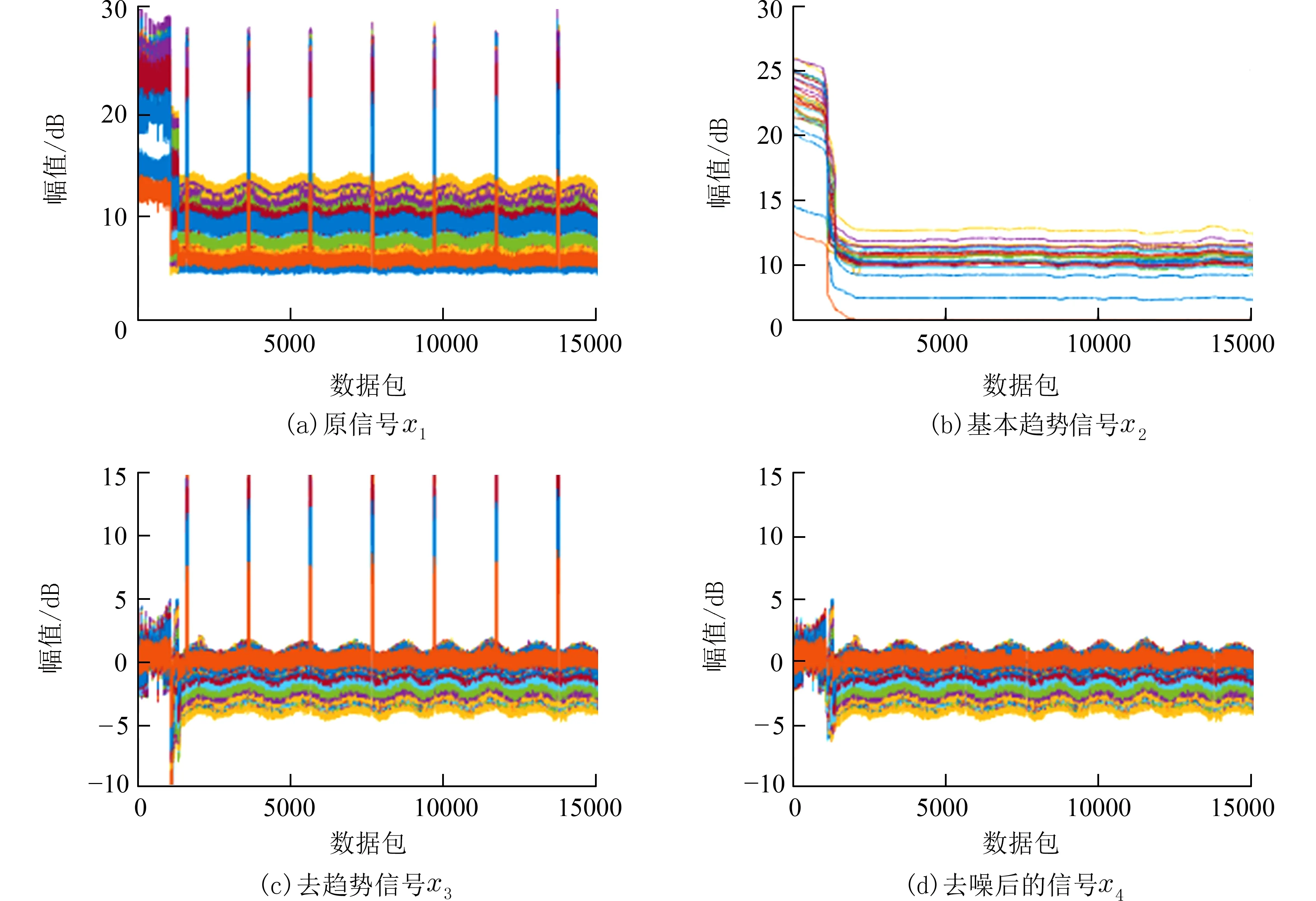
图3 数据预处理过程对比图Fig.3 Comparison chart of data preprocessing process

2.3 可视图法提取网络特征参数

2.3.1 算法原理 为了构建VG 算法需要的时间序列，本文将收集到的CSI 信息从时域扩展到频域，对子载波的中心频率进行排序，将排序后的频率作为VG 的时间序列，然后将可视图法应用于已排序的子载波.因此，本文研究的是相邻子载波之间的相关性，而不是时间序列的相关性.如图4（a）所示的30 个子载波.每个子载波对应于网络中的一个节点.根据可视性规则将这些节点进行连接，得到一个复杂的网络.如图4（b）所示.

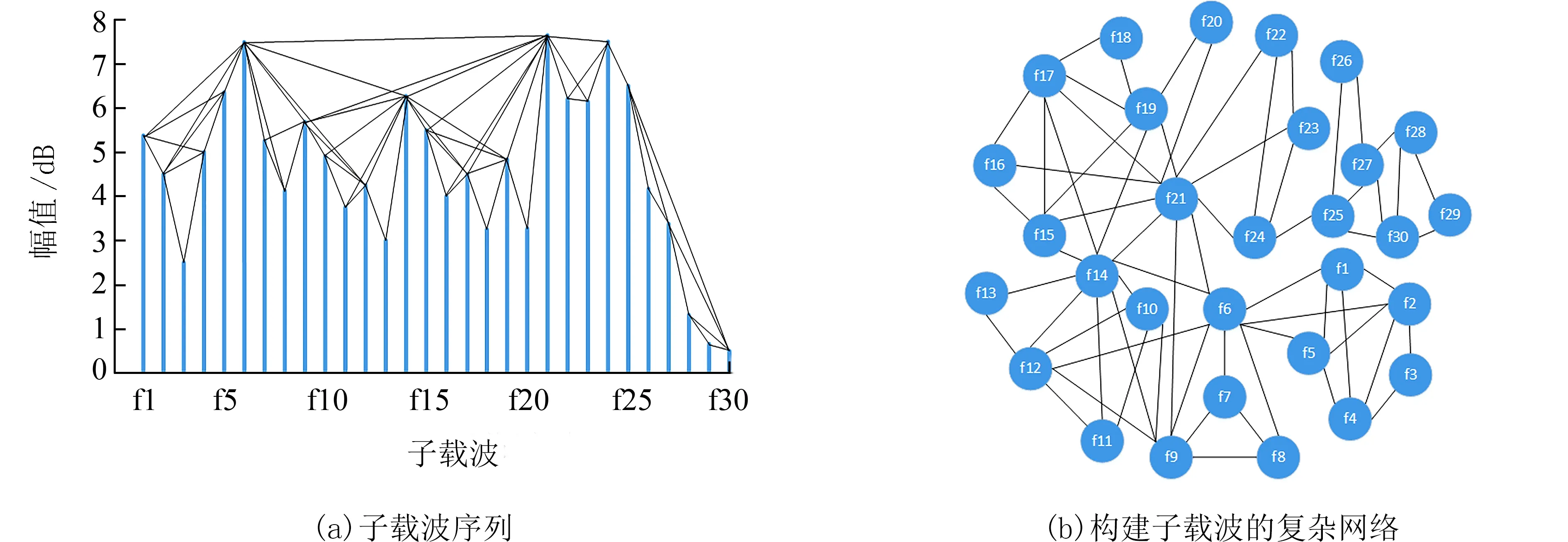
图4 CSI 数据的VG 分析示例Fig.4 Example of VG analysis for CSI data

在基于VG 得出复杂网络后，需要提取出具有代表性的网络参数，本文选取平均聚类系数作为网络参数.聚类系数的定义如下所示：

式中，Ci是节点i的聚类系数，τi,Δ是以节点i为中心的闭合三元组的数量，τi是网络中三元组的总数.因此，平均聚类系数的定义为：

式中，N是网络中的节点总数.在提取出每个数据包的网络参数后，得到一个有网络参数构成的信号.

2.3.2 算法优势 由于呼吸和心跳活动的幅度往往只有毫米级或厘米级，无法穿越一个完整的菲涅尔区，使得接收到信号的波形只是一个片段，该信号的模式与被感知目标所处的位置有关.如图5所示，被感知目标在位置a、b、c、d 处运动时，波动模式是不同的，在位置a、c 对应的片段信号波动大，而位置b、d 对应的片段信号波动小而容易被噪声淹没，因此位置b、d 既菲涅尔边界处为生命体征监测的感知盲区.

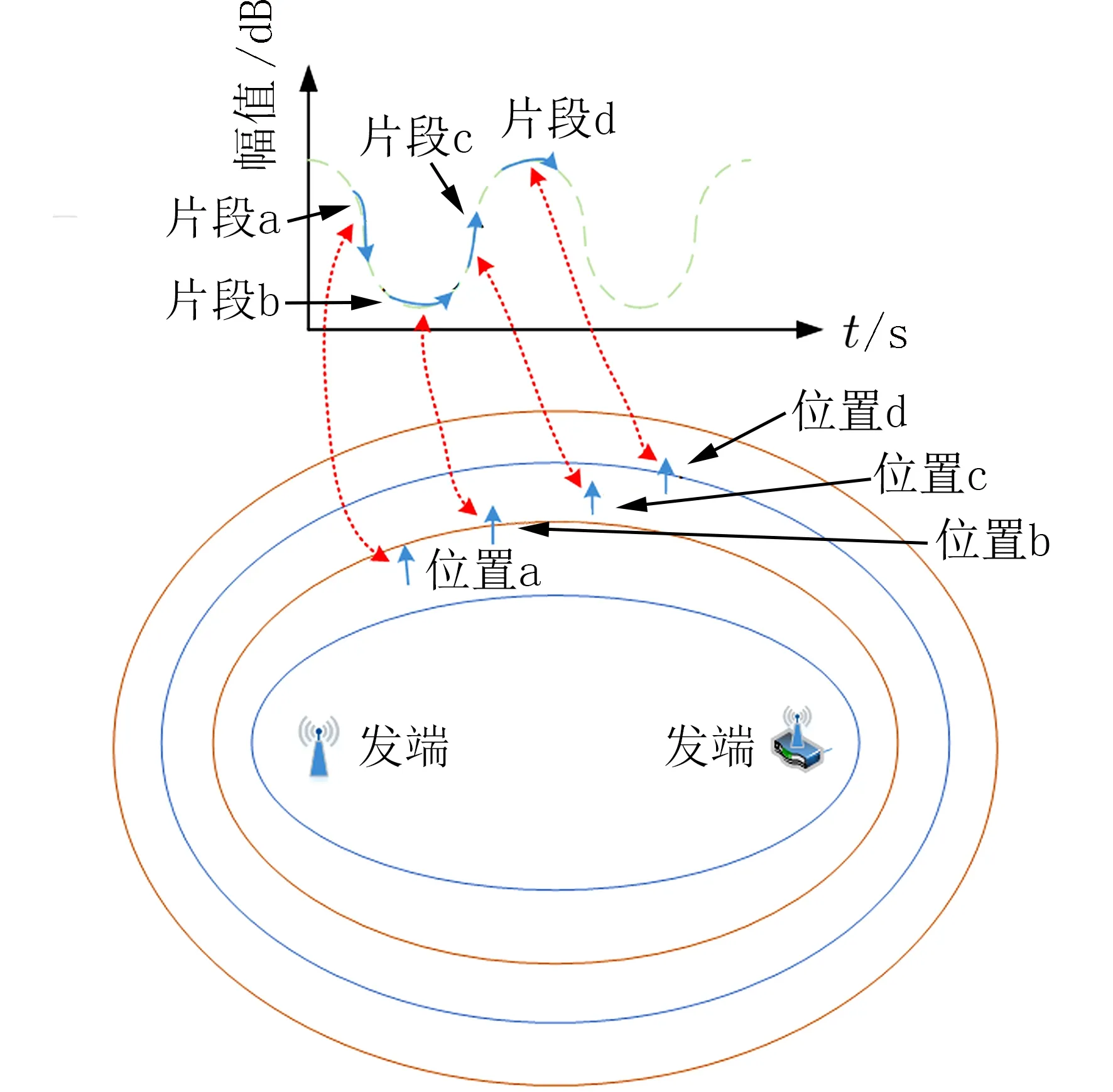
图5 感知盲区Fig.5 Perception of blind area

不同的子载波的中心频率是不同的，从而导致所对应的波长会有稍微不同，由菲涅尔半径公式可知波长λ会影响菲涅尔半径的大小，所以不同子载波的菲涅尔半径的大小也会有稍微不同.载波中心频率相差越大，所对应的菲涅尔半径相差也就越大，菲涅尔半径计算公式如下：

式中，k为菲涅尔区序号，d1、d2分别为发射端和接收端到视距路径中点的距离，λ为载波中心频率对应的波长.

如图6 所示，当感知目标位于一个菲涅尔区的感知盲区时，可能位于另一个子载波的非感知盲区.因此可以利用多载波菲涅尔区解决感知盲区问题.目前基于802.11n 协议的Wi-Fi 技术使用了56个子载波，而我们利用Daniel Halperin 提供的CSITools 工具软件只可以获取其中的30 个子载波.由式(4)可知载波中心频率相差越大，菲涅尔半径相差也就越大.为了尽可能地使感知目标位于某一菲涅尔区的非感知盲区，本文利用了可以获取到的30 个子载波之间的相关性进行建模，所提取出的网络参数包含了30 个子载波的信息，可以有效解决由于菲涅尔相位的存在导致的单个子载波存在感知盲区问题.

图6 多载波菲涅尔区Fig.6 Multicarrier wave Fresnel region

采用幅度与相位结合[17]的方法虽然可以有效避免位置依赖性和感知盲区问题，但CSI 相位信息存在相位偏移，且易受到环境中的噪声影响，现有的解决方法主要有相位差和线性变换.然而，相位差只能去除相位的定时偏移和噪声，无法去除恒定相位误差[13].线性变换虽然可以去除恒定相位误差，但是极大地增加了系统的运行时间和计算量.

2.4 基于离散小波变换的生命体征信息提取通过2.3 节方法得到去除了噪声和异常点的时域信号，接下来利用离散小波变换(Discrete Wavelet Transform,DWT)提取出正常呼吸和心跳频率范围内的信号.DWT 可以实现数据的时-频域表示，不仅可以在时域和频域提供最佳分辨率，而且可以对数据进行多尺度分析.使用DWT 后的数据可以分解为不同尺度下的近似系数分量和细节系数分量，如图7 所示.

图7 离散小波变换结果图Fig.7 Result graph of discrete wavelet transform

由于呼吸和心跳都属于小尺度运动，易受环境噪声干扰，较低的采样频率并不能有效地监测呼吸和心跳，因此本文根据呼吸和心跳的频率特点选择采样频率为480 Hz，进行9 次离散小波变换后，细节系数d8 的频率范围为0.937 5～1.875 Hz，近似系数a9 的频率范围为0～0.468 75 Hz.由于正常人的呼吸频率范围为0.2～0.4 Hz，心率范围为1～1.66 Hz，所以本文使用细节系数d8 表征心跳信息，近似系数a9 表征呼吸信息.提取出呼吸和心跳信号后，根据它们的特点分别使用不用的方法进行估计，由于使用FFT 的方法估计呼吸频率的精度不高，而心跳信号的小峰值几乎不可见，使用峰值检测的方法无法有效提取出心跳信号.所以本文使用峰值检测的方法估计呼吸频率，使用FFT 的方法估计心率.

2.5 呼吸频率估计正常人的呼吸频率范围为0.2～0.4 Hz，所以本文对离散小波变换后近似系数分量a9 进行峰值检测，对所有峰-峰间隔进行平均，得到平均呼吸周期，最后求出呼吸频率.

在峰值检测过程中会出现很多假峰.为了滤除假峰.本文根据最小呼吸周期原则检测每个峰的半宽以去除假峰.如图8 所示，具体来说，人的呼吸范围为10～37 次/min，以最大呼吸频率对应的最小呼吸周期t作为阈值，当峰的半宽小于t/2时，就被判定为假峰.t的计算公式可表示为：

式中，f为信号采样频率.如图8 中P2、P4 的半宽小于所设定的阈值，所以被判定为假峰.而P1、P3、P5、P6、P7、P8 等的半宽大于阈值t，被判定为真峰.

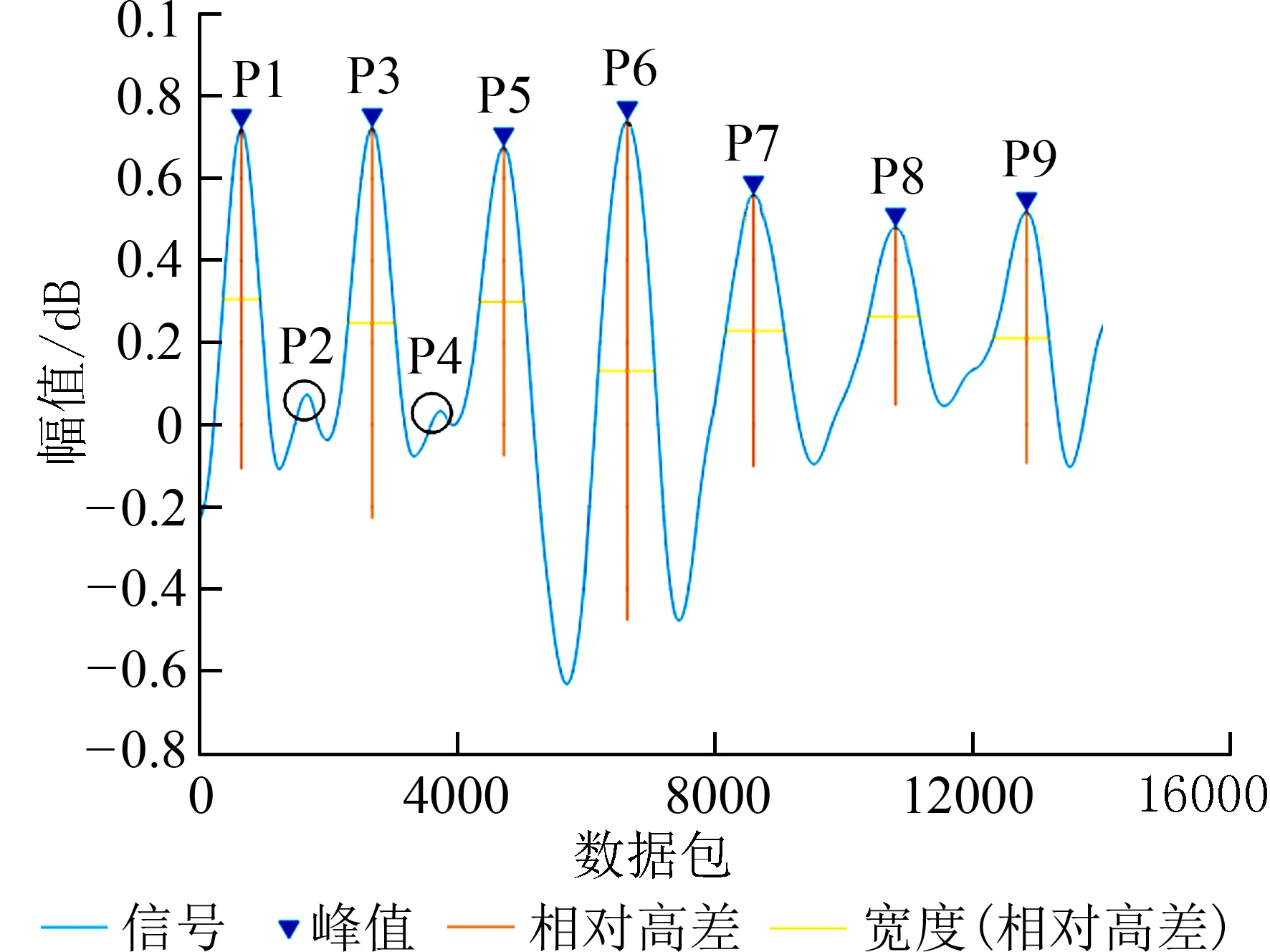
图8 峰值检测后的呼吸信号Fig.8 Respiratory signal after peak detection

2.6 心率估计正常人的心率范围为1～1.66 Hz.本文对离散小波变换后的细节系数d8(0.937 5～1.875 Hz)进行FFT 变换，然后找出频率范围内最大的峰值，该峰值对应的频率即为心跳频率，如图9 中的心率估计为1.244 Hz.

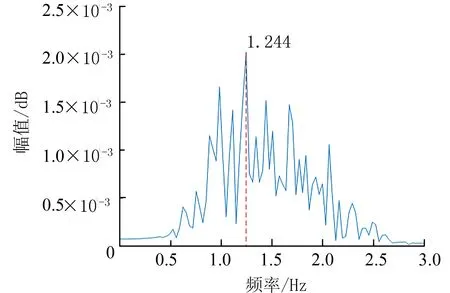
图9 基于FFT 算法的心率估计Fig.9 Heart rate estimation based on FFT algorithm

3 实验及分析

3.1 实验设置实验阶段，使用连接着3 根全向接收天线的台式机作为接收端，台式机配备有Intel 5300 网卡和开源工具CSI-Tools[18]，发送端使用商用TP-Link 无线路由器，实验环境如图10 所示，在不同环境(走廊、实验室和会议室)、不同收发距离与不同人体姿态等条件下进行对比实验，实验由3 名志愿者在一个月内完成，采样率设置为480 Hz，使用医用多参数监护仪记录心率和呼吸的真实值.

3.2 结果及分析

3.2.1 评价指标 本文采用错误率[19]衡量算法的性能，错误率是使用最广泛的分类指标，其计算的公式为：

3.2.2 参数设置

3.2.2.1 不同天线的影响 接收端采用的是3 根全向接收天线，由于接收设备的差异和摆放位置的不同，不同的天线对呼吸和心跳信号的敏感度不同，本文根据不同天线的平均方差的大小选择合适的天线.选择平均方差最大的天线.本文中，选择第三根接收天线.图11 为在实验室环境下，收发距离为1 m，坐在视距路径中间时不同天线的监测结果，所选天线的错误率最低，证明了本文所选择天线的方法的合理性.

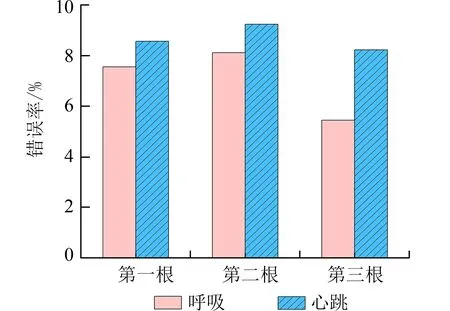
图11 不同接收天线的监测性能Fig.11 Monitoring performance of different receiving antennas

3.2.2.2 不同小波函数的影响 在使用离散小波变换时，需要选择合适的小波函数.图12 显示了在实验室环境下，收发距离为1 m，坐在视距路径中间时不同的小波函数对检测性能的影响.我们发现当采用小波函数db1、db2、db3 时的平均错误率较高，这说明这些小波函数不适合用来进行呼吸心跳信号的分解.而采用db4、db5、db8、db9 时的平均错误率比较低，其中采用db8 时的平均错误率最低.因此，本文采用小波函数db8 来进行离散小波变换.

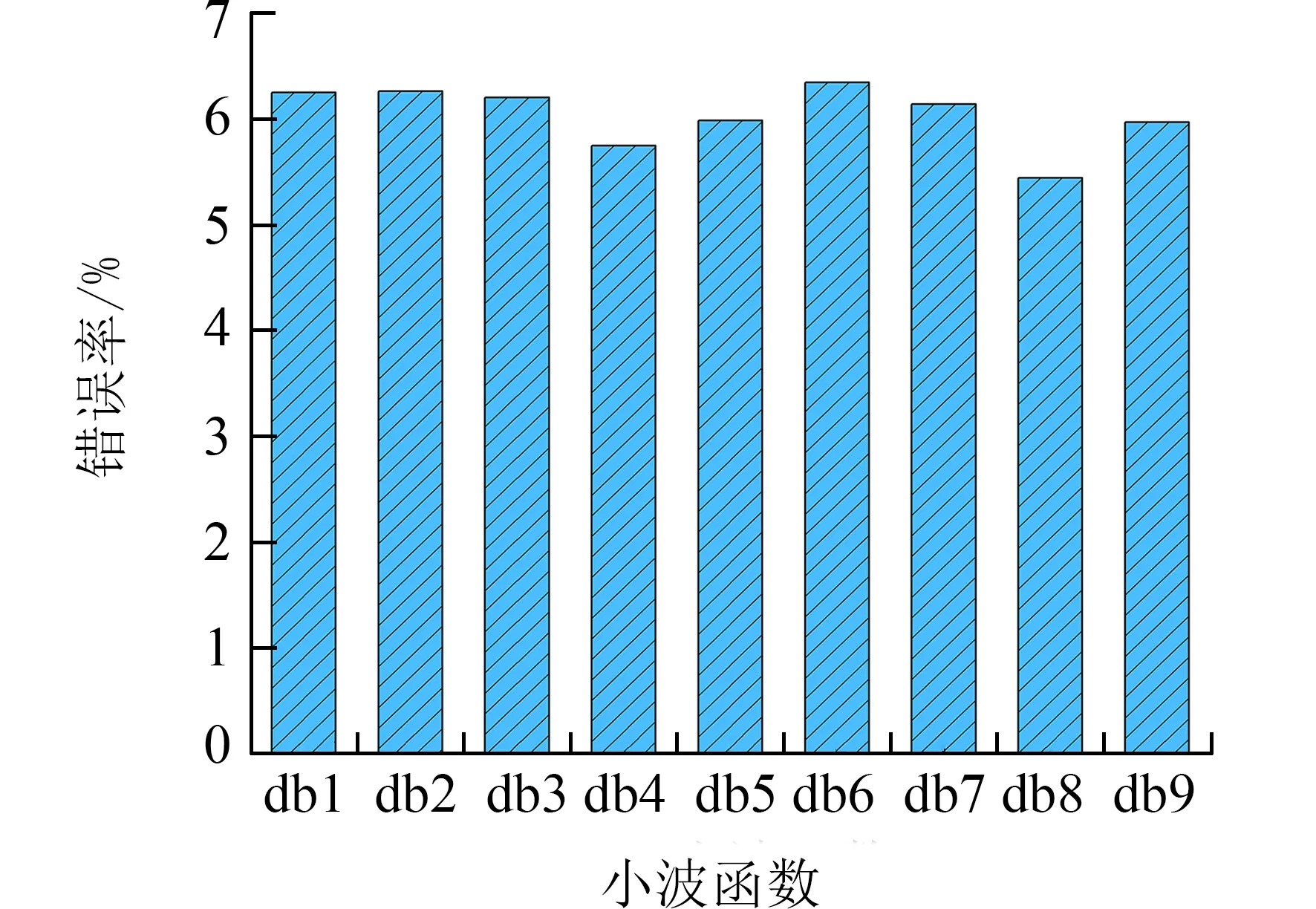
图12 不同小波函数的监测性能Fig.12 Monitoring performance of different wavelet functions

3.2.3 算法性能分析

3.2.3.1 呼吸 为了验证本文算法的性能，实验过程中，收发距离为1 m，测试人员坐在胸腔距离地面1 m处，分别在垂直距离视距路径中点0.5 m和1 m 位置分别进行多次实验.其中呼吸监测的性能如图13 所示.

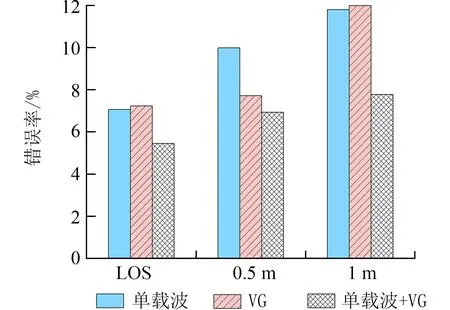
图13 呼吸频率估计性能分析Fig.13 Analysis of breathing rate estimation performance

从图13 可以看出，随着距离的增加，错误率会上升.而本文方法的监测性能仍然优于仅使用VG的方法和使用单个子载波的方法.如在垂直距离LOS 路径中点0.5 m处，使用单个子载波的方法的呼吸频率平均错误率为9.98%，使用VG 的方法的呼吸频率平均错误率为7.71%，使用单子载波加VG 的方法的呼吸频率平均错误率为6.92%，比使用单个子载波的方法错误率降低了3.06%.

3.2.3.2 心跳 心率检测的性能如图14 所示.本文算法的性能与仅使用VG 的方法和使用单个子载波的方法相比更加稳定和优异.如在垂直距离视距路径(Line Of Sight，LOS)路径中点1 m处，使用单个子载波的方法的心率平均错误率为11.66%，使用VG 的方法的心率平均错误率为10.48%，使用单子载波加VG 的方法的心率平均错误率为9.4%，比使用单个子载波的方法错误率降低了2.26%.

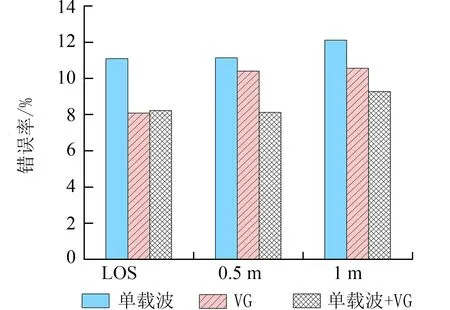
图14 心率估计性能分析Fig.14 Analysis of heart rate estimation performance

3.2.3.3 不同收发距离对算法性能的影响 图15显示了在大教室的环境中，人坐在视距路径中间，不同收发距离（1、2、3、4、5 m）下的呼吸频率和心率的错误率.由图15 可知，随着收发距离的不断增加，平均错误率也在不断增加.其中呼吸的平均错误率由5.44%上升到10.85%，而心率平均错误率由8.22%上升到11.67%.这是因为随着收发距离的增加，反射信号会减弱，从而影响了监测的性能.

图15 不同收发距离对实验的影响Fig.15 The influence of different distance between the transmitter and receiver on experiment

3.2.3.4 不同场景对算法性能的影响 图16 显示了在不同的环境中，收发距离为1 m，人坐在视距路径中下的呼吸频率和心率的错误率.根据测试结果可以看出，在走廊的环境下，由于多径效应且反射路径复杂，对信号的干扰也就较大，导致监测性能较差.而在小教室和实验室中相对比较空旷，监测性能较好.

图16 不同环境对实验的影响Fig.16 The influence of different environment on the experiment

3.2.3.5 不同测试方位对算法性能的影响 图17显示在大教室环境中不同的测试姿势对测试性能的影响.我们考虑3 种典型常见的姿势，坐着、站着和躺着.实验过程中，测试人员位于视距路径中间，收发距离为1 m.结果如图17 显示，站着的时候，呼吸和心跳平均错误率相比于坐着和躺着的时候，平均错误率更高.这是因为当人站立的时候身体会出现抖动，而且胸部对信号的反射相对较弱.

图17 不同姿势对实验的影响Fig.17 The influence of different posture on the experiment

3.3 本文方法与幅度相位结合方法的比较通过2.3.2 节分析可知，目前针对感知盲区的解决方法主要有利用幅度与相位的互补性和利用多载波菲涅尔区的互补性，本文提出的利用可视图法的多载波生命体征检测算法利用了多载波菲涅尔区的互补性，在实验室环境下，坐在距离LOS 路径中点1 m处采集30 次数据，每次数据时长30 s，对两种解决方法的性能进行对比，结果如表1 所示.

表1 两种解决方法错误率和运行时间比较Tab.1 Comparison of error rate and running time of the two solutions

虽然本文方法的心率错误率略高于采用幅度于相位结合的方法，但是呼吸率错误率低于幅度于相位结合的方法，且每次的运行时间不到幅度与相位结合方法的一半.

3.4 不同文献算法的比较基于上述实验，利用本文的实验环境下采集的数据，将本文所提算法与使用CSI 幅度的算法[8]MVSP、使用CSI 相位的算法[11]VSMPC 和使用相位差的算法Phase Beat[10]进行比较.呼吸频率估计误差的累计分布函数（Cumulative Distribution Function，CDF）结果如图18（a）所示，本文算法91%的测试数据的估计误差小于3 beat/min，MVSP、VSMPC 和Phase Beat 分别有64%、60%和66%的测试数据的估计误差小于3 beat/min.心率估计误差的累计分布函数如图18（b）所示，本文算法92%的测试数据的估计误差小于3 beat/min，MVSP 和VSMPC 分别有90%、76%和76%的测试数据的估计误差小于15 beat/min.本文算法在呼吸频率估计和心率估计中的性能都优于MVSP、VSMPC 和Phase Beat.

图18 不同算法估计误差对比Fig.18 Comparison of estimation errors between different algorithms

4 结束语

本文提出了一种基于VG 的多载波生命体征监测算法，解决了使用单个子载波的幅度或相位信息进行生命体征监测时存在感知盲区问题.该算法利用子载波之间的相关性进行建模，利用可视图法构建子载间高感知性能的复杂网络，采用网络分析方法提取出网络特征参数，并设计用于表示、构造多载波信息的网络特征信息.在不同环境、不同收发距离、不同人体姿态等条件下进行大量实验，实验结果表明，本文所提算法能够有效监测人体生命体征，与传统的采用单子载波方法相比错误率降低了3%左右，具有更好的检测性能.此外，本文主要针对单人的呼吸和心跳频率进行监测，后续的工作将研究在多人的情况下进行生命体征监测.