基于自适应欠阻尼系统随机共振方法的故障诊断
任韵君,张建刚
(兰州交通大学 数理学院,甘肃 兰州 730070)
旋转机械是大型机械设备中最常见的设备,这些机械设备的关键部分都是滚动轴承,其包括转子系统、轴承系统等,由轴承故障引起的严重事故不在少数,带来的损失巨大,因此对于轴承的故障检测尤为重要.随着信号理论的发展,用于检测初期轴承故障的方法主要有小波变换(Wavelet Transform,WT)[1]、经典模态分解(Empirical Mode Decomposition,EMD)[2]、集成经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)[3],以及随机共振(Stochastic Resonance,SR)等,其中基于SR的故障诊断是利用噪声对故障产生的微弱信号进行增强,这促使人们对噪声的作用及影响进行重新认识和研究.
SR 最早是在研究古气象学周期性递归的过程中发现和提出的[4-5].研究发现噪声不仅不会破坏原有的系统,反而可以加强系统的响应.在发现这一现象后人们广泛地将SR 应用到故障诊断中.首先根据势函数的不同产生SR 效应的强度也不同,已有经典双稳态势(Conventional Potential Stochastic Resonance,CBSR)[6]、单稳态势(Gaussian Potential Stochastic Resonance,GP)[7]、Woods-Saxon(Woods-Saxon Potential Stochastic Resonance,WS)势[8]、周期势[9]、三稳态势[10]、时延势(Time-delayed Feedback Stochastic Resonance,TFSR)[11]等;其次优先考虑了过阻尼系统;之后多项研究[12-13]表明,欠阻尼系统的阻尼因子也会影响粒子跃迁的效率[14],最终影响SR 性能,据此进一步研究了欠阻尼系统.
1964年,FitzHugh 和Nagumo 将H-H神经元模型[15]简化为了二维非线性模型FitzHugh-Nagumo,称为FHN 模型[16],FHN 模型以更简洁的方式描述神经元释放到细胞膜中的节律.研究结果表明大多数生物神经系统具有敏感的弱信号感知能力,并且欠阻尼系统具有二次滤波功能,故本文将研究欠阻尼FHN 系统与其系统参数的关系,并将结论用于弱信号检测中.本文提出了一种基于FitzHugh-Nagumo 势的自适应双稳态SR 的故障诊断方法(AUFHNSR),该方法可以通过选择合适的参数起到增强弱信号的功能,进而将弱信号提取出来,得到最优输出.
1 欠阻尼FitzHugh-Nagumo 随机共振系统
1.1 数学模型为了得到更佳的微弱故障的检测效果,本文提出了一种基于FHN 势的欠阻尼方法.该方法的二阶系统的 L angevin方程[17]可以描述为:

式中,x(t)表示系统的输出信号,在实际应用中对应于经过随机共振方法诊断后的输出信号;s(t)=Acos(2πft+φ)是周期信号即模拟轴承周期性地滚过故障产生的信号,A代表幅值,f为驱动频率,φ为相位,令ω=2πft;(t)模拟的是覆盖故障信号的强噪声,满足〈N(t)〉=0,〈N(t)N(t′)〉=2Dδ(t-t′)的性质,D表示噪声强度,ξ(t)为高斯白噪声[17];U(x)是非线性双稳态势,配合周期信号s(t)和噪声N(t)产生随机共振现象.一般工程信号对应的参数较大,本节只针对小参数进行理论讨论.双势阱U(x)的表达式表达如下:

将(2)式代入(1)式中得到:

式(5)对应的系统模型如图1 所示.


图1 基于FitzHugh-Nagumo 势的自适应双稳态SR方法的系统模型Fig.1 System model for adaptive bistable SR method based on FitzHugh-Nagumo potential

粒子运动的概率密度p(x,y,t)通过FPK 方程来推导[17],表达式如下:

根据双稳态理论[20]和两态模型[21]理论,布朗粒子在势阱之间的跃迁速率可表示为:

在绝热近似[17]条件下,忽略A的二次项,得到系统的输出信噪比(Signal-to-Noise Ratio,SNR)为:

由以上的推导可以看出输出信噪比与系统参数有关,图2(a)~(c)为(11)式表示的信噪比分别与阻尼因子 γ、参数a、参数b的关系图,其中噪声强度D从0 增加到2,对应的参数为a=2.01,b=0.25,γ=0.8.可以看出,信噪比随系统参数表现出了显著的非单调特性.从另一个方面也可以说,通过选择合适的参数,AUFHNSR 系统的输出信噪比可以优化.

图2 信噪比与参数的关系图Fig.2 Plot of signal-to-noise ratio versus parameters
2 数值模拟与轴承故障诊断
2.1 基于FHN 系统的工程信号处理上节理论分析了AUFHNSR 系统,但所有推导都局限于小参数限制,而实际的工程信号不满足小参数限制,在这种情况下无法得到解析的随机共振解,且在离散时间系统中处理数字信号有更多的优势.因此本文采用四阶Runge-Kutta 数值模拟的方法确定欠阻尼系统的数值模拟解,进而进行故障诊断.
从表1可以看出,广西金融术语的翻译过于放在字面的翻译,而忽略了实际的意义体现。但是,纵观后期的金融翻译,广西金融翻译也出现了采用香港金融翻译的现象。[4]
通过傅里叶变换计算x[n]的功率谱,即可得到系统对应的输出信噪比[21]表达式为:

式中,Es(f)和En(f)分 别表示特征频率f处的功率和信号特征频率f周围噪声的平均功率,其中表示信号的长度.输出信噪比越大,表明对信号特征的提取效能越好.结合1.2节输出信噪比与系统参数和阻尼因子的关系,此处引入量子粒子群优化算法(Quantum Particle Swarm Optimization,QPSO)[22]对系统参数等进行优化.QPSO 算法是建立在粒子群算法(Particle Swarm Optimization,PSO)算法的基础上,以粒子群的位置即需要优化的参数作为决策变量,搜索最好的适应值即以(12)式定义的离散系统的输出信噪比为寻优指标.当粒子处于某一位置时,输出此位置对应的系统进行随机共振处理后的序列,进一步根据(12)式计算其对应的适应值.最终输出当适应值最大时对应的粒子群的位置,则该位置即为本文系统对信号特征提取效能最好时对应的最优参数.综上,AUFHNSR 方法的流程描述如下:
步骤1信号预处理.运用包络提取即用希尔伯特变换解调得到包络信号为信号的预处理.
步骤2参数初始化.设置参数a,b,γ的取值范围即寻优范围及迭代次数.
步骤3参数优化.使用QPSO 算法[22]对系统中的参数进行优化,取h=0.000 1,将式(12)得到的信噪比作为QPSO 算法的寻优指标,寻找最大输出信噪比时对应的匹配参数.
步骤4应用到弱信号检测.将最优参数代入原系统,再将第(1)步得到的预处理信号作为新系统的输入信号,然后采集最优输出波形作为检测信号,计算出相应的功率谱用于目标信号识别.
2.2 模拟信号的故障诊断根据1.1 节中(1)式对轴承故障信号s(t)的 定义,且s(t)会随着运行条件的不稳定导致不均匀的脉冲,故我们选择单边衰减脉冲函数作为模拟故障信号,即:
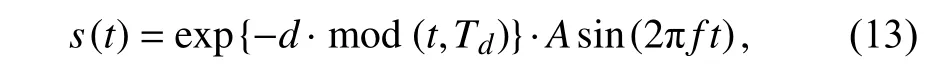
式中,A为信号的幅值,f为载波频率,d反映了衰减速率,n(t)=[t/Td]控 制脉冲的周期,Td=1/fd是脉冲区间(fd是驱动频率).此处相应的参数取值分别为:f=2 000 Hz,A=1,fd=100,d=30 000.加 高斯白噪声N(t)为 噪声强度D=0.5的噪声信号,产生于轴承运行过程中其余部件之间的摩擦等.对于欠阻尼FHN 系统,使用QPSO 算法求得的最优参数为a=2.493 7,b=0.112 7,γ=0.107 6.
图3(a)所示为单边衰减脉冲函数s(t)的时域和频谱.图3(b)为将噪声信号N(t)加 到s(t)后的时域波形和功率谱,可以看出图3(b)中所待测的分量被噪声完全掩盖,不能识别.图3(c)为将含噪信号经过Hilbert 变换得到的包络信号,由图可知经过包络解调后,可以指出故障的特征频率,但同时也会存在不可忽略的干扰成分导致检测错误.图3(d)为将通过包络解调后的信号作为欠阻尼FHN 系统的输入进行故障诊断即AUFHNSR 方法时,得到的输出信号的时域波形和频谱图,由图3(d)可以看出原本的噪声干扰基本消除,从功率谱来看,待测频率在100 Hz 处得到了显著的提高,待测分量得到显著提升.

图3 采用不同方法分析单边衰减脉冲的结果Fig.3 The results of unilateral decaying pulses analyzed using different methods
2.3 实验验证为了检验AUFHNSR 在实际应用中的价值和有效性,本节对来自两个不同实验室的故障轴承数据进行了测试.
2.3.1 数据1 首先使用的信号取自Case Western Reserve University (CWRU)的电气工程实验室缺陷轴承数据中心的实验装置.该实验装置的驱动端轴承的采样频率为1 2 000 Hz,轴承型号为6205-2RS轴承,其滚子数量为9个,轴承中径为 39.04 mm,滚子直径为 7.94 mm,接触角为 0°.根据轴承类型和转速以及公式(14)和(15),可以求得内外圈故障的特征频率[23]相关参数分别为:内圈故障频率fBPFI155 Hz,外圈故障频率fBPFO105 Hz.
内圈故障特征频率[24]:

外圈故障特征频率[25]:
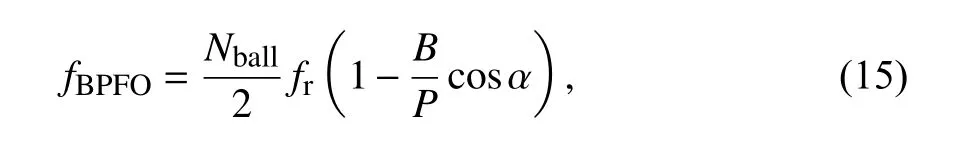
式中,fr表示电机频率,Nball表示滚子数量,B、P、α分别表示滚子直径、轴承中径和接触角.
首先对内圈故障信号进行分析.采集信号的时域和频谱如图4(a)所示,从波形中几乎找不到内圈故障脉冲,反而存在很多比故障特征更高的尖峰,使得诊断结果存在错误,无法进行故障分析与判断.图4(b)为原信号经过包络分析后的结果,从图中可以看出,功率谱中可以找出fBPFI,但是在fBPFI附近仍然存在一些噪声分量且计算对应的信噪比为28.235.采用传统SCSR[25]方法输出结果如图4(c)所示.采用本文提出的AUFHNSR 方法结果如图4(d)所示.输出波形中故障触发的脉冲可以清晰地识别出来,且大多数噪声成分被抑制.

图4 不同方法分析内圈故障信号的结果Fig.4 Results of analyzing the inner ring fault signal with different methods
其次,为了进一步验证所提方法的有效性,对外圈缺陷信号进行如下处理:图5(a)~(d)依次为原始信号、包络信号、使用传统SCSR 的输出以及本文提出AUFHNSR 的输出对应的时域图和频域图.可以看到从原始信号中不能检测出故障,包络解调后可以在功率谱中指出外滚道的故障特征频率fBPFO,同时噪声干扰也很明显.最后,使用本文提出的AUFHNSR 方法可以很明显地从功率谱中看出高频和低频噪声都得到了抑制,且低频信号抑制效果更为明显,即可以清晰地在功率谱中指出外滚道故障的频率fBPFO,同时fBPFO占主导地位,且效果略优于传统SCSR 方法.

图5 不同方法分析外圈故障信号的结果Fig.5 The results of analyzing the outer ring fault signal with different methods
2.3.2 数据2 我们选用的第二组数据来自于美国-机械故障预防技术协会(MFPT)[26]轴承故障诊断合集.此处实验用的是NICE 轴承,轴承直径为0.235,节圆直径为1.245,滚动体数量为8个,接触角为0°,驱动端轴承的采样频率为48 828 Hz,这里只分析内圈故障,输入轴转速为25 r/s,由公式(14)可以计算得到内圈故障的特征频率为118 Hz.
图6 为对MFPT 的采样数据以及数据进行处理后的时域和频域图.图6(a)为采集到的原始信号的信息,轴承故障产生的信号被噪声完全淹没故无法进行识别;图6(b)为包络信号,同样的,包络信号虽然可以指出故障特征频率,但是存在的干扰信号还是很多;图6(c)为使用传统SCSR 方法进行处理后得到的诊断结果;图6(d)为用本文提出的AUFHNSR 进行诊断的结果.可以看出传统SCSR与AUFHNSR 都可以进行故障诊断,计算对应的信噪比分别为45.287 1 和47.075 4,即AUFHNSR 优于传统SCSR.
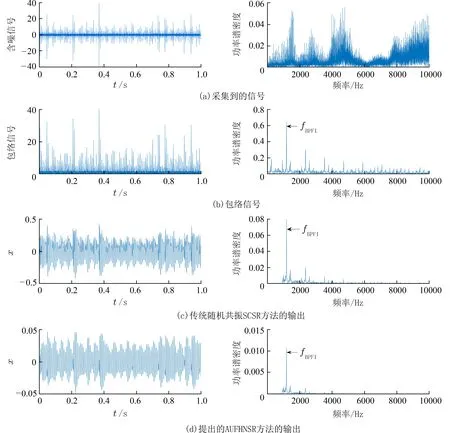
图6 不同方法分析MFPT 内圈故障信号的结果Fig.6 The results of analyzing the fault signal of the inner ring of the MFPT by different methods
2.4 实验结果总结与讨论为了定量分析,表1列出用不同故障诊断方法的输出信噪比.对比结果表明,使用AUFHNSR 方法处理的故障信号输出信噪比略高于使用SCSR 方法和包络方法进行故障诊断的结果.结合2.3 节中的滤波效果对比可以得出结论,即该方法在实际的故障检测中存在一定的优势.

表1 采用不同方法处理轴承故障信号的输出信噪比Tab.1 The output signal-to-noise ratio of using different methods to deal with bearing fault signals
3 结论
本文首先根据小参数扩展以及双稳态理论推导了基于欠阻尼FitzHugh-Nagumo 势的输出信噪比的形式,其次根据两态模型理论推导出了信噪比的解析式,根据解析式进一步的验证了信噪比会随参数及欠阻尼阻尼因子的变化而改变的结论.之后将该结论应用到故障诊断中,即提出了一种基于欠阻尼FitzHugh-Nagumo 势的自适应双稳态SR 方法(AUFHNSR),该方法是通过量子粒子群优化(QPSO)算法选择较优的系统参数和欠阻尼阻尼因子得到最优系统进而对故障信号进行检测.通过仿真和对两组实际的数据进行故障诊断及分析,对新提出方法的可行性和优越性进行了证明.未来将会使用更优越的优化算法去匹配本文系统的参数以达到更好的共振效果,同时也要考虑时滞等因素,从更实际的场景和角度出发以完善本文提出的方法.

