Kirchhoff 型分数阶Hamiltonian 系统基态解的存在性和集中性

薛婷婷，曹虹，姜永胜，刘元彬

(新疆工程学院 数理学院，新疆 乌鲁木齐 830000)

Hamiltonian 系统广泛存在于数理科学，生命科学以及社会科学的各个领域，特别是经典力学与天体力学、等离子物理、航天科学以及生物工程中的很多模型都以Hamiltonian 系统(或它的扰动系统)的形式出现.近年来，含左右分数阶微分算子的方程在反常扩散的物理现象中有着广泛应用，例如分数阶对流扩散方程[1-2].其中，含有左右分数阶微分算子的Hamiltonian 系统成为分数阶微分方程理论中的一个新的领域，并取得了一系列解存在的结果[3-8].例如，Cesar Torres 在文献[8]中首次研究分数阶Hamiltonian 系统

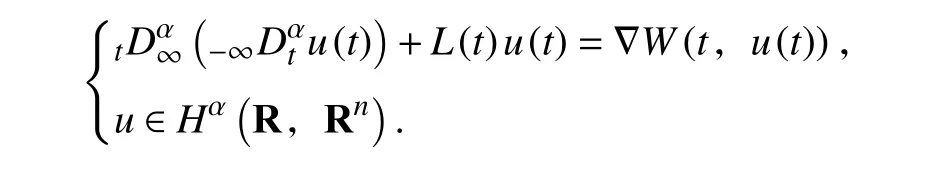
作者通过山路定理，在L(t)是正定且强制的条件下，得到上述系统至少有一个非平凡解.

Kirchhoff 方程是波动方程的扩展，该方程最早于1883 年由Kirchhoff[9]在研究弹性弦的自由振动时所提出.Kirchhoff 型微分方程在诸多领域都有广泛的应用，包括非牛顿力学、宇宙物理学、弹性理论电磁学及人口动力学等.近年来，国内外众多学者开始研究Kirchhoff 型方程问题，但由于Kirchhoff 项是非线性的且分数阶微分算子是非局部算子，这给(PS)条件的验证、Nehari 流形和值映射凸性的验证带来了一定的困难，从而导致Kirchhoff 型分数阶微分方程的研究比较复杂，与该方程有关的研究工作也不多[10-19].

受以上文献启发，本文研究如下一类Kirchhoff 型分数阶Hamiltonian 系统(简记为KH)

通过构造合适的分数阶空间，在对称矩阵L(t)满足半正定的条件下，给出新的嵌入定理及几个重要的不等式，利用临界点理论，研究上述系统基态解的存在性和集中性.

1 预备知识

2 系统(1)基态解的存在性

注4由于Kirchhoff 项是非线性的，这给PS 条件的验证带来了一定的困难.此外，当a=1，b=0时，KH(1)退化为文献[17]所研究的不带Kirchhoff 项的问题.

3 系统(1)基态解的集中性