一类二阶中立型时滞微分方程的振动性

赵玉萍

(青海民族大学 数学与统计学院，青海 西宁 810007)

考虑二阶非线性中立型时滞微分方程

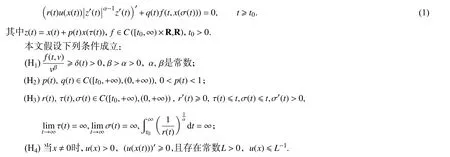
函数x(t)称为方程(1)的一个解，如果函数z(t)和r(t)u(x(t))|z′(t)|α-1z′(t)连 续可微且在区间 [t0，∞)上x(t)满足方程(1).方程(1)的一个非平凡解称为振动的，如果它有任意大的零点，否则，称它为非振动的.方程(1)的一切解均振动，则称方程(1)为振动的.

近年来，二阶非线性中立型时滞微分方程被广泛应用在智能机器人、天体物理、动力系统和其他高新技术领域中，许多学者对其振动性的研究产生了浓厚兴趣[1-11].Agarwal[1]研究了二阶半线性中立型时滞微分方程

的振动性.

吴英柱[2]将上述方程进行了扩展,研究了二阶非线性中立型时滞微分方程

的振动性，给出了多个振动定理,改进了文献[1]的结果.

武秀丽[3]研究了二阶非线性中立型时滞微分方程

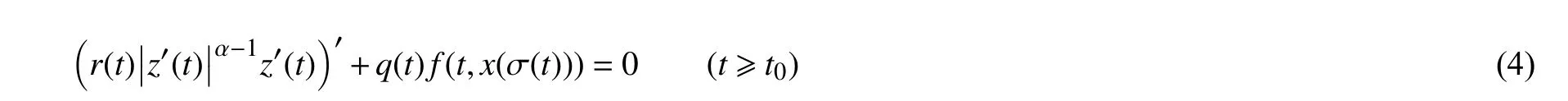
的振动性，获得了3 个振动定理，进一步改进了文献[2]的结果.方程(2)～(4)都是本文所考虑方程(1)的特例，本文借助Riccati 变换、微分中值定理和不等式技巧研究方程(1)的振动性，建立新的振动准则，推广和改进了现有文献的研究结果，本文研究的方程更广泛.

1 基本引理

为了证明文中的结果，先介绍下面几个引理.

2 主要结果

定理 1设条件(H1)～(H4)成立，若存在函数 φ (t)∈([t0,+∞),R+)，使得

其中B(t)=q(t)δ(t)(1-p(σ(t)))β，则方程(1)振动.

证明设x(t)是方程(1)的非振动解，不失一般性，设x(t) 为 [t0,∞)上 的正解(x(t)＜0的情况类似可证)，对引理3 中的(13)式从t0到t积分，得

当t→∞时，由已知得w(t)→-∞，这与w(t)＞0矛盾.定理3 证毕.

下面用Philos 型积分平均给出定理4，考虑集合D={(t,s):t≥s≥t0}，D0={(t,s):t＞s≥t0}.

函数H∈C(D,R)，称为属于D类，记做H(t,s)∈X，如果H满足下列条件：

其中B(t)=q(t)δ(t)(1-p(σ(t)))β，则方程(1)振动.

证明设x(t)是方程(1)的非振动解，不失一般性，设x(t) 为 [t0,∞)上 的正解(x(t)＜0的情况类似可证)，由引理2 中的(12)式和(H4)，可得

3 结果的应用