求解单调变分不等式的新次梯度外梯度算法

杨澈洲, 贺月红, 龙宪军

(重庆工商大学 数学与统计学院, 重庆 400067)

设H为实Hilbert空间,C⊆H是非空闭凸子集,〈·,·〉和‖·‖分别表示H中的内积和范数.设x∈H,PC(x)表示向量x在C上的投影,F:H→H是一个映射.本文考虑如下变分不等式问题：寻找点x*∈C,使得

〈F(x*),x-x*〉≥0, ∀x∈C.

(1)

(2)

该算法每次迭代需要计算2次到C上的投影和映射F在2个点的函数值.若C是一个一般的闭凸集或者F的值比较复杂,则会影响算法的计算效率.为了克服这一缺点,Censor等[6]提出了次梯度外梯度算法,该算法通过投影到一个半空间，简化了算法(2)中第二次投影的计算量,但在每次迭代时仍然需要计算映射F在2个点的函数值.因此,为了进一步减少计算成本,Malitsky等[7]提出了如下的修正次梯度外梯度算法

(3)

近年来,为了解除Lipschitz常数对算法步长的限制,学者们进行了大量的研究,见文献[8-9].Yang等[8]在如下算法中采用了一种新的自适应步长规则

(4)

其中

λn+1:=

该算法要求映射F是强单调且Lipschitz连续的,保持映射计算量的同时,不要求Lipschitz常数已知.随后,Hieu等[9]进一步将映射F的强单调弱化为单调,提出了如下算法

(5)

其中

λn+1:=

该算法要求映射F的Lipschitz连续性,但是在实际中许多函数并不是Lipschitz连续的.因此,如何在更弱的条件下给出新的投影算法并证明算法的收敛性是本文讨论的重点.

受文献[7-9]的启发,本文提出了一种新的次梯度外梯度算法求解变分不等式问题.该算法引入Armijo线性搜索准则,在映射F是单调和一致连续的假设下,证明了由算法产生的无穷序列弱收敛到变分不等式问题的解,并用数值实验验证了算法的适用性.本文所得结果改进和推广了文献[7-9]中相应的结果.

1 相关定理及引理

设C⊆H是非空闭凸子集,x∈H,定义

PC(x)=argmin{‖y-x‖|y∈C}

为x在集合C上的投影.

定义 1.1[10]设F:H→H是映射,如果对任意的x,y∈H,有

〈F(x)-F(y),x-y〉≥0,

则称F是单调的.

引理 1.1[11]设C⊆H是非空闭凸子集,则:

(i) 对任意的x∈H,y∈C,有

〈x-PC(x),y-PC(x)〉≤0;

(ii) 对任意的x∈H,y∈C,有

‖PC(x)-y‖2≤‖x-y‖2-‖PC(x)-x‖2.

引理 1.2[8]设{an}、{bn}是2个非负实序列,∃N>0,∀n>N,满足an+1≤an-bn,则{an}有界且

引理 1.3[12]设C⊆H是非空闭凸子集,F:C→H为单调连续算子，则x*∈VI(F,C)当且仅当

〈F(x),x-x*〉≥0, ∀x∈C.

引理 1.4[7]设H中的序列{xn}弱收敛于x∈H,则对任意的y∈H{x},有

2 算法及收敛性证明

为了引入本文的算法,需要下述条件:

条件 2.1C为非空闭凸集.

条件 2.2VI(F,C)非空,即VI(F,C)≠∅.

条件 2.3F:H→H是单调的,在C中的有界集上是一致连续的且在C上是弱序列连续的.

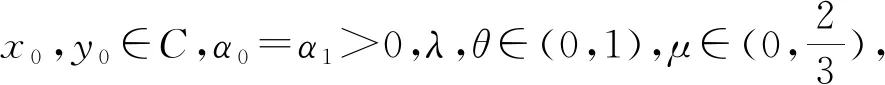
步骤1计算

并给定xn、yn-1、yn和αn,构造半空间

Hn={z∈H:〈xn-αnF(yn-1)-yn,

z-yn〉≤0},

转步骤2.

步骤2取αn为最大的

α∈{λθln|ln∈N0∪{0},n≥0},

其中ln是使得下式成立的最小非负整数

λθln〈F(yn-1)-F(yn),xn+1(α)-yn〉≤

(6)

其中

xn+1(α)=PHn(α)(xn-αF(yn)),

Hn(α)=

{z∈H:〈xn-αF(yn-1)-yn,z-yn〉≤0},

转步骤3.

步骤3计算

若xn+1=xn且

yn+1=yn=yn-1,

则停止;否则,令n:=n+1,返回步骤1.

注 2.1容易得到C⊆Hn.事实上,假设z∈CHn,则

〈xn-αnF(yn-1)-yn,z-yn〉>0,

这与

yn=PC(xn-αF(yn-1))

矛盾,故C⊆Hn.

注 2.2若算法满足停机准则xn+1=xn且

yn+1=yn=yn-1,

则

yn∈VI(F,C).

证明若算法中xn+1=xn,则根据算法中

xn+1=PHn(xn-αnF(yn)),

可知存在如下关系式

〈xn+1-(xn-αnF(yn)),z-xn+1〉≥0,

∀z∈C,xn+1∈C,

即

〈F(yn),x-xn〉≥0, ∀x∈Hn.

由于xn+1∈Hn,yn=yn-1,同时根据算法中半空间所述不等式得

〈xn-αnF(yn)-yn,xn-yn〉≤0.

因此,有

〈αnF(yn),xn-yn〉≥

〈xn-yn,xn-yn〉≥0.

由于

〈F(yn),x-xn〉=〈F(yn),x-yn〉-

〈F(yn),xn-yn〉≥0, ∀x∈Hn.

因此,有

〈F(yn),x-yn〉≥〈F(yn),xn-yn〉, ∀x∈Hn,

所以yn∈C⊆Hn,即yn∈VI(F,C).

引理 2.1假设条件2.1～2.3成立,则Armijo线性搜索准则(6)式有意义.

证明分如下2种情况讨论:

(i) 若yn∈C,考虑yn∈VI(F,C),则

由F的一致连续性知

则算法中步骤2所述不等式显然成立.

考虑yn∉VI(F,C),则存在n≥0使得

λθln〈F(yn-1)-F(yn),xn+1(α)-yn〉>

(7)

由柯西-施瓦茨不等式有

λθln‖F(yn-1)-F(yn)‖·

‖xn+1(α)-yn‖≥

λθln〈F(yn-1)-F(yn),xn+1(α)-yn〉,

(8)

结合(7)和(8)式有

λθln‖F(yn-1)-F(yn)‖>

(9)

对(9)式取极限可得

则获得了矛盾.

(ii) 若yn∉C,则假设线性搜索不能有限步终止,即存在n≥0使得(7)式成立,令n→∞,通过与上述类似推理可以得到矛盾.因此,Armijo线性搜索准则(6)式有意义.

引理 2.2设{xn}和{yn}是由算法2.1生成的2个序列,z∈VI(F,C),则

‖xn+1-z‖2≤‖xn-z‖2-

(10)

证明因为z∈VI(F,C)⊆Hn和

xn+1=PHn(xn-αnF(yn)),

由引理1.1知

‖xn+1-z‖2≤‖xn-αnF(yn)-z‖2-

‖xn-αnF(yn)-xn+1‖2=

‖xn-z‖2-‖xn-xn+1‖2-

2αn〈F(yn),xn+1-z〉.

(11)

根据F的单调性和z∈VI(F,C)可得

2αn〈F(yn),yn-z〉≥0.

(12)

将(12)式加到(11)式右边可得

‖xn+1-z‖2≤‖xn-z‖2-‖xn-xn+1‖2-

2αn〈F(yn),xn+1-yn〉=

‖xn-z‖2-‖xn-yn‖2-‖xn+1-yn‖2-

2〈xn-yn,yn-xn+1〉-2αn〈F(yn),xn+1-yn〉=

‖xn-z‖2-‖xn-yn‖2-‖xn+1-yn‖2+

2αn〈F(yn-1)-F(yn),xn+1-yn〉+

2〈xn-αnF(yn-1)-yn,xn+1-yn〉.

(13)

又因为xn+1∈Hn,则

〈xn-αnF(yn-1)-yn,xn+1-yn〉≤0.

(14)

另一方面,由(6)式和2ab≤a2+b2知

2αn〈F(yn-1)-F(yn),xn+1-yn〉≤

μ‖yn-1-yn‖·‖xn+1-yn‖≤

μ(‖yn-1-xn‖+‖xn-yn‖)‖xn+1-yn‖≤

2‖xn-yn‖·‖xn+1-yn‖)≤

2‖xn+1-yn‖2).

(15)

结合(13)～(15)式可得

‖xn+1-z‖2≤‖xn-z‖2-

(1-μ)‖xn+1-y

证毕.

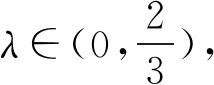
证明首先证明序列{xn}的收敛性.由(10)式知∃N≥0,∀n≥N使得

‖x

‖x

(16)

令

则(16)式可表示为

an+1≤an-bn, ∀n≥N.

再由引理1.2知,序列{an}有界且极限存在,由(16)式知,有界序列{an}是非增的,因为

故{an}为收敛序列.另一方面,由序列{bn}的定义知

(17)

则有

因为

故序列

{‖xn+1-yn‖2}

收敛.因为{an}与{‖xn+1-yn‖2}收敛,故序列

{‖xn-z‖2}

收敛.由此知序列{xn}有界且存在弱收敛于z∈H的子列{xnk}.由(17)式有{ynk}弱收敛于z∈C.

下证z∈VI(F,C).由引理2.1及序列{yn}的定义可得

〈ynk+1-xnk+1+αnF(ynk),x-ynk+1〉≥

0, ∀x∈C.

上式等价于

0≤〈ynk+1-xnk+1,x-ynk+1〉+

αn〈F(ynk),ynk-ynk+1〉+αn〈F(ynk),x-ynk〉.

令n→∞,由(17)式及{ynk}弱收敛于z∈C可知,αn〈F(ynk),x-ynk〉≥0,即

〈F(z),x-z〉≥0, ∀x∈C,

故z∈VI(F,C).

‖x

‖x

因此,对所有x∈VI(F,C)有

再由引理1.4可知

注 2.3本文从以下2个方面改进了文献[7]中的结果:

1)F的Lipschitz连续性弱化为一致连续;

2) 本文采用Armijo线性搜索准则避免要求Lipschitz常数已知这一假设.

注 2.4本文从以下2个方面改进了文献[8]中的结果:

1)F的强单调性弱化为单调性;

2)F的Lipschitz连续性弱化为一致连续.

注 2.5本文采用Armijo线性搜索准则弱化了文献[9]要求Lipschitz连续这一条件.

3 数值实验

本文数值实验的测试环境为Matlab 2019a,Windows 10系统Intel(R)Core(TM)i7-6700HQ CPU@2.60 GHz和8.0 GB.为了体现本文算法的数值效果,采用2个例子进行算法对比.这里“K”代表最大迭代次数,“iter”代表迭代次数,“time”代表程序的CPU运行时间,单位为s.选取参数如下:

λ=0.5,θ=0.4,μ=0.45.

例 1考虑映射F:R2→R2满足

F(x)=(x1+x2+sin(x1),-x1+x2+sin(x2)),

∀(x1,x2)∈R2.

令

C={x=(x1,x2)∈R2|-2

初始点x1、x2随机产生,选取

‖xn‖≤err=10-4

为停机条件.在此条件下,对几种算法进行比较,具体数值实验结果如表1所示.

表1 不同算法关于例1的比较

例 2现考虑

C:={x∈H:‖x‖≤2}.

令g:C→R有如下定义

g是Lipchitz连续且

考虑映射F:L2([0,1])→L2([0,1])是有界且单调的,同时满足

∀u∈L2([0,1]),t∈[0,1].

定义A:C→L2([0,1])满足

A(u)(t):=g(u)F(u)(t), ∀u∈C,t∈[0,1].

‖xn+1-xn‖≤err=10-4.

在此条件下,对几种算法进行比较,具体数值实验结果如表2所示.

表2 不同算法关于例2的比较

(i) 本文算法、文献[8]算法、文献[9]算法均收敛到变分不等式问题的解,见表1和表2;

(ii) 从迭代次数以及程序CPU运行时间来看,本文算法优于文献[9]算法和文献[8]算法,尤其是本文算法充分体现了CPU运行时间较少的优势,见表1和表2;

(iii) 在适当参数的选取下,对比例1和例2发现最大迭代次数K对本文算法的影响较小,见表2.

致谢重庆工商大学科研项目(ZDPTTD201908)对本文给予了资助，谨致谢意.