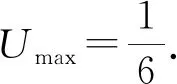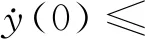一个偶极量子气体爆破的新准则

王洪莉, 黄 娟*

(1. 四川师范大学 数学科学学院, 四川 成都 610066; 2. 四川师范大学 可视化计算与虚拟现实四川省重点实验室, 四川 成都 610066)

考虑如下描述偶极量子气体的Gross-Pitaevskii方程

(1)

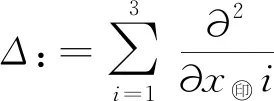
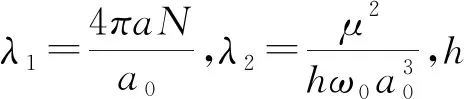
其中θ=θ(x)是x∈R3和偶极轴n∈R3(|n|=1)间的夹角,即cos如果n=(0,0,1),则对x=(x1,x2,x3)∈R3,其偶极相互作用核还可以表达为

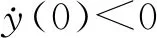
(2)

本文先介绍一些预备知识,如方程的局部适定性和varial恒等式等;然后给出本文的主要结论及证明.

1 预备知识

对于方程(1),定义如下空间

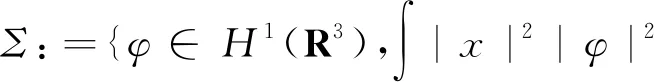
其中H1(R3)=W1,2(R3)是Sobolev空间，其内积和范数分别是

〈φ,φ〉

下面,将回顾Cauchy问题(1)的局部适定性.

命题 1.1对λ1,λ2∈R,φ0∈Σ(R3),存在时间T+,使得Cauchy问题(1)有唯一解

φ∈{φ∈C([0,T+];H1(R3));φ,▽φ,xφ∈

即要么T+=+∞(整体存在),要么T+<+∞,(爆破).当t∈[0,T+)时,Cauchy问题(1)的质量泛函和能量泛函是守恒的:

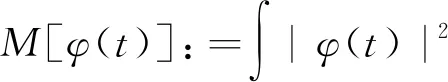
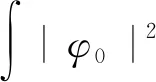
(3)

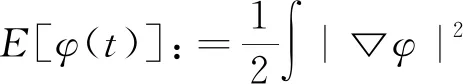
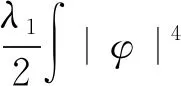
(4)

其中

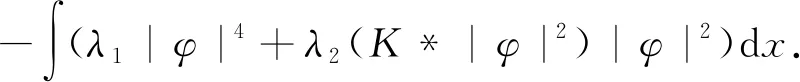
引理 1.1令φ0∈Σ(R3),φ是方程(1)的解.设

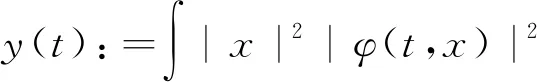
当y(0)<∞时,下列等式成立:

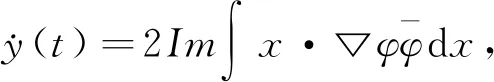
(5)

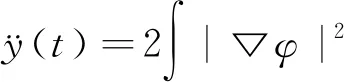
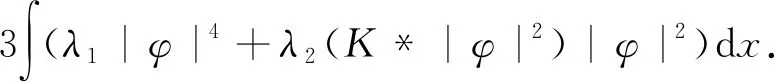
引理 1.2[5]假设λ1、λ2满足(2),对任意φ∈H1(R3),都有Φ(|φ|2)≥0(当φ(x)=0时,Φ(|φ|2)=0)，即

其中σ>0满足

2 爆破条件

定理 2.1假设φ0∈Σ(R3),y(0)<∞,E[φ0]>0.若满足

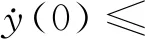
其中ω2=min且

(7)

则Cauchy问题(1)的解将在有限时间内爆破.

证明由(4)和(6)式知

λ2(K*|φ|2)|φ|2)dx=

通过引理1.2得

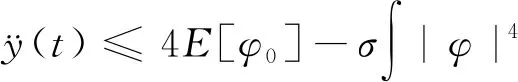
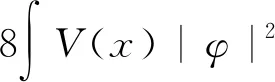
(9)

又有ω2=min结合内插不等式可得

‖φ‖

(10)

则(9)式可化为

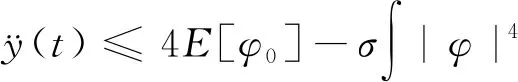
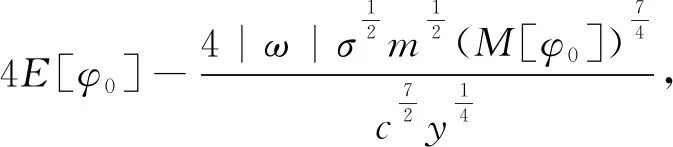
t∈[0,T+).

(11)

令y(t)=ymaxν(s),s=at,其中

y

(12)

再由(11)式可知

ν

(13)

利用Lushnikov在文献[16]中提出的一个粒子在带势垒的场中运动的力学类比,(13)式可重新记为:

νss=F1+F2,s∈[0,T+/a),

(14)

这里ν=ν(s)是在带势垒场中运动的粒子,它受F1和F2两个力的作用,其中，

为粒子ν的电势,F2=-g2(s)是一个将粒子ν拖向零点的未知力.若粒子在有限的时间内到达零点(ν(s*)=0,0

ν

(15)

定义粒子ν的能量

(16)

1)ε(0)

2)ε(0)>Umax,νs(0)<0;

3)ε(0)=Umax,νs(0)<0,ν(0)<1.

由ε

1)⟺-f(ν(0))<νs(0)

2)⟺νs(0)<-f(ν(0));

3)⟺ν(0)<1,νs(0)=-f(ν(0)).合并条件1)～3),得

ν

(17)

由y(t)=ymaxν(at),可推出

综上可得

其中g由(7)式定义.