磁驱动双半球胶囊机器人爬坡运动分析*

陈自强，张永顺

（大连理工大学精密与特种加工教育部重点实验室，辽宁大连 116024）

0 引言

胶囊内窥镜相较传统胃镜具有诊断无痛、安全的优点，被广泛应用在胃肠道疾病检查中。虽然目前以Given ImagingLtd的M2A和金山科技初代的OMOM为代表的国内外胶囊机器人已技术成熟且投入商用，但它们大多数依靠胃肠道蠕动行进，位姿随意性强，漏检率高[1]。因此开发可灵活行走且姿态可控的主动式胶囊内窥镜便尤为重要。

目前主动式胶囊机器人驱动方式主要分为执行机构驱动和永磁体驱动，前者结构复杂，不利于胶囊微型化的同时也存在电源模块工作时长受限的问题，后者则由于受制梯度磁场而较难实现胶囊位置与姿态的分离控制。本课题组利用已有的三轴亥姆霍兹线圈装置产生的空间均匀万向旋转磁场与胶囊内嵌永磁体耦合生成的磁力矩驱动整体实现自旋与前进后退[2-4]。随动效应[5]使机器人轴线可以时刻跟随磁矢量法线方向，借此实现胶囊被动模态的悬停调姿和主动模态的滚动行走，控制更加灵活。

常规球形机器人依靠摆锤或配重块等改变重心来驱使整球滚动，其平面滚动速度和爬坡能力受制于偏心装置的质量占比，爬坡效果不理想[6]。将耦合磁力矩作为驱动源，本文中的机器人具备更好的爬坡效果。

为使采集的图像稳定可用，胶囊机器人爬坡时需有良好的抗干扰能力。描述机器人位姿的状态变量互不独立，是典型的非完整性约束系统，动力学建模工作更加复杂。

本文采用拉格朗日乘子法建立描述机器人爬坡的完整动力学模型，分析与姿态角相关的夹角变化，说明了机器人的抗干扰能力。建立简化爬坡动力学模型分析爬坡角度。理论分析和试验结果为改善和提高机器人爬坡性能提供了理论支持。

1 机器人结构

如图1所示，内置轴承实现主动半球壳体和被动半球壳体的悬浮连接，保证两半球间的相对转动。NeFeB永磁体与主动半球壳固连，当外部磁场旋转时，受到磁力矩驱动的永磁体带动主动半球一同旋转，与摄像头定位器件等固连的被动半球因无动力而不旋转。为实现图像采集等功能，零件还包括发射天线、LED电路、摄像头、电池、电路板等。当机器人轴线因随动效应而随磁场轴线变为水平方向时，与肠道接触的主动半球将借助摩擦力带动整球一同滚动[7]。

图1 双半球胶囊机器人结构

2 爬坡完整动力学建模与动态特性分析

2.1 建立坐标系

机器人涉及姿态变化的爬坡过程如图2所示。

图2 爬坡运动示意图

各坐标系情况如图3所示。

（1）如图3（a）所示，OXYZ为惯性坐标系，OX轴与水平面重合。旋转磁矢量B绕原点O在XOZ面内旋转，磁矢量法线nB方向与OY轴平行。

（2）OX1Y1Z1为固定坐标系，OX1轴与水平面夹角为θ。（x,y）为机器人球心o在OX1Y1Z1内的坐标。

（3）ox0y0z0为平动坐标系，坐标系原点o与球心重合。

（4）oxyz为描述机器人位姿的赖柴坐标系。如图3（b），先绕oz0轴旋转α角得到中间坐标系oxy1z0，再绕ox轴旋转β角得到赖柴坐标系。机器人的轴线n最终与oy轴重合。

图3 各坐标系示意图

（5）ox1yz1为机器人本体坐标系。由坐标系oxyz绕y轴旋转γ角得到。

为描述机器人爬坡时包含姿态变化的完整动力学方程，有广义坐标：坐标x、y，姿态角α、β及γ。设机器人半径为R，质量为m，机器人和坡面的接触点为P，内嵌永磁体磁矩为m0，旋转磁矢量强度幅值为B0。

2.2 非完整性约束方程

假设机器人爬坡全过程为纯滚动[8]。角速度经一系列坐标变换后，在坐标系ox0y0z0中可表示为：

在坐标系ox0y0z0中，矢量oP表示为：

纯滚动时，速度瞬心点P的速度表达式为：

于是点o速度为：

将式（1）代入式（4），得非完整约束方程：

2.3 磁力矩与阻力矩计算

如图3（a）所示，磁矢量B的旋转速度为ω，在惯性坐标系OXYZ中的表达式为：则经过坐标转换，B在赖柴系oxyz中为：

其中：

A=sin α cos β cos θ+sin θ sin β

B=sin β cos θ-sin α cos β sin θ

C=sin α sin β cos θ-sin θ cos β

D=sin α sin β sin θ+cos β cos θ

和机器人固连的永磁体磁矩m在oxyz中表示为：

式中：ε为转差角，即机器人旋转时磁矩矢量滞后磁矢量的角度。

参考磁力矩公式T1=m1×B1，得到T1在赖柴系oxyz中的分量表达式：

其 中：E=B0cos α cos θ sin ωt+B0cos α cos ωt sin θ,F=B0 cos ωt(cos β cos θ+sin α sin β sin θ)。

爬坡时，阻力矩包括机器人壳体与肠道相对滑动受到的粘性摩擦力矩，以及静摩擦力所产生的摩擦阻力矩。设粘性阻尼系数为k，静摩擦力为mgsinθ，则阻力矩Mf在赖柴系oxyz中可表示为：

式中：k0、i、j分别为z0、x、y轴的单位向量。

2.4 爬坡完整动力学方程

非完整约束使得广义坐标之间失去独立性，拉格朗日乘子法可以很好解决此问题，其表达式为：

式中：L为拉格朗日函数；qα为广义坐标；Qα为广义力；λr为拉格朗日乘子；fr为非完整约束方程。

经变换，oxyz中机器人角速度ω1表示为：

设T为系统动能，其包括平动动能和转动动能，联立式（5）（12）有：

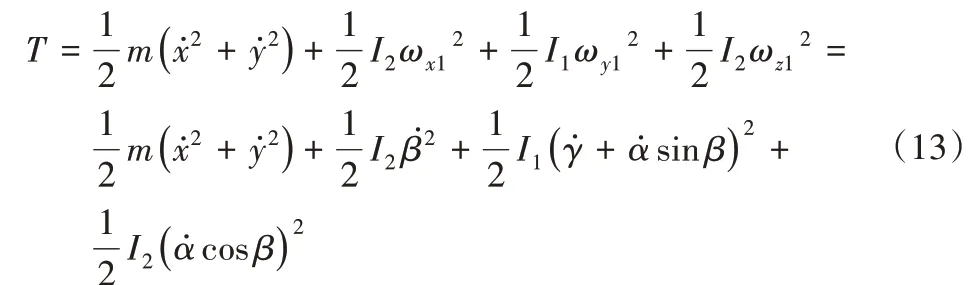
式中：I1为极转动惯量；I2为赤道转动惯量。

取水平面为零势能面，则势能V为：

式中：s为球心位移在OX1方向的投影，即x。

拉格朗日函数L=T-V，其表达式为：

则机器人主动模态下的爬坡完整动力学方程为：

为了方便分析机器人的姿态角响应特性，取状态变量x=（α，β，）T。当机器人爬坡滚动不丢步时，可将自转角γ替换为ωt-ε，于是可得到˙=f(x,t)·x形式的方程组：

其中：

式（17）即为可以描述姿态角变化的微分方程组。

2.5 爬坡动态特性分析

将旋转磁矢量所属平面的法线nB（磁场轴线）调整为水平时，借助随动效应，机器人的轴线n可以近乎时刻与nB重合，进而以主动模态完成爬坡运动。然而胃肠道空间并不宽裕，机器人在行进时难免受到胃肠壁刮蹭等环境干扰。将n与nB间的夹角σ作为反映机器人轴线偏离目标方位的目标函数，其与姿态角α、β之间的数学关系为：

给定初值不同的σ来模拟实际作业时受到的环境干扰，结合式（17）线性化后的微分方程组分析机器人轴线姿态回归的能力。具体仿真参数如表1。

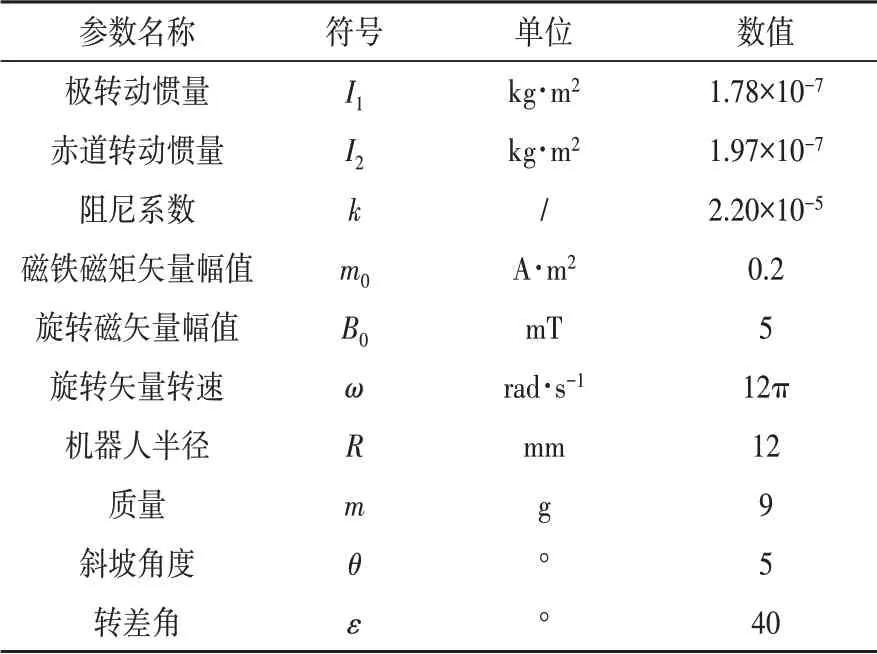
表1 仿真参数取值

从图4中可以看到，在90°极限范围内，无论初值σ选取多大，经一段时间后都能收敛于0°，且σ的初值越小，其回归的也越快。这表明受到干扰时，机器人具备回归稳态的能力，这为机器人的多场景稳定行走提供了理论支持。

图4 不同初值时σ的时间响应曲线

3 爬坡运动平面动力学建模与爬坡能力分析

3.1 前向爬坡动力学建模

为了方便探究机器人的爬坡能力，可以建立不含姿态角的坡面运动动力学方程。如图5所示，建立坐标系OX2Y2。

图5 球形机器人爬坡运动简化模型

取爬坡位移s为广义坐标，滚动摩阻为M0，机器人绕转轴的转动惯量为I1，滚过角度为φ。故有关系：

考虑到轴承间粘性阻尼不可忽略，采用基于能量耗散的拉格朗日方程，形式如下：

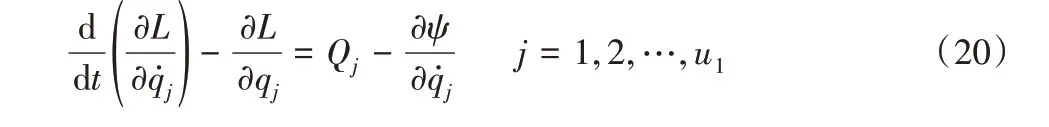
系统动能Ta为：

取水平面为零势能面，则任意位置的势能Va为：

耗散函数ψ：

式中：k1为轴承间的粘性摩擦因数。

机器人受到的主动力包括：耦合磁力矩T2、重力mg以及滚动摩阻M0。根据虚功原理，广义力可表示为：

式中：σ0为滚动摩阻系数；引入符号函数sgn，旨在滚动摩阻方向时刻与角速度方向相反。

最终可得到平面动力学方程：

3.2 纯滚动条件分析

机器人在攀爬大角度时往往容易打破纯滚动状态而发生滑动甚至原地空转，这影响了机器人跟随磁场的能力，造成和理论设定速度的偏差，产生速度损失，因此分析纯滚动时的最大爬坡角度更具意义。机器人纯滚动时，受力如图6所示。

图6 胶囊机器人斜面纯滚动时的受力模型

假设机器人向右滚动，角加速度为α，质心C的加速度为aC，静摩擦力为f，静摩擦因数为fs。根据动量矩定理可得[9]：

式中：滚动摩阻M0=σ0mgcosθ；因为aCy=0，故aCx=aC；点P为速度瞬心，故有aC=αR。

纯滚动时满足：f≤fsFN，也即f≤fsmgcosθ。结合上述条件，可得纯滚动条件为：

对式（27）进行整理，可得：

3.3 爬坡能力仿真

固定参数ω=12π rad/s，I1=1.78×10-7kg·m2，取磁场强度B0的仿真上限为12 mT[10-11]，利用Matlab对式（25）进行仿真，得到图7所示关系曲线。

图7 爬坡角度和磁场强度关系曲线

可以看到，随着磁场强度B0的增大，机器人的最大爬坡角度也变大，爬坡能力增强。

保持磁场强度B0=8 mT，结合式（28），仿真得到各个爬坡角度下纯滚动时所需的最小静摩擦因数曲线。由图8可知，爬坡角度越大，纯滚动时所需的静摩擦因数越大。当肠道环境达不到对应爬坡角度所需的最小静摩擦因数时，机器人便发生打滑甚至空转。

图8 最小静摩擦因数与角度关系曲线

为更好地说明纯滚动转变为滑动的条件，保持B0分别为8 mT、9 mT、11 mT，仿真得到图9。人体肠道的静摩擦因数fs为0.6左右[12]，故以0.6作为对照值。当B0=8 mT时，由图7可知，此时机器人的爬坡角度为17°，在图9中找到17°时保证纯滚动的最小静摩擦因数fsmin=0.47，小于0.6，因此机器人可以按设定速度爬坡。同理，B0=9 mT对应的坡角为21.5°，参照图9，此时满足纯滚动所需的fsmin=0.54，同样小于肠道可以提供的最大静摩擦因数。当B0=11 mT时，爬坡角度为30°，此时纯滚动所需的fsmin=0.725，大于肠道所能提供的最大静摩擦因数，因此机器人将发生打滑甚至空转。

图9 不同B0对应的爬坡角度与摩擦因数的关系曲线

结合纯滚动要素，绘制不同静摩擦因数下机器人纯滚动的最大爬坡角度与磁场强度关系曲线。从图10可知，在几种典型肠道静摩擦因数中，静摩擦因数越大，机器人的爬坡极限值越大，爬坡表现越好。

图10 典型静摩擦因数下最大爬坡角度曲线

4 结束语

本文的创新点在于根据拉格朗日乘子法建立了磁驱动胶囊机器人主动模态爬坡时的完整动力学方程，通过仿真机器人轴线回归预设方位情况说明了机器人的抗干扰能力；根据基于能量耗散的拉格朗日动力学原理建立二维爬坡动力学模型，结合纯滚动条件仿真磁场强度与肠道静摩擦系数对于爬坡能力的影响规律。

仿真结果表明：机器人爬坡时具备良好的姿态回归能力，其抗干扰特性为保证机器人爬坡的顺利行走及稳定图像采集功能奠定了基础；在一定范围内，磁场强度越大，机器人的爬坡表现越好，大的肠道静摩擦因数将增大机器人的最大不打滑爬坡角度，这一结论对于改善机器人在大坡度时的打滑问题提供了解决思路，对于未来越障方面的研究也具有参考价值。