一类线性二次时间不一致控制问题*

计 伟

(贵州建设职业技术学院信息管理学院，贵州 贵阳 551400)

0 引言

我们从线性二次最优控制问题的叙述开始。设T>0和U⊆Rm，定义

D[0，T]={(s，t)∈[0，T]×[0，T]│0≤s≤t≤T}

和

u[t，s]=L2([t，s]；Rm)≡{u：[t，s]→

对固定y0∈Rn，考虑以下线性控制系统：

(0.1)

其中，C(·)∈L∞([0，T]；Rn×n)，D(·)∈L∞([0，T]；Rn×m)，显然，对∀u(·)∈u[0，T]，控制系统存在唯一解：

性能指标为：

〈M(s，s)u(s)，u(s)〉]ds

(0.2)

其中，L∈L∞(D[0，T]；Sn)，M∈L∞(D[0，T]；Sm)。这里Sn表示n×n阶实值对称矩阵全体。最优控制问题为：

问题(LQ)。对于系统(0.1)，在控制集u[0，T]中求控制函数，使得性能指标(0.2)最小化。即：

问题(LQ)最显著的特征是时间一致性，也就是对固定的初始对(0，y0)，求得最优解后，沿着最优轨道，在任意时刻对应的控制都是最优控制。但是，由于社会环境的复杂变化和决策者决策心态的改变，现实问题并不是如此简单和完美，往往表现为时间不一致性。事实上，时间不一致问题远多于时间一致问题，并且时间一致问题可以看着是时间不一致问题的一个特例[1]。时间不一致控制问题的例子可见文献[2，3]。

关于时间不一致控制问题里程碑似的研究工作是Strotz[4]于1955年对时间不一致控制问题的数学公式化。在这之后，由于时间不一致控制问题具有重要的理论价值和应用价值，大量数学家和金融学家对其展开研究，尤其是近年来，取得了丰硕的研究成果[5-15]。但是，正如著名行为金融学家周迅宇教授指出：关于时间不一致问题的研究远未成熟，现尚处于初期探索阶段。

1 数学模型和预备知识

对∀(t，y)∈[0，T]×Rn，考虑以下线性控制系统：

(1.1)

以及如下性能指标：

(1.2)

考虑如下的控制问题：

问题(TILQ)。对于系统(1.1)，在控制集u[0，T]中求控制函数，使得性能指标(1.2)最小化，即：

因为问题(TILQ)对初始时间t的依赖性，这意味着随着控制的进行，问题(TILQ)的性能指标甚至控制系统会因为时间t的变化而变化。因此，对问题(TILQ)的优化问题并不是简单地优化一个问题，而是优化一族问题，显然，问题(TILQ)不同于经典问题(LQ)。

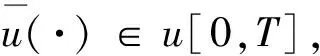
对∀t∈[0，T]，ε>0和v∈U。其中，

我们引入如下假设条件：

(L1)：设L：D[0，T]→Sn和M：D[0，T]→Sm连续，并且对某个常数δ>0有：

L(t，s)≥0，M(t，s)≥δI，(t，s)∈D[0，T]

存在一个常数l>0，使得：

|L(t1，s)-L(t2，s)|+|M(t1，s)-M(t2，s)|≤l|t1-t2|，∀t1，t2，s∈[0，T]

2 主要结果

命题2.1 设(L1)成立，对任意给定的初始对(t，y)∈[0，T]×Rn，则方程组：

(2.1)

存在解φ∈C([0，T]；Rn)。

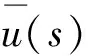
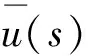
(2.2)

(2.3)

因为t固定，方程组(2.3)显然可解(文献[16])，这意味着方程组(2.1)至少存在一个解，不妨记为：

其中，

定理2.2 设(L1)成立，设y0∈Rn固定，则问题(LQ)的最优控制是问题(TILQ)的均衡控制。

(2.4)

由(2.1)式，我们有：

又因为M是正定矩阵，所以：