高心墙堆石坝接触黏土与混凝土基座接触特性研究

朱雨萌，李国英，陈子玉，秦育阳，陈 忍

(1. 南京水利科学研究院，南京 210029；2. 河海大学，南京 210098)

0 前 言

心墙堆石坝因其施工成本低、坝基适应性好以及可以利用当地材料等优点，成为世界各国广泛采用的坝型。然而心墙与混凝土垫层之间力学特性差别较大，容易产生不均匀沉降和应力集中，使心墙与混凝土垫层之间出现较大的剪切变形[1-2]。因此，需在心墙与混凝土垫层接触处设置柔性较好和适应变形能力较强的接触黏土。

直剪试验是探究土-结构物接触面力学特性的重要研究手段[3-5]，其物理机制清晰，测试方法简单。已有研究成果表明，结构物表面粗糙度、结构物种类、平均粒径、相对密度、法向应力、温度效应以及剪切速率均对土-结构接触面力学特性有着重要影响[6-9]。Tatsuoka和Haibara[10]通过一系列直剪试验研究了不同的砂土与光滑结构物接触面抗剪强度。Taha和Fall[11]研究结果表明，超固结比、干密度和含盐量对敏感海相黏土的接触面剪切行为有显著影响。Hamid和Miller[12]认为非饱和土与钢板接触面的抗剪强度与基质吸力有关。Al-Douri和Poulos[13]研究了单调与循环荷载作用下不同砂土与金属接触面的剪切特性。Pra-Ai和Boulon[14]探究了砂土与钢板接触面在常载荷和常刚度下的力学特性。以上试验结果表明，接触面在不同影响因素作用下表现出复杂的力学特性。

目前，针对心墙堆石坝中接触黏土与混凝土垫层接触面接触特性的研究较少。接触黏土与混凝土垫层接触面的剪切特性与粗糙度、应力状态、土体密实度以及含水率等有关。本文以采自LHK坝现场的接触黏土作为试验对象，结合室内试验和数值分析手段，对不同含水率与应力状态下的高心墙堆石坝接触黏土与混凝土垫层的接触效应进行研究，为高心墙堆石坝设计建设提供参考与技术支持。

1 接触面直剪试验

1.1 试验设备

试验采用自主研发的三维剪切试验设备。该试验设备主要由剪切盒、推力驱动设备、法向应力加载装置和控制测量系统等组成，法向应力最大可达1.2 MPa，最大剪切推力为2.4 kN，最大行程为10 cm，剪切速率为0.5 mm/min。试验全过程实现自动化控制与测量，测量精度为2% FS(满量程)。图1为三维剪切试验设备。

1.2 试验材料

接触黏土烘干后呈红褐色，颗粒为亚棱角状，通过X射线衍射分析，土壤样品的主要成分为SiO2，并掺有少量的CaAl2Si2O8·4H2O。其基础物理属性如表1所示。

表1 接触黏土基础物理属性

图1 三维剪切试验设备

1.3 试样制备与试验过程

试验采用重塑试样，具体制备方法如下：

(1) 将风干土样碾碎并过2 mm筛；

(2) 测定土样的风干含水率，同时计算目标含水率试样所需的加水量；

(3) 用喷雾器在风干土样表面上喷洒计算所需的加水量，将土样搅拌均匀后放入塑料袋内并将袋口扎紧，然后放置于玻璃缸内密封，湿润一昼夜以保证土样中水分均匀；

(4) 根据剪切盒体积以98%压实度来计算试样所需质量；

(5) 将湿土倒入环刀内，拂平土样表面，以静压力将土缓缓压入环刀内。

为了测量接触面试验中仅由剪应力引起的法向变形，在上剪盒上施加法向荷载，直至试样的法向变形稳定。在试样上施加法向压力之后，测量并记录试样的法向变形量，当法向变形量不大于0.005 mm/h时，认为已经达到固结稳定。试验以单向剪切作为试验手段，在试验过程中，各组试样的剪切速率均为 0.8 mm/min。

1.4 试验方案

为探究含水率和法向应力对接触黏土-混凝土接触面力学特性的影响，制备4组不同含水率w(12.5%、14.5%、16.5%、18.5%)的试样，对相同含水率的每组试样施加不同法向应力σn(200、 400、 600、 800 kPa)。所有试样压实度均为98 %，并进行了单向直剪接触面试验。同时，本研究亦对接触黏土进行了一系列直剪试验，以测定其抗剪强度。直剪试验工况与接触面试验工况相同，具体试验工况如表2所示。

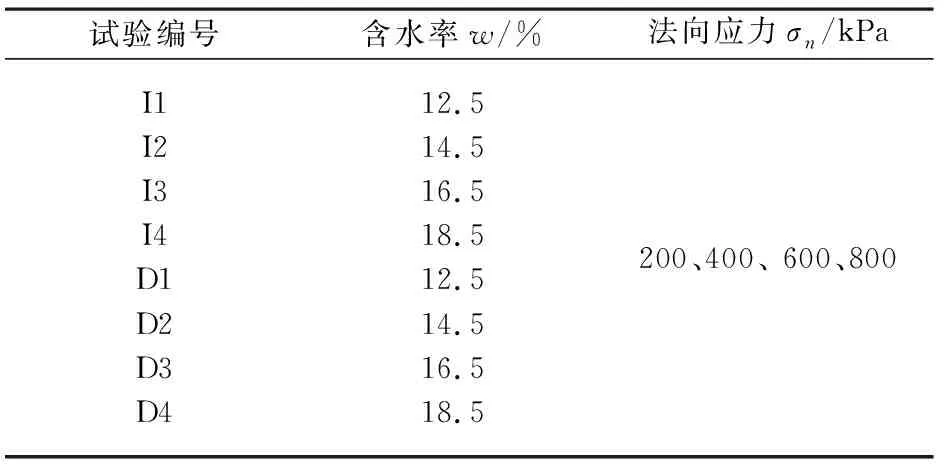
表2 试验工况

2 试验结果与分析

图2为接触黏土-混凝土接触面试验结果。如图2所示，接触面剪切应力应变关系大致呈双曲线趋势，并且大多数试样表现为应变硬化。在相同含水量条件下，抗剪强度对应的剪切应变随法向应力的增加而增大。

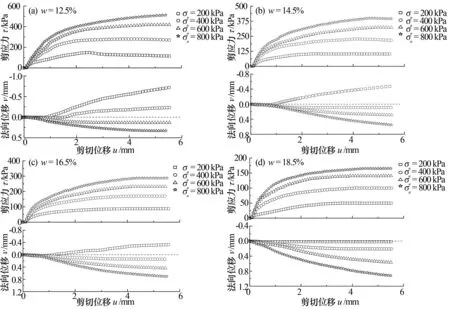
图2 接触黏土-混凝土接触面试验结果

剪切过程中法向变形以压缩为正，试验结果表明，接触面在低法向应力、低含水率时表现为剪胀现象。当含水率为12.5 %时，接触面法向变形在200 kPa和400 kPa下的表现为剪胀，当法向应力增大到600 kPa之后，法向变形表现剪缩特性。当含水率较高(w≥14.5 %)时，接触面在法向应力400 kPa下便表现为剪缩特性。因此，随着法向应力和含水率的增加，接触面的法向变形表现为明显的剪缩趋势。

接触黏土-混凝土接触面和接触黏土抗剪强度如图3所示。由图可知，在200 kPa和400 kPa法向应力下，接触面的抗剪强度明显小于黏土的抗剪强度。随着法向应力的增大，接触面的抗剪强度和黏土抗剪强度基本一致。试验结果表明，当法向应力较低时，接触面会沿着混凝土表面发生滑移破坏，而当法向应力较高时，接触面滑动面可能产生在黏土内部即接触面的破坏形式表现为黏土的剪切破坏。刘方成等[15]也得出了类似的试验结果，并认为接触面破坏模式决定了其应力应变关系发展模式。总体而言，法向应力越低、含水率越高，接触面的抗剪强度越低。

接触面剪切强度可表示为双线型Mohr-Coulomb强度准则:

(1)

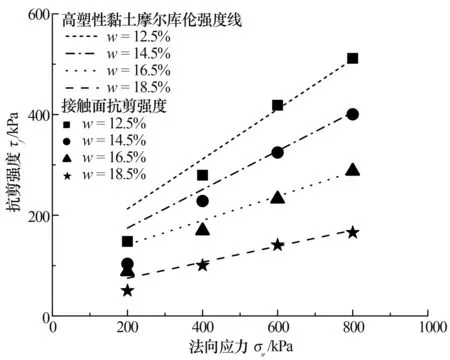
图3 接触面和接触黏土抗剪强度

3 接触黏土与混凝土接触面数学模型

3.1 数学模型

Desai等人[16]最早提出了薄层单元(有厚度)来模拟土与结构接触面：

(2)

公式(2)中:En和Gs分别为接触面的法向模量和剪切模量，kPa，其大小与法向应力、接触面材料、土体类型以及土体初始相对密度有关；Gsn和Ens分别表示法向变形过程引起的剪切变形模量和由剪切过程引起的法向变形模量，kPa。在直剪与单剪试验中，一般不考虑由法向应力引起的剪切应变，因此Gsn可以取0[17]。若不考虑应力路径的影响，En、Gs、Ens可通过压缩试验和直剪试验直接测得[18]。

剪切模量Gs反映接触面剪切特性，接触面剪切应力应变关系可用双曲线模型来表示:

(3)

公式(3)中:a1和b1是双曲线模型参数。与Clough和Duncan模型相似，a1和b1分别为:

(4)

(5)

公式(4)～(5)中:Gsi是初始剪切模量,kPa;τu是γ→∞时的剪应力，K1、n1和Rf为接触面材料参数。对公式(3)进行微分并结合公式(4)和公式(5)，剪切模量Gs的表达式为：

(6)

公式(6)表示:Gs随法向应力增加而增加。式中包含7个参数，φi、Ci、φc、Cc为接触面和黏土强度指标，K1、n1和Rf可由试验数据拟合得到。所有参数均可根据不同法向应力下直剪试验结果确定。

基于接触面试验结果，接触面的法向应变和剪切应变关系采用分段函数进行拟合，即剪胀关系用二次函数拟合，剪缩关系用双曲线函数拟合，其表达式为：

(7)

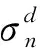
法向切线模量Ens可以表示为：

(8)

公式(8)中:H1、H2、M1和M2的表达式为：

(9)

(10)

(11)

(12)

3.2 模型验证

根据接触黏土与混凝土接触面的直剪试验结果，采用所建议的模型分别对剪应力和法向位移进行拟合，以验证模型的合理性。模型参数的拟合结果如表3所示，试验结果与模型计算结果的对比如图4所示。由图4可知，该非线性弹性模型能够较好地模拟接触黏土与混凝土接触面的力学特性。

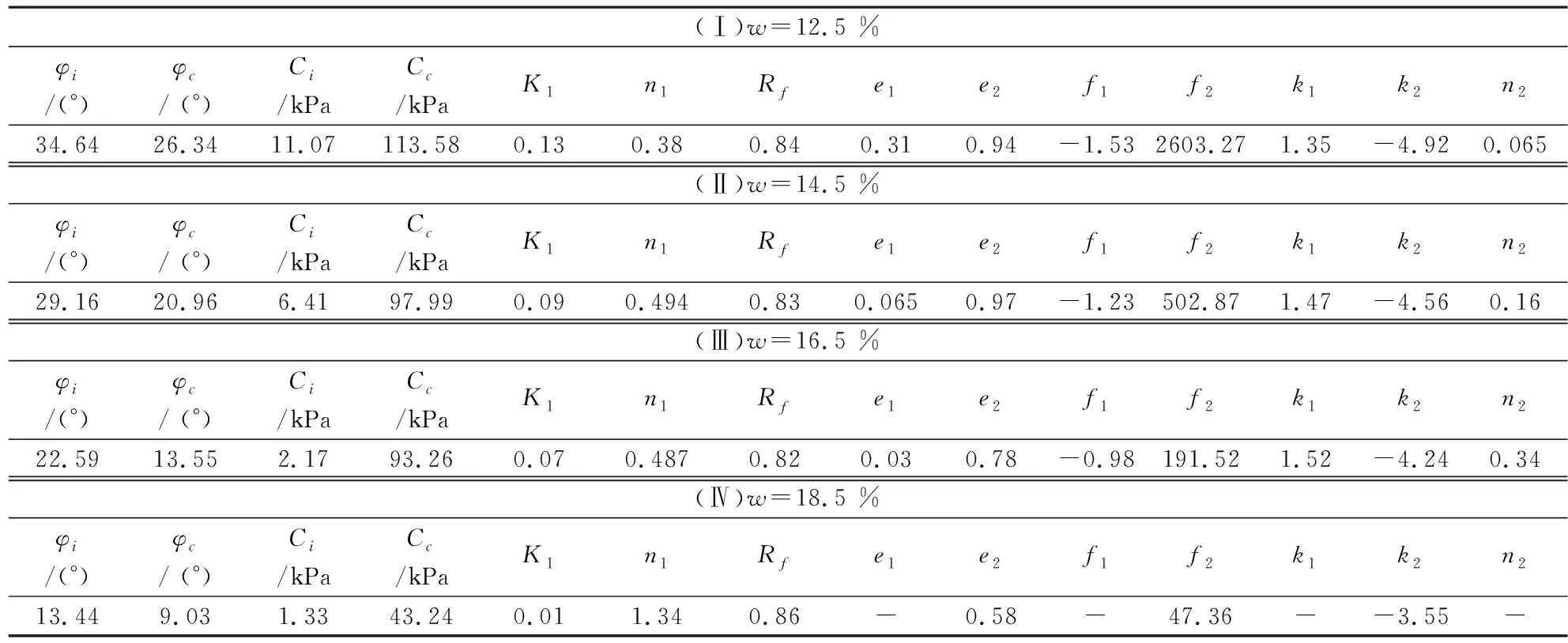
表3 非线性弹性模型参数

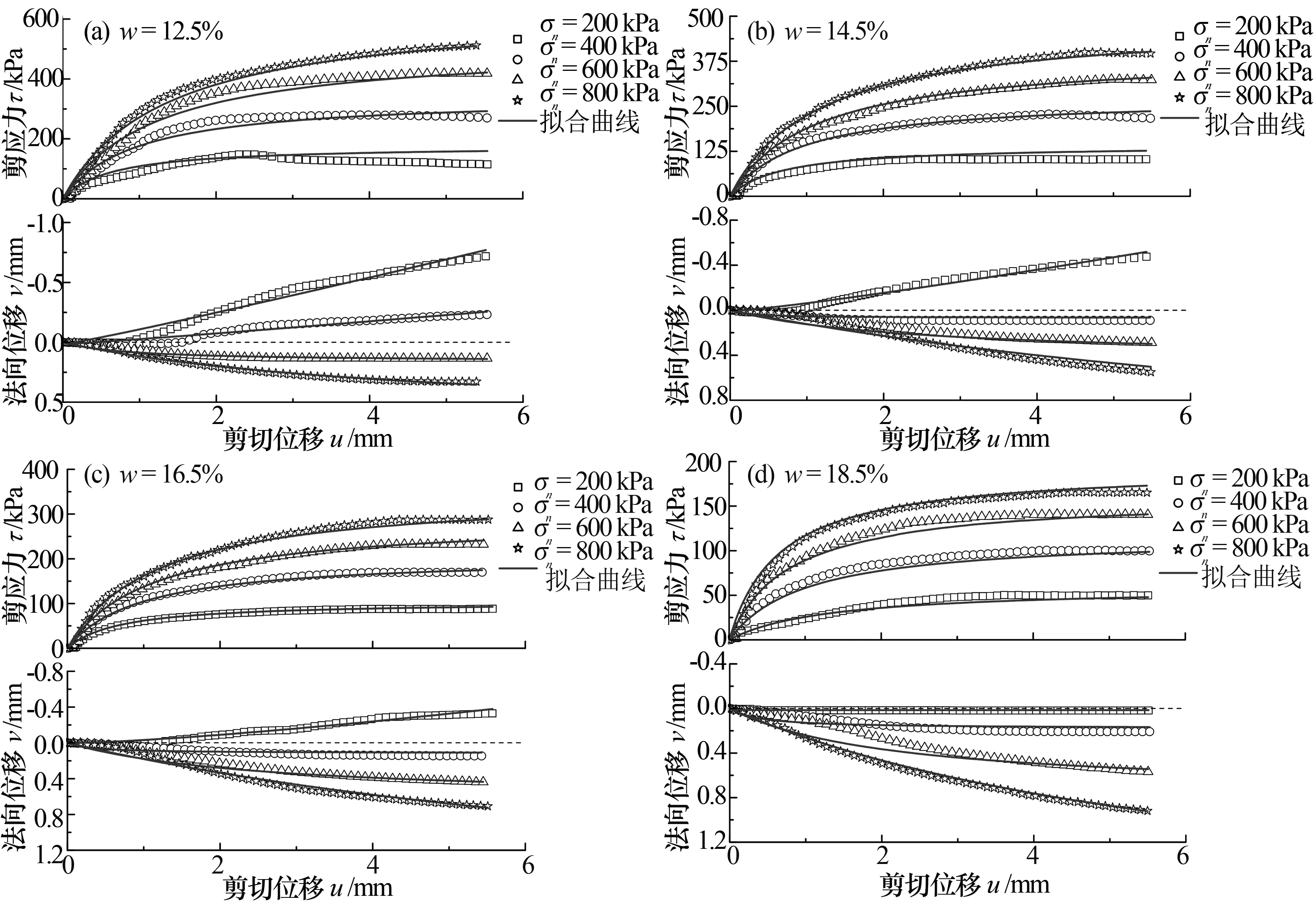
图4 试验结果与模型计算结果的比较

4 模型应用

4.1 LHK心墙堆石坝有限元模拟

对坝体和基岩进行了有限元离散，单元总数为185 949个，结点总数为195 336个。坝体在建模时，在厚度方向将接触黏土层分为3层，接触黏土与混凝土垫层之间预留一层接触面单元，其厚度为接触黏土层厚度的1/10，以模拟两种材料的接触效应。有限元网格划分时，实体单元一般采用8结点六面体等参单元，为适应边界条件以及坝料分区的变化，部分采用三棱体和四面体作为退化的六面体单元处理，单元根据大坝填筑施工顺序排序。整体坐标系定义为：X方向为轴向，指向右岸为正，零点设置在左岸坝顶处；Y方向为顺河向，指向下游为正，零点为轴线0+0.00 m位置；Z方向为垂直向，竖直向上为正，以其高程为坐标值。三维有限元网格剖分如图5所示。

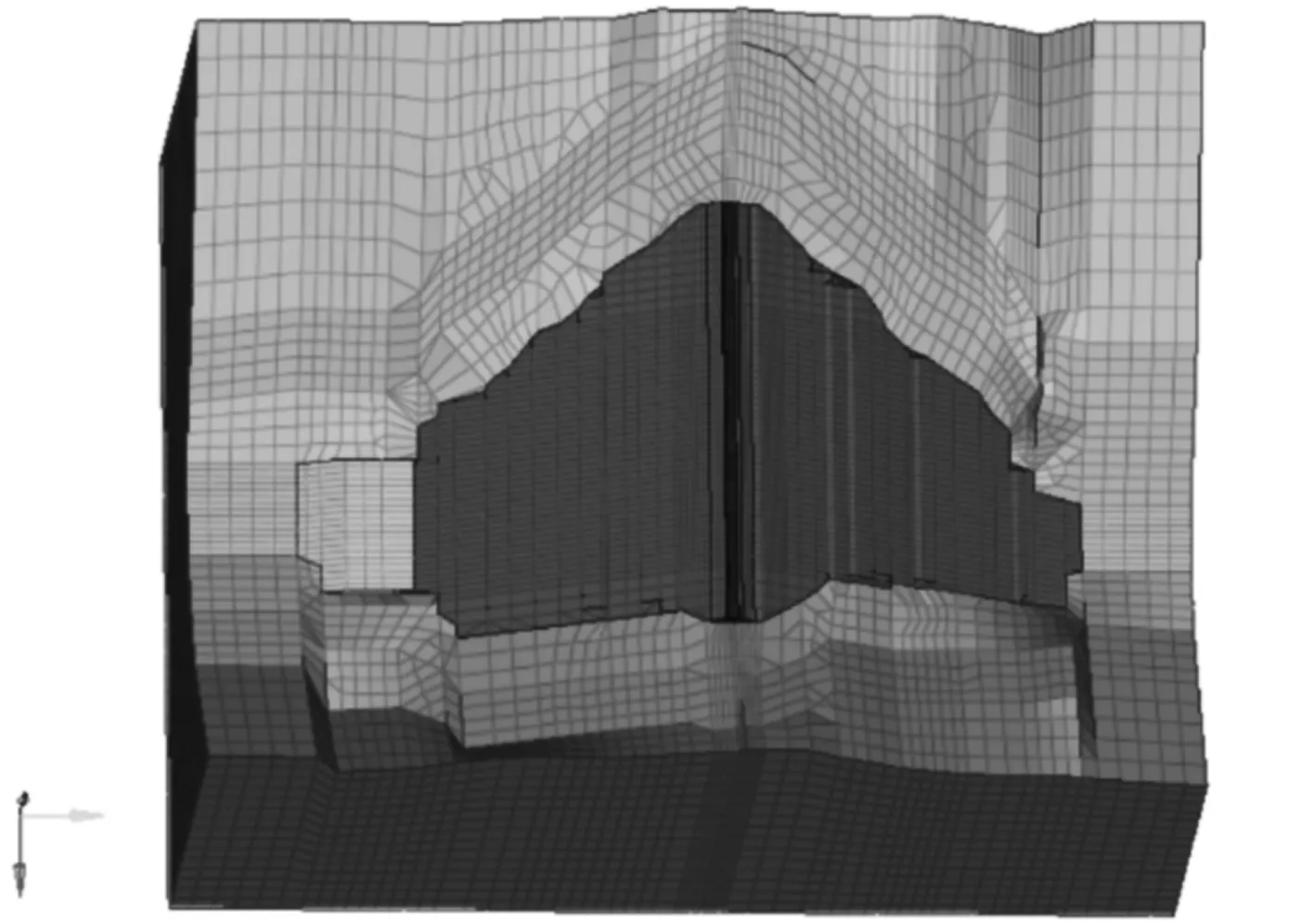
图5 LHK心墙堆石坝三维有限元网格剖分

4.2 模型参数

数值计算全面模拟了坝体的施工填筑、水库蓄水等过程。在堆石坝三维计算中，筑坝料采用邓肯E-B模型计算，结合现场筑坝料检测试验结果和大坝施工前期原型观测资料进行反演，静力计算参数如表4所示。图6为LHK坝0+345.00 m剖面心墙沉降典型测点监测值与反演值对比图，可以看出，反演结果与现场实测值基本能够吻合。

图6 0+345.00m剖面心墙典型测点沉降实测值与反演结果对比

表4 LHK筑坝料静力模型参数

接触黏土的施工含水率为18.5 %，因此接触面模型参数采用表3(Ⅳ)中的参数。

4.3 计算结果

图7给出了采用接触面模型以后的心墙堆石坝坝体沉降以及水平位移等值线图。如图7所示，蓄水期坝体最大沉降为380.31 cm，在水荷载作用下指向下游的最大变形为69.51 cm，指向上游的最大变形为29.06 cm，计算结果符合坝体一般变形规律。

图7 最大横剖面蓄水期坝体变形等值线

图8为蓄水期接触黏土层切向位移分布云图。由图8可知，切向位移沿接触黏土厚度方向自上至下切向位移逐渐减小，切向位移方向均指向河谷，不会出现受拉与混凝土垫层脱空和分离现象。在正常高水位作用下，右坝肩切向位移最大值为85.2 cm，左坝肩切向位移最大值为81.0 cm。计算结果表明，接触黏土层会产生较大的切向变形，因此考虑接触黏土与混凝土垫层接触效应对合理反映高心墙堆石坝的应力变形十分重要。

图8 蓄水期接触黏土层切向位移分布 单位：cm(指向河床为正)

5 结 论

本文研究了LHK心墙堆石坝接触黏土与混凝土垫层接触面的接触特性,通过一系列接触面直剪试验，研究了接触黏土与混凝土之间的剪切特性，并建立了一个可以合理描述接触黏土与混凝土接触面的非线性弹性模型。通过数值模拟分析了接触黏土与混凝土垫层的接触变形特性。形成结论如下:

(1) 含水率和法向应力是影响接触面剪切特性的重要因素，法向应力越低、含水率越高，接触面的抗剪强度越低。随着法向应力和含水率的增加，接触面的法向变形表现出明显的剪缩趋势。

(2) 建立一个非线性弹性模型来描述接触面的力学特性，该模型原理简单，计算便捷，物理意义明确。

(3) 将接触面模型应用于LHK心墙堆石坝三维模型，通过计算分析发现：接触黏土层产生较大切向形变变形，其切向位移沿接触黏土厚度方向自上至下切向位移逐渐减小，切向位移方向均指向河谷，不会出现受拉与混凝土垫层脱空和分离现象。