新型流域雨洪过程模拟方法研究

韩 浩，侯精明，金 钊

(1. 中国科学院地球环境研究所 黄土与第四纪地质国家重点实验室,西安 710061；2. 西安理工大学 省部共建西北旱区生态水利工程国家重点实验室，西安 710048；3. 陕西黄土高原地球关键带国家野外科学观测研究站, 西安 710061)

0 前 言

洪涝灾害是全球所有灾害中发生频率最多的自然灾害[1]。近年来极端降水强度呈增加的趋势变化，极端降水事件风险也呈上升趋势，同时洪涝灾害与极端降水事件是紧密相关的[2]。极端降水事件突发性强、强度大且精确预报难，造成的损失更大。中国洪水灾害问题也十分严重，如近年来受到国内外学者关注的河南省“7·20”极端暴雨事件，此次洪灾造成大规模农作物损坏、房屋倒塌损坏，人员伤亡等[3]。山洪灾害是我国洪涝灾害中最严重的灾种，同时会伴随着一些滑坡和泥石流问题，严重影响社会经济发展[4]。因此，暴雨事件致灾快且损失更加严重，通过研究洪水过程的规律和洪水预报的能力提升，可为洪水灾害风险评估和防洪应对能力的提升有重要的科学和现实应用价值。

目前关于暴雨洪涝灾害的成因分析、洪涝应急管理、洪涝模拟仿真等方面的研究已取得了一定的研究进展[5-7]。数值模拟技术是洪涝灾害模拟的强力技术手段，能系统地实现降雨径流过程的模拟，也能精确地预测洪水的演变过程。目前关于雨洪过程的数值模拟方法，包含物理过程及水文过程机理的数值模型主要有水文模型、水动力模型、水文水动力耦合模型。水文模型不能全面地计算水力特征信息(流速、流量、水位等)，而且很难准确地描绘出水流运动传播的全过程，但水动力模型在模拟具有复杂下垫面的地表产汇流方面具有很大优势[8]。水动力模型主要包括一维、二维、三维水动力模型。二维水动力模型，相比一维模型计算时间长且需要更多的基础资料，但能得到更精确的模拟结果[9]。三维水动力模型需要计算量很大，更是需要进行大量工作完成网格设计和模型校准[10]。二维水动力模型的理论已经很成熟，国内外学者也采用了科学的数值求解方法提高模拟计算精度[11-13]，通过实例验证，二维水动力模型能够满足当前雨洪过程模拟的精度需求。相比传统的水动力模型，耦合水文过程的二维水动力模型具有较高精度和可靠性[4]能准确地预测洪水发生过程的水力特征信息，包括水流速度、流量和水深变化。然而，大多数高效高分辨率雨洪过程数值模型面临模拟计算耗时长的问题，应用GPU并行计算技术为数值模型计算性能的显著提升提供了技术支持。GPU技术主要被国内外学者们用于开展地表径流过程的数值模拟，利用GPU并行计算优势使得高分辨率大规模浅水流动问题的水动力模拟变得可行[14-16]。通过建立基于GPU加速技术的流域雨洪模型能实现雨洪过程的高效高精度模拟已被众多学者所采用，验证结果均表明在模拟精度较高的基础上，通过引入GPU加速技术能极大提升雨洪模型的计算性能[4，7]。然而，国内学者开展GPU并行计算技术的洪水数值模型的研究工作较晚，目前现有单GPU数值模拟方法不能满足大规模、精细化且具有大量计算单元的流域雨洪过程模拟。对于解决单GPU计算性能不足问题，除对数值模型算法进行优化外，可通过引入多GPU并行计算技术，提升模型的计算性能。

本文基于耦合水文过程的二维水动力模型，采用多GPU并行计算技术，提出一种多GPU并行计算的流域雨洪过程模拟方法，量化分析单GPU和多GPU的雨洪过程模拟的计算效率，将多GPU的数值模拟方法实现大尺度流域与洪过程模拟，探讨该方法模拟计算的性能优势，为洪水过程高性能模拟提供技术支撑。

1 研究方法

1.1 二维水动力模型

二维水动力模型的控制方程是二维浅水方程，控制方程的矢量形式可表示为：

(1)

S=Sb+Sf

(2)

公式(1)中:q为qx、qy、h的变量矢量，其中qx、qy分别表示x和y方向的单宽流量，m3/s;h是水深,m；f和g分别为x和y方向的通量矢量；S是源项矢量，包括底坡源项Sb和摩阻源项Sf，方程中不考虑科氏力、风应力等。

控制方程(1)的向量形式如下：

(3)

(4)

公式(3)～(4)中:zb为地形高程,m；h为水深,m，则水位η计算为η=zb+h；u、v分别为x和y方向的流速，m/s,则qx=uh和qy=vh；g是重力系数；Cf是槽底糙率系数，是由曼宁系数n和水深h计算得到：Cf=gn2/h1/3。

模型控制方程中考虑了水文过程，公式(4)中i表示降雨和下渗产生的源项。在计算区域的每个网格计算单元均涉及到降雨量、下渗的计算，开展暴雨雨洪过程的模拟时，可忽略蒸发。

采用Godunov型有限体积格式对控制方程(1)进行离散求解，积分形式如下：

(5)

公式(5)中:Ω为控制单元的有限体积；q为qx、qy、h的变量矢量；f和g分别为x和y方向的通量矢量；S为源项矢量；t为时间变量。

对方程进行离散，则每个网格单元(i,j)在新的时刻更新后的流量可表示为：

(6)

其中

fE=fi+1/2, j

fW=fi-1/2, j

gN=gi, j+1/2

gS=gi, j-1/2

公式(6)中:Δt为时间步长；n是时间步；(i,j)表示网格单元的索引；Δx、Δy分别是结构网格单元在x和y方向的尺寸大小；E、W、N、S分别代表网格单元边界的4个方向；fE、fW、gN、gS分别表示网格单元的界面通量；Si ,j表示网格单元(i,j)在中心的源项。

此外， 采用二阶MUSCL方法对对变量进行空间二阶重构以提高计算精度[14]；基于HLLC近似黎曼求解器计算网格单元界面上的通量[4]；采用龙格-库塔法对时间进行推进[14]；采用底坡通量法对底坡源项进行处理[17]；利用半隐式法计算摩阻源项[7]；通过静水重构解决干湿边界负水深问题[7]。基于以上数值方法，本研究建立了耦合水文过程的二维水动力模型，能实现雨洪过程的稳健数值模拟。

1.2 GPU 并行计算方法

对于文中提出的基于多GPU并行的流域雨洪过程模拟方法，水文及水动力过程的显示格式计算更有利于采用GPU并行计算方法实现高性能模拟计算。对于本研究的计算平台，包括两个GPU，所采用的GPU均是NVIDIA公司的NVIDIA GeForce GTX 1080，CPU是Intel(R) Core (TM)i7-8700。基于多GPU的雨洪过程模拟方法的实现流程如图1所示。主要过程如下：

(1) 对整个研究区域进行计算区域分解，将计算区域分解为与计算平台的GPU个数相同的子计算区域，本研究区域分解为2个子计算区域。

(2) 采用CUDA流方法实现多个GPU进行并行计算，解决多个GPU的数据通信。

(3) 最终将每个GPU中计算的结果数据合并，对结果进行处理分析。

图1 多GPU并行计算流程

1.3 模型计算性能评价

从模型的计算精度和计算效率两个方面对所提出的新型流域雨洪过程模拟方法进行评估。

(1)计算精度分析

本研究所采用的基于单GPU的二维水动力模型已在发表的工作中得到验证[18]，模型具有较高的计算精度。故此处只需对单GPU和多GPU的数值模拟方法的计算精度进行评估，采用相对误差对模拟结果进行比较分析，可采用如下的计算公式：

(7)

公式(7)中:e相对为采用单GPU和多GPU计算的模拟结果数值的相对误差；ν2GPUs是基于多GPU的计算值，ν1GPU是采用单GPU的计算值。

(2)计算效率分析

开展流域雨洪过程模拟方法采用的计算平台包括单GPU和多GPU，所提出的新型流域雨洪过程模拟方法是基于多GPU的，量化比较多GPU较单GPU并行计算的加速计算效率。采用相对加速比对计算效率进行量化分析，公式如下：

(8)

公式(8)中:t1GPU、t1GPUs分别表示数值算法程序在单GPU、两个GPU上运行的时间，s;S相对是相对加速比。

2 结果与分析

2.1 “V”型流域的雨洪过程模拟加速计算效率分析

2.1.1“V”型流域的模拟结果分析

“V”型流域常被国内外学者开展雨洪过程模拟验证分析[4,19]，“V”型流域几何构成如图2所示。流域的坡面和沟道均是不透水的，坡面长、宽、坡度、曼宁系数分别为1 000 m、800 m、0.05、0.015 s/m1/3；沟道长、宽、坡度、曼宁系数分别为1 000 m、20 m、0.02、0.15 s/m1/3。模拟是在均匀降雨条件下进行的，模拟的降雨历时为5 400 s，模拟时长为12 000 s，均匀降雨强度为10.8 mm/h，网格分辨率为5 m。对于边界条件的设置，流域沟道出口处是自由出流的开边界，其他均为闭边界。

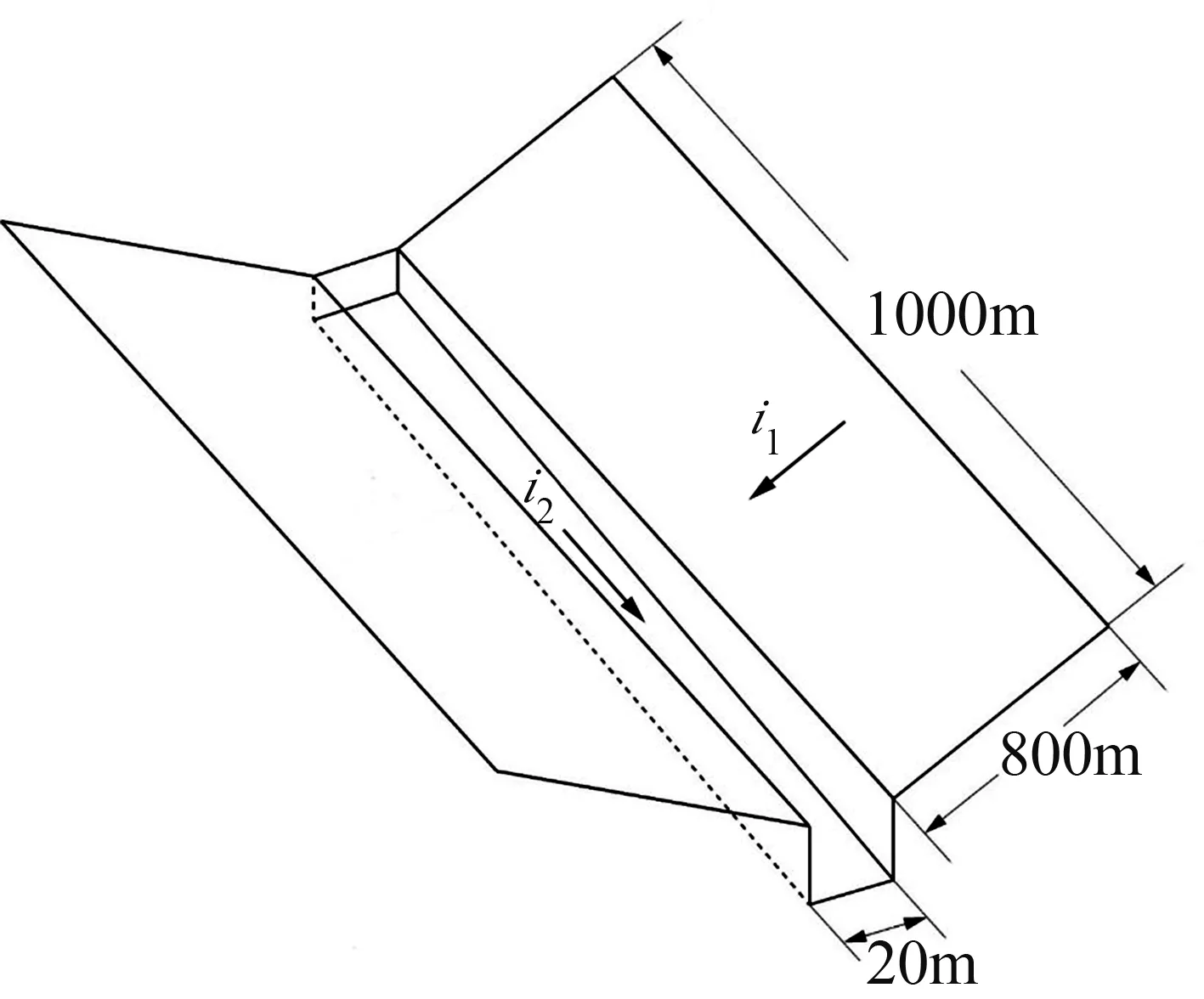
图2 “V”型流域几何构成

如前节所述采用单GPU的雨洪过程模拟方法具有较高的计算精度已在发表的工作中得到验证，故只需进一步验证所提出的基于多GPU的雨洪过程模拟方法的计算精度。建立基于单GPU和多GPU的数值模型开展雨洪过程模拟，将多GPU和单GPU计算的水深结果进行比较分析，单GPU和多GPU模拟的水深分布值(t=3 600 s)如图3所示。由图3可知，两种情景下的水深分布值相同；通过计算单GPU和多GPU的“V”型流域雨洪过程模拟水深值的相对误差，计算得到相对误差为0，结果表明多GPU的模拟方法具有较高的计算精度。综上分析，基于多GPU的雨洪过程模拟方法是可行且可靠的。

图3 单GPU和多GPU的雨洪过程模拟计算结果对比

2.1.2雨洪过程模拟的加速计算效率分析

“V”型流域为5 m地形分辨率时，网格数为6.48×104。由于网格较少，不能较好地反映所提出模拟方法的加速计算性能优势。在参数设置保持不变的基础上，开展地形分辨率为1 m(网格数为1.62×106)、2 m(网格数为4.05×105)的“V”型流域的雨洪过程模拟。如表1所示，量化分析了两种网格数工况下的多GPU计算较单GPU的相对加速比，加速比分别为1.57、1.27倍，表明所提出的方法具有明显的加速计算效果。通过比较分析，计算单元的网格数越多，相对加速比越大，加速效率越高。在计算区域具有较多网格数的情形时，采用多GPU并行计算的雨洪过程模拟方法的加速计算效率越显著。因此，所提出的流域雨洪过程模拟方法具有显著的加速计算性能。

表1 “V”型流域雨洪过程模拟的计算效率结果

2.2 葫芦河流域雨洪过程模拟加速计算效率分析

2.2.1葫芦河流域概况

葫芦河流域位于我国黄土高原地区，是渭河上游最大的支流，位于东经105°05′～106°30′、北纬 34°30′～36°30′，面积约为1.07×104km2，区域地形如图4所示。流域的北部和东部是六盘山山脉，南部是秦岭山脉，西部是黄土高原[20]。葫芦河流域年平均日照时数约2 300 h，年总太阳辐射量为544.284 kJ/cm2[21]。流域干流建有秦安和静宁水文站，多年平均降水量为440.2 mm。

图4 研究区域

2.2.2模型基础参数

建立基于多GPU的葫芦河流域雨洪过程数值模型，模型输入的基础参数包括地形数据、降雨数据、曼宁系数等。地形分辨率为30 m的地形数据来源地理空间数据云(http://www.gscloud.cn)，流域的计算网格数约为2.2×107。降雨数据采用设计暴雨，选用50年一遇的设计暴雨，降雨历时为2 h，累积降雨量约为54 mm，采用平凉市暴雨强度公式，计算公式如下[22]：

(9)

公式(9)中:i为设计降雨强度，mm/min；P是重现期，a；t为降雨历时，min。

为了量化所提出的模拟方法在开展大尺度流域雨洪过程模拟的加速计算性能，故对其他参数进行概化处理，曼宁系数参考经验值取值，河流区域的曼宁系数为0.033，其他区域的曼宁系数为0.06。由于是在场次暴雨条件下进行模拟计算，忽略蒸发，设置河道以外区域的下渗为0 mm。

2.2.3模拟加速计算效率分析

采用多GPU并行计算的雨洪过程模拟方法，建立基于多GPU的葫芦河流域雨洪过程数值模型，模拟重现期为50年的设计暴雨(2 h)条件下的葫芦河流域雨洪过程。模拟总历时为5 h，其中降水过程和退水过程为2 h和3 h。由表2所示，统计了在不同计算平台上模型运行时间，显然在当前设备条件下，由于网格数较多，内存受限，基于单GPU的数值模型没有完成计算过程；但所提出的多GPU模拟方法完成了葫芦河流域的的雨洪过程模拟计算。由表2可见，基于多GPU的模拟计算时间为1.8 h，相对于设计模拟时间(5 h)的加速比约为2.8倍，表明多GPU并行计算能实现大尺度流域的雨洪过程模拟。因此，所提出的基于多GPU的数值模拟方法可满足较大尺度流域雨洪过程模拟的需求。同时，该方法具有模拟精度高和计算效率快的优势，可拓展到城市洪涝过程的高性能模拟。

表2 模拟计算效率结果

3 结 论

本研究基于耦合水文过程的二维水动力模型，引入多GPU并行计算技术，提出了一种基于多GPU并行的新型流域雨洪过程模拟方法，采用典型算例和实际算例对所采用的模拟方法进行了验证和计算效率量化分析，形成结论如下：

(1) 模拟“V”型流域的雨洪过程中，通过比较分析基于单GPU和多GPU并行计算的模拟水深结果，表明多GPU雨洪过程模拟方法可靠可信；在量化分析地形分辨率为1(网格数为1.62×106)、2m(网格数为4.05×105)情景下，多GPU计算和单GPU的相对加速比分别为1.57、1.27倍，多GPU模拟方法计算优势明显优于单GPU。

(2) 建立基于多GPU的葫芦河流域雨洪过程数值模型，量化分析葫芦河流域雨洪过程模拟的加速计算效率，结果表明所提出的方法能实现大尺度葫芦河流域雨洪过程的高性能模拟。